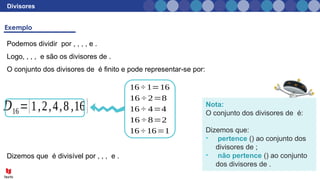
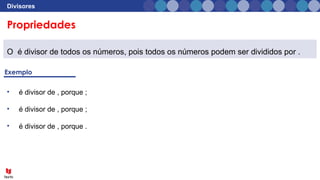
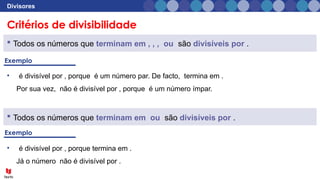
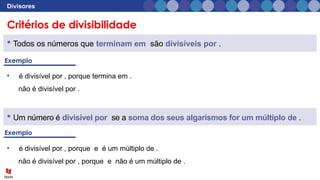
O documento aborda o conceito de divisores em matemática, explicando que divisores são números pelos quais um número pode ser dividido sem deixar resto. Ele apresenta exemplos de divisores e critérios de divisibilidade, como regras para identificar se um número é divisível por 2, 3, 5, entre outros. Além disso, inclui exercícios práticos para aplicar o conhecimento sobre divisores.

1. Matemática | 5.º Ano
Divisores

2. Divisores
Quando conseguimos fazer uma divisão inteira e o resto é zero, o número pelo qual
dividimos é um divisor.
Podemos dividir por , , , , e .
Logo, , , , , e são os divisores de .
O conjunto dos divisores de é finito e pode representar-se por: 12 ÷1=12
12 ÷ 2=6
12 ÷ 3=4
12 ÷ 4=3
12 ÷ 6=2
12 ÷12=1
𝐷12={1,2,3,4,6,12}
Dizemos que é divisível por , , , , e .

3. Divisores
Podemos dividir por , , , , e .
Logo, , , , e são os divisores de .
O conjunto dos divisores de é finito e pode representar-se por:
16 ÷ 1=16
16 ÷ 2=8
16 ÷ 4=4
16 ÷ 8=2
16 ÷ 16=1
Nota:
O conjunto dos divisores de é:
Dizemos que:
• pertence () ao conjunto dos
divisores de ;
• não pertence () ao conjunto
dos divisores de .
𝐷16={1,2,4,8,16}
Dizemos que é divisível por , , , e .

4. Divisores
Todo o número natural maior do que tem vários divisores.
• é divisor de , porque ;
• é divisor de , porque ;
• é divisor de , porque .
Qualquer número diferente de zero é divisor de si próprio, porque, ao ser dividido por
si próprio, obtém-se o resultado .
Propriedades

5. Propriedades
Divisores
O é divisor de todos os números, pois todos os números podem ser divididos por .
• é divisor de , porque ;
• é divisor de , porque ;
• é divisor de , porque .

6. Divisores
O é o menor divisor de qualquer número e o próprio número é o maior divisor.
Podemos dividir por , , , , e .
O conjunto dos divisores de pode representar-se por:
18 ÷ 1=18
18 ÷ 2=9
18 ÷ 3=6
18 ÷ 6=3
18 ÷ 9=2
𝐷18 ={1 , 2 ,3 ,6 , 9 ,16 }
18 ÷ 18=1
Nos divisores de , o é o menor divisor e o é o maior divisor.
Por essa razão, o conjunto dos divisores de um número é finito.

7. Critérios de divisibilidade
Divisores
 Todos os números que terminam em , , , ou são divisíveis por .
• é divisível por , porque é um número par. De facto, termina em .
Por sua vez, não é divisível por , porque é um número ímpar.
• é divisível por , porque termina em .
Já o número não é divisível por .
 Todos os números que terminam em ou são divisíveis por .

8. Critérios de divisibilidade
Divisores
 Todos os números que terminam em são divisíveis por .
 Um número é divisível por se a soma dos seus algarismos for um múltiplo de .
• é divisível por , porque termina em .
não é divisível por .
• é divisível por , porque e é um múltiplo de .
não é divisível por , porque e não é um múltiplo de .

9. Critérios de divisibilidade
Divisores
 Todos os números que terminam em , , , ou são divisíveis por .
 Todos os números que terminam em são divisíveis por .
 Um número é divisível por se a soma dos seus algarismos for um múltiplo de .
• é divisível por , porque e é um múltiplo de .
 Todos os números que terminam em ou são divisíveis por .

10. Exercício 1
Divisores
Indica todos os números naturais que sejam simultaneamente divisores de e de .
Resolução:
Os números naturais , , e são divisores de e de ,
em simultâneo.
𝐷36={1 , 2 , 3 , 4 , 6 , 9 , 12 , 18 , 36 }
𝐷42={1 , 2 , 3 , 6 , 7 , 14 , 21 , 42}
36 ÷ 1=36
36 ÷ 2=18
36 ÷ 3=12
36 ÷ 4=9
36 ÷ 6=6
36 ÷ 9=4
36 ÷ 12=3
36 ÷ 18=2
36 ÷ 3 6=1
42÷ 1=42
42÷ 2=21
42÷ 3=14
42÷ 6=7
42÷ 7=6
42÷ 14=3
42÷ 21=2
42÷ 42=1

11. Exercício 2
Divisores
De um número com quatro algarismos, , desconhece-se o algarismo das unidades.
Descobre de modo a obteres um número de quatro algarismos que seja divisível:
) por ; ) por ; ) por ; ) por e , em simultâneo.
Resolução:
) Para o número ser divisível por , o algarismo das unidades terá de ser , , , ou .
, , , ou
) Para o número ser divisível por , o algarismo das unidades terá de ser ou .
ou

12. Exercício 2
Divisores
De um número com quatro algarismos, , desconhece-se o algarismo das unidades.
Descobre de modo a obteres um número de quatro algarismos que seja divisível:
) por ; ) por ; ) por ; ) por e , em simultâneo.
Resolução (continuação):
)
Assim, o algarismo das unidades poderá ser , ou , obtendo-se assim as somas , e ,
respetivamente, que são números múltiplos de .
, ou

13. Exercício 2
Divisores
De um número com quatro algarismos, , desconhece-se o algarismo das unidades.
Descobre de modo a obteres um número de quatro algarismos que seja divisível:
) por ; ) por ; ) por ; ) por e , em simultâneo.
Resolução (continuação):
) Para o número ser divisível por , o algarismo das unidades terá de ser , , , ou .
Por outro lado, para ser divisível por , o algarismo das unidades terá de ser ou .
Assim, para o número ser divisível simultaneamente por e por , o algarismo das unidades
terá de ser .