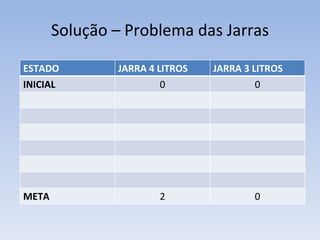
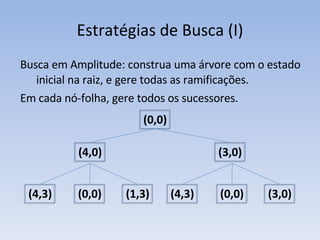
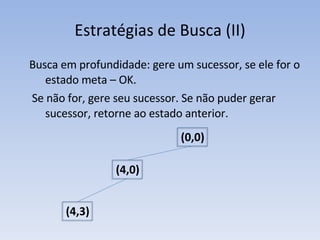
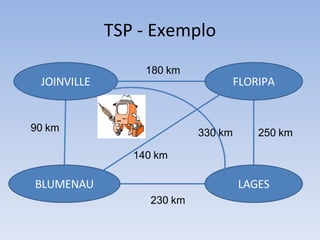
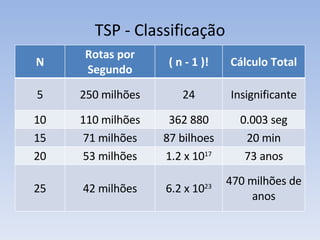
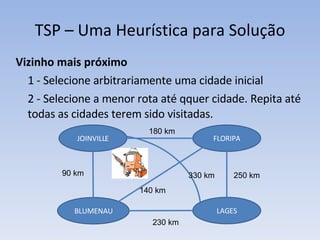
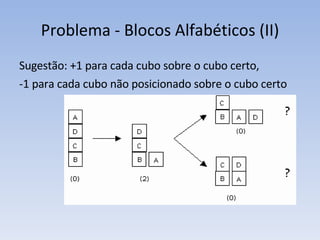
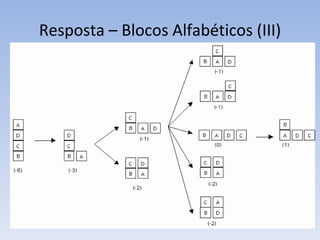
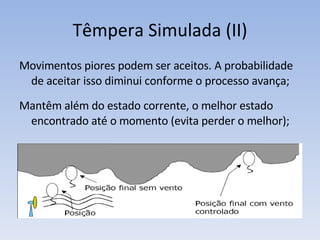
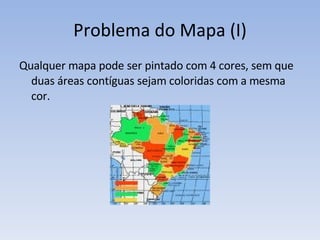
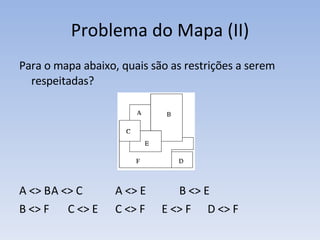
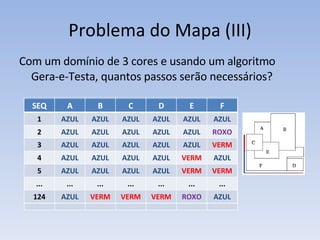
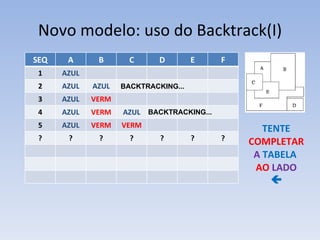
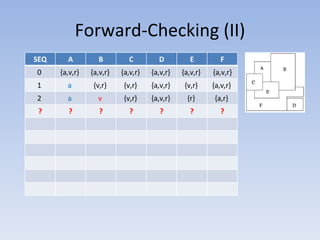
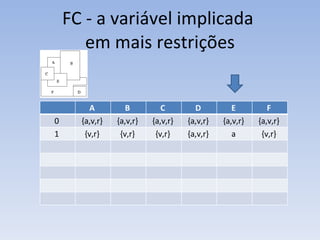
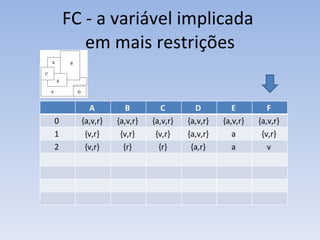
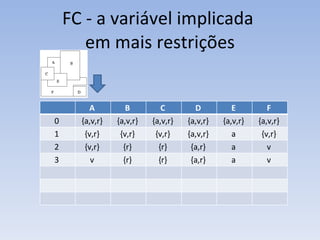
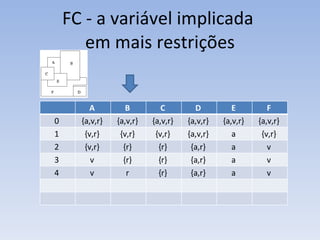
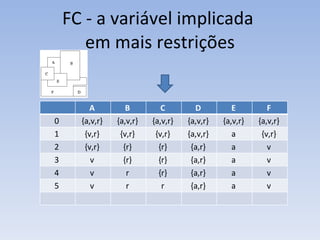
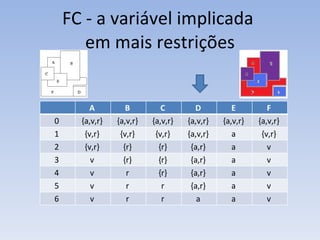
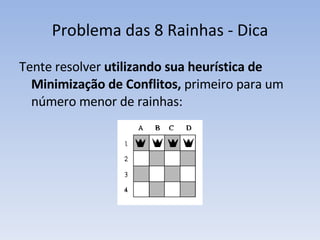
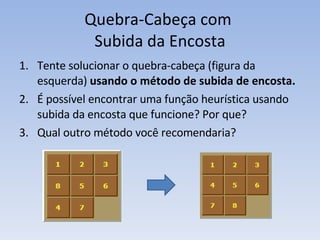
O documento discute vários problemas e estratégias de inteligência artificial, incluindo o problema das jarras, busca em profundidade e amplitude, heurísticas como subida da encosta e vizinho mais próximo, e satisfação de restrições em problemas de coloração de mapas.
![I nteligência Artificial Problemas e Heurísticas (versão final) Rafael Rosario [email_address] [email_address]](https://image.slidesharecdn.com/iaproblemasheuristicasv31comrespostas-1207228346828336-8/75/IA-Problemas-Heuristicas-1-2048.jpg)