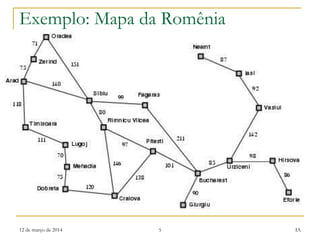
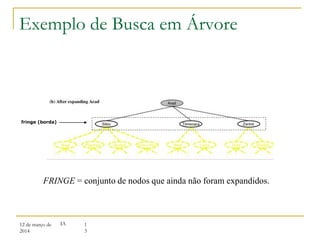
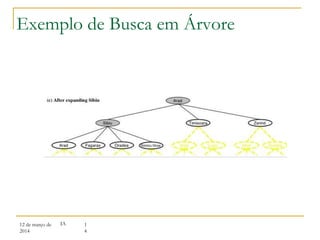
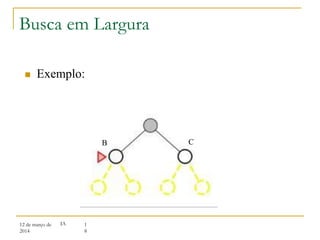
O documento discute algoritmos de busca para resolução de problemas, apresentando:
1) Tipos de problemas que podem ser abordados via busca, como estados únicos e informação parcial;
2) Formulação do problema de busca, definindo estado inicial, função sucessora e teste de meta;
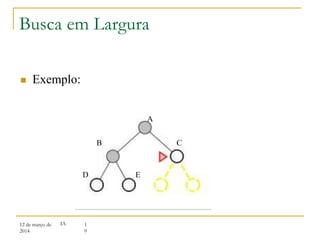
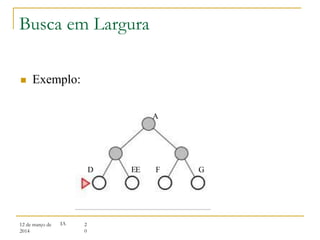
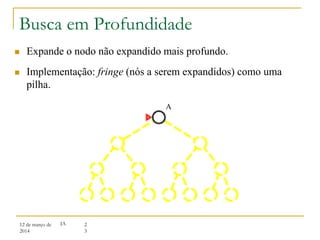
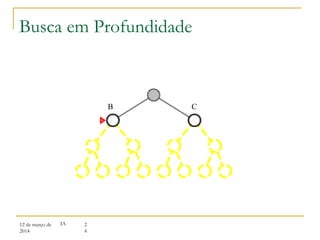
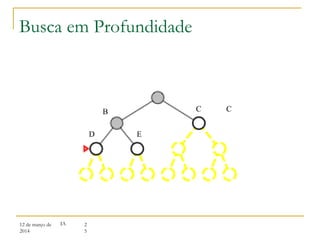
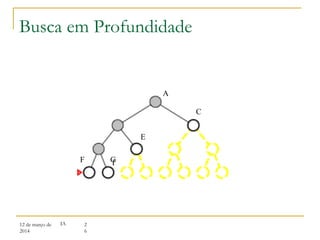
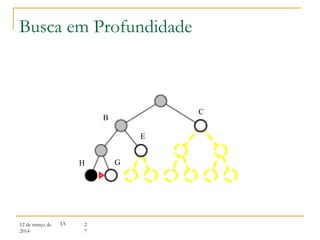
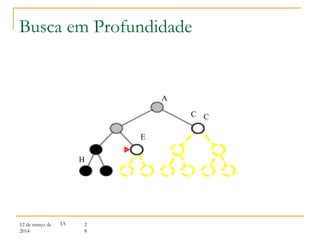
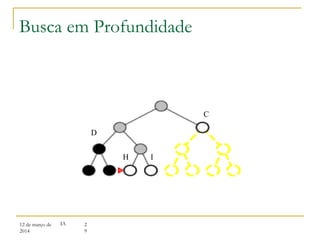
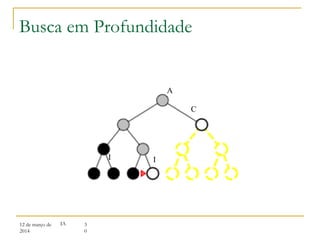
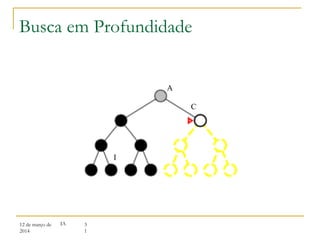
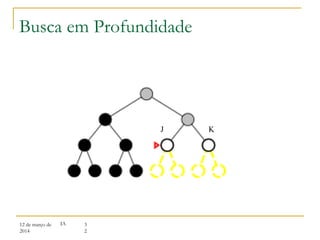
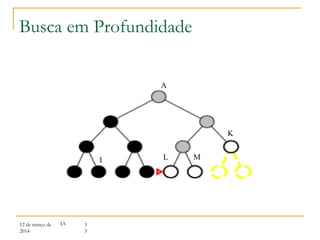
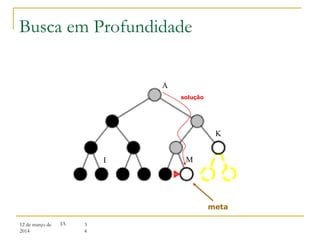
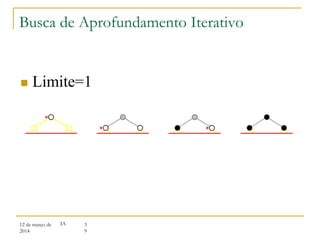
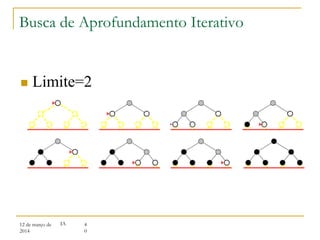
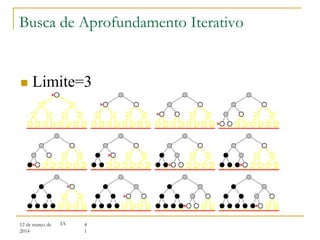
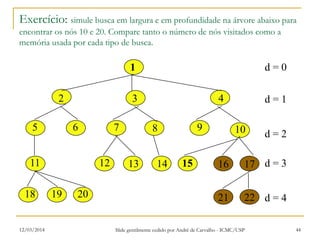
3) Algoritmos de busca não informada como busca em largura, profundidade e aprofundamento iterativo.