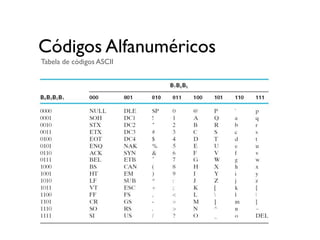
1) O documento descreve a história dos computadores desde o ábaco chinês até os computadores modernos, com marcos como Babbage, Turing, ENIAC e gerações de hardware. 2) Inclui detalhes sobre representação da informação em binário e sistemas de numeração como binário, hexadecimal e ASCII. 3) Discutem operações aritméticas básicas em sistemas binários.

1. História dos
Computadores
Arquitetura de Computadores
Prof Evandro Manara Miletto
IFRS - Campus Porto Alegre
INSTITUTO FEDERAL
Campus Porto Alegre
RIO GRANDE DO SUL

2. Sumário
Introdução
Breve historia dos computadores
Representação da informação
Sistemas de numeração:
conversão entre bases
representação de números
operações aritméticas
Códigos alfanuméricos

3. Programa
Sistemas Digitais
Representação da informação
Álgebra de Boole
Circuitos combinatórios
Circuitos sequenciais
Máquinas de estado
Arquitetura de Computadores
Memória, Processador e Barramentos
Linguagem Máquina

4. MARCOS HISTÓRICOS

5. A primeira calculadora que
se tem notícias é o Ábaco,
de origem chinesa, do
séculoV a.C. capaz de
efetuar operações
algébricas elementares.
Anteriormente à década
de 40 já existiam
calculadoras mecânicas -
destaque para a máquina
das diferenças do britânico
Charles Babbage

6. Atribui-se ao francês Blaise Pascal
(1623-1662) construiu a primeira
calculadora mecânica capaz de
fazer somas e subtrações.
Durante muitos anos nada se soube sobre
essa máquina, por isso, atribuía-se a Blaise
Pascal a autoria da primeira máquina
calculadora
Entretanto, Wilhelm Schickard (1592-1635) foi
quem construiu a primeira máquina de
calcular: somar, subtrair, multiplicar e dividir;
perdida durante a guerra dos trinta anos;

7. Em 1801, Joseph Marie Jacquard
inventou um tear programável
mecânico dotado de uma leitora de
cartões perfurados , os quais
representavam os desenhos do tecido;
Um processador das informações
relativas à padronagem do tecido;
Devido ao seu eficiente
funcionamento o tear foi
considerado o primeiro
exemplo prático de
desemprego provocado pela
automação.

8. Charles Babbage (1792-1871)
Computador Analítico em 1822
dispositivo chamado de Moinho
(uma máquina de somar com precisão de
até 50 casas decimais),
um dispositivo de entrada (inspirado no tear
de Jacquard) para ler cartões perfurados
com números (os dados) e também
instruções (o que fazer com os dados).
Ainda, um dispositivo de memória que
chamou de ARMAZÉM (guardar os
números) um banco com 1000
registradores (cada qual capaz de
armazenar um número de 50 dígitos)
e um dispositivo impressor para dar
saída aos resultados.

9. Instruções (gravadas em cartões) implementadas pelo moinho:
entrar com um número no armazém
entrar com um número no moinho
mover um número do moinho para o armazém
mover um número do armazém para o moinho
comandar o moinho para executar uma operação
sair com um resultado.
Babbage contou com a colaboração da matemática Ada
Augusta Byron, Lady Lovelace, filha do poeta Lord
Byron.Ada desenvolveu séries de instruções para o
calculador analítico, criando conceitos como sub-
rotinas, loops e saltos condicionais.
Babbage é considerado o precursor do computador.
Ada é considerada a precursora do software.

10. Herman Hollerith (1860-1929)
também inspirou-se nos cartões de
Jacquard para criar uma máquina para
acumular e classificar informações -
a Tabuladora de Censo.
(processamento dos dados do censo)
1941- Konrad Zuse
(Alemanha) Primeiro
computador digital,
automático, programável, de
propósito geral,
completamente funcional
(eletromecânico).

11. Colossus, desenvolvido na Inglaterra no
período de 1939 a 1943 com a intenção de
quebrar o código da máquina de criptografia
alemã denominada Enigma, que gerava
seqüências aleatórias com período de 1019
caracteres.
Participação de Alan Turing.
Teoria Matemática da Computação
Algorítimo: como a representação
formal e seistemática de um processo
Um problema terá solução
algorítimica se existir uma Máquina de
Turing para representá-lo.

12. 1944 - Howard Aiken (Universidade de Harvard - EUA)
Primeiro computador eletromecânico automático de
grande porte.

13. Computadores
1ª geração -Válvulas (1945 – 1955)
2ª geração - Transistores (1955 – 1965)
3ª geração - CI (1965 – 1980)
Quarta geração (1980 em diante)
VLSI (Very Large Scale Integration)
Evolução Histórica

14. 5
Resmo dos marcos históricos e outros...
1642 – Calculadora mecânica - Pascal
1834 – Máquina analítica – Babbage
1943 – COLOSSUS – 1º Computador eletrônico
1964 – IBM 360 – 1ª linha de produtos
1974 – Intel 8080 – 1º chip de 8 bits para uso geral
1981 – IBM PC – 1º PC tal como os conhecemos
1987 – Sun SPARC – 1ª Workstation RISC

15. GERAÇÕES

16. ENIAC (Eletronic Numerical Integrator and Calculator)
Desenvolvido pelo exército americano para cálculo balístico
1ª Geração (1945 – 1955)
Soma de 2 nos em 0,0002 s
Multiplicação em 0,0003 s
111 m3, 30 ton,
17000 válvulas a vácuo,
50000 comutadores,
70000 resistências,
7500 interruptores
Consumo:
100000 a 20000 Watts

17. IBM 1401
marco inicial: surgimento dos transistores.
Máquinas diminuem o tamanho.Aplicações passam além da
científica e militar para administrativa e gerencial
2ª Geração (1955 – 1965)
Surgem as primeiras
linguagens de programação.
Surgimento dos núcleos de
ferrite, fitas e tambores
magnéticos usados como
memória.

18. DEC PDP-11
3ª Geração (1964 – 1971)
IBM 360
Marco inicial: surgimento dos Circuitos Integrados (C.I.).
Evolução dos Sistemas Operacionais, surgimento da multi-
programação, real time e modo interativo.A memória é feita
de semicondutores e discos magnéticos.

19. 4ª Geração (1971 - 1981)
Marco inicial: surgimento do microprocessador e LSI,
grande redução no tamanho dos computadores. Surgem
muitas liguagens de alto-nível e nasce a teleinformática,
transmissão de dados entre computadores através de rede

20. 5ª Geração (1981 - atual )
Surgimento do VLSI. Inteligência artificial,Altíssima velocidade
de processamento, alto grau de interatividade, etc.
Supercomputadores
Automação comercial e industrial
CAD/CAM e CAE
Robótica
Computação ubíqua
Computação móvel
Era on-line (comunicação Web)

21. REPRESENTAÇÃO DA INFORMAÇÃO

22. Representação da Informação
Nos computadores, a informação é representada por sinais
elétricos:
Tensão alta – ex. 3 a 5.5V – HIGH - 1(um)
Tensão baixa – ex. -0.5 a 2V – LOW - 0 (zero)
Os circuitos de um
computador trabalham
com sinais binários,
representados por níveis
de tensão
0
2
3
5
volts
tempo
nível lógico 0
transição
nível lógico 1Bit 1 (um)
Bit 0 (zero)

23. SISTEMAS DE NUMÉRICOS

24. Utiliza 10 símbolos 0,1,2,3,4,5,6,7,8,9
Cada posição tem um valor intrínseco que equivale a 10 vezes o
valor da posição que está a sua direita.
Ex: 327
3x102 + 2x101 + 7x100 = 327
Sistemas Decimal (base 10)
centena dezena unidade
102 101 100 base
3 2 7 dígitos

25. Sistemas de Numeração
Decimal (base 10) - 10 dígitos - 0 a 9
562.3 = 5×102 + 6×101 + 2×100 + 3×10-1
Binário (base 2) - 2 dígitos - 0 e 1
10110.01 = 1×24 + 0×23 + 1×22 + 1×21 + 0×20 + 0×2-1 + 1×2-2 = (22.25)10
Potências de 2
K (Kilo) - 210
M (Mega) - 220
G (Giga) - 230
T (Tera) - 240

26. 13
Conversão base 10 ⇒ base 2
Subtrai-se sucessivamente a maior potência de 2 possível
Ex: (41)10
(41)10 = (101001)2
25 = 32 41 - 32 = 9
23 = 8 9 - 8 = 1
20 = 1 1-1 = 0
41
+
Sistemas de Numeração

27. Conversão base 10 ⇒ base 2 (outro método)
Divide-se sucessivamente por 2 e anota-se o resto
Ex: (41)10
(41)10 = (101001)2
Sistemas de Numeração
Divisão inteira Resto
41 ÷ 2 = 20 1
20 ÷ 2 = 10 0
10 ÷ 2 = 5 0
5 ÷ 2 = 2 1
2 ÷ 2 = 1 0
1 ÷ 2 = 0 1
Bit + significativo
Bit - significativo

28. Hexadecimal (base 16) e Octal (base 8)
Representação fácil de quantidades binárias
Octal: 8 dígitos - 0 a 7
Hexadecimal: 16 dígitos - 0 a 9;A a F
Exemplos:
(25)8 = 2×81 + 5×80 = (21)10
(B3)16 = 11×161 + 3×160 = (179)10
Sistemas de Numeração

29. Decimal Binário Octal Hexadecimal
0 0000 00 0
1 0001 01 1
2 0010 02 2
3 0011 03 3
4 0100 04 4
5 0101 05 5
6 0110 06 6
7 0111 07 7
8 1000 10 8
9 1001 11 9
10 1010 12 A
11 1011 13 B
12 1100 14 C
13 1101 15 D
14 1110 16 E
15 1111 17 F
Sistemas de Numeração
Tabela de conversão de Bases
Decimal (Base 10): 0 a 9
Binária (Base 2): 0 e 1
Hexadecimal (Base 16): 0 a F
Octal (Base 8): 0 a 7

30. Conversão base 2 ⇒ base 8 (Grupos de 3 bits)
(101001)2 = (51)8
Conversão base 2 ⇒ base 16 (Grupos de 4 bits)
(101001)2 = (29)16
Sistemas de Numeração
Tabela de conversão de Bases
Divide-se o número em grupos de quatro bits, a
partir da direita, substituindo-se tais grupos pelos
símbolos hexadecimais correspondentes.
101 001
5 1
0001 1001
2 9

31. Números inteiros
Armazenamento dependente do hardware
8 bits (byte): [0; 255] ou [-128; 127]
16 bits (word): [0; 65535] ou [-32768; 32767]
32 bits (double word): [0; 4294967295]
ou [-2147483648; 2147483647]
64 bits .......
Números fraccionários
Representados na forma ± mantissa × 10 ± expoente
Números inteiros e fracionários

32. Mesmas regras da base 10
Adição
Subtração
10110 transporte
10110 parcela 1
+10011 parcela 2
101001 soma
0011 transporte
10110 diminuendo
-10011 diminuidor
00011 diferença
Operações Aritméticas

33. Mesmas regras da base 10
Multiplicação
Operações Aritméticas
1101 multiplicando
×101 multiplicador
1101
0000
1101
1000001 produto

34. ASCII - American Standard Code for Information Interchange
7 bits + 1 de paridade (opcional) = 128 caracteres
Pequeno conjunto de caracteres
Caracteres de controle
Sinais ortográficos
Algarismos
Letras maiúsculas e minúsculas (A...Z; a...z)
Sinais algébricos
Códigos Alfanuméricos
ASCII extendido - 8 bits = 256 caracteres

35. Códigos Alfanuméricos
Tabela de códigos ASCII

36. 23
Códigos Alfanuméricos
UNICODE
16 bits
ISO / IEC 10646
Grafismos de todo o mundo
Alfabeto latino
Alfabeto cirílico
Caracteres chineses, etc.
Necessita conversão little-endian big-endian
Little-endian - byte de maior peso à esquerda
Big-endian - byte de maior peso à direita

37. WEBER, R. F. ; Fundamentos de Arquitetura de Computadores
TANENBAUM,A. S.; Organização Estruturada de Computadores.
Wikipedia; http://pt.wikipedia.org/wiki/Porta_lógica
bibliografia

38. contato
Prof Evandro Manara Miletto
IFRS Campus Porto Alegre
Rua Ramiro Barcelos, 2777 - Bairro Santana
Fone (51) 3308-5148
evandro.miletto@poa.ifrs.edu.br
http://www.poa.ifrs.edu.br/
INSTITUTO FEDERAL
Campus Porto Alegre
RIO GRANDE DO SUL