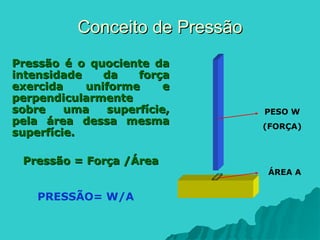
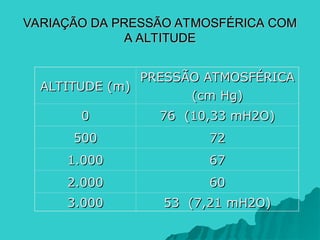
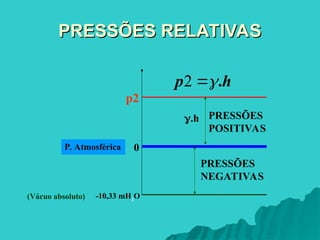
O documento aborda os princípios da hidrostática, focando na pressão em líquidos e sólidos e na variação da pressão com a profundidade. Explora a lei de Stevin, que estabelece que a diferença de pressão em um líquido em equilíbrio é proporcional à diferença de profundidade, e descreve a pressão atmosférica e sua variação com a altitude. Além disso, menciona a experiência de Torricelli que determina o valor da pressão atmosférica normal.