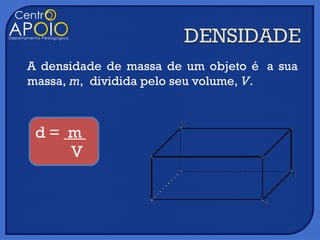
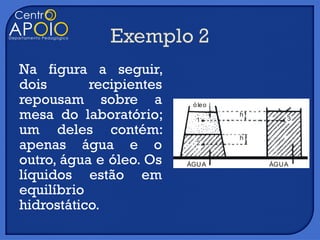
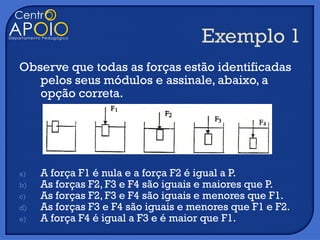
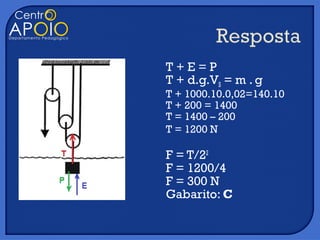
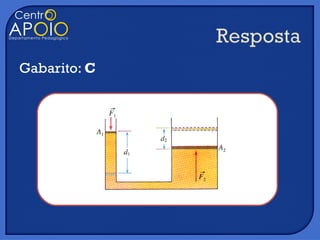
O documento discute três tópicos: 1) a definição de densidade de massa como a massa dividida pelo volume de um objeto, 2) a lei de Stevin sobre a variação da pressão em um fluido sob a ação da gravidade, 3) o uso histórico de sinos metálicos para recuperar objetos do fundo do mar.

2. A densidade de massa de um objeto é a sua
massa, m, dividida pelo seu volume, V.
d= m
V

3. Lei de Stevin
Consentiu em calcular a diferença da pressão
existente entre dois pontos de certo fluído
homogêneo que está tanto em equilíbrio como
sob a ação da gravidade.
p = p0 + dgh

4. Há séculos atrás, grandes sinos
metálicos eram usados para se
recuperar objetos de artilharia no
fundo do mar. O sino era introduzido
na água, com uma pessoa em seu
interior, de tal modo que o ar contido
nele não escapasse à medida que o
sino afundasse, como indica a figura a
seguir.

5. Supondo que no
instante focalizado na D
ar
figura a água se
encontre em equilíbrio água
hidrostático, compare
as pressões nos pontos ar A C
A, B, C e D usando os B
símbolos de ordem >
(maior), = (igual) e <
(menor). Justifique sua
resposta.

6. PA = PB > PC > PD
ar
D
água
ar A C
B

7. Na figura a seguir,
dois recipientes
repousam sobre a
mesa do laboratório;
um deles contém:
apenas água e o
outro, água e óleo. Os
líquidos estão em
equilíbrio
hidrostático.

8. Sobre as pressões hidrostáticas P1, P2 e P3,
respectivamente, nos pontos 1, 2 e 3 da figura, pode–se
afirmar corretamente que:
a) P1 = P3 > P2 d) P2 > P3 > P1
b)P2 > P1 = P3 e) P3 > P1 > P2
c)P1 > P2 = P3

9.  d) P2 > P3 > P1

10. Um mergulhador persegue um peixe a
5,0 m abaixo da superfície de um lago.
O peixe foge da posição A e se
esconde em uma gruta na posição B,
conforme mostra a figura. A pressão
atmosférica na superfície da água é
igual a pATM = 10 . 105 N/m2.
Adote g = 10 m/s2.

11. a) Qual a pressão sobre o mergulhador?
b) Qual a variação de pressão sobre o
peixe nas posições A e B?

12. a) De acordo com o teorema de Stevin:
pA = pATM + µ . g . h = 105 + 103 . 10 . 5
pA = 105 + 5 . 104 = 105 + 0,5 . 105
pA = 1,5 . 105
b) ∆pAB = µ . g . ∆hAB = 0
∆pAB = 0

13. Empuxo é igual ao peso do líquido deslocado
E = dL.g.VS

14. A figura mostra, em seqüências, um corpo
homogêneo: flutuando livremente num
líquido onde metade de seu volume fica
submerso; empurrado por uma força F1 que
o deixa parcialmente fora do líquido;
empurrado por uma força F2 que o deixa
com a parte superior encoberta por uma
finíssima camada de líquido; totalmente
mergulhado a profundidades diferentes por
ação das forças F3 e F4, respectivamente. Em
todos os casos o corpo está em equilíbrio
estático. O peso do corpo é P.

15. Observe que todas as forças estão identificadas
pelos seus módulos e assinale, abaixo, a
opção correta.
a) A força F1 é nula e a força F2 é igual a P.
b) As forças F2, F3 e F4 são iguais e maiores que P.
c) As forças F2, F3 e F4 são iguais e menores que F1.
d) As forças F3 e F4 são iguais e menores que F1 e F2.
e) A força F4 é igual a F3 e é maior que F1.

16. e) A força F4 é igual a F3 e é maior que F1.

17. Uma bóia de cortiça está totalmente submersa na água
de uma piscina, presa por um fio ideal, conforme
ilustra a figura:
Dados: Volume da bóia = 1,0 . 10–3 m3
µcortiça = 0,30 . 103 kg/m3
µágua = 1,0 . 103 kg/m3
g = 10 m/s2
Conclui–se que a força de tração no fio é:
a) 7,0 . 10o N
b) 7,0 . 10 N
c) 7,0 . 10–1 N
d) 7,0 . 10–2 N
e) 7,0 . 10–3 N

18. r
E
r r
T P

19. E=T+P
µL . Vim . g = T + mC . g
1 . 103 . 10–3 . 10 = T + µC . VC . g
10 = T + 0,3 . 103 . 10–3 . 10
10 – 3 = T ⇒ T = 7N
Gabarito: A

20. Um bloco com 140 kg de
massa e 0,02 m3 de volume,
está imerso em água e
suspenso por um conjunto
de cordas e polias, de
massa desprezível, como
indica a figura. Dados:
massa específica da água =
1000 kg/m3
g = 10 m/s2

21. A intensidade da força F que mantém o
sistema em equilíbrio é igual a:
a) 600 N d) 1200 N
b) 400 N e) 150 N
c) 300 N

22. T+E=P
T + d.g.VS = m . g
T + 1000.10.0,02=140.10
T + 200 = 1400
T = 1400 – 200
T = 1200 N
F = T/22
F = 1200/4
F = 300 N
Gabarito: C

23. O princípio de Pascal pode ser usado para
explicar como um sistema hidráulico
funciona.
Ex: Elevador hidráulico usado para
levantar um carro do solo para reparos
mecânicos.

24. A pressão aplicada a um fluido dentro de
um recipiente fechado é transmitida, sem
variação, a todas as partes do fluido, bem
como às paredes do recipiente.

25. Na prensa hidráulica na figura , os diâmetros
dos tubos 1 e 2 são , respectivamente, 4 cm e 20
cm. Sendo o peso do carro igual a 10000 N,
determine a força que deve ser aplicada no
tubo 1 para equlibrar o carro

26. A = π R2 R1= 2 cm R2= 10 cm
R2 = 5 R 1 A2 = 25A1
F1= 400 N

27. Uma garrafa é completamente preenchida com
água e fechada hermeticamente por meio de
uma rolha. Atravessa–se a rolha com um
estilete cilíndrico dotado de um suporte, como
mostra a figura. A área da seção transversal do
estilete é 1,0 . 10–5 m2 e a área do fundo da
garrafa é 1,0 . 10–2 m2. Aplica–se uma força
perpendicular ao suporte, de intensidade F =
1,0 N, de modo tal que a rolha permaneça
imóvel.
Em virtude da aplicação de , a intensidade da
força exercida no fundo da garrafa vale então:

28. a) 1,0 . 10–3 N F1 = F2
b) 1,0 . 103 N A1 A2
c)1,0 N 1 = F2 .
d) 1,0 . 105 N 10-5 10-2
F2 = 10 -2
10-5
F2 = 103 N
Gabarito: B

29. Numa preensa hidráulica, o êmbolo menor tem área de
10cm2 enquanto o êmbolo maior tem sua área de 100
cm2. Quando uma força de 5N é aplicada no êmbolo
menor , o êmbolo maior move-se. Pode-se concluir que
(A) a força exercida no êmbolo maior é de 500 N.
(B) o êmbolo maior desloca-se mais que o êmbolo
menor.
(C) os dois êmbolos realizam o mesmo trabalho.
(D) o êmbolo maior realiza um trabalho maior que o
êmbolo menor.
(E) O êmbolo menor realiza um trabalho maior que o
êmbolo maior

30. Gabarito: C