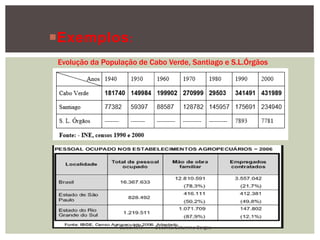
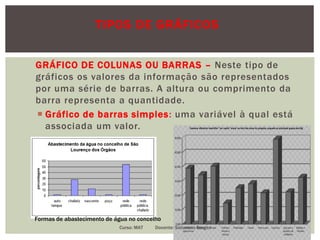
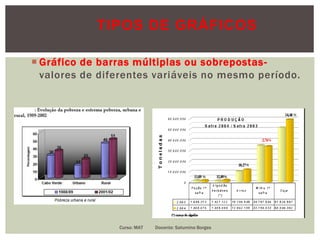
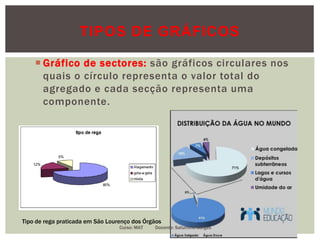
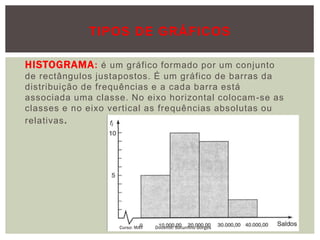
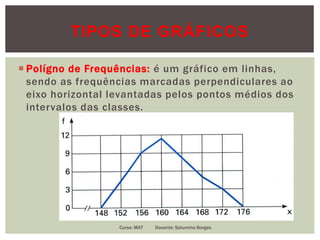
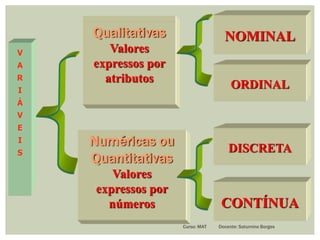
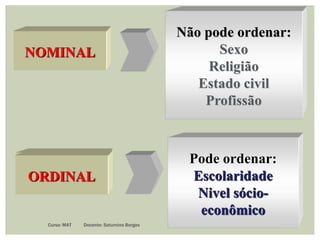
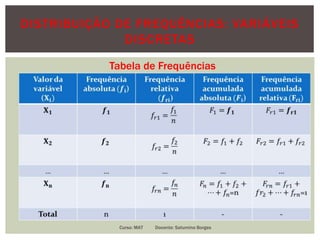
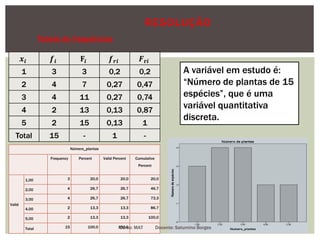
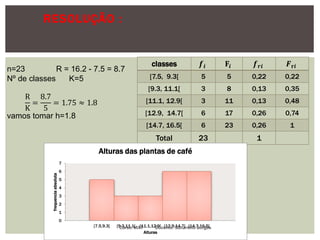
O documento apresenta conceitos fundamentais de estatística, incluindo estatística descritiva e inferência estatística, explicando a importância da coleta, organização e análise de dados. Ele aborda tópicos como variáveis, tipos de gráficos, tabelas de frequências, amostras e distribuição de dados, detalhando etapas e metodologias para representação de informações. Além disso, são discutidos aspectos de variáveis discretas e contínuas, e como representá-las graficamente.