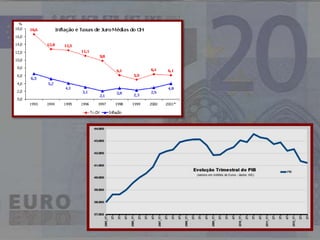
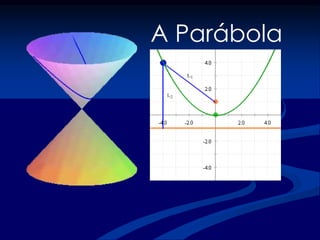
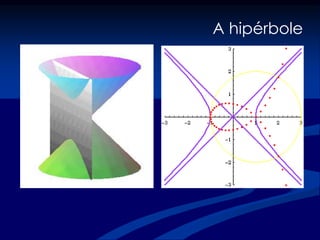
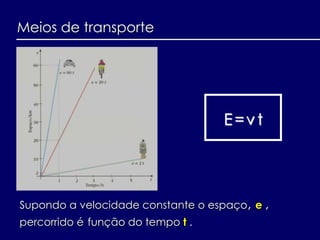
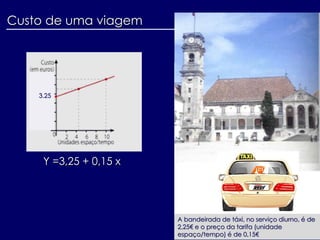
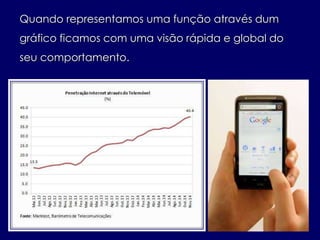
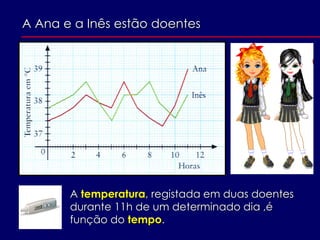
O documento discute a origem e aplicações de funções matemáticas. Descreve como funções são usadas para modelar fenômenos físicos e como evoluíram historicamente, desde os gregos até o desenvolvimento do cálculo no século XVII. Também fornece exemplos de como funções são usadas no dia a dia.

1. C531.A UTILIZAÇÃO DAS TIC NOS PROCESSOS DE ENSINO / APRENDIZAGEM 2014-2015
Formanda
Maria José Borges Dias da Silva
Formadores:
Elvira Rodrigues
Vítor Santos
As Funções
Origem, aplicações na Ciências e a ligação ao dia a dia

2. O Homem procura conhecer os fenómenos
naturais, sociais, económicos e culturais
que o rodeiam e interpretá-los, e
estabelecer leis que os regem.
Na generalidade das situações essas leis
são descritas pelas funções.
Introdução

3. Nas Ciências
A sua origem
No dia a dia
FUNÇÕES

5. Física

6. A altura, f(x), do projétil lançado
pelo canhão é função da distância
na horizontal, x, ao ponto de
lançamento.
Lançamento de um projétil

8. O alongamento da mola é função do peso suspenso.
Lei de Hooke

9. O volume ocupado pelo gás
é função da pressão.
(supondo a temperatura constante )
K
V =
P
Lei de Boyle-Mariotte

10. Arquimedes

11. A força exercida para levantar a pedra
é inversamente proporcional à distância
do ponto de apoio ao fulcro.Quanto
maior for a distância menor será a força
a exercer.

12. Lei de Ohm
A lei de Ohm estabelece uma relação de proporcionalidade
directa entre a diferença de potencial V, a intensidade de
corrente eléctrica I, e a resistência eléctrica R.
V = R I
V
I R

17. Arquitetura

18. Pelas suas propriedades
físicas , estéticas e
refletoras os arcos de
parábolas e hipérboles
surgem na Arquitetura em:
 Pontes
 Arcos
 Pórticos

19. A Parábola

20. Golden Gate Bridge
Arcos de água
Colégio Teresiano

21. Propriedade Refletora da Parábola
Farol de automóvel
Todo o raio luminoso que incide num espelho parabólico passando pelo
foco reflete-se paralelamente ao eixo.
Antena Parabólica

22. A hipérbole

24. As funções no dia a dia

25. Meios de transporte
Supondo a velocidade constante o espaço, e ,
percorrido é função do tempo t .
E=v t

26. Preços
O desconto ,y, obtido
pelos clientes é
diretamente
proporcional ao custo
inicial ,x, dos produtos.
y =0.4 x

27. Custo de uma viagem
Y =3,25 + 0,15 x
3.25
A bandeirada de táxi, no serviço diurno, é de
2,25€ e o preço da tarifa (unidade
espaço/tempo) é de 0,15€

28. Quando representamos uma função através dum
gráfico ficamos com uma visão rápida e global do
seu comportamento.

29. Custo de uma chamada telefónica

30. A Ana e a Inês estão doentes
A temperatura, registada em duas doentes
durante 11h de um determinado dia ,é
função do tempo.

32. Uma Introdução Histórica
O conceito de função é um dos mais
importantes da Matemática. Este conceito
sofreu uma grande evolução ao longo dos
séculos, sendo que a introdução do método
analítico na definição de função (sec., XVI,
sec.XVII ) veio revolucionar a Matemática.
Desde o tempo dos Gregos até à
Idade Moderna a teoria dominante
era a Geometria Euclidiana que tinha
como elementos base o ponto, a
recta e o plano.

33. Em fins do século XVI, princípios do século XVII, com os
trabalhos de Kepler sobre os movimentos dos planetas
e os de Galileu relativos à queda dos graves, a
Matemática começa a ser aplicada com êxito ao estudo
dos movimentos ( Cinemática e Dinâmica ).
A análise matemática surge
agora, baseada no conceito de
de função. Os seres matemáticos
dão-se-nos a conhecer pelas
suas variações impressionando
os nossos sentidos ;
mas também não seria possível
conhecê-los, se nessas variações
não houvesse uma lei, isto é,
uma propriedade ou uma relação
sensivelmente constante.

34. René Descartes ( França 1596-
1650 ), revolucionou a
Matemática e a Ciência ao
associar um sistema de eixos,
um ponto (P) e um par de
números (x,y) que chamou
abcissa (x) e ordenada (y) o
que permitiu a representação
das funções num gráfico.
Ora, as leis dos fenómenos são expressas por
funções. São pois os conceitos matemáticos de
variável e de função que permitem à razão humana
interpretar o movimento e, de um modo geral os
fenómenos naturais.
René Descartes

35. Foi Leibniz (1646-1716) ao
analisar uma curva à procura de
extremos que introduziu o termo
função na Matemática.
No entanto foi o matemático suiço
Euler (17o7-1783) quem utilizou
pela primeira vez y = f(x) .
Leibniz
Assim o conceito de função
que hoje nos aparece simples
é resultado de uma evolução
histórica conduzindo sempre
cada vez mais abstração, e
que só no século XIX teve o
seu final.
Euler

36. C531.A UTILIZAÇÃO DAS TIC NOS PROCESSOS DE ENSINO / APRENDIZAGEM 2014-2015
Formanda
Maria José Borges Dias da Silva
Formadores:
Elvira Rodrigues
Vítor Santos
As Funções
Origem, aplicações na ciências e a ligação ao dia a dia
Obrigada pela atenção!