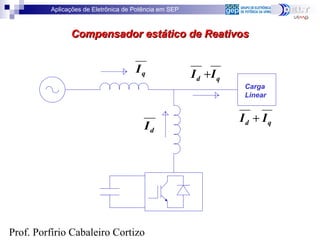
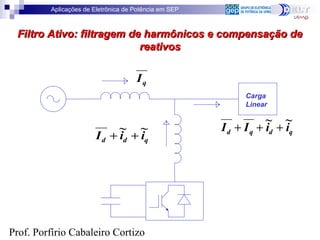
O documento aborda aplicações de eletrônica de potência em sistemas elétricos, incluindo regulação de tensão, correção de fator de potência e filtragem de harmônicos. Descreve conceitos de potência ativa e reativa, transformações de Clarke e Park, e suas implicações em sistemas trifásicos. A análise inclui a influência de harmônicos e as definições de potência em diferentes contextos.



![Aplicações de Eletrônica de Potência em SEP
Prof. Porfírio Cabaleiro Cortizo
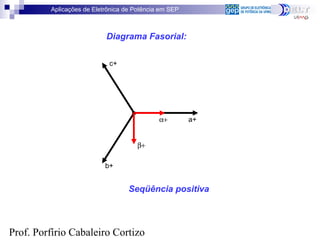
Definições de Potência Ativa e Potência Reativa
:seráainstantânePotênciaA
:quedoConsideran
)tsin(.I.2)t(i
)tsin(.V.2)t(v
a
a
ϕω
ω
−=
=
[ ]
[ ] )t2sin(.Q)t2cos(1.P)t(p
)V.I.sin(ReativaPotência
)V.I.cos(AtivaPotência
:definindoe
)t2sin().sin(.I.V)t2cos(1).cos(.I.V)t(p
)tsin().tsin(.I.V2)t(i).t(v)t(p aa
ωω
ϕ
ϕ
ωϕωϕ
ϕωω
−−=
=
=
−−=
−==](https://image.slidesharecdn.com/45079-150108164326-conversion-gate02/85/Conversao-Referenciais-Motor-CA-3F-4-320.jpg)

![Aplicações de Eletrônica de Potência em SEP
Prof. Porfírio Cabaleiro Cortizo
Considerando a presença de harmônicos tanto na
tensão quanto na corrente de carga, temos:
:a seráinstantânePotênciaA
)tnsin(.I.2)tsin(.I.2)t(i
)tmsin(.V.2)tsin(.V.2)t(v
:quedoConsideran
2n
nn11a
2m
m1a
∑
∑
∞
=
∞
=
−+−=
+=
ϕωϕω
ωω
[ ]
[ ] [ ]{ }
[ ] [ ]{ }
[ ] [ ]{ }∑∑
∑
∑
∞
=
∞
=
∞
=
∞
=
−+−+−+
+−+−+−+
+−+−−−+
+−−=
2n 2m
nnnm
2m
111m
2n
nnn1
111111
t)nm(cost)nm(cosIV
t)1m(cost)1m(cosIV
t)1n(cost)1n(cosIV
)t2sin().sin(.I.V)t2cos(1).cos(.I.V)t(p
ϕωϕω
ϕωϕω
ϕωϕω
ωϕωϕ](https://image.slidesharecdn.com/45079-150108164326-conversion-gate02/85/Conversao-Referenciais-Motor-CA-3F-6-320.jpg)


























![Aplicações de Eletrônica de Potência em SEP
Prof. Porfírio Cabaleiro Cortizo
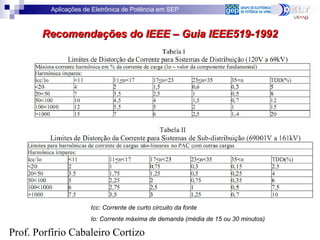
Norma IEC 6100Norma IEC 6100
Ordem da Harmônica (n) Classe A Classe B Classe C (>25W) Classe D Classe D
Máx. Corrente Máx. Corrente % da Fundamental ((>10W, <300W) (A)
(A) (A) [ma/W]
Harmônicas Ímpares
3 2,3 3,45 30*FP 3,4 2,3
5 1,14 1,71 10 1,9 1,14
7 0,77 1,155 7 1 0,77
9 0,4 0,6 5 0,5 0,4
11 0,33 0,495 3 0,35 0,33
13 0,21 0,315 3 0,296 0,21
15≤n≤39 3 3,85/n 2,25/n
Harmônicas Pares
2 1,08 1,62 2
4 0,43 0,645
6 0,3 0,45
8≤n≤40
FP = Fator de Potência
Tabela V – Limite das componentes harmônicas da corrente em 230V](https://image.slidesharecdn.com/45079-150108164326-conversion-gate02/85/Conversao-Referenciais-Motor-CA-3F-37-320.jpg)