Este documento apresenta a resolução de 37 problemas de física relacionados a circuitos elétricos. As soluções envolvem a aplicação das leis de Kirchhoff para análise de circuitos, cálculo de correntes e tensões. Os problemas abordam tópicos como cálculo de potência máxima dissipada, determinação de correntes em circuitos complexos e análise de circuitos com múltiplas fontes.

1. PROBLEMAS RESOLVIDOS DE FÍSICA
Prof. Anderson Coser Gaudio
Departamento de Física – Centro de Ciências Exatas – Universidade Federal do Espírito Santo
http://www.cce.ufes.br/anderson
anderson@npd.ufes.br Última atualização: 30/08/2005 13:07 H
RESNICK, HALLIDAY, KRANE, FÍSICA, 4.ED.,
LTC, RIO DE JANEIRO, 1996.
FÍSICA 3
Capítulo 33 - Circuitos de
Corrente Contínua
Problemas
01 02 03 04 05 06 07 08 09 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58

2. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
Problemas Resolvidos
20. Uma fonte de potência de 120 V é protegida por um fusível de 15 A. Qual o número máximo de
lâmpadas de 500 W que podem ser simultaneamente alimentadas, em paralelo, por esta fonte?
(Pág. 127)
Solução.
Considere o esquema abaixo, onde F é um fusível e L é lâmpada:
V
Fi0
P P P
LNL2L1
i i i
Como as lâmpadas L1, L2, ... , LN estão associadas em paralelo, todas estão sujeitas à mesma
diferença de potencial V. Logo, a corrente elétrica em cada uma delas vale:
P
i
V
= (1)
A soma das correntes que abastecem as lâmpadas deve ser, no máximo, igual a i0:
(2)0 1 2 Ni i i i N= + + + = i
Substituindo-se (1) em (2):
0
P
i N
V
=
0i V
N
P
= lâmpadas
(15 A)(120 V)
3,6
(500 W)
N = = lâmpadas
Como não pode haver número fracionário de lâmpadas:
N = 3 lâmpadas
[Início]
26. No circuito da Fig. 23, ε, R1 e R2 têm valores constantes, mas R pode variar. Ache uma
expressão para R que torne máximo o aquecimento deste resistor.
(Pág. 128)
Solução.
Considere o esquema abaixo, que representa a parte superior central do circuito, onde 1 e 2
representam as malhas da esquerda e da direita, respectivamente, e in representam as correntes
elétricas:
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4
a
Ed. - LTC - 1996. Cap. 33 - Circuitos de Corrente Contínua
2

3. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
i0 i2
i1
1 2
Potência dissipada por R:
(1)2
( ) 2RP i= R
Cálculo de i2 (leis de Kirchhoff):
(2)0 1 2i i i= +
1 0 2 1 0R i R iε − − = (3)
(4)2 2 1 0Ri R i− + =
Resolvendo-se o sistema (2), (3) e (4):
( )
2
2
1 2 1 2
R
i
R R R R R
ε
=
+ +
(5)
Substituindo-se (5) em (1):
( )
2 2
2
( ) 2
1 2 1 2
R
R R
P
R R R R R
ε
=
+ +⎡ ⎤⎣ ⎦
Valor de R que maximiza a dissipação de calor em R:
( )
0RdP
dR
=
( )
( )
2 2
2 1 2 1 2
3
1 2 1 2
0
R R R R R R
R R R R R
ε − +⎡ ⎤⎣ ⎦ =
+ +⎡ ⎤⎣ ⎦
Como todas as grandezas que aparecem no primeiro membro desta equação são positivas, ela só
será verdadeira se:
( )1 2 1 2 0R R R R R− + =
Logo:
1 2
1 2
R R
R
R R
=
+
[Início]
33. Qual a leitura no amperímetro A, Fig. 27,ε e R? Suponha que A tenha resistência interna nula.
(Pág. 128)
Solução.
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4
a
Ed. - LTC - 1996. Cap. 33 - Circuitos de Corrente Contínua
3
Considere o esquema simplificado da Fig. 27 abaixo:

4. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
i1 i2
i3
i6
i4
i5
A
B
C
a
b c
d
Equações de Kirchhoff para o circuito.
Nó a:
1 2i i i= + 3
4
5
Nó b:
6 3i i i= +
Nó c:
2 4i i i= +
Malha A:
3 62 0Ri Riε − − =
Malha B:
3 22 0Ri Ri− =
Malha C:
6 5 0Ri Ri− =
As equações acima formam um sistema com seis incógnitas. A solução é laboriosa e tem o seguinte
resultado:
1
6
7
i
R
ε
=
,
2
4
7
i
R
ε
=
,
3
2
7
i
R
ε
=
,
4
7
i
R
ε
=
,
5
3
7
i
R
ε
=
,
6
3
7
i
R
ε
=
A corrente que passa pelo amperímetro é i4. Logo, a resposta do problema é:
4
7
i
R
ε
=
[Início]
34. Quando as luzes de um carro são ligadas, um amperímetro em série com elas marca 10,0 A e um
voltímetro em paralelo marca 12,0 V. Veja a Fig. 28. Quando o motor de arranque elétrico é
ligado, a leitura no amperímetro baixa para 8,00 V e as luzes diminuem um pouco seu brilho. Se
a resistência interna da bateria for 50 mΩ e a do amperímetro for desprezível, quais são (a) a
fem da bateria e (b) a corrente que atravessa o motor de arranque quando as luzes estão acesas?
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4
a
Ed. - LTC - 1996. Cap. 33 - Circuitos de Corrente Contínua
4

5. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
(Pág. 128)
Solução.
(a) Quando as luzes são ligadas, mas o motor de arranque ainda está desligado, o circuito pode ser
representado pela figura abaixo, onde ε é a fem da bateria, R é a resistência interna da bateria, i0 é a
corrente elétrica e L representa as luzes do carro:
L
R
ε
i0
Aplicação da regra das malhas de Kirchhoff a este circuito, onde V é a diferença de potencial nos
terminais das luzes:
0 0V Riε − − =
0V Riε = +
3
(12,0 V) (50 10 )(10,0 A)ε −
= + × Ω
12,5 Vε =
(b) Quando o motor de arranque é ligado, o circuito passa a ser representado pela figura abaixo,
onde M representa o motor de arranque:
L
R
ε
i1
M
i2 i3
Aplicação das regras de Kirchhoff a este circuito, onde RM é a resistência elétrica do motor e RL é a
resistência das luzes:
2 1 0MR i Riε − − = (1)
(2)3 2 0L MR i R i− + =
(3)1 2i i i= + 3
(1) + (2):
1 3 0LRi R iε − − = (4)
Resistência das luzes, obtida do circuito analisado no item (a):
0
L
V
R
i
= (5)
Resolvendo-se (4) para i1 e substituindo-se (5):
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4
a
Ed. - LTC - 1996. Cap. 33 - Circuitos de Corrente Contínua
5

6. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
1 3
0
1V
i i
i R
ε
⎛ ⎞
= −⎜ ⎟
⎝ ⎠
1 3
(12,0 V) 1
(12,5 V) (8,00 A) 58,0
(10,0 A) (50 10 )
i −
⎡ ⎤
= − =⎢ ⎥ × Ω⎣ ⎦
Ω
3
Resolução de (3):
2 1i i i= −
2 (58,0 A) (8,00 A)i = −
2 50,0 Ai =
[Início]
35. A Fig. 29 mostra uma bateria ligada a um resistor uniforme R0. Um contato deslizante pode
mover-se sobre o resistor de x = 0 à esquerda, até x = 10 cm à direita. Ache uma expressão para
a potência dissipada no resistor R como uma função de x. Trace o gráfico desta função para ε =
50 V, R = 2.000 Ω e R0 = 100 Ω.
(Pág. 128)
Solução.
Considere o esquema simplificado da Fig. 29 abaixo:
i1
i2
i3
A
B
a
L
x
Potência dissipada no resistor R:
(1)2
3P Ri=
O cálculo da potência está na dependência de i3, que será calculado por meio da aplicação equações
de Kirchhoff ao circuito.
Nó a:
(2)1 2 3i i i− =
Malha A:
2 0 1 0 0
x L x
i R i R
L L
ε
−⎛ ⎞ ⎛ ⎞
− −⎜ ⎟ ⎜ ⎟
⎝ ⎠ ⎝ ⎠
=
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4
a
Ed. - LTC - 1996. Cap. 33 - Circuitos de Corrente Contínua
6

7. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
( )1 2 0 1 0 0
x
i i R i R
L
ε + − − = (3)
Substituindo-se (2) em (3):
3
0 1 0 0
i x
R i R
L
ε + − = (4)
Malha B:
3 1 0 0
L x
i R i R
L
ε
−⎛ ⎞
− − =⎜ ⎟
⎝ ⎠
(5)
Multiplicando-se ambos os membros de (5) por L
L x
⎛ ⎞
−⎜ ⎟
−⎝ ⎠
3 1 0
L L
i R i R
L x L x
ε
⎛ ⎞ ⎛ ⎞
− + +⎜ ⎟ ⎜ ⎟
− −⎝ ⎠ ⎝ ⎠
0 = (6)
(4) + (6):
3
0 3 1 0 1 0 0
i xL L
R i R i R i R
L x L L x
ε ε
⎛ ⎞ ⎛ ⎞
− + + − +⎜ ⎟ ⎜ ⎟
− −⎝ ⎠ ⎝ ⎠
=
3 01 0
L x L
i R R
L x L L x
ε
⎛ ⎞ ⎛ ⎞
− + +⎜ ⎟ ⎜ ⎟
− −⎝ ⎠ ⎝ ⎠
=
2
0
3
( ) ( )
( )
L x xR L R L L x
i
L L x L x
ε
⎡ ⎤− + − −⎡ ⎤
=⎢ ⎥ ⎢ ⎥− −⎣ ⎦⎣ ⎦
3 2
0 ( )
Lx
i
L R R L x x
ε
=
+ −
(7)
Substituindo-se (7) em (1):
2 2 2
22
0 ( )
L Rx
P
L R R L x x
ε
=
⎡ ⎤+ −⎣ ⎦
(b)
x
P(x)
[Início]
37. (a) Calcule a intensidade das três correntes que aparecem no circuito da Fig. 31. (b) Calcule o
valor de Vb − Va. Suponha que R1 = 1,20 Ω, R1 = 2,30 Ω, ε1 = 2,00 V, ε2 = 23,80 V e ε3 = 5,00
V.
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4
a
Ed. - LTC - 1996. Cap. 33 - Circuitos de Corrente Contínua
7

8. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
(Pág. 129)
Solução.
(a) Considere o esquema simplificado da Fig. 31 abaixo:
i1
i2
i3
A B
a
b
c
Equações de Kirchhoff.
Malha A:
1 1 1 2 2 2 1 1 0R i R i R iε ε− − − − =
1 2 1 1 2 22R i R i 0ε ε− − − = (1)
Malha B:
3 1 3 2 2 2 1 3 0R i R i R iε ε− − − − =
3 2 1 3 2 22R i R i 0ε ε− − − = (2)
Nó a:
(3)1 2i i i= − 3
0
Substituindo-se (3) em (1):
1 2 1 2 1 3 2 22 2R i R i R iε ε− − + − = (4)
(2) + (4):
( )1 2 3 1 2 22 2 R R iε ε ε− + − + = 0
( )
1 2
2
1 2
2
2
i 3
R R
ε ε ε− +
=
+
(5)
[ ]2
(2,00 V) 2(3,80 V) (5,00 V)
0,085714 A
2 (1,20 ) (2,30 )
i
− +
= =
Ω + Ω
−
2 85,7 mAi ≈ −
Logo, a corrente i2 tem o sentido para cima.
Substituindo-se (5) em (2):
( )
2 1 3 1 1 2 3 2
3
1 1 2
2 2
4
R R R R
i
R R R
ε ε ε ε− − − +
=
+
(6)
3 0,582 Ai ≈
Logo, a corrente i3 tem o sentido para cima.
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4
a
Ed. - LTC - 1996. Cap. 33 - Circuitos de Corrente Contínua
8

9. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
Substituindo-se (6) em (5):
( )
1 1 2 1 1 2 3 2
1
1 1 2
2 2
4
R R R R
i
R R R
ε ε ε ε− + −
=
+
1 0,668 Ai ≈ −
Logo, a corrente i1 tem o sentido para baixo.
(b) Contabilidade de ganhos e perdas de potencial elétrico no caminho ab, considerando-se o
sentido correto da corrente i2 (para cima):
2 2 2b aV R i Vε+ − =
2 2 2b aV V R i ε− = −
(2,30 )(0,668 A) (3,80 V) 3,60285 Vb aV V− = Ω − = −
3,60 Vb aV V− ≈ −
[Início]
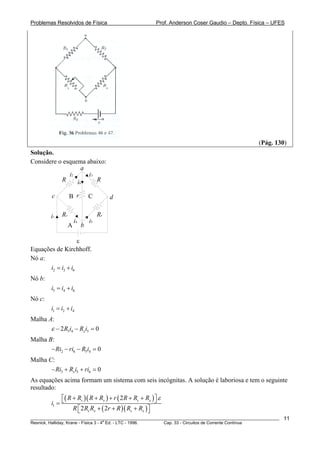
46. A resistência variável da Fig. 36 pode ser ajustada de modo que os pontos a e b tenham
exatamente o mesmo potencial. (Verificaremos essa situação ligando momentaneamente um
medidor sensível entre os pontos a e b. Não havendo diferença de potencial, não haverá
deslocamento no ponteiro do medidor.) Mostre que, após essa ajustagem, a seguinte relação
torna-se verdadeira:
2
1
X S
R
R R
R
= ,
A resistência (Rx) de um resistor pode ser medida por este processo (chamado de Ponte de
Wheatstone), em função das resistências (R1, R2 e R3) de outros resistores calibrados
anteriormente.
(Pág. 130)
Solução.
Considere o esquema abaixo:
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4
a
Ed. - LTC - 1996. Cap. 33 - Circuitos de Corrente Contínua
9

10. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
i1
i0
i2
a
c d
b
R R
RxRs
ε
Contabilidade de ganhos e perdas de potencial elétrico no caminho adb:
1 1 2a S bV R i R i V V+ − = = a
1 1 2SR i R i= (1)
Contabilidade de ganhos e perdas de potencial elétrico no caminho acb:
2 1 2a X bV R i R i V V− + = = a
2 1 2XR i R i= (2)
Dividindo-se (1) por (2):
1
2
S
X
RR
R R
=
2
1
X S
R
R R
R
=
[Início]
47. Mostre que se os pontos a e b da Fig. 36 forem ligados por um fio de resistência r este será
percorrido por uma corrente igual a
( )
( )( )2 2
s x
s x s
R R
i
R r R R R R
ε −
=
+ + + x
,
onde fizemos R1 = R2 = R,R0 = 0, e ε é o valor da fem da bateria. Esta fórmula é consistente com
o resultado do problema 46?
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4
a
Ed. - LTC - 1996. Cap. 33 - Circuitos de Corrente Contínua
10

11. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
(Pág. 130)
Solução.
Considere o esquema abaixo:
i2
i1
i3
i5i4
i6
B C
A
a
c d
b
R R
RxRs
r
ε
Equações de Kirchhoff.
Nó a:
2 3i i i= + 6
6
4
Nó b:
5 4i i i= +
Nó c:
1 2i i i= +
Malha A:
5 4 52 0xR i R iε − − =
Malha B:
2 6 5 4 0Ri ri R i− − − =
Malha C:
3 5 6 0xRi R i ri− + + =
As equações acima formam um sistema com seis incógnitas. A solução é laboriosa e tem o seguinte
resultado:
( )( ) ( )
( )( )1
2
2 2
s x s x
s x s x
R R R R r R R R
i
R R R r R R R
ε+ + + + +⎡ ⎤⎣ ⎦=
+ + +⎡ ⎤⎣ ⎦
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4
a
Ed. - LTC - 1996. Cap. 33 - Circuitos de Corrente Contínua
11

12. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
( ) ( )
( )( )2
2 2
s x s x
s x s x
R R R r R R
i
R R R r R R R
ε+ + +⎡ ⎤⎣ ⎦=
+ + +⎡ ⎤⎣ ⎦
( )
( )( )3
2 2
s s x
s x s x
rR r R R R
i
R R R r R R R
ε+ + +⎡ ⎤⎣ ⎦=
+ + +⎡ ⎤⎣ ⎦
( )
( )( )4
2
2 2
x
s x s
r R R
i
R R r R R R
ε+ +
=
+ + + x
( )
( )( )5
2
2 2
s
s x s
r R R
i
R R r R R R
ε+ +
=
+ + + x
( )
( )( )6
2 2
s x
s x s
R R
i
R R r R R R
ε−
=
+ + + x
A corrente que passa por r é i6. Logo, a demonstração está completa.
[Início]
51. Um capacitor é descarregado, através de um circuito RC, fechando-se a chave no instante t = 0.
A diferença de potencial inicial através do capacitor é igual a 100 V. Se a diferença de potencial
baixou para 1,06 V após 10,0 s, (a) qual é a constante de tempo do circuito? (b) Qual será a
diferença de potencial no instante t = 17 s?
(Pág. 130)
Solução.
Considere o esquema abaixo:
C R
(a) Equação de descarga do circuito RC, onde q(t) é a carga elétrica nas placas do capacitor em
função do tempo e q0 é a carga inicial nas placas:
(1)/
( ) 0
t RC
tq q e−
=
Diferença de potencial nas placas do capacitor em função do tempo:
( )
( )
t
t
q
V
C
= (2)
Substituindo-se (2) em (1):
/0
( )
t RC
t
q
V e
C
−
=
(3)/
( ) 0
t RC
tV V e−
=
( ) /
0
t t RC
V
e
V
−
=
( )
0
ln tV t
V R
⎛ ⎞
= −⎜ ⎟
⎝ ⎠ C
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4
a
Ed. - LTC - 1996. Cap. 33 - Circuitos de Corrente Contínua
12

13. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
( )
0
ln t
t
RC
V
V
= −
⎛ ⎞
⎜ ⎟
⎝ ⎠
(10,0 s)
2,1993 s
1,06 V
ln
100 V
RC = − =
⎛ ⎞
⎜ ⎟
⎝ ⎠
2,20RC s≈
(b) Partindo-se de (3):
/
( ) 0
t RC
tV V e−
=
(17 s)/(2,1993 s)
(17 s) 0(100 V) 0,043956 VV e−
= =
(17 s) 0,0440 VV ≈
[Início]
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4
a
Ed. - LTC - 1996. Cap. 33 - Circuitos de Corrente Contínua
13