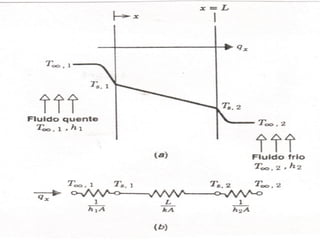
O documento discute a equação da difusão do calor, que é crucial para entender a distribuição de temperatura e seu impacto na integridade estrutural de sólidos. Ele aborda conceitos como geração de calor, fluxo de calor e condições de contorno, usando exemplos práticos e simplificações para fluxos unidimensionais. Além disso, o texto relaciona a condução de calor à resistência térmica, utilizando analogias com circuitos elétricos.

1. Capítulo 2
Equação da Difusão do Calor
( Equação da distribuição de temperatura )

2. • O conhecimento da distribuição de
temperatura pode ser usado para o
julgamento da integridade estrutural num
sólido, através da determinação de
tensões, expansões e deflexões térmicas.
Também pode ser usada para se otimizar
a espessura de um material isolante ou
para determinar a compatibilidade entre
um revestimento e o material. Através da
distribuição de temperatura num meio é
possível determinarmos o fluxo de calor.

3. T (x, y, z)

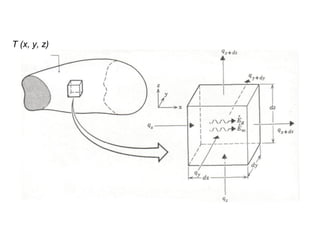
4. Equação de balanço
( Conservação de energia )
[ Fluxo de calor + Fluxo de calor - Fluxo de calor = Fluxo de calor]
entra gerado sai armazenado
Fluxo de calor que entra → qx + qy + qz
y
T
kdxdz
qy


−
=
x
T
kdydz
qx


−
=
z
T
kdxdy
qz


−
=

5. Fluxo de calor que sai → qx+dx + qy+dy + qz+dz
Pela série de Taylor, temos:
z
z
z
z
z
y
y
y
y
y
x
x
x
x
x
d
z
q
q
d
q
d
y
q
q
d
q
d
x
q
q
d
q






+
=
+
+
=
+
=
+ +
;
;

6. Sendo:
dxdydz
z
z
T
k
dz
q
q
dxdydz
y
y
T
k
dy
q
q
dxdydz
x
x
T
k
dx
q
q
z
z
y
y
x
x












)
(
)
(
)
(
=
+
−
=
+
−
=
+
− Eq. 2.2
Eq. 2.3
Eq. 2.4

7. Fluxo de calor gerado ( Eg ) → qger = q dxdydz Eq. 2.5
Dentro de um meio pode haver uma fonte de
energia que proporciona um termo associado à
taxa de geração de energia térmica. Esta
geração é a manifestação de um processo de
conversão de energia elétrica, química ou
nuclear em energia térmica. O termo é positivo
se há uma fonte e negativo de consome
energia ( sorvedouro). Exemplos: bobinas
elétricas, combustão, reatores, etc.

8. qº - representa a taxa de geração de energia por
unidade de volume ( W/m3 )
Fluxo de calor armazenado (Eac) →
Eq. 2.6
O fluxo acumulado está associado a variação de
energia interna, ou seja a mudança do estado térmico.
Caso este termo exista, o corpo estará se resifriando ou
se aquecendo.
Substituindo as equações 2.2 a 2.6 em 2.1 e dividindo
pelo volume dxdydz, temos:
dxdydz
t
T
C
q p
arm



=

9. t
T
C
q
z
T
k
z
y
T
k
y
x
T
k
x
p















=
+
+
+ )
(
)
(
)
( Eq. 2.7
Equação da difusão do calor
Eq. 2.7
Os três primeiros termos da equação referem-se a um
fluxo ser unidimensional (T varia somente com x),
bidimensional (a T varia com x e com y) ou
tridimendional ( a T varia nas três dimensões x, y e z).

10. O termo q é o termo de calor gerado;
e a ser o tipo de regime (permanente ou transiente).
Considerando k como sendo constante com a
temperatura, temos:
Eq.2.8
onde α = coeficiente de difusividade térmica (m²/s),
mede a relação entre a capacidade do material em
conduzir energia e sua capacidade em acumular
energia
t
T
Cp



t
T
k
q
z
T
y
T
x
T








alfa
1
²
²
²
²
²
²
)
(
)
(
)
( =
+
+
+
p
C
k
alfa

=

11. Estudaremos casos simplificados da equação da
distribuição de temperatura:
a) Fluxo de calor unidimensional, sem
geração de calor e regime permanente:
b) Fluxo de calor unidimensional, com geração de
calor e regime permanente:
0
)
( =
+ q
x
T
k
x 



0
)
( =
x
T
k
x 




12. c) Fluxo de calor unidimensional, sem
geração de calor e regime transiente:
d) Fluxo de calor bidimensional, sem
geração de calor e regime permanente:
0
)
(
)
( =
+
y
T
k
y
x
T
k
x 







t
T
C
x
T
k
x
p







=
)
(

13. Também podemos usar a equação da difusão de
calor em coordenadas cilíndricas ou esféricas.
- Coordenadas cilíndricas
- Coordenadas esféricas
t
T
C
q
z
T
k
z
T
k
r
r
T
kr
r
r
p















=
+
+
+ )
(
)
(
)
( /
0
/
0
²
1
1
t
T
C
q
T
ksen
sen
r
T
k
sen
r
r
T
kr
r
r
p















=
+
+
+ )
(
)
(
)
( 0
0
0
0
²
²
1
/
0
/
0
0
²
²
1
²
²
1

14. 2.2 Equacionamento Diferencial (Condições
de Contorno e Condições iniciais )
Condição de contorno é uma afirmação
matemática relativa ao comportamento da
variável dependente.
As condições de contorno ( c.c. ) especificam a
condição térmica na superfície das fronteiras da
região.
• Condições utilizadas:
• temperatura
• fluxo de calor especificado
• condições de contorno convectivas ( balanço)

16. -A condição de temperatura constante é
chamada de condição de Dirichlet ou condição
de contorno de 1° espécie. Exemplo sólido em
fusão ou líquido em ebulição.
-A condição de fluxo de calor constante é
chamada de condição de Neumann ou
condição de contorno de 2° espécie. Exemplo
Justapor um calefator elétrico.
-A condição convectiva corresponde ao
aquecimento ou resfriamento na superfície
(Balanço).

17. • Ver o Exemplo 2-3 Incropera 8ed.

18. Capítulo 3
Condução Unidimensional
em Regime Permanente

19. • Num sistema unidimensional os
gradientes de temperatura existem
somente ao longo de uma única
coordenada, e a transferência de calor
ocorre exclusivamente nesta direção.
• Em regime permanente a temperatura
é independente do tempo.
•  Objetivo: Expressar a distribuição de
temperatura e a taxa de calor.

20. Parede Plana
• A temperatura é função exclusivamente
da coordenada x e o calor se transfere
somente nesta direção.
• Considere a figura abaixo - Uma
parede que separa dois fluidos de
temperaturas diferentes.

22. • Considerando regime permanente, fluxo
unidimensional e sem geração de calor, a
equação da difusão de calor se resume a:
; Considerando K constante
com temperatura e integrando temos,
integrando novamente temos:
d
dx
k
dT
dx





 = 0
k
dT
dx
C
= 1

23. T = C1 .x + C2 Eq. 3.1
As condições de contorno são:
p/ x= 0  T= Ts1
p/ x= L  T= Ts2

24. Substituindo as c.c. cc1 
cc2 
Temos:
Observamos que a distribuição de
temperatura é linear.
C Ts
2 1
=
( )
C
T T
L
s s
1
2 1
=
−
( )
T T T
x
L
T
s s s
= − +
2 1 1

25. O fluxo de calor 
ou
( )
q kA
dT
dx
KA
T T
L
x
s s
= − = −
−
2 1
)
( 2
1
"
s
s
x T
T
L
k
q −
=

26. Resistência Térmica
• Lei de Ohm
• U = R.i - A diferença de potencial
(medida) é proporcional a intensidade de
corrente pela resistência.
• Podemos resolver problemas de
transferência de calor por analogia com a
Lei de Ohm.

27. U1 U2 T1 T2
i Equivalente q 
R Rt
Resistência térmica
É a oposição que o material oferece a
passagem do calor.
Parede Plana

q KA
T
x
x =

q
T
x kA
x =

/

28. Logo a resistência térmica será Rt= x/kA
T1 T2
Circuito q 
x/kA
Este conceito é muito utilizado para paredes
compostas, ou seja uma associação de
materiais diferentes.

29. Resistência térmica de contato
( Rt” - K/Wm2 )
A resistência térmica de contato pode ser atribuída
a rugosidade da superfície. Quando fazemos a
junção de materiais diferentes ocorre a
formação de “ buracos” que contém ar, portanto
ocorrerá uma resistência a passagem do calor.
Essa troca será por condução e radiação. Essa
resistência pode ser minimizada através do uso
de graxas, metais moles, ceras etc, que
possuem um alto coeficiente de condutividade
térmica.

30. Exemplos
3-1 – Observar o arranjo em paralelo entre a
convecção e a radiação
Para isso linearizamos o hrad
É obtido por qconv = qrad
hradA(Tsup-Tviz )= ƐσA(T4
sup-T4
viz )
hrad= Ɛσ(T2
sup+T2
viz ) (Tsup+Tviz )
Exemplo 3-2 (Fluxo Unidimensional )