Este documento apresenta 64 problemas resolvidos de física sobre o capítulo 34 - O Campo Magnético do livro Física 3 de Resnick, Halliday e Krane. Os problemas abordam conceitos como campo magnético criado por correntes elétricas, força sobre cargas em movimento em campo magnético, momento magnético e torque. As soluções fornecem detalhes dos cálculos e raciocínios físicos envolvidos em cada problema.

1. PROBLEMAS RESOLVIDOS DE FÍSICA
Prof. Anderson Coser Gaudio
Departamento de Física – Centro de Ciências Exatas – Universidade Federal do Espírito Santo
http://www.cce.ufes.br/anderson
anderson@npd.ufes.br Última atualização: 30/08/2005 12:02 H
RESNICK, HALLIDAY, KRANE, FÍSICA, 4.ED.,
LTC, RIO DE JANEIRO, 1996.
FÍSICA 3
Capítulo 34 - O Campo
Magnético
Problemas
01 02 03 04 05 06 07 08 09 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64

2. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
Problemas Resolvidos
16. Um feixe de elétrons, cuja energia cinética é K, emerge de uma lâmina fina na “janela” da
extremidade do tubo de um acelerador. Existe uma placa de metal, perpendicular à direção do
feixe emergente, a uma distância d desta janela. Veja Fig. 30. (a) Mostre que podemos evitar
que o feixe colida com a placa aplicando um campo magnético B, tal que
2mK
B≥ ,
e2 d 2
onde m e e são a massa e a carga do elétron. (b) Qual deve ser o sentido de B?
y
z x
(Pág. 150)
Solução.
(a) Para seguir a trajetória descrita no esquema acima, o feixe de elétrons deve interagir com um
campo magnético que tenha a direção +z. A trajetória será circular com raio d e força centrípeta
igual à força magnética sobre os elétrons.
Fc = Fm
mv 2
= evB
d
mv
B=
ed
m2v 2
B2 = (1)
e2 d 2
Velocidade dos elétrons:
1
K = mv 2
2
2K
v2 = (2)
m
Substituindo-se (2) em (1):
⎛ 2K ⎞
m2 ⎜ ⎟
B2 = ⎝ m ⎠ = 2mK
e2 d 2 e2 d 2
2mK
B= (3)
ed
________________________________________________________________________________________________________ 2
a
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996. Cap. 34 - O Campo Magnético

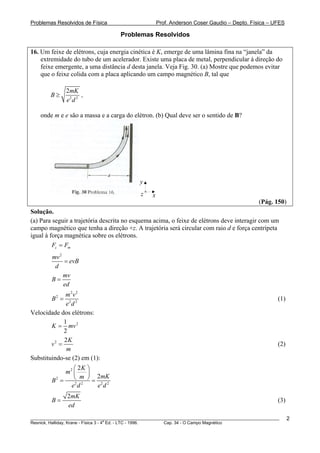
3. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
Para este valor de campo magnético o feixe de elétrons irá tangenciar a placa metálica. Um valor
maior de B aumentará a força centrípeta que, por sua vez, reduzirá o raio da trajetória circular. Isto
fará com que o feixe se afaste da placa metálica. Portanto, valores maiores de B, dado por (3)
também são soluções para este problema. Logo:
2mK
B≥
ed
(b) Vetor campo magnético:
2mK
B= k
ed
[Início]
22. A Fig. 32 mostra um dispositivo usado para medir as massas dos íons. Um íon de massa m e
carga +q é produzido basicamente em repouso pela fonte S, a partir de uma descarga através do
gás no interior de uma câmara. O íon é acelerado por uma diferença de potencial V e penetra um
campo magnético B. Ele se move no interior do campo em semicírculo, colidindo com uma
chapa fotográfica a uma distância x da fenda de entrada. Mostre que a massa m do íon é dada
por
B2q 2
m= x .,
8V
(Pág. 150)
Solução.
Aceleração do íon em direção à câmara:
v 2 = v0 + 2ad
2
(1)
Onde v0 é zero, pois o íon parte do repouso. Mas:
V
q
Fe qE qV
a= = = d = (2)
m m m md
Substituindo-se (2) em (1):
________________________________________________________________________________________________________ 3
a
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996. Cap. 34 - O Campo Magnético

4. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
qV 2qV
v2 = 2 d= (3)
md m
Movimento circular no interior da câmara:
Fc = B
mv 2 mv 2 2mv 2
= = = qvB
r x x
2
qB
m= x
2v
q2 B2 2
m2 = x (4)
4v 2
Substituindo-se (3) em (4):
q2 B2 2
m2 = x
2qV
4
m
qB 2 2
m= x
8V
[Início]
39. Uma tira de metal de 6,5 cm de comprimento por 0,88 cm de largura e 0,76 mm de espessura se
desloca, com velocidade constante v, por um campo magnético B = 1,2 mT perpendicular à tira,
conforme ilustra a Fig. 34. Uma diferença de potencial de 3,9 μV é medida entre os pontos x e
y. Calcule a velocidade escalar v.
(Pág. 152)
Solução.
A ação do campo magnético (B) sobre os elétrons de condução da tira de metal resulta numa força
magnética (Fm) sobre os mesmos, dada por:
Fm = qv × B
Pela regra da mão direita, Fm tem sentido apontando de x para y, ao longo da largura da fita
(lembre-se que elétrons têm carga negativa, que deve ser levado em conta na equação acima). O
acúmulo de elétrons do lado direito da tira de metal gera um campo elétrico (E)cuja força (Fe) sobre
os elétrons, no equilíbrio, deve ser igual à força magnética.
________________________________________________________________________________________________________ 4
a
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996. Cap. 34 - O Campo Magnético

5. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
Fe +Fm = 0
qE + qv × B = 0
E = −v × B
Módulo do campo elétrico:
V
E = = vB
d
Logo:
V
v=
Bd
3,9×10-6 V
v= = 0,3693 m/s
(1,2×10-3T).(8,8×10-3m)
v ≈ 37 cm/s
[Início]
42. Um fio de metal de massa m desliza, sem atrito, sobre dois trilhos horizontais separados por
uma distância d, conforme vemos na Fig. 36. Os trilhos estão num campo magnético uniforme
vertical B. Uma corrente constante i, fornecida por um gerador G, passa de um trilho para o
outro através do fio de metal, retornando ao gerador. Determine a velocidade (módulo e sentido)
do fio em função do tempo, supondo que em t = 0 ele está em repouso.
z
x y
(Pág. 152)
Solução.
Força sobre o fio:
F = il × B
F = i ( di ) × ( Bk )
F = −idBj
Aceleração do fio:
F −idB
a= = j
m m
Velocidade do fio em função do tempo:
v = v 0 + at
⎛ −idB ⎞
v = 0+⎜ j⎟ t
⎝ m ⎠
idBt
v=− j
m
________________________________________________________________________________________________________ 5
a
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996. Cap. 34 - O Campo Magnético

6. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
Obs.: Neste cálculo foi desprezada a fem induzida devido à variação do fluxo do campo magnético
através do circuito, que é provocada pelo movimento do fio. A fem induzida tem sinal contrário à
fem do gerador, o que provoca a atenuação da corrente no circuito. O resultado disso é a diminuição
da intensidade da força sobre o fio, com as conseqüentes alterações na aceleração e na velocidade
do fio.
[Início]
46. Um bastão de cobre de 1,15 kg repousa sobre dois trilhos horizontais, separados de 95,0 cm, e
conduz uma corrente de 53,2 A de um trilho para o outro. O coeficiente de atrito estático é 0,58.
Determine o menor campo magnético (não necessariamente vertical) que seria capaz de fazer o
bastão deslizar.
(Pág. 152)
Solução.
Considere o esquema abaixo:
z
y
N x
i Fm
i Fa P
i
l
Para que a barra horizontal deslize, a força magnética deve ser maior do que a força de atrito
estático máxima. No limiar do movimento, teremos:
Fa + Fm = 0
Força de atrito estático sobre o bastão:
Fa = − μe mgj
Logo:
Fm = −Fa = μe mgj (1)
Força magnética sobre a barra:
F = il × B (2)
Onde:
l = li (3)
Extraindo-se B de (2):
il × Fm
B=− 2
(4)
il
Substituindo-se (1) e (3) em (4)
B=−
( ili ) × ( μe mgj)
( il )
2
il μ e mg
B=− k
( il )
2
μ e mg
B=− k
il
________________________________________________________________________________________________________ 6
a
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996. Cap. 34 - O Campo Magnético

7. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
B = 0,12946 T
B ≈ 0,13 T
[Início]
50. O raio da face de um relógio de parede circular tem 15 cm. Em volta dessa face são enroladas
seis voltas de fio, que conduz uma corrente de 2,0 A no sentido horário. O relógio está dentro de
um campo magnético uniforme, constante, de 70 mT (mas continua funcionando perfeitamente).
Exatamente às 13:00 h, o ponteiro das horas aponta no sentido do campo magnético externo. (a)
Depois de quantos minutos o ponteiro dos minutos apontará no sentido do torque provocado
pelo campo magnético sobre o enrolamento? (b) Qual o módulo desse torque?
(Pág. 153)
Solução.
(a) Considere o esquema abaixo:
12 1
B
y θ 2
R 3
z x μ x
i
O enunciado do problema nos revela que o vetor campo magnético aponta para o marcador “1” do
relógio e, portanto, faz um ângulo de θ = 60o com a horizontal. Vetor campo magnético:
B = B cos θ i + B sen θ j
Momento magnético das espiras (direção e sentido segundo a regra da mão direita):
μ = − NiAk
Torque do campo magnético sobre o enrolamento:
τ = μ×B
τ = ( − NiAk ) × ( B cosθ i + B sen θ j)
τ = NiAB ( sen θ i − cosθ j)
Considerando-se que θ = 60o, percebe-se que τ aponta para a marca “4” do relógio (veja esquema
abaixo). Logo, serão necessários 20 min para que o ponteiro dos minutos atinja esta direção.
12 1
2
3
τ
4
(b)
τ = 0, 05937 N.m
τ ≈ 0, 059 N.m
[Início]
________________________________________________________________________________________________________ 7
a
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996. Cap. 34 - O Campo Magnético

8. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
51. Um fio de comprimento L conduz uma corrente i. Mostre que se o fio forma uma bobina
circular, o torque máximo desenvolvido por um determinado campo magnético acontece quando
a bobina tem apenas uma espira e seu módulo é dado por
1 2
τ= L iB .
4π
(Pág. 153)
Solução.
Como o comprimento do fio é fixo, quanto maior o número de espiras menor será a área de cada
uma. O comprimento do fio (L) deve ser igual ao número de voltas (N) vezes o comprimento de
cada volta (2πr).
L = 2π rN
L
r= (1)
2π N
Torque da força magnética sobre a espira:
τ = μ×B
τ = NiABsenθ
τ = Ni (π r 2 ) Bsenθ
Naturalmente o ângulo θ deverá ser igual a π/2 para maximizar o torque:
τ = π Nir 2 B (2)
Substituindo-se (1) em (2):
2
⎛ L ⎞
τ = π Ni ⎜ ⎟ B
⎝ 2π N ⎠
iL2 B
τ=
4π N
Como τ ∝ 1/N, conclui-se que para maximizar o torque o número de espiras deverá ser igual a 1 (N
= 1).
iL2 B
τ=
4π
[Início]
53. A Fig. 40 mostra um fio em anel de raio a, perpendicular à direção de um campo magnético
divergente, radialmente simétrico. O campo magnético tem a mesma intensidade B em todos os
pontos do anel, e seu sentido faz um ângulo θ com a normal ao plano do anel em todos os
pontos. A ponta torcida do fio não têm nenhum efeito sobre o problema. Se o anel conduz uma
corrente i, determine o módulo e o sentido da força que o campo exerce sobre ele, conforme
mostrado na figura.
________________________________________________________________________________________________________ 8
a
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996. Cap. 34 - O Campo Magnético

9. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
(Pág. 153)
Solução.
Vista lateral do sistema:
y
B
dF θ
z x
dl
Força sobre um elemento de fio dl:
dF = idl × B
dF = idlB (1)
Força total sobre o anel:
dF = dFx i + dFy j + dFz k
F = ∫ dFx i + ∫ dFy j + ∫ dFz k
As duas primeiras integrais são nulas devido à simetria envolvida no problema.
F = ∫ dFsenθ k (2)
Substituindo-se (1) em (2):
F = ∫ idlBsenθ k = iBsenθ ( ∫ dl ) k
0
2π a
F = 2π aiBsenθ k
[Início]
55. A Fig. 41 mostra um cilindro de madeira com massa m = 262 g e comprimento L = 12,7 cm,
com um fio enrolado longitudinalmente em volta dele, de maneira que o plano do enrolamento,
com N = 13 voltas, contém o eixo do cilindro e é paralelo a um plano que tem uma inclinação θ
com a horizontal. O cilindro está sobre esse plano inclinado, e o conjunto está sendo submetido
a um campo magnético uniforme, vertical, de 477 mT. Qual a menor corrente que deve circular
no enrolamento, de forma a evitar que o cilindro role para baixo?
________________________________________________________________________________________________________ 9
a
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996. Cap. 34 - O Campo Magnético

10. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
(Pág. 153)
Solução.
Para que o cilindro não role rampa abaixo ou acima, o torque resultante em relação ao centro de
massa, ou em relação ao ponto de contato do cilindro com a rampa, deve ser zero. Em relação ao
centro de massa do cilindro agem os torques devido à força magnética e à força de atrito estático.
Note que nem a força peso nem a normal exercem torques em relação ao centro de massa. No
esquema de forças abaixo, foram omitidas as duas forças magnéticas em z, que agem sobre os lados
das espiras paralelos à pagina.
τm + τa = 0 (1)
Torque da força magnética:
τ m = μ × B = NiABsenθ k (2)
Torque da força de atrito:
τ a = ra × Fa (3)
O cálculo da força de atrito pode ser feito pelas componentes das forças em x e y. Forças em x:
N x − Fax = 0
Nsenθ − Fa cos θ = 0
Fa cos θ
N=
senθ (4)
Forças em y:
N y + Fay − P = 0
Ncosθ + Fa senθ = mg (5)
________________________________________________________________________________________________________ 10
a
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996. Cap. 34 - O Campo Magnético

11. Problemas Resolvidos de Física Prof. Anderson Coser Gaudio – Depto. Física – UFES
Substituindo-se (4) em (5):
Fa cos θ
cosθ + Fa senθ = mg
senθ
⎛ cos 2 θ + sen 2θ ⎞
Fa ⎜ ⎟ = mg
⎝ senθ ⎠
Fa = mgsenθ (6)
Pode-se agora resolver (3):
τ a = −rmgsenθ k (7)
Substituindo-se (2) e (7) em (1):
NiAB sen θ k − rmg sen θ k = 0
Ni (2rL ) B = rmg
2NiLB = mg
mg
i=
2 NLB
i = 1, 6318 A
i ≈ 1, 63 A
[Início]
________________________________________________________________________________________________________ 11
a
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996. Cap. 34 - O Campo Magnético