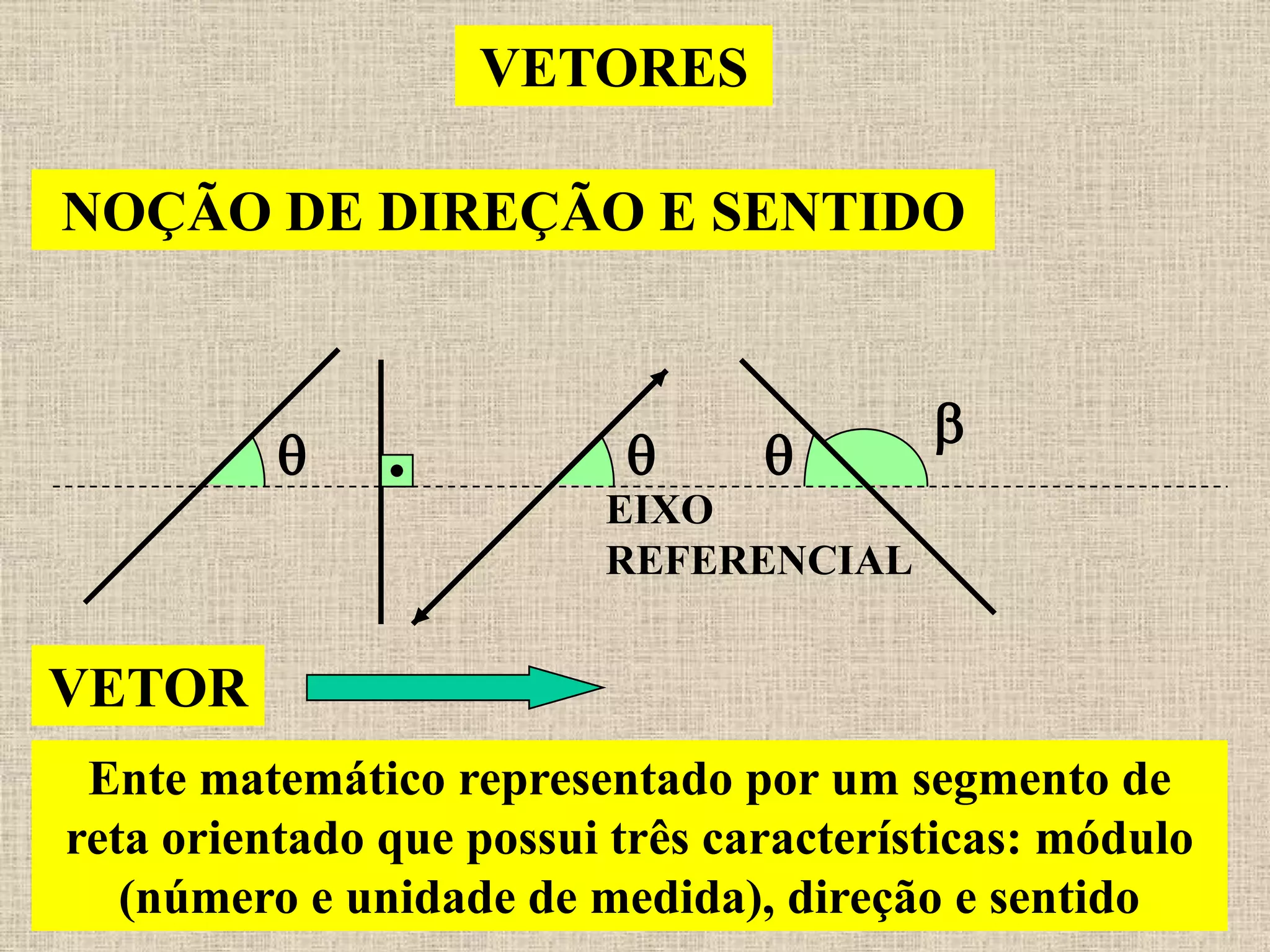
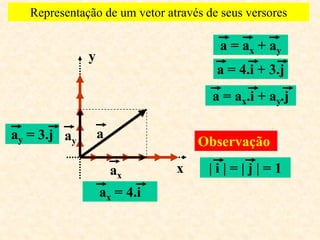
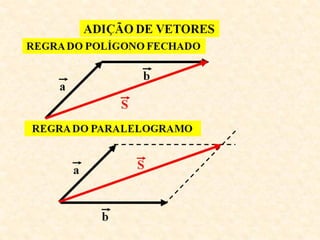
1) O documento discute vetores, incluindo suas características de módulo, direção e sentido. 2) A soma e subtração de vetores são explicadas usando a regra do paralelogramo e a adição e subtração de componentes. 3) A multiplicação de um vetor por um número real é definida em termos de módulo, direção e sentido.

1. 



VETORES
NOÇÃO DE DIREÇÃO E SENTIDO
EIXO REFERENCIAL
VETOR
Ente matemático representado por um segmento de reta orientado que possui três características: módulo (número e unidade de medida), direção e sentido

3. 
Soma de dois vetores –Regra do Paralelogramo

b
a
S
S
a
b
= +
S2= a2+ b2+ 2abcos
x
y
a
S2= (b + y)2+ x2
S2= b2+ 2by + y2+ x2
Observe que:
cos =
y
a
a.cos 
y =
S2= b2+ 2bacos + a2
S2= a2+ b2+ 2abcos
a2

4. 
SUBTRAÇÃO VETORIAL
a
b
S
S
a
b
= +
a
b
–= ?
D
a + (-b) = D
–b
D
D

a
b
D
= –
a
b

a
b
D’
= –
b
a
a –b 
b –a
D
D’

D
D’
=
a –b =
b –a

5. 
Subtração de vetores
a
b
a + (-b) = D
–b
D
D2= a2+ b2+ 2abcos(180 -)
180º -
Lembre que cos 120º = -½ e cos 60º = ½
Ou seja, que cos 120º = -cos 60º
cos (180º -60º) = -cos 60º
cos(180º -) = -cos 
D2= a2+ b2+ 2abcos(180 -)
D2= a2+ b2-2abcos

6. Produto de um Número Real por um Vetor
Seja um vetor abaixo e um número real n:
a
n.a = p
Módulo:
|p| = |n|.|a|
Direção:
2N
a mesma de a
Se n > 0, mesmo de a
Se n < 0, contrário ao de a
Exemplos:
x 3 =
2N
x -2 =
6 N
-4 N
Sentido:

8. 
Decomposição de um vetor em componentes ortogonais
a
x
y
ax
ay
ay
cos =
ax
a

ax= a.cos 
sen =
ay
a

ay= a.sen 
Observação
a2= ax2+ ay2

9. Representação de um vetor através de seus versores
x
y
a
ax
ay
a = ax+ ay
ax= 4.i
ay= 3.j
a = 4.i + 3.j
a = ax.i + ay.j
Observação
| i | = | j | = 1