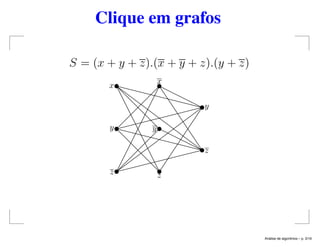
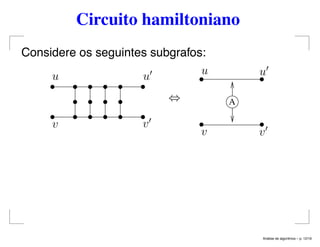
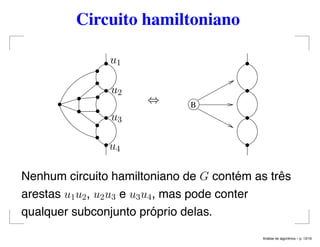
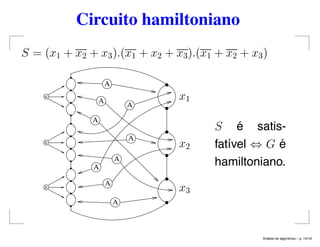
O documento aborda a análise de algoritmos e a NP-completude, focando principalmente em problemas envolvendo grafos, como o problema do clique, isomorfismo de subgrafos e circuito hamiltoniano. Estabelece teoremas que provam que vários problemas são NP-completos e apresenta exercícios relacionados a esses conceitos. O texto explora também questões sobre conjuntos independentes, cobertura por vértices e problemas de particionamento, configurando um panorama abrangente sobre a complexidade computacional na teoria dos grafos.

1. Análise de algoritmos
Mais problemas NP-completos
An´alise de algoritmos – p. 1/19

2. Clique em grafos
Clique: Dado um grafo G e um inteiro K, G tem um
subgrafo completo (clique) de tamanho ≥ K?
An´alise de algoritmos – p. 2/19

3. Clique em grafos
Clique: Dado um grafo G e um inteiro K, G tem um
subgrafo completo (clique) de tamanho ≥ K?
Teorema: Clique é NP-completo.
An´alise de algoritmos – p. 2/19

4. Clique em grafos
Clique: Dado um grafo G e um inteiro K, G tem um
subgrafo completo (clique) de tamanho ≥ K?
Teorema: Clique é NP-completo.
Clique ∈ NP (
√
)
An´alise de algoritmos – p. 2/19

5. Clique em grafos
Clique: Dado um grafo G e um inteiro K, G tem um
subgrafo completo (clique) de tamanho ≥ K?
Teorema: Clique é NP-completo.
Clique ∈ NP (
√
)
SAT clique
An´alise de algoritmos – p. 2/19

6. Clique em grafos
Clique: Dado um grafo G e um inteiro K, G tem um
subgrafo completo (clique) de tamanho ≥ K?
Teorema: Clique é NP-completo.
Clique ∈ NP (
√
)
SAT clique
Dado uma instância S do SAT com K cláusulas,
vamos construir um grafo G tal que G tem uma
clique de tamanho K ⇔ S é satisfatível.
An´alise de algoritmos – p. 2/19

7. Clique em grafos
S = (x + y + z).(x + y + z).(y + z)
An´alise de algoritmos – p. 3/19

8. Clique em grafos
S = (x + y + z).(x + y + z).(y + z)
x
y
z
x
y
z
y
z
An´alise de algoritmos – p. 3/19

9. Exercícios
1. Construa um grafo G tal que G tem uma clique
de tamanho 4 se e somente se a fórmula
S = (x1+x2+x3).(x1+x2+x3).(x1+x2+x3).(x1+x2+x3)
é satisfatível.
An´alise de algoritmos – p. 4/19

10. Exercícios
2. Considere o seguinte algoritmo para resolver o
problema clique:
para cada S ⊆ V com k vértices, verifique se
S é uma clique.
O algoritmo acima tem complexidade O(nk
).
Logo, ele é polinomial. O que está errado?
An´alise de algoritmos – p. 5/19

11. Exercícios
3. Mostre que Isomorfismo de Subgrafos (Dados
dois grafos G1 e G2, G1 é subgrafo de G2?) é
NP-completo. (Sugestão: Use o clique).
An´alise de algoritmos – p. 6/19

12. Mais problemas NP-completos
Conjunto independente: Dado um grafo G e um
inteiro k, existe um subconjunto I com k vértices
tal que nenhuma aresta liga dois vértices de I?
An´alise de algoritmos – p. 7/19

13. Mais problemas NP-completos
Conjunto independente: Dado um grafo G e um
inteiro k, existe um subconjunto I com k vértices
tal que nenhuma aresta liga dois vértices de I?
Cobertura por v´ertices: Dado um grafo G e um inteiro
k, existe um subconjunto C com k vértices tal que
cada aresta de G é incidente a algum vértice de C?
An´alise de algoritmos – p. 7/19

14. Mais problemas NP-completos
Teorema: Dado um grafo G = (V, E) e um
subconjunto S ⊆ V , as seguintes afirmações são
equivalentes:
S é uma clique de G
S é um conjunto independente de G
V − S é uma cobertura por vértices de G
OBS: G é o grafo complementar de G.
An´alise de algoritmos – p. 8/19

15. Mais problemas NP-completos
Corol´ario: Os problemas do conjunto independente
e cobertura por vértices são NP-completos.
An´alise de algoritmos – p. 9/19

16. Exercícios
1. Mostre que o problema da cobertura por
vértices permanece NP-completo mesmo se
todos os vértices do grafo tiverem grau par.
(Sugestão : use o problema original).
2. O que acontece com o problema da cobertura
por vértices se o grafo for uma árvore?
An´alise de algoritmos – p. 10/19

17. Circuito hamiltoniano
Circuito hamiltoniano: Um dado grafo G é
hamiltoniano?
An´alise de algoritmos – p. 11/19

18. Circuito hamiltoniano
Circuito hamiltoniano: Um dado grafo G é
hamiltoniano?
Teorema: Circuito hamiltoniano é NP-completo.
An´alise de algoritmos – p. 11/19

19. Circuito hamiltoniano
Circuito hamiltoniano: Um dado grafo G é
hamiltoniano?
Teorema: Circuito hamiltoniano é NP-completo.
Circuito hamiltoniano ∈ NP. (
√
)
An´alise de algoritmos – p. 11/19

20. Circuito hamiltoniano
Circuito hamiltoniano: Um dado grafo G é
hamiltoniano?
Teorema: Circuito hamiltoniano é NP-completo.
Circuito hamiltoniano ∈ NP. (
√
)
3-SAT circuito hamiltoniano.
An´alise de algoritmos – p. 11/19

21. Circuito hamiltoniano
Considere os seguintes subgrafos:
A
u uu u
v
v v
v
⇔
An´alise de algoritmos – p. 12/19

22. Circuito hamiltoniano
B
u1
u2
u3
u4
⇔
Nenhum circuito hamiltoniano de G contém as três
arestas u1u2, u2u3 e u3u4, mas pode conter
qualquer subconjunto próprio delas.
An´alise de algoritmos – p. 13/19

23. Circuito hamiltoniano
S = (x1 + x2 + x3).(x1 + x2 + x3).(x1 + x2 + x3)
B
B
B
A
A
A
A
A
A
A
A
A
x1
x2
x3
S é satis-
fatível ⇔ G é
hamiltoniano.
An´alise de algoritmos – p. 14/19

24. Exercícios
1. Um caminho hamiltoniano é um caminho que contém
todos os vértices de um grafo. Mostre que o problema
de decidir se um dado grafo contém um caminho
hamiltoniano é NP-completo.
(Sugestão: use o circuito hamiltoniano.)
2. Mostre que os seguintes problemas são
NP-completos: Dado um grafo G = (V, E), um conjunto
L ⊆ V , e um inteiro k, existe uma árvore geradora T de
G tal que
(a) O conjunto das folhas de T é L?
(b) T tem k folhas?
(c) Os vértices de T têm grau máximo k?
(Sugestão: Use o problema do caminho hamiltoniano.)
An´alise de algoritmos – p. 15/19

25. Exercícios
Considere o seguinte problema:
Partição: dado um conjunto S de inteiros, os elementos de
S podem ser particionados em dois subconjuntos A e
A = S − A tal que x∈A x = x∈A x?
3. Sabendo que o problema da partição é NP-completo,
mostre que o problema abaixo também é
NP-completo:
Dados m máquinas idênticas, n tarefas com duração
t1, t2, . . . , tn (onde cada ti é um inteiro positivo) para
serem executadas pelas máquinas, e um inteiro
positivo T. Existe uma distribuição das tarefas pelas
máquinas tal que o tempo total de execução é
menor ou igual a T?
An´alise de algoritmos – p. 16/19

26. Exercícios
4. Sabendo que o problema da partição é NP-completo,
mostre que o problema abaixo também é
NP-completo:
Mochila 0-1: Dado um conjunto U = {u1, u2, . . . , un},
valores inteiros positivos wi e ci (respectivamente, o
peso e o custo) associados a cada elemento ui de
U, e dois inteiros positivos W e C. Deseja-se saber
se existe um subconjunto S de U tal que
ui∈S wi ≤ W e ui∈S ci ≥ C?
An´alise de algoritmos – p. 17/19

27. Exercícios
5. Considere a seguinte versão do problema do caminho
mínimo: dado um grafo G, possivelmente com arestas
de peso negativo, vértices s e t e um inteiro k, decidir
se existe um caminho de s a t de peso menor ou igual a
k. Mostre que este problema é NP-completo.
(Sugestão: use o circuito hamiltoniano.)
An´alise de algoritmos – p. 18/19

28. Exercícios
6. Mostre que o problema abaixo é NP-completo:
(Hitting set): dados um conjunto universo T e:
uma coleção {S1, S2, . . . , Sn}, onde cada Si ⊆ T e;
um inteiro positivo k ≤ |T|.
O problema é determinar se existe um subconjunto
H de T tal que |H| ≤ k e ∀i ∈ {1, 2, ..., n},
(H ∩ Si) = ∅.
7. Um grafo é chamado de caterpillar se ele possui um
caminho C tal que todas as suas folhas distam 1 de C.
Mostre que o problema de decidir se um dado grafo é
caterpillar é NP-completo.
An´alise de algoritmos – p. 19/19