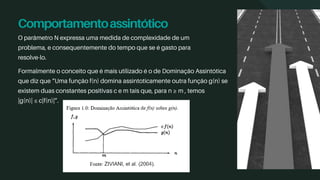
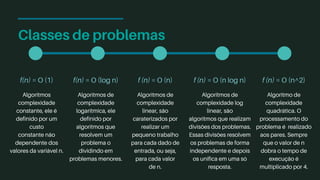
O documento aborda a análise de complexidade em algoritmos, destacando a importância de comparar a eficiência de diferentes algoritmos em função de suas instruções em cenários de pior e melhor caso. Apresenta conceitos como dominação assintótica e diferentes notações (o, ω, θ) que descrevem limites de complexidade, além de classificar algoritmos conforme suas complexidades (constante, logarítmica, linear, log-linear, quadrática, cúbica e exponencial). A análise matemática é fundamental para prever o desempenho dos algoritmos em diferentes condições.

1. Lucas Bernardo de Souza Nascimento
Análise
de Complexidade em
Algoritmos

2. Introdução
Ela é importante porque torna possível implementar
analisar fatores que não são possíveis empiricamente,
como a comparação entre vários algoritmos que
realizam uma determinada tarefa, ou a previsão de um
comportamento ou do seu provável custo quando
mudado algum parâmetro, ou para um novo ambiente.
A IMPORTÂNCIA DA ANÁLISE
MATEMÁTICA

3. Contando Instruções
Podemos analisar o
número de instruções
segundo alguns cenários
esperados, como no pior
caso onde executa o
número
máximo de instruções e no
melhor caso onde se
executa o número mínimo
de instruções.
Deste modo para analise de
complexidade do
algoritmo mais comumente
usada, se utiliza o número
de instruções no pior caso,
porque esse é ser o caso
onde é possível cobrir todas
as possibilidades e
comparar os algoritmos em
valores de n grandes.

4. Comportamentoassintótico
O parâmetro N expressa uma medida de complexidade de um
problema, e consequentemente do tempo que se é gasto para
resolve-lo.
Formalmente o conceito que é mais utilizado é o de Dominação Assintótica
que diz que “Uma função f(n) domina assintoticamente outra função g(n) se
existem duas constantes positivas c e m tais que, para n ≥ m , temos
|g(n)| ≤ c|f(n)|”.

5. Tipos de análise assintótica
NOTAÇÃO O
Formalmente é definida como
g(n) = O(f(n)), onde isso
significa que f(n) domina
assintoticamente g(n). Ela
descreve o limite assintótico
superior, e é utilizada para
analisar o “pior caso” do
determinado algoritmo.
NOTAÇÃO Ω
Uma função g(n) é Ω(f(n)) se g(n)
domina assintoticamente f(n). A
notação Ômega define o limite
inferior. Desta maneira a notação
Ômega permite demonstrar o
valor do limite inferior da função
complexidade. E assim é utilizada
para analisar o “melhor caso” do
algoritmo.
NOTAÇÃO Θ
Essa notação é utilizada na
definição do chamado limite
assintótico firme. Ela analisa
simultaneamente o limite
inferior e superior desse
algoritmo. Então a definição
formal é que uma função g(n) é
Θ(f(n)) se g(n) e f(n) dominam
assintoticamente uma à outra.

6. Classes de problemas
f(n) = O (1)
Algoritmos
complexidade
constante, ele é
definido por um
custo
constante não
dependente dos
valores da variável n.
f(n) = O (log n)
Algoritmos de
complexidade
logarítmica, ele
definido por
algoritmos que
resolvem um
problema o
dividindo em
problemas menores.
f (n) = O (n)
Algoritmos de
complexidade
linear, são
caraterizados por
realizar um
pequeno trabalho
para cada dado de
entrada, ou seja,
para cada valor
de n.
f (n) = O (n log n)
Algoritmos de
complexidade log
linear, são
algoritmos que realizam
divisões dos problemas.
Essas divisões resolvem
os problemas de forma
independente e depois
os unifica em uma só
resposta.
f (n) = O (n^2)
Algoritmo de
complexidade
quadrática. O
processamento do
problema é realizado
aos pares. Sempre
que o valor de n
dobra o tempo de
execução é
multiplicado por 4.

7. Classes de problemas
f (n) = O (n^3)
Definido
como um algoritmo de
complexidade cúbica. Mesmo
para um n não muito grande esta
classe de competividade já é
muito custosa. Quando o valor
de n é 100, o número
de operações é da já é da ordem
de 1 milhão.
ƒ(n) = O (2^n)
Chamado de algoritmo de
complexidade exponencial.
Não são
uteis de forma prática,
porque mesmo para valores
de n relativamente
pequenos o
número de operações já
passada dos milhões.

8. CONSIDERAÇÕES
FINAIS E OBRIGADO!
CONCLUSÃO