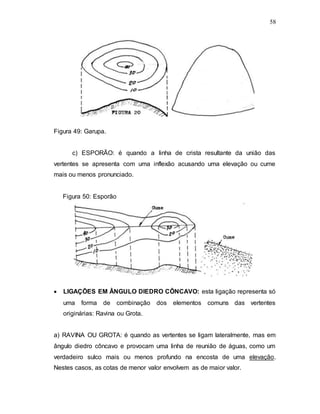
1) O documento discute a evolução histórica da topografia e cartografia, desde os primeiros deslocamentos humanos até os avanços científicos e tecnológicos modernos. 2) A topografia é definida como o estudo dos métodos e instrumentos para medir e representar graficamente parte da superfície terrestre, enquanto a cartografia é a ciência, técnica e arte de mapear a terra. 3) A topografia se divide em topometria, topologia, taqueometria e fotograme

1. UNIVERSIDADE DA AMAZÔNIA
CENTRO DE CIÊNCIAS EXATAS E NATURAIS
CURSO: ENGENHARIA CIVIL
A
AP
PO
OS
ST
TI
IL
LA
A D
DE
E T
TO
OP
PO
OG
GR
RA
AF
FI
IA
A
Belém-PA
2014

2. 2
Unidade I – INTRODUÇÃO À TOPOGRAFIA
1.1 – HISTÓRICO DA EVOLUÇÃO DA TOPOGRAFIA E DA CARTOGRAFIA
Mesmo considerando todos os avanços científicos e tecnológicos
produzidos pelo homem através dos tempos, é possível, nos dias de hoje,
entender a condição de perplexidade dos ancestrais, no começo dos dias, diante
da complexidade do mundo a sua volta. Pode-se também intuir de que maneira
surgiu no homem a necessidade de conhecer o mundo que ele habitava.
O simples deslocamento de um ponto a outro na superfície de nosso
planeta, já justifica a necessidade de se visualizar de alguma forma as
características físicas do "mundo". É fácil imaginar alguns dos questionamentos
que surgiram nas mentes desses ancestrais, por exemplo: como orientar os seus
deslocamentos? Qual a forma do planeta? etc..
A topografia cujo significado etimológico da palavra é “descrição do lugar”,
estuda os instrumentos, métodos de operação no terreno, cálculo e desenhos
necessários ao levantamento e representação gráfica mais ou menos detalhada
de uma parte da superfície terrestre.
Os egípcios, os gregos, os árabes e os romanos legaram instrumentos e
processos que, embora primitivos, serviram para descrever a história da
topografia, onde são mencionadas plantas e cartas militares e geográficas bem
interessantes, organizadas nos primórdios da topografia, ou melhor, da chamada
Geometria Aplicada.
Entretanto, somente nos últimos séculos, a topografia teve uma orientação
orgânica, passando do empirismo às bases de uma autêntica ciência, graças ao
desenvolvimento notável que tiveram especialmente a Matemática e a Física.
Os aperfeiçoamentos da mecânica de precisão introduzidos nos
instrumentos topográficos devem-se principalmente aos geniais estudos do
engenheiro suíço Henrique Wild, do geodesista italiano Ignazio Porro, do Carl
Zeiss, e tantos outros que contribuíram eficientemente para o progresso crescente
da aplicação dos métodos desenvolvidos pela topografia, principalmente no
extraordinário aperfeiçoamento da fotogrametria terrestre e aérea, esta última

3. 3
dominando hoje em dia a maioria dos grandes levantamentos topográficos, pela
exatidão, presteza e custo mais reduzido dos trabalhos.
Amssler, Coradi, Galileu e muitos outros, deram a topografia o valor que
realmente tem como ciência e como técnica no levantamento topométrico preciso
do terreno e na representação gráfica equivalente, servindo como apoio de
qualquer trabalho de engenharia.
Já o conceito de Cartografia tem suas origens intimamente ligadas às
inquietações que sempre se manifestaram no ser humano, no tocante a conhecer
o mundo que ele habitava.
O vocábulo CARTOGRAFIA, etmologicamente significa descrição de cartas
e foi introduzido em 1839, pelo segundo Visconde de Santarém - Manoel
Francisco de Barros e Souza de Mesquita de Macedo Leitão, (1791 - 1856). A
despeito de seu significado etmológico, a sua concepção inicial continha a idéia do
traçado de mapas. No primeiro estágio da evolução o vocábulo passou a significar
a arte do traçado de mapas, para em seguida, conter a ciência, a técnica e a arte
de representar a superfície terrestre.
O conceito da Cartografia, hoje aceito sem maiores contestações, foi
estabelecido em 1966 pela Associação Cartográfica Internacional (ACI), e
posteriormente, ratificado pela UNESCO, no mesmo ano: "A Cartografia
apresenta-se como o conjunto de estudos e operações científicas, técnicas e
artísticas que, tendo por base os resultados de observações diretas ou da análise
de documentação, se voltam para a elaboração de mapas, cartas e outras formas
de expressão ou representação de objetos, elementos, fenômenos e ambientes
físicos e socioeconômicos, bem como a sua utilização."
O processo cartográfico, partindo da coleta de dados, envolve estudo,
análise, composição e representação de observações, de fatos, fenômenos e
dados pertinentes a diversos campos científicos associados a superfície terrestre.
A Geografia e a Geodésia estão intimamente ligadas à topografia e à
cartografia, utilizando as primeiras observações astronômicas dos pontos de suas
cartas, enquanto que os levantamentos geodésicos exigem processos rigorosos
nas medidas, só possíveis com o emprego aparelhos de alta precisão, como um

4. 4
Alta Azimutal de Precisão utilizado no passado, ou Will T3, Zeiss II ou outros no
presente, menores, mais leves, mais precisos e mais cômodos de aplicação.
Desta forma, topografia e cartografia são ciências irmãs que trabalham
articuladas entre si, para ajudar os estudiosos das mais diversas áreas no que
tange à analise da superfície terrestre ou de uma parte dela.
1.2 – DISTINÇÃO ENTRE A TOPOGRAFIA E A GEODÉSIA
A geodésia, com o auxilio da geografia matemática, se ocupa dos
processos da medida e especificação para o levantamento e representação
cartográfica de uma extensão da superfície terrestre, projetada numa superfície de
referência geométrica e analiticamente definida por parâmetros, variável em
número, de acordo com a consideração sobre a forma da terra.
No desenvolvimento do estudo da geodésia, se considera a superfície em
referência como o elipsóide de revolução com parâmetros a e b numericamente
determinados.
A geodésia que determina com precisão as malhas triangulares justapostas
à superfície do elipsóide de revolução terrestre determinando as coordenadas dos
seus vértices é a ciência que abrange o todo.
A topografia se ocupa de detalhes de cada malha ou quadrícula e,
admitindo-a plana, adota processos da Geometria e Trigonometria Planas, com
ligação às coordenadas de referência determinadas, como se diz,
geodesicamente.
1.3 CONCEITOS FUNDAMENTAIS
A topografia tem por finalidade determinar o contorno, dimensão e posição
relativa de uma porção limitada da superfície terrestre, sem levar em consideração
a esfericidade resultante da curvatura da terra.

5. 5
Nestas condições, pode-se sempre, figurar em um plano a imagem da
região considerada, o que equivale a projetar sobre um plano, que se supõe
horizontal, não só os limites da superfície a representar todas as particularidades
notáveis, naturais e artificiais do terreno.
Assim, a topografia é uma ciência aplicada, baseada na geometria e na
trigonometria, de âmbito restrito, pois é um capítulo da geodésia que tem por
objetivo o estudo da forma e dimensões da terra.
A topografia se incumbe da representação, por uma projeção ortogonal
cotada, de todos os detalhes da configuração do solo, mesmo que se trate de
detalhes artificiais: canais, estradas, cidades, vilas e construções isoladas, etc.
Esta projeção se faz sobre uma superfície de nível, isto é, sobre uma
superfície definida propriedade de ser, em cada um de seus pontos, normal à
direção da gravidade: as projetantes dos pontos a representar são, pois verticais
desses pontos.
A esta projeção ou imagem figurada do terreno dá-se o nome de planta ou
plano topográfico, que em geral são representados pela cartografia.
Ao conjunto de métodos empregados para colher os dados necessários
para o traçado da planta dá-se o nome de topometria, que se subdivide em
planimetria e altimetria ou nivelamento.
1. 4 – DIVISÕES DA TOPOGRAFIA
Pode-se subdividir a topografia em quatro partes principais: a topometria, a
topologia, a taqueometria e a fotogrametria.
1.4.1 – Topometria:
É o conjunto de processos empregados para medição de grandezas
lineares e angulares necessárias ao traçado da planta ou perfil. Se sub-dividindo
em Planimetria e Altimetria

6. 6
a) Planimetria:
É a medição de grandezas lineares e grandezas angulares sobre um plano
horizontal. As grandezas lineares são as distâncias horizontais ou ângulos
azimutais, estas grandezas são representadas em planos horizontais e a esta
representação chamamos de planta topográfica.
b) Altimetria:
É a medição de grandezas lineares e grandezas angulares sobre um plano
vertical. As grandezas lineares são distâncias verticais também chamadas de cota
ou diferença de nível, as grandezas angulares são os ângulos verticais ou ângulos
zenitais. Estas grandezas são representadas em planos verticais e a esta
representação chamamos perfil ou corte ou elevação ou ainda vista lateral. A
única representação de altimetria em plano horizontal é constituída pelas curvas
de nível.
1.4.2 – Topologia:
É o estudo das formas exteriores da superfície terrestre e das leis que deve
obedecer ao seu modelado. Sua aplicação principal é na representação
cartográfica do terreno pelas curvas de nível, que são as interseções obtidas por
planos equidistantes paralelos com o terreno a representar.
Na interpretação das referidas curvas, obtidas diretamente ou por
interpolação, pode-se verificar as correções na implantação de pontos, quando
erradamente assinaladas na planta.
1.4.3 – Taqueometria:
É a medição indireta das distâncias. Tendo por finalidade o levantamento
de pontos do terreno, pela resolução de triângulos-retângulos aptos a representa-
los, tanto plani como altimetricamente, ou em outras palavras, dando origem as
plantas cotadas ou com curvas de nível, ditas plani-altimétricas.

7. 7
Sua aplicação principal é em zonas fortemente acidentadas, em morros,
montanhas, onde oferece reais vantagens sobre métodos topométricos, pois o
levantamento dos pontos é feita com rapidez, maior exatidão e economia.
1.4.4 – Fotogrametria:
A fotogrametria é uma parte importante da topografia, que no passado foi
relegada a um plano secundário, e considerada como apêndice desta, é hoje
justamente classificada em primeiro plano, tornando-se o método principal para
determinar o relevo do terreno, principalmente de grandes extensões.
Nos grandes levantamentos, e até mesmo nos menores, não se emprega
tanto os taqueômetros e as réguas ou miras graduadas, chamadas estádias, mas
sim as câmeras fotográficas, isto é, fotogrâmetros ou fototeodolitos e o restituidor
fotogramétrico.
A topografia continua, entretanto, a ser auxiliar indispensável da
fotogrametria, pois serve, para estabelecer a ossatura geométrica do relevo, e por
outro lado, para auxiliar em medidas complementares no terreno de detalhes
encobertos ou tornados invisíveis pela vegetação. As enormes dificuldades
apresentadas nos relevos topográficos de montanhas elevadas são vencidas pela
fotogrametria, tanto que a mesma é empregada em larga escala por todos os
serviços cartográficos do mundo.
A fotogrametria se subdivide em fotogrametria aérea e fotogrametria
terrestre.
a) Fotogrametria aérea:
É a fotografia tomada de avião, de terrenos encobertos pela vegetação e
levemente ondulados.
b) Fotogrametria terrestre:
É a fotografia tomada de pontos elevados de terrenos descobertos de
vegetação e bastante acidentados.

8. 8
1.5– UNIDADE DE MEDIDA UTILIZADAS NA TOPOGRAFIA:
1.5.1 – Conceito:
A porção de uma grandeza tomada como termo de comparação é chamada
Unidade de Medida. O número que exprime quantas vezes certa grandeza é maior
ou menor do que a unidade escolhida denomina-se Medida de Grandeza.
Distingui-se em Topografia, três espécies de grandezas, a saber: lineares,
angulares e superficiais.
Ex1) A B
10x unidades de 1metro
logo, AB = 10m
Ex2) A B
45x unidades de 1grau
logo, AÔB = 45o
45o
O
1.5.2 – Divisão:
a) Unidades de natureza linear:
 metro (submúltiplos), pés, jardas, milhas e polegadas.
b) Unidades de natureza angular:
 Sistema Sexagesimal (grau)
 Sistema Centesimal (grado)
 Milésimo
c) Unidades de superfície:
 metro quadrado (submúltiplos), are, hectare e centiare.

9. 9
OBS) Para volumes usa-se o m3 e excepcionalmente para pequenos
volumes de água (de vazão) usa-se o litro.
Ex) 1m3 = 1.000 l
1.6– APLICAÇÃO DA TOPOGRAFIA E DA CARTOGRAFIA NA ENGENHARIA
CIVIL:
A topografia existe em todas as atividades da Engenharia que necessitem
dela, como um “meio” e não como um “fim”. Pode-se afirmar que ela é aplicada
em todos os trabalhos de Engenharia Civil, em maior ou menor escala.
Para entender o porquê dessas afirmações é necessário saber o que a
Topografia e a Cartografia conseguem fazer e as outras ciências não: medir ou
calcular distâncias horizontais e verticais, calcular ângulos horizontais e verticais
com alta ou altíssima precisão e representa-los graficamente. Quem mais pode
medir distâncias horizontais com erro provável de 1 para 100.000? Quem mais
pode calcular altitudes (cotas) com precisão de um décimo de milímetro? Quem
mais pode medir ângulos horizontais e verticais com precisão de um segundo
sexagesimal? Por isso os métodos e equipamentos topográficos constituem um
recurso para as atividades de Engenharia.
Citar-se-á a seguir alguns exemplos, dentro dos trabalhos de Engenharia
Civil, que usam da Topografia.
 Edificações: A Topografia faz o levantamento plano-altimétrico do
terreno, como dado fundamental ao projeto; após o projeto estar pronto,
faz sua locação e, durante a execução da obra, controla as prumadas,
os níveis e alinhamentos.
 Estradas (rodovias e ferrovias): Participa do “reconhecimento; ajuda no
“anteprojeto”; executa a “linha de ensaio” ou “linha básica”; faz o projeto
do traçado geométrico; loca-o; projeta a terraplenagem; resolve o

10. 10
problema de transporte de terra; controla a execução e pavimentação (a
infraestrutura, no caso das ferrovias); colabora na sinalização, corrige
falhas, tais como curvas mal traçadas, etc
 Barragens: A Topografia faz os levantamentos plano-altimétricos para o
projeto, loca-o, determina o contorno da área inundada; controla a
execução sempre nos problemas de prumadas, níveis e alinhamentos;
 Áreas degradadas: Nesse contexto, a topografia, ocupando posição
primordial na Engenharia, deve ser um item indispensável à tomada de
decisões para a realização de um Licenciamento Ambiental para
Recuperação de Áreas Degradadas, haja vista o que determina a
Instrução Normativa IN-16 da Fundação do Meio Ambiente (Fatma): no
processo de Licenciamento Ambiental para a Recuperação de Áreas
Degradadas, deverá ser apresentada a planta planialtimétrica da área
do plano ou projeto, com hidrografia, Áreas de Preservação Permanente
(APP) e detalhe do plano/projeto, em UTM ou coordenada geográfica
com a informação do Datum de origem (FUNDAÇÃO DO MEIO
AMBIENTE, 2007). Para tanto, a topografia necessita fazer um
levantamento do processo de degradação das áreas exploradas, em
especial, por processos de erosão, exploração mineral, mapear este
processo e registra-lo.
 Drenagem – em todas as obras de drenagem são necessários os
levantamentos topográficos do terreno para identificar em que cota ou
altura o mesmo se encontra, pois esta pode interferir nas atividades de
escavação e contenção.
A Topografia é utilizada também em trabalhos de saneamento, água,
esgoto; construção de pontes, viadutos, túneis, portos, canais, irrigação,
arruamentos e loteamentos, porém sempre como um “meio” para atingir uma outra
finalidade.

11. 11
1.7– FORMA E DIMENSÕES DA TERRA:
A forma da Terra, ainda não possui uma definição matemática rigorosa,
mesmo porque ela varia na época das chuvas e das secas e sofre constantes
modificações devido à ação de agentes químicos e mecânicos e devido à ação
de agentes internos e externos.
A superfície física da Terra é bastante irregular. Ela é constituída por
elevações e depressões relativamente pequenas, quando comparadas às
dimensões do planeta (R = 6.378.000m ou 6378Km). Elas alcançam um máximo
de aproximadamente 1/10000 do raio terrestre.
Podem ser atribuídas a Terra, cinco formas:
 Real;
 Esférica;
 Plana;
 Elipsoidal; e
 Geoidal.
Apresentar-se-á a seguir, uma breve descrição das diferentes formas da
Terra encontradas nas bibliografias.
1.7.1 – Real: é a verdadeira forma da Terra, que ainda não está definida
matematicamente. Considera-se nesse caso, o relevo e todas as suas
irregularidades de forma. Além disso, conforme afirmação anterior, a Terra não é
estável, sofrendo modificações devido a agentes exteriores e interiores, que
modificam sua forma constantemente. Para os propósitos da Engenharia,
entretanto, essas pequenas modificações podem ser desprezadas e a Terra é
considerada como tendo uma forma estável.
1.7.2 – Esférica: é a forma geométrica aproximada da superfície terrestre que
substitui a forma real por uma esfera. Esta é a aproximação mais simples, mas

12. 12
que ainda permite alcançar bons resultados em muitas aplicações da Engenharia
e da Astronomia.
1.7.3 – Plana: é a forma geométrica simplificada da Terra, que a considera como
um plano. Este artifício restringe-se a aplicações específicas da Mensuração.
1.7.4 – Elipsoidal: é a forma geométrica aproximada da Terra que substitui a real
por um elipsóide de revolução. Esta é a aproximação atualmente adotada na
Geodésia e sobre a qual estão desenvolvidas todas as suas teorias. O elipsóide é
gerado a partir da rotação de uma elipse em torno do eixo de rotação terrestre
(coincidente com a linha dos pólos). Essa forma é a que melhor se adapta ao
geóide.
1.7.5 – Geoidal: é a forma geométrica da Terra definida pela superfície
equipotencial dos mares, suposta em equilíbrio, e prolongada sob os continentes
formando uma superfície fechada. O geóide é a superfície tomada como
referência para as medições altimétricas (altitudes ortométricas).
1.8 – ERRO PLANIMÉTRICO:
Na Geodésia a superfície de referência para medidas planimétricas é a
curva, ao passo que na Topografia é plana, razão por que se deve avaliar a
extensão máxima dos levantamentos topográficos.
Assim, seja, com efeito a Figura 01, temos:

13. 13
Figura 01: Erro Planimétrico
M e P → 2 pontos da superfície física
m e p → projeções ortogonais de M e P sobre a calota esférica
O → centro da terra
 → ângulo central
p’ → projeção cônica de P sobre a tangente T
mp” = mp’
D → erro de esfericidade absoluta
D = D’ – D
D’ = mp’ = R. tg 
D = mp = R  (expresso em radianos)
1.8.1– Erro de Esfericidade Absoluto:
D = D’ – D D = R ³/3
D = R.tg – R  = D/R
D = R (tg – ) ³ = D³/R³
tg =  + ³/3 D = (R/3) . (D³/R³)
D = R ( + ³/3 - ) D = D³/ 2R³

14. 14
1.8.2– Erro de Esfericidade Relativo:
D’ – D = D = (D³/3R²)
D D D
D³/3D² x 1/D  D = D²/3R²
Assim, para pequenos ângulos temos:
 D' (m) D (m)
Erro de Esfericidade
Absoluto (D)Relativo (D/D)
5' 9.264,796 9.264,789 0,007 1: 1300.000
10' 18.529,631 18.529,579 0,052 1:360.000
15' 27.794,540 27.794,370 0,170 1:160000
O campo topográfico foi limitado a uma região definida por um círculo de raio
igual a 30Km, dentro desse campo de atuação a curvatura da terra tem influência
desprezível para efeito de levantamentos topográficos.
Ex1) Para D = 30 Km
D = D³/3R² = 30³/3(6370)²
D = 0,0002218 Km = 22,18cm
D/D = D²/3R²
D/D = 30²/3(6370)² : 30²/30²
D/D = 1/135256
D/D = 0,0000073 Km/Km
D/D = 7,3 mm/Km (erro relativo)

15. 15
1.9– EVOLUÇÃO DOS SISTEMAS GEODÉSICOS
O Sistema Geodésico Brasileiro (SGB) é composto por redes de altimetria,
gravimetria e planimetria. O Referencial de Altimetria vincula-se ao GEOIDE. O
referencial de Gravimetria está vinculado a milhares de estações distribuídas
sobre o território nacional, que recolhem dados acerca da aceleração da
gravidade. Finalmente, a definição da superfície, origem e orientação do sistema
de coordenadas usado para mapeamento e georreferenciamento no território
brasileiro é dada pelo Referencial de Planimetria, representado ainda hoje pelo
SAD-69, mas em processo de alteração.
1.9.1 SAD-69
Como já foi salientado, no Brasil, atualmente, é utilizado o Sistema
Geodésico Brasileiro. Esse sistema faz parte do Sistema Geodésico Sul-
Americano de 1969, conhecido como SAD-69, que apresenta dois parâmetros
principais: a figura geométrica representativa da Terra (o elipsoide de referência) e
sua orientação (a localização espacial do ponto de origem – base – do sistema):
a) Figura da Terra
 Elipsoide Internacional de 1967, com:
 Semieixo maior = 6.378.160,00m;
 Semieixo menor = 6.356.774,72m
 α (achatamento = (a-b/a) = 1/298,25
b) Orientação
 Geocêntrica: dada pelo eixo de rotação paralelo ao eixo de rotação
da Terra e com o plano meridiano de origem paralelo ao plano
meridiano de Greenwich, conforme o Serviço Internacional da Hora
(BIH – Bureau International de L´Heure).
 Topocêntrica: no vértice de Chuá, da cadeia de triangulação do
paralelo 20º S, com as seguintes coordenadas:

16. 16
 φ (latitude) = 19º 45’41,6527” S
 λ (longitude) = 48º 06’04,0639” WGr
 N (altitude) = 0,0m
1.9.2 SIRGAS
O Sistema de Referência para as Américas (SIRGAS) encontra-se em
implantação e esta sendo utilizado concomitantemente com o SAD-69.
O Sirgas foi concebido em função da necessidade de adoção de um
sistema de referência compatível com as técnicas de posicionamento global,
dadas por sistemas dessa natureza como o GPS. Amplamente discutido no meio
cartográfico latino-americano, ele está programado para substituir o SAD-69 ate
2015. Esse sistema leva em consideração os seguintes parâmetros:
Sistema de Referência:
 International Terrestrial Reference System (ITRS) – Sistema
internacional de referência terrestre;
 Elipsoide de Referência: Geodetic Reference System 1980 (GRS-80)
– Sistema Geodésico de Referência de 1980, com:
 Raio equatorial da Terra: a = 6.378.137 m
 Semieixo menor (raio polar): b = 6.356.752,3141m
 α (achatamento) = 1/298.257222101
1.10 ESCALAS
1.10.1 Representação Gráfica - Consiste na transferência, para o desenho, das
distâncias medidas no terreno mediante a consideração de uma determinada
escala e a utilização de convenções apropriadas para a representação dos
detalhes. Em l
le
ev
va
an
nt
ta
am
me
en
nt
to
os
s t
to
op
po
og
gr
rá
áf
fi
ic
co
os
s é necessário que você saiba:
 Dar uma noção de escala;
 Distinguir escala gráfica de escala numérica;

17. 17
 Identificar mapas de grande e pequena escala;
 Referir as características dos mapas de grande escala;
 Referir as características dos mapas de pequena escala;
 Calcular uma distância real, sabendo a distância do mapa e a escala do
mapa;
 Calcular uma distância no mapa, sabendo a distância real e a escala do
mapa; e
 Calcular a escala de um mapa, sabendo a distância no mapa e a distância
real.
Assim, escala pode ser representada como uma relação de
proporcionalidade entre as distâncias lineares num desenho (mapa) e as
distâncias correspondentes na realidade. As escalas podem ser indicadas de duas
maneiras, através de uma representação gráfica ou de uma representação
numérica.
 Escala gráfica - A escala gráfica é representada por um pequeno
segmento de reta graduado, sobre o qual está estabelecida diretamente a
relação entre as distâncias no mapa, indicadas a cada trecho deste
segmento, e a distância real de um território. Observe:
De acordo com este exemplo cada segmento de 1cm é equivalente a 3 km
no terreno, 2 cm a 6 km, e assim sucessivamente. Caso a distância no
mapa, entre duas localidades seja de 3,5 cm, a distância real entre elas
será de 3,5 X 3, ou 10,5 km (dez quilômetros e meio). A escala gráfica
apresenta a vantagem de estabelecer direta e visualmente a relação de
proporção existente entre as distâncias do mapa e do território.

18. 18
 Escala numérica - A escala numérica é estabelecida através de uma
relação matemática, normalmente representada por uma razão, por
exemplo: 1: 300 000 (1 por 300 000). A primeira informação que ela fornece
é a quantidade de vezes em que o espaço representado foi reduzido. Neste
exemplo, o mapa é 300 000 vezes menor que o tamanho real da superfície
que ele representa. Na escala numérica as unidades, tanto do numerador
como do denominador, são indicadas em cm. O numerador é sempre 1 e
indica o valor de 1cm no mapa. O denominador é a unidade variável e
indica o valor em cm correspondente no território. No caso da escala
exemplificada (1: 300 000), 1cm no mapa representa 300 000 cm no
terreno, ou 3 km. Trata-se portanto da representação numérica da mesma
escala gráfica apresentada anteriormente.
Consoante o grau de redução efetuado para realizar o mapa ter-se-á mapas
de diferentes escalas. Deve-se considerar duas grandes categorias de mapas
atendendo ao grau de redução: o mapas de grande escala e os mapas de
pequena escala. Quanto maior o denominador, menor a escala, menor o
detalhamento e maior a extensão da área mapeada. Quanto menor o
denominador, maior a escala, maior o detalhamento e menor a extensão da área
mapeada.
1.10.2 Cálculo de Escala
O cálculo de escala é dado pela razão matemática entre a distância gráfica
e a distância real, como mostra a fórmula abaixo:
E = d
D

19. 19
Onde:
E = Escala;
D = Distância natural/real
d = Distância gráfica
Unidade II – PLANIMETRIA
2.1 ORIENTAÇÃO DE PLANTAS TOPOGRÁFICAS
2.1.1 – PÓLO NORTE E PÓLO SUL VERDADEIRO OU GEOGRAFICOS OU
ASTRONÔMICOS:
A Terra na sua rotação diária gira em torno de um eixo virtual. Os pólos
norte e sul verdadeiros são os pontos de encontro desse eixo com a superfície
terrestre.
2.1.1.1 – Meridianos verdadeiros ou geográficos ou astronômicos:
É a linha que une os pólos verdadeiros da Terra.
PV
 Eixo Virtual
Meridiano Verdadeiro
PV = Direção ou Norte Verdadeiro
2.1.1.2 – Direção ou norte verdadeiros ou geográficos ou astronômicos:
É a direção dada pelo meridiano verdadeiro.
2.1.2 – PÓLO NORTE E PÓLO SUL MAGNÉTICOS:

20. 20
Tendo a Terra as propriedades de um grande magneto, as extremidades da
agulha imantada da bússola são atraídas por duas forças atuando em dois pontos
diretamente opostos. Estes pontos são os pólos norte e sul magnéticos.
2.1.2.1 – Meridiano magnético:
É a linha que liga os pólos magnéticos da Terra.
2.1.2.2 – Direção ou norte magnético:
É a direção dada pelo meridiano magnético. Desloca-se em torno do pólo
norte verdadeiro, seguindo aproximadamente um círculo.
2.1.3 – DECLINAÇÃO MAGNÉTICA LOCAL ():
É o ângulo horizontal formado entre a direção norte e sul verdadeiro e a
direção norte e sul magnética.
PNM PNV PNM

PSV PSM
PSM
2.1.3.1 – Declinação magnética oriental:
É quando o meridiano magnético fica a direita do meridiano verdadeiro.
Ex1)  = + 12o 05’12” oriental (positivo)
2.1.3.2 – Declinação magnética ocidental:
É quando o meridiano magnético fica a esquerda do meridiano verdadeiro.
Ex1)  = - 2o 11’04” ocidental (negativo)

21. 21
2.2 MEDIDAS DE ÂNGULOS
Há dois processos para medir os ângulos que os alinhamentos fazem entre
si em posição horizontal:
2.2.1 – DOS ÂNGULOS INTERNOS:
2.2.1.1 - Rumo de um alinhamento:
É ângulo horizontal formado entre as direções norte e sul verdadeira ou
magnética e o alinhamento. Medido a partir do norte ou do sul na direção do
alinhamento e variando de 0
o
a 90
o
.
Figura 01:
Diz-se que os rumos das linhas:
Ex1) A-1 = N 70
o
E ou 70
o
NE
Ex2) A-2 = S 45
o
E ou 45
o
SE
Ex3) A-3 = S 30
o
W ou 30
o
SW
Ex4) A-4 = N 60
o
W ou 60
o
NW

22. 22
2.2.1.2 - Azimute de um alinhamento:
É o ângulo horizontal formado entre as direções norte/sul verdadeira ou
magnética e o alinhamento. Medido a partir do norte para a direita ou para a
esquerda na direção do alinhamento e variando de 0o a 360o.
No hemisfério sul, e, portanto no Brasil, usa-se sempre medir o azimute a
partir do norte. Como são muito raras as ocasiões em que usar-se-á outro tipo de
azimute, quando não for expressamente afirmado o contrário, azimute será
sempre à direita do norte.
Figura 02: Dos azimutes de um alimento.
2.2.1.3 – Conversão de azimute em rumo e vice-versa:
N
4o Quadrante: 1o Quadrante:
R = 360o – Az R = Az
W E
3o Quadrante: 2o Quadrante:
R = Az – 180o R = 180o – Az
S
Figura 03: Conversão entre rumo e azimute.

23. 23
2.2.1.4 – Sentido a vante e a ré na medida dos rumos e azimutes:
O sentido a vante numa linha é aquele obedece ao sentido em que se está
percorrendo o caminhamento e o sentido a ré, o contrário a este sentido; assim,
quando se está medindo uma sucessão de linhas cujas estacas estão numeradas
como 1,2,3,4,5,6, etc., o sentido a vante da linha que liga o ponto 2 ao 3 é de 2
para 3, e o sentido a ré, o de 3 para 2.
O rumo a ré de uma linha deve ser numericamente igual ao rumo a vante,
porém com as letras trocadas. Se o rumo vante 3-4 é de N 32
o
E, o ré, isto é, 4-3
será S 32
o
W, conforme mostra a Figura 4.
Os azimutes vante e ré da mesma linha guardam entre si uma diferença de
180
o
. Se o azimute vante AB é de 110
o
, o ré será 290
o
; se o vante de CD for 320
o
,
o ré será 320
o
– 180
o
= 140
o
, de acordo com a Figura 5. O ângulo NBA é o
suplemento de 110
o
, portanto 70
o
; o azimute à direita de BA é o replemento de
70
o
:
360
o
– 70
o
= 290
o
ou seja, 110
o
+ 180
o
= 290
o
2.2.1.5 – Rumos e azimutes, magnéticos e verdadeiros:
Até o momento, quando falamos em rumos ou azimutes não foi
especificado a sua referência, a partir da linha norte verdadeiro ou magnético.
Quando o rumo é medido a partir da linha norte-sul verdadeira ou geográfica, o
rumo é verdadeiro; quando é medido a partir da norte-sul magnética, o rumo é
magnético; o mesmo se dá para os azimutes.
A diferença entre os dois rumos é a declinação magnética local. É muito
importante respeitar o sentido dos ângulos: a declinação magnética é sempre
medida na ponta norte e sempre do norte verdadeiro para o magnético e os rumos
são medidos sempre da reta NS para a linha. Inverter qualquer sentido é errado.
Ver exemplo de rumos e azimutes magnéticos na Figura 04.

24. 24
Figura 04: Rumos e azimutes Verdadeiros e magnéticos
2.2.2 – DOS SUPLEMENTOS DESTES ÂNGULOS, CHAMADOS DEFLEXÕES:
2.2.2.1 – Deflexão:
É o ângulo horizontal formado pelo prolongamento do alinhamento anterior
com o alinhamento seguinte.
Figura 05: Dos ângulos externos.

25. 25
Em uma poligonal fechada a soma algébrica dos ângulos de deflexão é
igual a 360o, porém os ângulos entrantes serão negativos. O ângulo de deflexão é
o suplemento do ângulo interno ou externo para um mesmo vértice.
DI - DE = 360
o
2.2.2.2 – Ângulo de deflexão
É o suplemento do ângulo interno ou externo para um mesmo vértice.
E B
C AIC A AIC + C = 180
o
AED + DE = 180
o
AED D
E
2.3 - COORDENADAS PARCIAIS DE UM ALINHAMENTO
As coordenadas parciais de um alinhamento são as projeções desse
alinhamento sobre os eixos Norte, Sul, Leste e Oeste.
d AB
R AB
Y AB
X AB
A
E
B
C
D
N
S
W E

26. 26
Logo:
 sen RAB = XAB/dAB
XAB = dAB . sen RAB Abscissa parcial de AB
 cos RAB = YAB/dAB
YAB = dAB . cos RAB Ordenada parcial de AB
Exemplo1:
Alinhamento Azimute Deflexão Rumo Distância
Coordenadas Parciais
E W N S
A - B AzAB RAB dAB XAB YAB
B - C DBC RBC dBC XBC YBC
C - D DCD RCD dCD XCD YCD
D - E DDE RDE dDE XDE YDE
∑ XE XW YN YS
XAE =∑XE-∑XW YAE =∑YN-∑YS
Tg RAE = XEA/YEA
RAE = arctg XEA/YEA NE
REA = arctg XEA/YEA SW
dEA = √ XEA² + YEA
DC
dAB
E
D
A
dEA
B
C

27. 27
2.4 MÉTODOS DE LEVANTAMENTOS TOPOGRÁFICOS
2.4.1 – CONCEITO:
É o conjunto de operações que realizamos no campo e no escritório a fim
de obter os dados necessários à reprodução geométrica de determinada área.
2.4.2 – FASES DE UM LEVANTAMENTO TOPOGRÁFICO:
2.4.2.1 – Reconhecimento da área:
Tem a finalidade de percorrer a região a ser levantada, elegendo-se os
principais vértices da poligonal básica o levantamento, assim como escolher e
determinar o ponto de partida do levantamento.
2.4.2.2 – Poligonal básica:
Do ponto de partida escolhido, inicia-se o levantamento da poligonal,
percorrendo todo perímetro até o seu fechamento. Durante este trabalho, serão
levantados todos os elementos que caracterizam a linha divisória da propriedade,
os acidentes existentes em suas imediações, bem como os pontos característicos
que servirão de base para as poligonais internas.
Conforme a natureza do levantamento, em vez da poligonal fechada pode-
se lançar no terreno uma poligonal aberta ou uma rede de triangulação.
Quando se tratar do levantamento de uma área relativamente extensa, é
vantajoso, em vez de um só polígono, dividi-la em duas ou mais áreas parciais.

28. 28
Figura 06: Poligonal Básica
2.4.2.3 – Levantamento de detalhes:
Feito o fechamento da poligonal básica, passa-se a lançar no interior da
área poligonais abertas partindo-se do vértice escolhido no perímetro. Estas
poligonais serão lançadas no terreno, acompanhando as estradas, cursos d’água,
fazendo-se amarrações a todas as benfeitorias existentes como a outros detalhes
importantes possibilitando desta forma definir a planimetria e altimetria do terreno
levantado
2.4.3 – TIPOS DE LEVANTAMENTOS TOPOGRÁFICOS
2.4.3.1 – Método de irradiação ou das coordenadas polares
Neste processo os pontos topográficos são definidos pelas medições de
ângulos e distâncias. O ponto topográfico P será definido medindo-se o ângulo a e
a distância D.

29. 29
Figura 07: Coordenadas Polares Figura 08: Irradiação
Este processo é empregado para levantamento de áreas pequenas e
descampadas, de maneira que de um ponto escolhido no interior delas possamos
visar todos os pontos que compõem o perímetro e também os pontos
característicos.
O processo de irradiação, somente em casos especiais de levantamento
topográfico, constitui por si só um método de levantamento, e de deve ser mais
empregado como um processo auxiliar do caminhamento.
2.4.3.2 – Levantamento da interseções ou das coordenadas bipolares
Neste método os pontos topográficos a serem levantados serão definidos
pela intercessão dos lados de ângulos horizontais medidos das extremidades de
uma base estabelecida no terreno.
Figura 09: Coordenadas Bipolares

30. 30
Neste método, a base é a única linha a medir, usando-se para isso de
preferência uma trena, fazendo-se a medição na horizontal; todas as demais
medições são angulares.
No processo de levantamento por interseções, para melhor determinar os
pontos topográficos, devemos evitar as medições de ângulos muito agudos ou
muito obtusos.
A determinação dos pontos topográficos em desenho será obtida pela
interseção dos lados de ângulos medidos no terreno formando-se uma rede de
triângulos, dos quais se conhece dois ângulos e um lado (base), de modo que os
lados poderão ser determinados por processo gráfico ou por resolução
trigonométrica.
2.4.3.3 – Levantamento por ordenadas:
Neste processo a posição do ponto topográfico é definida pela medição de
suas respectivas coordenadas retangulares. Assim, o ponto P do exemplo a seguir
será determinado medindo-se no campo a abscissa AB=x e a ordenada BP=y. As
respectivas coordenadas definidoras dos pontos topográficos são geralmente
determinadas no terreno pelo processo das medições diretas dos alinhamentos.
Figura 10: Levantamento de ordenadas.
2.4.3.4 – Levantamento por caminhamento:
Consiste em se percorrer uma série de alinhamentos, cujos comprimentos
são medidos, ligados por ângulos que também são determinados.
O caminhamento poderá ser realizado medindo-se uma linha poligonal
aberta ou uma poligonal fechada. Ao proceder-se o levantamento de um poligonal,
pode-se medir, conforme a natureza dos instrumentos, os azimutes, os rumos,

31. 31
ângulos de deflexões e ângulos internos ou externos da poligonal. Os
alinhamentos poderão ser determinados por processos de medição direta ou
medição indireta das distâncias.
O método de levantamento por caminhamento é caracterizado pela
natureza do ângulo que se mede, daí classificar-se em dois pontos.
2.4.3.4.1 – CAMINHAMENTO A BÚSSOLA:
Consiste em caminhar por todo o contorno da área do terreno a ser
levantada, medindo-se os azimutes ou rumos, conforme o limbo da bússola,
também sendo medidas as distancias de cada alinhamento.
Figura 11: Caminhamento a bússola.
2.4.3.4.2 – CAMINHAMENTO PELOS ÂNGULOS DEFLEXÕES
Figura 12: Pelos ângulos de deflexão

32. 32
2.4.3.4.3 – CAMINHAMENTO PELOS ÂNGULOS INTERNOS –
Para medição de ângulos internos, quando se trabalha com instrumentos
cuja graduação do limbo horizontal é no sentido dextrôgiro de 0o a 360o, devemos
orientar o caminhamento da poligonal básica no sentido contrário à graduação do
limbo, a fim de se ter a leitura direta dos ângulos.
Figura 13: Pelos ângulos internos
2.4.3.4.4 – CAMINHAMENTO PELOS ÂNGULOS EXTERNOS
O procedimento para este processo de levantamento é semelhante ao
anterior, mudando-se apenas o sentido do caminhamento, pois, para os aparelhos
que trazem o limbo horizontal graduado de 0o a 360o no sentido em que caminha
os ponteiros de um relógio, devemos percorrer o perímetro da poligonal
topográfica no sentido direto, idêntico ao da graduação do limbo, afim de que os
ângulos medidos pelo instrumento sejam externos.

33. 33
Figura 14: Pelos ângulos de deflexão.
2.5 CÁLCULO ANALÍTICO DE ÁREAS
Há diversos processos empregados na avaliação de áreas dos polígonos
topográficos, sendo eles:
 Geométrico – consiste em dividir o polígono em figuras geométricas
conhecidas. As medidas lineares conhecidas graficamente não são
precisas.
 Mecânico – é realizado através de um instrumento denominado planímetro
e utilizado para medir áreas de figuras geométricas irregulares.
 Analítico ou Determinantes de Gauss – é o mais usado para medição de
áreas em função da precisão obtida; consiste em determinar a área de um
polígono topográfico através das coordenadas plano-retangulares de seus
vértices.
2.5.1 – CÁLCULO ANALÍTICO OU DETERMINANTE DE GAUSS:
Seja o triângulo ABC, expresso na Figura 01, referido a dois eixos
retangulares (cartesianos) x e y. A sua área pode ser expressa em função da área

34. 34
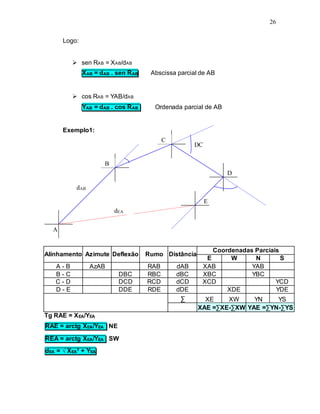
de três trapézios. Considerando os trapézios DBCF, DBAE e EACF, a área do
triângulo ABC pode da seguinte forma ser estimada:
Figura 15: Determinante de Gauss.
S (ABC) = [(DB + FC)/2 x DF] – [(FC + EA)/2 x EF] – [(EA + DB)/2 x DE
Os elementos que figuram na expressão anterior correspondem as
ordenadas e abscissas dos vértices A, B e C.
Substituindo, tem-se:
S (ABC) = [(x + x1)/2 . (y – y1)] –[(x1 +x2)/2 . (y1 – y2)] – [(x2 + x)/2 . (y2 – y)]
S (ABC) = ½ [ (x + x1) (y – y1) + (x1 +x2) (y1 – y2) + (x2 + x) (y2 – y)
2S (ABC) = [(x1y2 + x2y + xy1) – (y1x2 + y2x + yx1)]
2.5.2 – CÁLCULO DE ÁREAS EXTRAPOLIGONAIS:
2.5.2.1 – Fórmula dos trapézios ou de Bezout:
Supondo-se uma sucessão de trapézios, todos com a mesma altura d,
conforme a Figura 02, a área calculada pela fórmula de Bezout (SB) será:

35. 35
Figura 16: Método de Bezout
SB = [(y1 + y2)/2 . d] + [(y2 + y3)/2 . d] + [(y3 + y4)/2 . d] + ... + [(y6 + y7)/2 . d] + [(y7 +
y8)/2 . d]
Pondo em evidência d/2
SB = d/2 (y1+ 2y2 + 2y3 + ... + 2y7 + y8)
Resumindo:
SB = d/2 (E + 2M)
Onde:
E = y dos extremos;
M = y dos meios.
2.5.2.2 – Fórmula de Simpson:
Seja um número par de trapézios de mesma altura d (Figura 03 e 04). A
área calculada pela fórmula de Simpson (Ss) será:
Figura 17: Método de Simpson. Figura 18: Colocando 3 e 5 em
evidência

36. 36
a 1 - 3 = (y1+y3)/2 . 2d + 2/3. 2d(y2-(y1+y3)/2),
Pondo d/3 em evidência,
a 1 - 3 = d/3(3y1+3y3) + d/3(4y2-2y1-2y3),
a 1 - 3 = d/3(4y2+y1+y3)
Analogamente, a área entre 3 e 5 será:
a 3 - 5 = d/3(4y4+y3+y5)
e a área entre 5 e 7 será
a 5 - 7 = d/3(4y6+y5+y7)
Calculando então a área pela fórmula de Simpson (Ss), temos:
Ss = a 1 - 3 + a 3 - 5 + a 5 - 7
Ss = d/3 (4y2+4y4+4y6 +y1+y7+2y3+2y5)
Chamando-se de:
E = somatória dos ys extremos
I = somatória dos ys ímpares e
P = somatória dos ys pares
temos:
Ss = d/3 (E + 2I + 4P)
2.5.2.3 – Fórmula de Poncelet:
Seja um número par de trapézios de mesma altura d, ver Figura 05:

37. 37
Figura 19: Método de Poncelet.
A partir de duas áreas:
a1 – área formada por ABCDE com a linha da poligonal 1-7;
a2 – área dos trapézios formados pelas tangentes aos pontos B, C e D
também com a linha da poligonal 1-7.
Considerando que a área a ser calculada seja:
Sp = 1/2(a1+a2),
Onde:
a1 = 1/2(y1+y2)d+(y2+y4)d+(y4+y6)d+ 1/2(y6+y7)d,
a2 = 2dy2+2dy4+2dy6
Sp = 1/2(a1+a2)= d/2 (y1/2+ y2/2+ y2 +2 y4+ y6+y6/2+ y7/2+2y2 +2 y4+
2y6),
Sp = d/2(y1/2+ y7/2+ y2/2+ 3y2+3y4 +3 y6+ y6/2),
Somando-se e subtraindo-se y2/2 e y6/2, temos:
Sp = d/2(y1/2+ y7/2+ 4y2+4y4+4y6 –y2/2- y6/2),
Sp = d/2(4P + (E – E’)/2),
Chamando-se de:
P = somatória dos ys pares
E = somatória dos ys extremos
E’= somatória dos ys adjacentes aos extremos, ou seja segundo e
penúltimo y.
temos:

38. 38
Sp = d(2P + (E – E’)/4)
Unidade III – ALTIMETRIA
3.1- GENERALIDADES:
 A altimetria tem por finalidade a medição da distância vertical ou diferença
de níveis entre diversos pontos.
 Recorre-se ao nivelamento sempre que for necessário determinar as
distâncias verticais relativas de uma série de pontos.
 As distâncias verticais existentes entre os planos horizontais que passam
em cada um dos pontos considerados, são denominadas de diferença de
nível.
 O plano horizontal de referência para os trabalhos de nivelamento é o do
nível do mar, isto é, o plano horizontal local que guarda a mesma distância
do nível do mar ao centro da Terra.
 O nível do mar fica então sendo o plano de referência para todos os
trabalhos de altimetria, seja qual for o local da Terra em que nos
encontramos.
 Sempre que necessitarmos de nivelamentos que serão utilizados em
projetos de importância, eles devem se referir ao nível do mar, porém,
quando efetuarmos levantamento de interesse apenas particular podemos
fixar uma referência de nível arbitrária escolhendo-se, nesse caso, um valor
inteiro qualquer, estipulando que um determinado ponto possui, por
exemplo, cota ou elevação de 100m.
 Quando o plano de referência é arbitrário, ou seja, um plano horizontal ou
de nível situado acima ou abaixo do nível médio do mar, o nome dado à
distância vertical, relativa a este plano, será denominada cota ou elevação.
 A distância vertical quando o plano de referência é o nível médio do mar,
recebe o nome de altura ou altitude.

39. 39
 DATUM será, portanto, o nome dado ao plano de referência em qualquer
dos dois casos anteriores.
Cota ou elevação
Plano de referência Altura ou Altitude Cota
Zero (DATUM)
Plano arbitrado Cota Zero
(DATUM)
Figura 20: Plano de referência .
3.2 – ERRO ALTIMÉTRICO
Figura 21: Erro altimétrico
Seja:

40. 40
Pp = cota de P sobre a esfera terrestre
Pp’ = cota de P sobre a tangente T
p’p = h (erro de esfericidade absoluto)
r = p’r = 0,15 h
h’ = rp (erro resultante)
h’ = h - r
3.2.1 – Erro de esfericidade absoluto:
môp = p’o² = om² + mp’²
(R + Dh)² = R² + D’²
R² + 2Rh + h² = R² + D’²
h (2R + h) = D’²
h .2R = D’²
h = D’2/2R
h = (Km² x D’²)/2 x 6370Km
h = (1xKmxD’²)/12740
h = 0,000078KmD’²
h(m) = 0,08D’² Km
r = 0,15 x h
r = 0,15 x 0,08D’2
r = 0,012D’2
r(m) = 0,01D’2
h’ = h - r
h’ = 0,08D’² – 0,01D’²
h’ = 0,07D’²

41. 41
3.3– TOLERÂNCIA ALTIMÉTRICA
Nos nivelamentos é relativamente fácil conseguir bons resultados, devido
aos métodos e à elevada precisão dos aparelhos.
Entretanto, o erro tolerável em nivelamento geométrico, pode ser fixado no
seguinte intervalo:
E = ± e  D até EM = ± m.e  D
E = erro médio provável em cm;
EM = erro máximo tolerável;
e = coeficiente de precisão conseguida pelo instrumento;
m = coeficiente de precisão, variável com o critério adotado para o trabalho em
vista; e
D = extensão percorrida em Km.
 Erros permitidos em nivelamento:
3.4– AJUSTAMENTO ALTIMÉTRICO:
3.4.1 – Para polígonos fechados:
Ecm = Ec/ l
3.4.2 – Para polígonos abertos:
Ecm = Ec/ 2 x l
1,2  D’
0,1
100
Precisão
2,4  D’
0,5
150
Precisão ordinária
9,5  D’
5
300
Pouca precisão
Erro Tolerável
(cm)
Precisão na leitura da
mira (cm)
Distância
Máxima de
visada (m)
Classe de
nivelamento

42. 42
Onde:
Ecm = erro de cota por metro;
Ec = erro total de cota; e
l = distância horizontal percorrida desde zero até o ponto n, em metros.
3.5 - MÉTODOS GERAIS DE NIVELAMENTO
Os nivelamentos são classificados de acordo com a ordem de precisão dos
resultados, sendo eles, em ordem decrescente de precisão:
3.5.1 - Nivelamento geométrico ou direto ou por gravidade ou por alturas –
podendo ser simples ou composto.
3.5.2 – Nivelamento trigonométrico ou indireto ou por declive – baseado na
resolução de um triângulo retângulo construído no plano vertical.
3.5.3 – Nivelamento barométrico ou físico – tem por base as diferenças de
pressões atmosféricas em diferes altitudes.
3.6 NIVELAMENTO GEOMÉTRICO
3.6.1 – NIVELAMENTO GEOMÉTRICO SIMPLES:
É aquele que com uma só estação do aparelho pode-se determinar a cota
de todos os pontos de terreno a serem nivelados.
3.6.1.1 – Diferença de nível entre dois pontos:
Consiste em se fazer passar uma reta horizontal sobre os dois pontos
medindo-se as distâncias verticais l1 e l2 entre a reta e os pontos A e B. O valor l2
- l1 representa a diferença de elevação entre os dois pontos.

43. 43
Figura 22: Diferença de nível entre dois pontos.
3.6.1.2 – Diferença de nível entre vários pontos:
Para estudarmos as diferenças de nível relativas entre uma série de pontos
é necessário que se conheça a distância vertical entre um deles e o plano de
referência. Convenciona-se chamar esse ponto, de referência de nível (RN).
A parte prática da operação consiste em estacionar o nível de tripé em um
ponto qualquer de onde se possa observar a mira, colocada sucessivamente em
cada um dos pontos, efetuando leituras na interseção do fio médio (fio nivelador).
Por outro, para se determinar à cota do ponto onde está a mira,
independente de sua direção, faz-se uma visada a vante.
Figura 23: Diferença de nível entre vários pontos.

44. 44
Instalado o nível de luneta em M, não precisa situar-se na linha a nivelar e
sim, aproximadamente equidistante dos pontos extremos.
A altura do instrumento (AI), em nivelamento, é a altura do eixo óptico
acima do plano de referência ou DATUM. Para determina-la faz-se uma leitura
inicial num ponto de cota conhecida ou arbitrária.
Seja A esse ponto, de cota (CA) e (Vra) a leitura de visada de ré.
Assim, a cota do plano horizontal de referência para o cálculo de todas as
outras cotas será:
AI = CA + Vra
A cota do ponto extremo D (CD), equidistante de A, é obtida em função da
visada vante feita em D (VD) e assim:
CD = AI - Vd
 Duas, portanto, são as regras para nivelar:
1. A altura do instrumento (AI) é igual à soma da visada ré (Vré) com a cota do
ponto onde a mesma foi feita; e
2. A cota de um ponto, em função da altura do instrumento (AI), é a diferença
entre tal altura e a visada de vante (Vv) lida no mesmo ponto.
3.6.2 – NIVELAMENTO GEOMÉTRICO COMPOSTO:
Quando o desnível é superior a altura da mira, isto é, a 4m, o nivelamento
será composto, exigindo mais de uma estação do nível. Decompõe-se o trecho a
nivelar em outros que possam ser nivelados convenientemente.
Instalado o nível num ponto M, por exemplo, é feita uma visada a ré,
máxima no ponto A, início da poligonal a nivelar, e outra a vante, mínima, no ponto

45. 45
B e assim, sucessivamente, até atingir o alto da rampa. Na contra-rampa, as
visadas são contrárias, isto é, mínimas a ré e máximas a vante.
No nivelamento geométrico composto, tem-se as visadas a vante de
mudança e intermediária que servem para determinar a cota do ponto onde está a
mira. Entretanto, na primeira este ponto vem a receber posteriormente uma visada
à ré, e no outro caso tal não acontece.
Figura 24: Nivelamento Composto
A diferença de nível entre os pontos A e B, será:
n1 = CB – CA = r1 – v1
Entre os pontos B e C
n2 = CC – CB = r2 – v2
A diferença de nível entre os pontos extremos, será:
N = CE – CA = (r1+ r2+ r3+ ...+ rn ) – (v1+ v2+v3+...+ vn)
N = r -  v
O nivelamento geométrico composto pode ser de poligonal aberta ou
fechada
a) Nivelamento Geométrico Composto de uma Poligonal Aberta – É o caso
mais comum de nivelamento. É necessário conferir o nivelamento, através
do contra-nivelamento. Contra-nivelamento é uma segunda operação de

46. 46
nivelamento entre referências de nível situadas nos extremos das seções
niveladas, correspondendo à operação de volta.
b) Nivelamento Geométrico Composto de uma Poligonal Fechada - Quando o
ponto inicial é o mesmo ponto de chegada do nivelamento. A diferença
entre as altitudes/cotas de saída e chegada é o erro cometido no
nivelamento.
De acordo com o instrumento empregado e a natureza dos trabalhos que se
realizam, os nivelamentos geométricos podem ser classificados em:
Classificação Tipo de Nivelamento e (mm/km)
A Alta precisão 1,5 a 2,5
B Precisão
B1 Precisão de 1a Ordem 5
B2 Precisão de 2a Ordem 10
B3 Precisão de 3a Ordem 15
B4 Precisão de 4a Ordem 20
B5 Precisão de 5a Ordem 25
 Erro Cometido (Ec) ==> Ec = Altitude final (cota) – Altitude inicial
(cota)
 Distribuição do erro: Usualmente, a distribuição do erro poderá ser
feita em partes iguais pelo número de alturas de instrumento.
N = Ec
n. AI

47. 47
3.7 – NIVELAMENTO TRIGONOMÉTRICO
O Perfil longitudinal é a maneira de realizar a representação gráfica de um
levantamento altimétrico, como se pode observar na figura abaixo
Figura 25: Perfil longitudinal
O Perfil é a representação gráfica do nivelamento e a sua determinação tem
por finalidade:
1. O estudo do relevo ou do seu modelado, através das curvas de nível;
2. A locação de rampas de determinada declividade para projetos de
engenharia e arquitetura;;
3. O estudo dos serviços de terraplanagem (volumes de corte e aterro).

48. 48
3.7.1 - CÁLCULO DO GREIDE EM UM PERFIL DE NIVELAMENTO
O Greide é a linha que acompanha o perfil, dotada de uma certa
declividade, e que mostra o quanto o solo deve ser cortado ou aterrado. A Cota
vermelha (CV) é a distância vertical entre um ponto qualquer do greide e um
ponto correspondente no terreno. Pode ser positiva (aterro) ou negativa (corte) e o
Ponto de passagem é o ponto onde o greide coincide com o ponto do terreno,
não havendo corte ou aterro (ponto C).
Figura 26: Perfil do greide.
Em Perfis longitudinais no eixo das ordenadas (y) são apresentadas as
cotas altimétricas e, no eixo das abscissas (x) são representadas as estacas ou
distâncias horizontais correspondentes (no caminhamento do eixo da rodovia). (A
escala do eixo das ordenadas é, quase sempre, dez vezes maior que a das
abscissas).

49. 49
O nivelamento trigonométrico é empregado quando se trata de determinar a
diferença de nível entre dois pontos acessíveis, separados por grande distância,
ou quando se tem um ponto acessível e outros inacessíveis. Nestes casos, aplica-
se o processo de interseção conjugado com resoluções trigonométricas. Para
medir as distâncias verticais, conta-se com o auxílio da mira e os ângulos de
inclinação do terreno são medidos com o emprego do teodolito.
3.7.2. DETERMINAÇÃO DA DIFERENÇA DE NÍVEL
O nivelamento trigonométrico baseia-se no valor da tangente do ângulo de
inclinação do terreno, pois o valor desta função trigonométrica representa sempre
a diferença de nível por metro de distância horizontal medida no terreno, entre os
pontos considerados.
Assim, determinando a distância horizontal (DH) entre os pontos em estudo
e o ângulo de inclinação do terreno entre eles (á), a diferença de nível (DN) é
calculada aplicando-se a seguinte fórmula:
Figura 27: Diferença de nível
DN = DH.tg α,
tg α = BB’ / AB’ t
g α = DN / DH
DN = DH.tg α

50. 50
3.8 – CURVAS DE NÍVEL
3.8.1 – DEFINIÇÃO:
É a linha determinada pela interseção do terreno com um plano horizontal,
que une pontos de igual cota. Portanto, as curvas de nível, são dadas pela
projeção sobre o plano de referência das interseções de superfície física
considerada, com planos paralelos ou de referência, ver Figura 28:
Figura 28: Formas de representação das curvas de nível.

51. 51
3.8.2 – CARACTERÍSTICAS PRINCIPAIS DAS CURVAS DE NÍVEL:
 São curvas de cotas inteiras, como mostra a Figura 01;
 São curvas regulares ou irregulares, abertas ou fechadas, concêntricas ou
não;
 Para que seja mais objetiva a representação do relevo do terreno, o
espaçamento das curvas deve ser constante. Dependendo do objetivo do
trabalho, pode-se espaçar as curvas a cada meio metro, ou a cada 1 ou
2,... 10,..., 20 metros, ver Figura 28;
 Uma curva de nível está sempre entre uma correspondente a maior
elevação e uma correspondente a menor elevação;
 Curvas de nível fechadas indicam uma elevação ou uma depressão do
terreno. Ver Figuras 29,30, 31 e 32;
Figura 29 e 30: Representação de elevações.

52. 52
Figura 31 e 32: Representação de Depressões.
 Quando um plano tangencia o terreno, o que é raro, a curva de nível se
transformará num ponto;
 A distância horizontal entre as curvas de nível é inversamente proporcional
ao aclive ou declive do terreno. Assim, quanto mais inclinado seja o terreno,
mais próximas estarão as curvas de nível, ver Figura 33;
Figura 33: Relação com a distância horizontal das curvas.
 Quando o declive ou aclive é uniforme as curvas de nível serão
equidistantes, ver Figura 34:

53. 53
Figura 34: As curvas são equidistantes.
 Linha ou reta de maior declive é a menor distância entre duas curvas de
nível consecutivas, portanto, ela é normal às curvas de nível, como mostra
a Figura 35;
Figura 35: Retas de maior declive, menor distâncias entre curvas
 Em superfícies planas e inclinadas (taludes), as curvas de nível são retas e
paralelas entre si, ver Figura 36;

54. 54
Figura 36: Taludes
 Duas curvas de nível jamais se cruzam, porque disto resultaria um único
ponto com duas elevações diferentes. Salvo em caso de uma concavidade
na encosta de uma elevação, de acordo com as Figuras 37 e 38;
Figura 37: Curvas não se cruzam Figura 38: Concavidade entre as curvas.
 Uma curva de nível não pode desaparecer repentinamente, ver Figura 39;
Figura 39: Curvas não desaparecem

55. 55
3.8.3 – INTERPRETAÇÃO DAS CURVAS DE NÍVEL:
A superfície topográfica (terrestre) por mais complexa que seja, pode ser
considerada como um conjunto de elementos (acidentes) pouco numerosos, assim
tem-se:
3.8.3.1 – Vertente ou encosta ou flanco:
É toda superfície compreendida entre a linha do vértice e a linha da base do
terreno em declive. Ver Figuras 40 e 41:
Figura 40 e 41: Modelos de Vertente
 Os tipos básicos de vertente são: Plana ou Uniforme, Côncava e Convexa.
3.8.3.1.1 – VERTENTE PLANA OU UNIFORME: é aquela que apresenta
declividade constante e curvas de nível igualmente espaçadas.
Figura 42 e 43: Vertentes planas

56. 56
3.8.3.1.2 – VERTENTE CÔNCAVA: as cotas diminuem à medida que a encosta
se aproxima do talweg, isto é, a encosta desce; como também, as curvas de
nível se aproximam do talweg.
Figura 44 e 45: Vertente Côncava
3.8.3.1.3 – VERTENTE CONVEXA: as cotas aumentam à medida que a encosta
se aproxima da cumeada, isto é, a encosta sobe; como também, as curvas de
nível se aproximam da cumeada.
Figura 46 e 47: Vertente Convexa
 Duas vertentes podem se ligar, de três maneiras: Pela parte superior, pela
parte inferior e lateralmente.

57. 57
3.8.3.1.4 – LINHA DE CRISTA OU CUMEADA OU FÊSTO OU DIVISOR DE
ÁGUAS: é quando as vertentes se ligam pela parte superior, ver Figuras: 42 e 43.
3.8.3.1.5 – TALWEG OU REUNIÃO DE ÁGUAS OU ÁLVEO: é quando as
vertentes se ligam pela parte inferior, ver Figuras 44 e 45.
3.8.3.1.6 – LATERALMENTE: duas vertentes se ligam, ora em ângulo diedro
convexo, ora em ângulo diedro côncavo.
 LIGAÇÕES EM ÂNGULO DIEDRO CONVEXO: estas ligações apresentam
três formas de combinações dos elementos comuns das vertentes
originárias: Espigão, Garupa e Esporão.
a) ESPIGÃO: é quando as vertentes têm inclinações rápidas e uniformes,
provocando na sua representação curvas de nível cuneiformes (forma de
cunha) graças a um 6angulo diedro pequeno por eles for formado. A linha de
interseção dos dois flancos é chamada Dorso, ver Figura 48:
Figura 48: Modelo de espigão.
b) GARUPA: é quando as vertentes são mais ou menos recortadas ou
dobradas, ligando-se por uma crista abaulada e quando as curvas de nível
acusam o mesmo arredondamento.

58. 58
Figura 49: Garupa.
c) ESPORÃO: é quando a linha de crista resultante da união das
vertentes se apresenta com uma inflexão acusando uma elevação ou cume
mais ou menos pronunciado.
Figura 50: Esporão
 LIGAÇÕES EM ÂNGULO DIEDRO CÔNCAVO: esta ligação representa só
uma forma de combinação dos elementos comuns das vertentes
originárias: Ravina ou Grota.
a) RAVINA OU GROTA: é quando as vertentes se ligam lateralmente, mas em
ângulo diedro côncavo e provocam uma linha de reunião de águas, como um
verdadeiro sulco mais ou menos profundo na encosta de uma elevação.
Nestes casos, as cotas de menor valor envolvem as de maior valor.

59. 59
Figura 51: Ravina ou grota
3.8.4 – FORMAS GERAIS DO MODELADO TOPOGRÁFICO:
Examinando em conjunto as formas que constituem o modelado atual da
superfície da Terra, classificar-se-á estas formas em Elevação e Depressão.
3.8.4.1 – Elevação:
É a forma exterior da superfície da Terra que apresenta relevo elevado.
Graficamente, as curvas de nível apresentam-se encaixadas umas nas outras,
com as curvas de cota de menor valor envolvendo as de maior valor, de acordo
com a Figura 52.
Figura 52: Elevação

60. 60
3.8.4.2 – Depressão:
É a forma exterior da superfície da Terra que apresenta relevo em
depressão. Graficamente, as curvas de nível apresentam-se encaixadas umas nas
outras, com as curvas de cotas maiores envolvendo as de cotas menores, como
mostra a Figura 53.
Figura 53: Depressão
3.8.5 – FORMAS DE ACIDENTES DO TERRENO:
As formas que constituem os acidentes do terreno se classificam em formas
simples ou elementares e formas compostas ou derivadas.
3.8.5.1 – Formas simples ou elementares:
Duas são as formas simples dos acidentes topográficos: Tergo ou Vale, das
quais se derivam todas as outras formas existentes na superfície da Terra.
3.8.5.1.1 – TERGO: é o acidente topográfico formado pelo encontro de duas
vertentes e um divisor de águas. Graficamente, as curvas de nível de cotas de
menor valor envolvem as de maior valor, ver Figura 54:

61. 61
Figura 54: Cumeada
3.8.5.1.2 – VALE: é o acidente topográfico formado pelo encontro de dois flancos
(vertentes) e um talweg. Graficamente, as curvas de nível de cotas de maior
valor envolvem as cotas de menor valor, ver Figura 55.
Figura 55: Talweg
3.8.5.2 – Formas compostas ou derivadas:
São os resultados das combinações entre as formas simples. O terreno
entre dois tergos, conforme sua extensão longitudinal e transversal, é chamado
Desfiladeiro, Corredor e Garganta.
3.8.5.2.1 – DESFILADEIRO: é uma passagem mais ou menos longa, cujas
vertentes apresentam fortes elevações e de acesso bastante difícil, ver Figura 56.

62. 62
Figura 56: Desfiladeiro
3.8.5.2.2 – CORREDOR: é caracterizado por uma passagem de extensão
apreciável sendo que as elevações que o formam podem ou não ser acessíveis,
como mostra a Figura 57:
Figura 57: Corredor
3.8.5.2.3 – GARGANTA: é uma passagem curta e estreita que põe em
comunicação duas vertentes, ver a Figura 31. Garganta é também chamado ao
ponto comum de uma linha de cumeada com um talweg. A garganta é também
chamada de Colo ou Quebrada. Na prática, geralmente chama-se garganta a
passagem curta e estreita já vista e Colo ou Quebrada ao ponto mais baixo da
garganta.

63. 63
Figura 58: Garganta
Figura 59: Modelados topográficos
3.8.6 – CLASSIFICAÇÃO DO RELEVO:
Segundo o aspecto que o terreno apresenta, o relevo pode ser:
3.8.6.1 – Plano:
Diferença de nível quase nula.

64. 64
3.8.6.2 – Ondulado:
Quando o terreno oferece pequenos desníveis, inferiores a 20m.
3.8.6.3 – Movimentado:
Quando o terreno apresenta uma série de elevações e depressões muito
aproximadas. Elevações entre 20 a 50m.
3.8.6.4 – Acidentado:
Quando o terreno apresenta desníveis muito sensíveis e aproximados.
Elevações entre 50 e 100m.
3.8.6.5 – Montuoso:
Elevação entre 100 e 1000m.
3.8.6.6 – Montanhoso:
Quando o terreno é ocupado por um conjunto de elevações de uma cadeia
de montanhas. Elevações superiores a 1000m.
* Outras formas compostas dos principais acidentes topográficos cuja
representação cartográfica interessa à Topografia podem ser resumidas em:
1. ELEVAÇÕES:
 Cordilheira: grandes cadeias de montanhas de elevadas altitudes
de onde partem os contrafortes secundários e, destes, os espigões;
 Serra: cadeia de montanhas de forma muito alongada, cuja parte
mais elevada apresenta-se como dentes de serra;
 Montanha: termo genérico que exprime um aglomerado de
elevações de formas e naturezas diferentes, unidas entre si em uma
extensão considerável, em que o comprimento sempre excede a
largura; alturas superiores a 400m;

65. 65
 Cimo ou Cabaço: é a parte mais elevada de uma montanha.
Quando é mais arredondada chama-se Pico; quando é pontiaguda
recebe o nome de Agulha;
 Colina: menos elevada que a montanha, de forma alongada, com
declive menos pronunciado, e em geral, coberto de vegetação. A
altura varia entre 200 a 400 metros;
 Monte: elevação de forma variável, as vezes abrupta, com pouca
vegetação na parte superior. A altura varia entre 200 a 300 metros.
 Morro: Elevação semelhante ao monte, mas de menor altura (entre
100 a 200 metros);
 Mamelão: de forma arredondada, mais ou menos cônica nos flancos
e aproximadamente esférica no vértice. É a forma mais regular entre
todas as elevações (100 a 200 metros); são muito comuns ao sul de
Minas Gerais, em virtude de serem os terrenos mais antigos do
mundo, na opinião do sábio Dr. Lund;
 Outeiro: elevação isolada em forma de colina, nas planícies ou
planaltos;
 Cerro ou montículo: elevação penhascosa ou coberta de
vegetação, com cerca de 100m;
 Chapelão: elevação extensa e achatada, de contorno arredondado,
algumas angulosas por um lado e outras alongadas em ramificações;
 Coxilha: elevação de terreno, bastante alongada, de suaves
declives e de alturas variáveis de 50 a 100m. Comuns na campanha
e no planalto do Rio Grande do Sul. Correspondem
aproximadamente aos tabuleiros dos estados do nordeste e às
lombas do Mato Grosso;
 Dobra: elevação alongada como a coxilha, mas cuja altura não vai
ordinariamente além de 20m ( Rio Grande do Sul).

66. 66
2. DEPRESSÕES:
 Garganta: é a parte mais baixa de um divisor de águas e por onde
passam as rodovias e as estradas de ferro, que ligam as planícies
aos planaltos;
 Brecha: é uma garganta bastante estreita e profunda.
 Cañon: garganta estreita e profundíssima, produzida pelo trabalho
da erosão das águas correntes. Exemplo muito conhecido é o
famoso Cañon do Rio Colorado, nos Estados Unidos, com mais de
1000m de profundidade;
 Planalto: vasta extensão de terreno, mais ou menos plana, situada
no interior dos continentes, às vezes a mais de 1000m acima do
nível do mar, como os Campos Gerais, no estado do Paraná;
 Planície: vasta extensão de terreno, bastante plana, próximo ao mar;
 Vale: grande depressão de terreno, situado entre morros ou
montanhas;
 Valado: depressão circular, vasta e profunda;
 Cuba: depressão circular, pouco extensa.
UNIDADE IV - FOTOGRAMETRIA
4.1 – DEFINIÇÃO:
A fotogrametria pode ser definida como segue:
 Medições gráficas por meio da luz. É uma definição etimológica e deriva de
três raízes gregas:
Photós: luz;
Gramma: gravar, escrever;
Metria: medição ou medida.

67. 67
E considerada a ciência e arte de obter medidas dignas de confiança
utilizando-se fotografias. É uma definição científica dada pela AMERICAN
SOCIETY OF PHOTOGRAMMETRY. É a arte, ciência e tecnologia de obter
informações seguras acerca de objetos físicos e do meio, através de processos de
registros, medições e interpretações das imagens fotográficas e padrões de
energia eletromagnética registrados. Esta definição aparece na Revista
PHOTOGRAMMETRIC ENGINEERING AND REMOTE SENSING.
4.2 – APLICAÇÕES:
É difícil enumerar todas as aplicações atuais da fotogrametria, devido ao
seu grande desenvolvimento.
Tanto as fotografias por si mesmas, como os mapas obtidos a partir delas,
têm valiosas aplicações, seja na Engenharia Civil, nos setores de urbanismo,
construção de rodovias e ferrovias, na implantação de barragens, trabalhos
portuários, cadastros fiscais, etc., seja na agricultura, na extração de minérios,
geologia, etc.
As aplicações principais são: confecções de mapas topográficos, temáticos
e mosaicos. O mapa assume características especiais segundo a finalidade para a
qual é elaborado; em função destes propósitos diretos, define-se a escala da
fotografia, o tipo de câmara aérea, o número de pontos de apoio, o tipo de filme,
etc.
A vantagem da fotogrametria está na visualização tridimensional do relevo.
4.3 – CLASSIFICAÇÃO DA FOTOGRAMETRIA:
O rápido desenvolvimento tecnológico da fotogrametria e suas múltiplas
aplicações criaram a necessidade de dividi-la em grandes grupos, segundo os
diversos pontos de vista. Assim, segundo o tipo e posição espacial da câmara e a
finalidade da fotogrametria, esta pode ser classificada em cinco grandes grupos:

68. 68
4
4.
.3
3.
.1
1 –
– F
Fo
ot
to
og
gr
ra
am
me
et
tr
ri
ia
a t
te
er
rr
re
es
st
tr
re
e:
: S
Sã
ão
o u
ut
ti
il
li
iz
za
ad
da
as
s f
fo
ot
to
og
gr
ra
af
fi
ia
as
s t
ti
ir
ra
ad
da
as
s d
de
e e
es
st
ta
aç
çõ
õe
es
s
f
fi
ix
xa
as
s e
e g
ge
er
ra
al
lm
me
en
nt
te
e t
ti
ir
ra
ad
da
as
s d
de
e e
es
st
ta
aç
çõ
õe
es
s f
fi
ix
xa
as
s e
e g
ge
er
ra
al
lm
me
en
nt
te
e d
de
e p
po
os
si
iç
çõ
õe
es
s
d
de
et
te
er
rm
mi
in
na
ad
da
as
s s
so
ob
br
re
e o
o t
te
er
rr
re
en
no
o,
, c
co
om
m o
o e
ei
ix
xo
o ó
ót
ti
ic
co
o d
da
a c
câ
âm
ma
ar
ra
a n
na
a p
po
os
si
iç
çã
ão
o h
ho
or
ri
iz
zo
on
nt
ta
al
l.
.
4.3.2 – Fotogrametria aérea: São utilizadas fotografias da superfície terrestre,
tiradas do espaço com o eixo ótico da câmara na posição vertical.
4.3.3 – Fotogrametria espacial: Abrange os aspectos da fotografia extraterrestre
e as medições feitas com câmaras fixas colocadas na Terra, na lua, em satélite
artificial, ou em outros corpos localizados no espaço.
4.3.4 – Fotogrametria não-topográfica: Tem aplicação em alguns campos da
Engenharia, na balística, na atividade policial, na solução de problemas de tráfego
e outros.
4.3.5 – Fotogrametria analítica: É aquela em que as soluções de restituição e de
transformação de coordenadas fotográficas em coordenadas terrestre são obtidas
através dos métodos matemáticos.
Vale ressaltar que a fotogrametria aérea é mais utilizada e sua sugestão de
utilizar fotografias aéreas apareceu na França, através de um balão. Em 1858, a
partir de um balão nas proximidades de Paris, foram tiradas as primeiras
fotografias aéreas, nas quais podiam ser reconhecidas as casas. O maior
desenvolvimento, contudo, aconteceu durante a 1o Grande Guerra, onde a RAF
obteve fotografias aéreas do território alemão. Hoje em dia, o desenvolvimento é
tão grande que aviões supersônicos tomam fotos a mais de 20.000m de altitude.
Através da fotografia aérea é possível tirar conclusões a cerca do tipo de solo, de
rocha, da ausência ou presença de rios e mares, da topografia do local, etc.
4.4 – PROCEDIMENTO DO VÔO:

69. 69
Ao se planejar o recobrimento aéreo fotogramétrico de uma determinada
área, um avião devidamente provido com uma câmara montada no seu “chão”
deverá executar uma série de linhas de vôo dispostas de acordo com a forma da
área a ser estudada. A existência de três parafusos calantes permite o
nivelamento da câmara em pleno vôo. O funcionamento da câmara é totalmente
automático. Um motor elétrico comanda a passagem do filme e outro, o disparo do
obturador da câmara. Cada fotografia é devidamente numerada, de tal maneira
que a série numérica indique o número da obra e o número individual de cada
foto.
Ex1) Obra 209 corresponderia ao vôo fotográfico sobre o Rio Paraná.
Ex2) 33, 34, etc (o número individual da foto).
Para o levantamento de uma zona, o avião deve voar a uma altura a mais
constante possível, ao longo das linhas de vôo paralelas e equidistantes, de tal
maneira que as fotografias se superponham lateral e longitudinalmente. Este
procedimento de superpor uma fotografia à outra é chamado de recobrimento.
Entende-se, pois, por recobrimento, a presença de pontos comuns em duas
fotografias consecutivas.

70. 70
O custo dos levantamentos aerofotogramétricos varia de caso para caso.
Paralisações de vôo devido ao mau tempo podem encarecer bastante o
levantamento. A escala solicitada também influirá no custo, uma vez que, um
levantamento na escala 1: 50000 custará cerca da metade de um na escala
1:25000.
Em linhas gerais, o preço filme e do papel fotográfico equivale ao da hora
do vôo.
A escala de uma fotografia aérea pode ser determinada através de duas
fórmulas, expressas a seguir:
E = f = distância focal
h altura do avião
E = DF = distância na foto = ab
DT distância na terra AB
A distância focal das câmaras pode variar, sendo as mais comuns as de
156mm, 210mm e 300mm. A escala da fotografia é estabelecida em função do
tipo de trabalho. Nos casos de reconhecimento geológico ou construção de
estradas, usam-se as escalas de 1:45000 ou 1:25000, enquanto que para
construção de barragens ou pesquisa de materiais de construção, a escala deve
ser 1:10000 ou 1:5000. Para cadastros fiscais, a de 1:1000 é a mais indicada.
4
4.
.5
5 –
– C
CL
LA
AS
SS
SI
IF
FI
IC
CA
AÇ
ÇÃ
ÃO
O D
DA
AS
S F
FO
OT
TO
OG
GR
RA
AF
FI
IA
AS
S A
AÉ
ÉR
RE
EA
AS
S:
:
As fotografias aéreas são agrupadas em dois tipos: verticais e oblíquas, dos
quais o maior interesse recai sobre as verticais.
4
4.
.5
5.
.1
1 –
– F
Fo
ot
to
og
gr
ra
af
fi
ia
as
s a
aé
ér
re
ea
as
s o
ob
bl
lí
íq
qu
ua
as
s:
: Há a formação de um ângulo de valor
variável, entre o plano vertical e o eixo da câmara, como mostra a Figura 02
2.
.

71. 71
4
4.
.5
5.
.2
2 –
– F
Fo
ot
to
og
gr
ra
af
fi
ia
as
s a
aé
ér
re
ea
as
s v
ve
er
rt
ti
ic
ca
ai
is
s:
: E
Essas fotografias são obtidas quando o eixo
da câmara coincide com o plano vertical, ver Figura 02. A fotografia aérea vertical
tem uma aparência plana, isto é, torna difícil ao observador não experimentado
distinguir, por exemplo, as colinas dos vales. Porém essa separação e a ideia de
relevo são possibilitadas pela estereoscopia.
4
4.
.6
6 –
– E
ER
RR
RO
OS
S E
E D
DI
IS
ST
TO
OR
RÇ
ÇÕ
ÕE
ES
S:
:
As fotografias aéreas, mesmo quando obtidas em condições favoráveis,
estão sujeitas a certos pequenos que são devidos aos seguintes fatores:
 Dificuldade em se voar em linha reta, tanto vertical como horizontalmente;
 Dificuldade de se evitar a inclinação do avião e, portanto, a da câmara
durante o vôo.
 Provido de um bom mapa aeronáutico, um piloto experimentado, voando
entre 3000m a 4500m de altura, poderá manter sua trajetória a menos de
um grau da direção desejada, e as variações de altitude não serão maiores
do que 30m, quando a região for aplainada. Em alturas mais baixas,
entretanto, as condições atmosféricas são mais variáveis e os vôos, mais
instáveis.
 Um exemplo elementar de distorção nas medidas e distâncias de uma
fotografia é dado a seguir: se executarmos um vôo a uma altitude de
4000m, com máquina fotográfica de distância focal igual a 200mm, o topo

72. 72
de um morro de 100m de altura situado na fotografia a 5cm do ponto central
dessa fotografia, sofrerá um deslocamento de 1,25mm. Se a altura do
morro for de 400m ao invés de 100m, o deslocamento será da ordem de
5mm. No caso de topo hipotético, o morro se situará na fotografia a 10cm
do ponto central, Isto é, bem na beira da fotografia ele apresentará um
deslocamento de 1cm. Dessa forma, a melhor maneira de se obterem
fotografias razoáveis para confecção de mosaicos será o aproveitamento
somente da parte central da foto.
 Distorções devidas ao deslocamento ou inclinações do avião: nesse caso, a
inclinação do eixo ótico é causada pelas oscilações do avião. Essas
inclinações podem ser laterais e longitudinais, isto é, o avião inclina
respectivamente suas asas ou sua cabina. Normalmente o avião não deve
se inclinar mais do que 4o e no caso de valores maiores que esses, as
fotografias não serão utilizadas.
 Distorções devidas ao relevo: na fotografia vertical, somente seu ponto
central é projetado verticalmente num plano horizontal. Os pontos restantes
são projetados conicamente e, por esta razão, deslocados da sua
verdadeira posição. A figura 03 a seguir ilustra um perfil topográfico com
vale e colina. Pode-se notar que o ponto A é registrado com a e o ponto B
como b. Dessa maneira, o ponto a estará fotografado numa escala
ligeiramente diferente da do ponto b.
:

73. 73
4
4.
.7
7 –
– D
DE
ET
TE
ER
RM
MI
IN
NA
AÇ
ÇÃ
ÃO
O D
DA
A E
ES
SC
CA
AL
LA
A:
:
Algumas companhias de aerofotogrametria costumam colocar no verso da
fotografia a escala aproximada, mas, geralmente, ela precisa ser determinada.
Exemplos de escalas usuais:
Escala
Detalhe
planimétrico
mínimo
Detalhe
altimétrico
mínimo
Exemplo
1:50 000 5 m 1 m Automóvel
1: 20 000 2 m 0,5 m Cultura
1:5 000 0,5 m 0,2 m Homem
4
4.
.8
8 –
– E
ES
ST
TE
ER
RE
EO
OS
SC
CO
OP
PI
IA
A:
:
D
Dá-se o nome de estereoscopia à observação em três dimensões de duas
fotos aéreas consecutivas e que se recobrem parcialmente através de aparelhos
especiais chamados estereoscópios. Cada fotografia de um par fotográfico para
observação ao estereoscópio é uma imagem ligeiramente diferente das mesmas
feições do terreno, as quais podem ser comparadas com as mesmas imagens
recebidas através de cada um dos olhos. Sabe-se que a sensação de
profundidade ou volume que sentimos é devido ao fato de olhar os objetos com
dois olhos. Cada olho registra uma imagem ligeiramente diferente, ver Figura 04.

74. 74
Se um pequeno objeto é segurado a uma distância equivalente a de um braço o
olho direito vê a frente e parte do lado direito, enquanto o esquerdo vê a frente e
parte do lado esquerdo, com mostra a Figura 05. Essas duas imagens são
combinadas pelo cérebro para formar uma visão do objeto em 3D. À medida que o
objeto se afasta, as imagens vão se tornando mais e mais parecidas, diminuindo,
dessa maneira a sensação de relevo.
Para facilitar a sensação de relevo e melhora-la por ampliação, utiliza-se os
estereoscópios, cujo modelo de bolso aparece na Figura 06, esquematizado.
Consta de duas lentes de aumento, cujos centros distam entre si uns 6cm
(distância interpupilar) e cuja a base é colocada paralelamente à linha de vôo das
fotografias já orientadas. O observador olha as fotos através das lentes, obtendo
uma visão ampliada.

75. 75
Nesses estereoscópios as fotos ficam parcialmente sobrepostas, o que
exige dobramento de uma delas na observação de alguns pontos. Esse
inconveniente e removido nos esterioscópios de espelho. O modelo de bolso é
usado em trabalhos de campo e o de espelho, só em escritório, dado seu grande
tamanho.
4. 9 – ÁREA COBERTA POR UMA FOTOGRAFIA AÉREA
Conhecendo a escala e as dimensões de uma fotografia aérea é possível
avaliar a área coberta por esta imagem. A fotografia aérea tem uma dimensão útil
de 23 cm (l).
1) área de cobertura única
2) área de recobrimento longitudinal (RLo)
3) área de recobrimento lateral (RLa)
L = lado da foto
Logo o lado da foto no terreno poderá ser calculado pela seguinte expressão:
•Onde: I = dimensão útil da foto; e
E = escala
Assim, a área coberta pela imagem da foto será:
L = I / E
A = L2

76. 76
A área de cobertura única (sem superposição) de uma fotografia aérea
corresponderia ao produto da dimensão representativa de 70% do lado da foto no
sentido longitudinal e 40% do lado da foto em no sentido lateral. Sendo expressa
por:
Portanto, para avaliarmos a quantidade aproximada de fotos necessárias
para cobrir uma área de 100 km2, por exemplo, basta dividir o valor da área de
interesse pelo valor da área de cobertura única da foto.
REFERÊNCIAS BIBLIOGRAFICAS
BORGES, Alberto Campos. Topografia Aplicada à Engenharia Civil. 2a. Edição
revista e ampliada. Vol. 1, São Paulo: Ed. Edgar Blucher Ltda, 1992.
COMASTRI, José Aníbal. Topografia: Planimetria. 1a. Ed. Viçosa: UFG, 1986.
DOMÉNECH, Francisco Valdés. Topografia. Edições Cetop, 1981.
ESPARTEL, Lélis. Curso de Topografia. 9a. Ed. Rio de Janeiro: Editora Globo,
1987.
LOCH, Carlos. Topografia Contemporânea: Planimetria. Florianópolis: Ed. Da
UFSC, 1995.
LOCH, Carlos. Noções Básicas para a Interpretação de Imagens Aéreas.
Florianópolis: Ed. Da UFSC, 1993.
BORGES, Alberto Campos. Exercícios de Topografia. 3a. Edição
revista e ampliada. São Paulo: Ed. Edgar Blucher Ltda, 2001.
L = 0,28 x A

77. 77
ANEXO I
NOÇÕES DE GPS
(Global Positioning System - Sistema de Posicionamento Global)
1
1.
. I
In
nt
tr
ro
od
du
uç
çã
ão
o:
:
Neste pequeno texto serão abordados os conceitos básicos da tecnologia
conhecida como "GPS", enfocando, em linhas gerais, sem detalhamento ou
aprofundamento, sua história, características e aplicações.
2. Histórico:
As atividades humanas sempre, ou quase sempre, necessitavam e ainda
necessitam se referenciar no espaço, seja esta referência a pequenas extensões
ou a grandes. No primeiro caso (pequenas extensões) o estudo é amparado pelos
conceitos da topografia, ciência aplicada que estabelece as grandezas (ângulos,
distâncias, superfícies, etc.) dentro de seus limites, com confiabilidade e precisão.
Às grandes extensões, acima referidas, podem ser entendidas como o
planeta (a Terra) ou uma considerável área deste, ou seja, grandes dimensões.

78. 78
Em muitas atividades, entre estas várias de engenharia, necessitam conhecer ou
calcular a localização de um ou mais elementos no planeta Terra (podem ser
citados, como exemplos, projetos e obras de estradas, canais, aeroportos,
barragens, etc.). Neste segmento, a posição referenciada é conhecida como
geoposicionamento.
Até há alguns anos, os trabalhos que supriam esta necessidade eram
conhecidos como astronomia de posição, e eram realizados através da
observação de astros celestes naturais com aparelhos óticos mecânicos (o
teodolito de precisão é o melhor exemplo), e, após estudos e cálculos (difíceis e
demorados) ensejavam a posição desejada na Terra.
Durante a II Grande Guerra (anos de 1940), começou-se a utilizar ondas
eletromagnéticas (de rádio) para medir distâncias (na Terra), que auxiliavam no
posicionamento de aviões pela adoção do processo de trilateração eletrônica
(medida dos lados - distâncias - dos triângulos por equipamentos eletrônicos).
Posteriormente, esta tecnologia foi se desenvolvendo e aplicando-se em outros
fins (exemplo: auxílio e posicionamento de embarcações - navios).
A partir de 1957, com o lançamento ao espaço do satélite russo "Sputinik",
iniciou-se a chamada "era espacial", e a técnica de trilateração eletrônica evoluiu
para a trilateração espacial (as medidas das distâncias com ondas
eletromagnéticas passarem a ser feitas não somente entre pontos na Terra, mas
também entre os pontos na Terra e os satélites no espaço).
O primeiro Sistema que utilizava uma constelação de 8 (oito) satélites
artificiais e que tinha como finalidade o geoposicionamento foi o NNSS/Transit
(Navy Navigational Satellite System), desenvolvido pela marinha Norte Americana
durante a década de 1960 e bastante utilizado para fins militares (e em poucos
casos para fins civis), até o início da década de 1990. Este sistema, porém,
possuía dois grandes problemas: 1) Não cobria todo o planeta Terra, 2) havia um
lapso de tempo considerável entre as passagens dos satélites para um mesmo
ponto na Terra, o que ensejava trabalhos demorados.

79. 79
Diante dos problemas do sistema mencionado, as Forças Armadas
Americanas (Marinha e, em especial a Aeronáutica), começaram a trabalhar,
desde 1973, em um outro, que passou a ser conhecido como Sistema
NAVSTAR/GPS, ou simplesmente GPS (Global Positioning System ou ainda,
traduzindo para o português, Sistema de Posicionamento Global).
Os sistema GPS permite posicionar (georreferenciar) qualquer ponto no
Planeta Terra utilizando-se um receptor de sinais de satélites artificias.
Os primeiros satélites foram lançados em 1978, e hoje compõem uma
constelação que cobre toda o planeta e atende tanto a usuários civis quanto
militares.
3. Segmentos do GPS:
Existem três: Espacial; de Controle e de Usuários.
 Segmento Espacial:
Como já exposto, o Sistema GPS provê cobertura mundial (planetária), a
qualquer momento, ou seja, de qualquer ponto da Terra (incluindo os Pólos) são
visíveis (ou rastreáveis) pelo menos quatro satélites visíveis (ou rastreáveis) com
elevação acima de 15° em relação ao horizonte, 24 horas por dia, 365 dias por
ano.
A constelação de satélites ativos é de 24 (vinte e quatro), existindo ainda
alguns de reserva, circulando a Terra em órbitas elípticas (quase circulares),
inclinadas de 55° em relação ao Equador. Existem seis planos orbitais, cujos
intervalos entre si são de 60°. Os satélites estão a uma altitude média de
20.200Km e realizam uma volta na Terra em cerca de 12 horas.

80. 80
Os satélites transmitem duas frequências portadoras, chamadas L1 e L2. A
L1 é modulada por três códigos (C/A, P e D). Enquanto a L2 é modulada somente
pelos códigos P e D.
a) Códigos:
- C/A (Coarse/Acquisition): de acesso livre ou Civil. Provê a base de cálculo
da pseudo distância;
- P (Precise): de uso restrito aos militares e geralmente é incriptado, quado
se torna "Y"
- D: Provê: tempo GPS do satélite (relógio); Dados da órbita do satélite
(efemérides); Dados da saúde do satélite e Dados de correções da Ionosfera. É o
primeiro a ser interpretado pelo receptor
 Segmento de Controle:
Objetivando controlar o sistema, tendo como principais tarefas: determinar
com precisão a órbita de cada satélite; modelagem matemática para predição
destas órbitas; sincronização dos relógios dos satélites; transferências de dados
para cada satélite; correção de posicionamento dos satélite; e lançamento de
novos satélites; etc.
Este enorme sistema operacional consiste de: uma Estação Mestre, cinco
Estações de Monitoramento Mundial e diversas Estações de Controle de Campo:
- Estação Mestre: localizada na Base Falcon da USAF, no Colorado (USA);
- Estações de Monitoramento Mundial:
a) Havaí;
b) Colorado;
c) Ilha de Ascención (Atlântico Sul);

81. 81
d) Diego Garcia (Oceano Índico) e
e) Kwajalein (Oceano Pacífico).
- Estações de Controle de Campo: espalhadas pelo mundo todo, ajudam em
coleta de dados e transmissão dos mesmos às estações de monitoramento
e à estação mestre.
Observação: todos os dados GPS são georreferenciados ao elipsóide
"WGS 84", que é diferente do adotado pelo Sistema Oficial Brasileiro (SAD 69), o
que enseja, via de regra, correções nos rastreamentos realizados.
Deve-se ainda ressaltar que os resultados do posicionamento com GPS,
quando bem realizados os trabalhos e com equipamentos adequados podem ser
muito precisos, porém não estão isentos de erros, falhas e mesmo incorreções
até relativamente grandes, pois se referenciam a uma elipse (WGS 84), e não ao
geoide nem à superfície física da Terra.

 S
Se
eg
gm
me
en
nt
to
o d
de
e U
Us
su
uá
ár
ri
io
os
s:
:
Compreendendo os usuários propriamente ditos, os diversos tipos de
receptores existentes e os vários métodos de posicionamento utilizados.
- Usuários Propriamente ditos:
Podem ser divididos em dois grandes grupos:
a) civis;
b) militares.
- Receptores: Composição Básica: Antena (recebe o sinal), Dispositivo de
rádio-freqüência (identifica o sinal); Microprocessador (executa os cálculos);
Dispositivo para armazenamento de dados (memoriza ou guarda as

82. 82
informações e cálculos); Dispositivo de Controle (teclado/display, etc);
Fontes de alimentação.
- Tipos: Podem ser divididos e sub divididos de diversas maneiras. Serão
abordados, neste texto, dois grandes grupos de divisões ou tipos:
1) Quanto ao tipo de Sinal observado:
a) receptores de pseudo-distância pelo código C/A. Menores, mais simples
e muito mais baratos.
b) receptores do código C/A e das portadoras L1 e L2. Maiores, mais
complexos e muito mais caros.
c) receptores de pseudo-distância pelo código P. Restrito a uso militar.
d) receptores do código C/A, P e das portadoras L1 e L2. São os mais
complexos e caros. Atingem maiores precisões.
2) Quanto ao método de Posicionamento:
a) Absoluto;
b) Diferencias;
c) Relativos ou Interferométricos.
4. Métodos de Posicionamento:
1) Absoluto: também conhecido como "point positioning". Utiliza-se um
receptor, isoladamente, que rastreia, no mínimo, três satélites. Posiciona
utilizando-se a pseudo distância;
2) Diferencial: também conhecido como DGPS. Utilizam-se dois receptores
simultaneamente, sendo um estacionado em um ponto de referência, cujas
coordenadas são conhecidas, e outro estacionado (ou móvel) no(s) pontos(s) que

83. 83
se deseja conhecer as coordenadas. Posiciona utilizando-se a pseudo distância,
porém, de forma muito mais precisa do que o Método Absoluto;
3) Relativo: também conhecido como Interferométrico. Utilizam-se dois
receptores simultaneamente, de forma análoga ao do diferencial, sendo que o
posicionamento não é pela pseudo distância, mas sim pela distância, medida
através de leitura e interpretação e correção não somente dos códigos C/A e P,
mas também e principalmente das fases das portadoras (L1 e L2), que carregam
informações e dados de altíssima precisão e complexidade.
5. Aplicações:
A tecnologia GPS é hoje de grande utilização pela comunidade, tanto no
meio técnico de engenharia como em outras atividades diversas.
- Apoio para levantamentos aerofotogramétricos, aerofotográficos, de
sensoriamento remoto, etc, fundamentais em trabalhos de cadastro, mapeamento
e planejamento, seja no meio urbano ou rural;
- Amarração/referência de coordenadas para projetos e obras de médio e
grande porte;
- Mediadas para controle de grandes áreas, sejam de florestas,
desmatadas, cultiváveis, erodidas, trabalhadas (por exemplo jazidas), etc.;
- Monitoramento de Frotas de veículos;
- Posicionamento para navegação, sejam de embarcações, automóveis,
aviões, etc.
6. OUTROS SISTEMAS:

84. 84
Existem outros sistemas de posicionamento, sendo os mais conhecidos: -
GLONASS (russo), Sistema GALILEU (Europeu) e Sistema Coreano.
Estes sistemas, mais recentemente desenvolvidos, já vem sendo utilizados,
em escala bem menor do que o GPS, por diversos segmentos técnicos, estando
diversos receptores comerciais aptos a receber seus sinais.