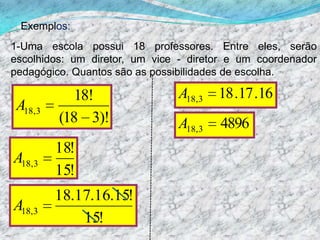
O documento discute permutações e arranjos simples. Ele fornece as fórmulas para calcular o número de permutações simples (Pn = n!) e arranjos simples (An,p) e ilustra seus cálculos com exemplos como anagramas da palavra "LÁPIS" e cargos em uma escola.

1. 3 – Permutação Simples Permutação Simples de n elementos distintos é qualquer grupo ordenado desses n elementos. Para o cálculo do número de permutações simples, usamos: Pn = n!, ou seja, Pn = n.(n – 1).(n – 2)...1 Portanto, o número de permutações simples de n elementos distintos é igual a n fatorial.Pn = n!

2. Exemplo:Vamos calcular o número de anagramas da palavra LÁPIS, lembrando que um anagrama é uma palavra formada com as mesmas letras da palavra dada, podendo ter ou não sentido na linguagem usual .Como a palavra lápis possui 5 letras, bastar calcular:P5 = 5! = 5.4.3.2.1 = 120.

3. Exercício1)Considere a palavra DILEMA e determinar:a)O número total de anagramas65431= 720 anagramas2b)O número de anagramas que começam com a letra D.321451= 120 anagramas

4. c)O número de anagramas que começam com a letra D e terminam com a letra A.411312= 24 anagramasd)O número de anagramas que começam com vogal.335214= 360 anagramas

5. 4 – Arranjo Simples Chama-se arranjo simples todos os agrupamentos simples de p elementos que podem formar com n elementos distintos, sendo p ≤ n cada um desses agrupamentos se difere de outro pela ordem ou natureza de seus elementos. A notação para o número de arranjo simples de n elementos tomados p a p.Fórmula do Arranjo Simples

6. Exemplos:1-Uma escola possui 18 professores. Entre eles, serão escolhidos: um diretor, um vice - diretor e um coordenador pedagógico. Quantos são as possibilidades de escolha.