O documento discute diferentes tipos de flexão em elementos estruturais. Aborda flexão pura, onde apenas momento fletor atua na seção, e flexão combinada, onde momento fletor e esforço cortante atuam simultaneamente. Explica como as tensões variam linearmente na seção transversal em função da distância ao eixo neutro para flexão pura, de acordo com a fórmula de Navier. Também discute como esforços cortantes geram tensões tangenciais adicionais na seção.

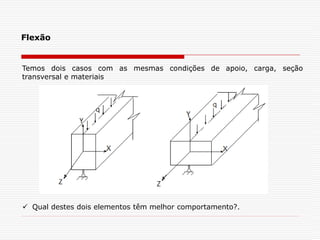
1. Flexão
Temos dois casos com as mesmas condições de apoio, carga, seção
transversal e materiais
 Qual destes dois elementos têm melhor comportamento?.

2. Flexão. Sistemas isostaticos. Tipos de flexão
Em axial vimos como a deformação do elemento linear se reflete com um
encurtamento ou um alongamento. Agora trata-se de uma barra submetida à
ação de cargas, cujo plano de ação passa pelo eixo da barra (YZ).
 Como você considera que se reflete a
deformação em flexão?.
 Se fizermos um corte , que deve surgir na
seção para manter o equilíbrio?.
Observe na figura como todas as cargas são
perpendiculares ao eixo da barra, de tal maneira que
simultaneamente ao momento flector aparece também o
esforço cortante na seção transversal da barra, nesta
situação se chama flexão transversal plana. Observe
como as cargas estão actuando no plano YZ
Lembre que o momento e a resultante das tensãos
normais interiores, distribuídas na seção.

3. Flexão. Sistemas isostáticos. Tipos de flexão
 Que acontece na seguinte situação? Façamos uma seção.
Para manter o equilíbrio aparecerão as forças:
𝑀 = 𝑃 ∙ 𝑍
Secao I-I
𝑃𝑎𝑟𝑎 𝑍 = 0 … . … 𝑀 = 0
𝑃𝑎𝑟𝑎 𝑍 = 𝐿1 … . . 𝑀 = 𝑃 ∙ 𝐿1
Secao II-II
Observe que existe um tramo onde o momento é
constante, nesse tramo se apresenta uma flexão plana
pura. O momento flector é o único esforço interior que
surge na seção transversal da barra.
𝑃𝑎𝑟𝑎 𝑍 = 0 … . … 𝑀 = 0
𝑃𝑎𝑟𝑎 𝑍 = 𝐿1 … . . 𝑀 = 𝑃 ∙ 𝐿1 + 𝐿2 − 𝑃 ∙ 𝐿2=𝑃 ∙ 𝐿1
𝑀 = 𝑃 ∙ 𝐿1 + 𝑍 − 𝑃 ∙ 𝑍

4. Flexão. Sistemas isostáticos. Tipos de flexão
 Que tipo de flexão será esta?
Vamos por parte:
 Qual das duas cargas se corresponde com o
caso anterior?.
 Então que efeito produzira q2 se esta
aplicada no plano horizontal XZ?.
Que passará com a carga “P” que é
excêntrica? vamos localiza-la no centro de
gravidade, em seu eixo longitudinal. Esta
carga vai acompanhada ao transladar-se de
um momento ao redor do eixo Z chamado
(Mz) momento torsor. (plano XY).
Como se pode observar se trata de um
estado de flexão combinada
𝑞2 … … . 𝑀𝑦 ;𝑉𝑋

5. Tomamos a adiante o segundo caso abordado anteriormente (flexão pura). Este
não é o caso mas freqüente na prática, mas por sua simplicidade permite
estabelecer as expressões para o cálculo das tensões.
Flexão plana pura
Seguindo o mesmo orden logico de estudo do esforco axial, o primeiro a fazer
é expor as equações de equilíbrio para calcular σ.

6. Flexão plana pura
Para export o equilibrio é necessario tomar um elemento diferencial de area,
vamos supor 𝜎𝑍 actue nesse diferencial de area, isto implica que a força
resultante e: 𝑑𝐹 = 𝜎𝑍 ∙ 𝑑𝐴
 Qual será as equações de equilíbrio?.
Com estas tres equações é impossível chegar a obter σz , é necessário ir à geometria
da deformada com o objetivo de encontrar equações adicionais. Observe como ao não
ser suficiente as equações de equilíbrio, a seção se converte em hiperestática.
𝐹𝑍 = 𝜎𝑍 ∙ 𝑑𝐴 = 0
𝐴
𝑀𝑦 = 0 𝜎𝑍 ∙ 𝑥 ∙ 𝑑𝐴 = 0
𝐴
(1)
(2)
𝐹𝑋 = 0
𝐹𝑦 = 0
𝑀𝑍 = 0
Não há força em X
Não há força em Y
Não há torcao

7. Tensões normais na flexão.
A determinação das equações geométricas correspondentes ao fenômeno da
flexão pura (distribucao de tensao normales) se pode obter a partir das
hipótese seguintes:
1. As seções transversais da viga, que eram plainas antes de produzir o
fenômeno da flexão, continuam sendo plainas depois que este ocorre e só
giram um certo ângulo ao redor de um eixo que é perpendicular ao eixo da
barra.
2. As fibras longitudinais da viga não se pressionam entre si, por isso depois
de produzir o fenômeno seguem sendo paralelas entre elas.
3. As fibras longitudinais, quando se produz a flexão, umas se comprimem e
outras se traccionan, existindo umas centrales que nem se alargam nem se
cortam, conformando uma superficie neutra. (a intercessão destas fibras que
nem se alargam nem se cortam com a seção transversal da viga constituem a
Linha Neutra da seção). Nesta linha no existe nenhuma tensoe sobre ela.
Estas hipotesis são validas para elementos magros que sofrem pequenas
deformações, onde a única componente normal σz é não nula (esfuerzo
uniaxial). Nao há distorção.

8. Tensões normais na flexão.
Considerando o arco J-K, localizado a uma
distância “Y” sobre a superfície neutra:
Como estamos en torno das pequenas
deformacoes pode-se procurar uma relaçãoentre
“L” “𝜌" 𝑒 "𝜃"
Onde:
𝜌: radio de curvatura. Reflete a posiçãoda superficie neutra.
y: reflete a posiçãodas fibras longitudinales J-K com relaçãoa superficie neutra.
tan 𝜃 =
𝐿
𝜌
Como 𝛳 es pequena: 𝐿 = 𝜌 ∙ 𝜃
𝐿′
= 𝜌 − 𝑦 ∙ 𝜃
𝜀𝑍 =
∆𝐿
𝐿
=
𝑙𝑜𝑛𝑔 𝑓𝑖𝑛𝑎𝑙 − 𝑙𝑜𝑛𝑔 𝑖𝑛𝑖𝑐𝑖𝑎𝑙
𝑙𝑜𝑛𝑔 𝑖𝑛𝑖𝑐𝑖𝑎𝑙
=
𝐿′
− 𝐿
𝐿
𝜀𝑍 = −
1
𝜌
∙ 𝑦 (3)

9. Tensões normais na flexão.
 Que significa o signo negativo na equação da deformada?
 Manteria-se este signo se se tivesse feito a análise com fibras longitudinais se
localizadas por debaixo da superfície neutra?.
Ja temos a equacoes de
equilibrio:
𝑀𝑋 = 0 𝑀𝑋 = −𝜎𝑍 ∙ 𝑦 ∙ 𝑑𝐴
𝑀𝑦 = 0 𝜎𝑍 ∙ 𝑥 ∙ 𝑑𝐴 = 0
𝐴
𝐹𝑍 = 𝜎𝑍 ∙ 𝑑𝐴 = 0
𝐴
E a geometrica: 𝜀𝑍 = −
1
𝜌
∙ 𝑦
Seguindo a mesmo ordem de esforco axial, que equação esta faltando?
(3)
(1)
(2)
Quando 𝜀𝑍 < 0 que corresponde a uma compressão, enquanto quando 𝜀𝑍> 0
corresponde a uma tração.

10. Tensões normais na flexão, fórmula do Navier
Partindo do fato de que cada uma das fibras longitudinais se encontra
submetida a tração ou compressão, conforme se alargue ou se corte, então, de
acordo com a Lei do Hooke, as tensões normais que nas mesmas ocorrem
serão:
Substindo equação (3) : em (4), se obtem:
Já aqui se pode falar da lei de distribução lineal de tensõe. A variável é “y”
porque dá a posição de qualquer fibra com relação à neutra .
A expressão (5) é a Equação Física correspondente ao fenômeno da flexão
pura. Dita expresao não é explicita. Ainda não se localizou a lineia neutra na
seção e por tanto não tenho como obter ρ. Por isso se precisa retomar
novamente as equaçoes de equilíbrio da seção, como se indica a seguir.
(4)
(5)
𝜎𝑍 = 𝐸 ∙ 𝜀𝑍
𝜎𝑍 = −𝐸 ∙
𝑦
𝜌
𝜀𝑍 = −
1
𝜌
∙ 𝑦
Primera equação de tensão de
um elemento sometido a
flexao

11. As tensões normais variam, segundo a altura
da seção transversal, proporcionalmente à
distância do eixo neutro. As tensões máximas
terão lugar nos borde, superior e inferior, da
seção.
Sustituindo equação (5): em (2):
𝜎𝑍 = −𝐸 ∙
𝑦
𝜌
𝐹𝑍 = 𝜎𝑍 ∙ 𝑑𝐴 = 0
𝐴
𝐹𝑍 = −
𝐸
𝜌
𝑦
𝐴
∙ 𝑑𝐴=0
Tensões normais na flexão, fórmula do Navier
Como
𝐸
𝜌
nao podeser diferente de 0, quem tem que ser igual a 0 e 𝑦
𝐴
∙ 𝑑𝐴
Sustituindo (5): en (1):
(6)
𝑀𝑋 = +
𝐸
𝜌
𝑦2
∙ 𝑑𝐴
𝐴
𝜎𝑍 = −𝐸 ∙
𝑦
𝜌
(7)
 Que significa a condição 𝑦
𝐴
∙ 𝑑𝐴? . E se toma o valor 0?
Quando o momento estatico é igual a 0, el eixo X passa pelo centroide, o que
implica que a lineia neutra coincide com o eixo centroidal da seção.

12. Como se conhece que o momento de inércia com respeito ao eixo centroidal é:
Sustituindo a equacão (8) em (7):
𝐼𝑋 = 𝑦2
∙ 𝑑𝐴
𝐴
𝑀𝑋 =
𝐸
𝜌
∙ 𝐼𝑋
(8)
(9)
Tensões normais na flexão, fórmula do Navier
1
𝜌
=
𝑀𝑋
𝐸 ∙ 𝐼𝑋
Sustituindo (9) em (5): 𝜎𝑍 = −𝐸 ∙
𝑦
𝜌
𝜎𝑍 = −
𝑀𝑋 ∙ 𝑦
𝐼𝑋
(10)
Esta expressão constitui a FORMULA DE NAVIER para o cálculo das tensões
normais durante o fenomeno da flexão pura. Note-se nela que a distribução
de tensões na seção e lineal.
𝑀𝑋 = +
𝐸
𝜌
𝑦2
∙ 𝑑𝐴
𝐴

13. Modulo da secao
Do ponto de vista prático se acostuma a expor
o cálculo de σ do seguinte modo: Suponha-se
uma seção genérica submetida a flexão plana
como se mostra na figura, os Yc e Yt representam
as distâncias das fibras longitudinais extremas
submetidas a compressão e tração
respectivamente então se pode agrupar
estes términos com o parâmetro inércia da
seção com respeito ao eixo centriodal e eixo neutro
por corresponder tanto os Y como a inércia a
características geométricas da seção em estudo
aparecendo outra característica denominada modulo
da seção à flexão(ω), quer dizer:
ωc = Ix/yc e ωt = Ix/yt
Então a expressão de tensão normais
para valores extremos se pode expor desta forma:
σmáxc= Mmáx/ωc e σmáxt= Mmáx/ω t.

14. Flexão transversal plana
Suponhamos que temos uma viga em voladizo (extremo
livre) feitas de pranchas separadas que se sujeita em
um extremo, composta por um material não
homogeneo.
 Que acontece com as pranchas?.
Por isso neste caso terá que falar de esforços cortante não só em planos
verticais transversais mas também em planos longitudinais horizontais.
Suponhamos a mesma viga mas agora se trata de um
elemento homogeneo, que tem uma longitude “L” e
vamos fazer lhe um corte em “C”. Mantemo-nos em um
plano vertical e a viga é simétrica.
 Que forcas interiores se geram?.
𝑀𝑥 = 𝑃 ∙ 𝑧
(1)

15. Substitindo (1) na formula de Navier: 𝜎𝑍 = −
𝑀𝑋 ∙ 𝑦
𝐼𝑋
Observe como as tensoes dependem no so do
momento, mas também da localização
𝜎𝑍 =
𝑃 ∙ 𝑧
𝐼𝑋
∙ 𝑦
A aparição dos esforços cortantes se supõe que não altera a distribuição das
tensões normais obtidas pelo Navier para o caso de flexão pura, porque se
trata de elementos primaticos de pequena relação espessura - comprimento. As
vigas a partir desta hipótese são as conhecidas como Vigas Simples e não de
parede como também podem aparecer na prática as quais têm outro tratamento
teórico. A seguidas se desembrulha a análise para dita viga com a aparição dos
esforços cortantes associados.
Flexão transversal plana

16. Determinação das tensões tangenciais durante o fenômeno da
flexão
Retomemos a mesma seção transversal utilizada na flexão pura. Continuemos
com e plano vertical respeito ao qual a barra é simétrica e vamos tomar o
elemento diferencial.
𝑑𝐹𝑦 = 𝜏𝑌𝑍 ∙ 𝑑𝐴
𝑑𝐹𝑋 = 𝜏𝑋𝑍 ∙ 𝑑𝐴
Agora vamos a definirque magnitudes
tem estascomponentes: 𝜏𝑌𝑍 e 𝜏𝑋𝑍
Nos procesos anteriores se procurabam las equações de equilibrio, geometrica e
fisica, mas neste caso el proceso e diferente.

17. Determinação das tensões
Comencemos por la equação de equilibrio ja conhecidas:
Mas quedam três equaciones que estan relacionadas com 𝜏
𝐹𝑋 = 0
𝐹𝑌 = 0
𝑀𝑧 = 0
𝜏𝑋𝑍 ∙ 𝑑𝐴 = 0
𝐴
𝜏𝑌𝑍 ∙ 𝑑𝐴 = −𝑉
𝐴
Não há nenhum
cortante paralelo ao
eixo X.
equação trivial, não se conhece nada
Nas caras superiores e inferiores as tensões tangenciais é igual a 0 porque
ninguém desliza na fibras superiores e inferiores.
Como a análise é em uma viga simples, aplica-se a expressão do Navier para
calcular as tensão normal (𝜎𝑍). Mantém−se então a mesma distribuição de
tensões normais declarada em flexão pura quando se aplica a carga P.

18. Há uma relação entre as tensões tangenciais no plano que são
perpendiculares. Para demonstrar o anterior se toma uma porção interior
coincidente com o plano vertical de simetria, como se mostra na figura.
Estabelecendo momento com respeito a O:
𝑀𝑜 = 𝜏𝑌𝑍 ∙ 𝑑𝑌 ∙ 1 ∙
𝑑𝑍
2
− 𝜏𝑍𝑌 ∙ 𝑑𝑍 ∙ 1 ∙
𝑑𝑌
2
=0
𝜏𝑍𝑌 = 𝜏𝑌𝑍 Lei de pariedad de tensões tangenciais
Como conclusao pode dizer-se que as tensões tangenciais em planos
perpendiculares são iguales en magnitud y giran en sentido contrario.
Determinação da distribução dos esforcos cortantes (𝝉𝒀𝒁 )

19. Nos casos de barras submetidas a força axial e flexão pura foi conveniente o
análise das deformações correspondentes à carga, mas como as deformações
referidas às cargas transversais é complexa se utiliza uma aproximação
diferente. Quer dizer que neste caso não se seguira no adiante o mesmo orden
logico de estudo do esforco axial e flexao pura. En outra palavra, agora
corresponderia la geometria da seção, no entanto continuamos com el analises
del equilibrio, de modo que partiendo das tensões em planos horizontais e sua
relação em planos verticais (90º), se chegara a expressão geral para o calculo
de ditas tensões.
Suponha a mesma viga e vamos fazer um corte en A’-C’, separada da lineia
neutra (LN) uma magnitude Y1
Determinação dos esforcos cortantes (𝝉𝒀𝒁 )

20. Vamos separar ou corte. Cortamos-se tem que aparecer tensões normais, o
qual implica que tem que aparecer uma força horizontal cortante (H) para
equilibrar a força de tensão resultante de tensão normal
Ao supor que a distribuição de esforços normais em uma seção transversal
dada não se afeta pelas causadas por esforços cortantes, como foi dito
anteriormente, e se se conhece que:
𝜎𝑍 ∙ 𝑑𝐴 =
𝑃 ∙ 𝑍 ∙ 𝑦
𝐼𝑋
∙ 𝑑𝐴
𝜎𝑍 =
𝑀𝑋∙𝑦
𝐼𝑋
=
𝑃∙𝑍∙𝑦
𝐼𝑋
Determinação dos esforcos cortantes (𝝉𝒀𝒁 )
(1)
Então se podeestabelecerque la resutante de esa tensões (𝜎𝑍) e:

21. Para que haja um equilíbrio:
𝐻 =
𝑃 ∙ 𝑍
𝐼𝑋
𝑦 ∙ 𝑑𝐴
𝑌=𝐶
𝑦=𝑌1
𝑦 ∙ 𝑑𝐴
𝑌=𝐶
𝑦=𝑌1
= 𝑆𝑥
A integral momento estático da área que está entre Y=Y1 e Y=C
(área com pontos),
𝐻 =
𝑃 ∙ 𝑍 ∙ 𝑆𝑋
𝐼𝑋
Determinação dos esforcos cortantes (𝝉𝒀𝒁 )
𝐴 : Área da porção com pontos.
𝑌: Distancia desde seu centroide até a LN
Então a expresao (2) fica como:
Sendo: 𝑆𝑥=𝐴 ∙ 𝑌
(2)
(3)

22. Determinação dos esforcos cortantes (𝝉𝒀𝒁 )
Observe na expressão (3) como o cortante (H) é proporcional a Z , então se pode
dizer:
𝐻
𝑍
=
𝑃 ∙ 𝑆𝑋
𝐼𝑋
(4)
Tem-se então:
𝑞 =
𝑃∙𝑆𝑋
𝐼𝑋
=
𝑉∙𝑆𝑋
𝐼𝑋
Exercicio:
Uma viga esta feita de três planchas de 20x100 mm, as quales se unen com
pregos. Se entre os pregos há uma separação de 25mm e a força cortante na
viga é V=500 N, ache a força cortante em cada prego
(5)
Chegando a encontrar uma força por unidade de
longitude ou fluxo de cortante (q)

23. Determinação dos esforcos cortantes (𝝉𝒀𝒁 )
Agora ja tamos em condicões de chegar a expresão de tensões tangenciais.
 Como podemos expressar ∆𝐻 em funcão de
fluxo de cortante ∆Z?
∆𝐻 = 𝑞 ∙ ∆𝑍=
𝑉∙𝑆𝑋
𝐼𝑋
∙ ∆𝑍
∆𝐻 = 𝑞 ∙ ∆𝑍 (6)
Substituindo (5) en (6)
(7)
Dividiendo (7) entre ∆𝐴 = 𝑡 ∙ ∆𝑍 , se obtem o valor medio de 𝜏𝑍𝑌 , o qual e
igualsegundo o principio de pariedad a 𝜏𝑌𝑍
∆𝐻
∆𝐴
= 𝜏𝑚𝑒𝑑𝑖𝑜 𝑌𝑍 =
𝑉 ∙ 𝑆𝑋
𝐼𝑋 ∙ 𝑡
Fórmula do Shuravskii para a determinação
das tensões tangenciais que surgem durante
o fenômeno da Flexão Transversal em vigas
simples
(8)

24. Determinação dos esforcos cortantes (𝝉𝒀𝒁 )
Sempre que o largo de viga seja pequena em comparação com a altura, o
esforço cortante varia so suavemente ao longo de C1’ e C2’ e se pode usar a
equação (8) para calcular 𝜏 𝑌𝑍. Em realidade 𝜏 𝑌𝑍 é major nos pontos C1’ e C2’
que em C’
 Porque os valores são maiores nos extremo??
Para valores grandes de b/h, 𝜏𝑚𝑎𝑥 em C1e C2 pode ser muitas vezes maior que
o valor médio calculado com o passar do eixo neutro. Nestes casos se deve
trabalhar com os valores que se mostram na tabela seguinte

25. Determinação dos esforcos cortantes (𝝉𝒀𝒁 )
b/h 0,25 0,5 1 2 4 6 10 20 50
𝜏𝑚𝑎𝑥/𝜏𝑚𝑒𝑑𝑖𝑎 1,0008 1,033 1,126 1,396 1,988 2,582 3,77 6,74 15,65
𝜏𝑚𝑖𝑛/𝜏𝑚𝑒𝑑𝑖𝑎 0,983 0,94 0,856 0,805 0,8 0,8 0,8 0,80 0,8

26. Vamos a voltar a seção transversal rectangular. Neste caso t=b.
𝑌 =
𝐶−𝑌
2
+Y=
1
2
𝐶 + 𝑌
𝐼𝑋 =
𝑏∙ℎ3
12
=
2
3
∙ 𝑏 ∙ 𝐶3
𝑆𝑋=A∙ 𝑌 =
1
2
∙ 𝑏 ∙ 𝐶2
− 𝑌2
𝜏 𝑌𝑍 =
𝑉 ∙ 𝑆𝑋
𝐼𝑋 ∙ 𝑡
Substituindo em (8)
𝜏 𝑌𝑍 =
3
4
∙
𝑉 ∙ 𝐶2
− 𝑌2
𝑏 ∙ 𝐶3
(9)
Se obtem:
É necessário sublinhar, que pela fórmula do
Zhuravski se calculam as tensões tangenciais que
são paralelas à força cortante, quer dizer, em nosso
caso a tensões verticais

27. Como: 𝐴 = 𝑏 ∙ 2𝐶 , a expresão (9) fica:
𝜏 𝑌𝑍 =
3
2
∙
𝑉
𝐴
∙ 1 −
𝑌2
𝐶2
(10)
Quando Y=0 𝜏 𝑌𝑍 𝑚𝑎𝑥 =
3
2
∙
𝑉
𝐴
Esforços cortantes 𝝉𝒀𝒁 em tipos de vigas de seção retangular magra
Lei de distribuição das tensões
na seção de uma viga
retangular. Está lei se
determinada pela variação do
Sx, já que as outras
magnitudes para a seção dada,
permanecem constantes.

28. Resumo
No caso geral da flexão (flexão transversal), nas seções transversais da barra
surgem momentos flectores e forças cortantes. A existência Mf esta relacionada
com a aparição nas seções transversais de tensões normais, que se calculam
pela fórmula do Navier. A existência da força cortante está relacionada com o
surgimento de tensões tangenciais segundo a lei de reciprocidade destas
tensões: Tensões análogas surgem nas seções longitudinais da barra.
O surgimento de tensões tangenciais vai acompanhado da aparição de
deslizamentos, e, como resultado destes, as seções transversais da viga deixam
de ser plainas (deixa de ser válida a hipótese do Bernoulli). Durante a flexão
transversal da barra surgem também tensões nas seções longitudinais da barra,
quer dizer que as fibras pressionam as umas sobre as outras.
Para achar as tensões tangenciais, a partir da colocação das equações de
equilíbrio, obtém-se a equação do Zhuravsky.

29. Exercicio
A viga que se mostra tem uma seção transversal T construída com
pranchas de aço. Calcule a distribuição de tensões normais e
tangenciais na seção transversal acima do apoio intermedio.

30. Exercicio
A viga que se mostra tem uma seção transversal T construída com pranchas
de aço. Calcule a distribuição de tensões normais e tangenciais na seção
transversal do centro.