A Regra de Simpson fornece uma aproximação melhor do que a Regra dos Trapézios ao considerar um polinômio interpolador de grau 2 em vez de grau 1. A Regra de Simpson simples calcula a integral como a soma de três termos ponderados pelos pontos a, c, e b. A Regra de Simpson composta aplica a regra simples em subintervalos para obter uma aproximação ainda melhor.

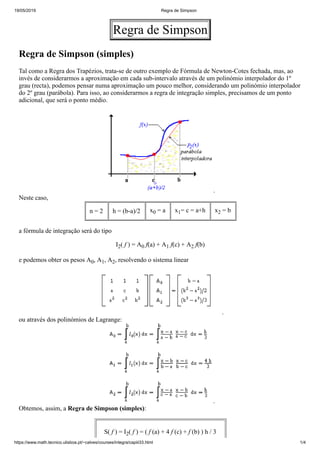
1. 19/05/2019 Regra de Simpson
https://www.math.tecnico.ulisboa.pt/~calves/courses/integra/capiii33.html 1/4
Regra de Simpson
Regra de Simpson (simples)
Tal como a Regra dos Trapézios, trata-se de outro exemplo de Fórmula de Newton-Cotes fechada, mas, ao
invés de considerarmos a aproximação em cada sub-intervalo através de um polinómio interpolador do 1º
grau (recta), podemos pensar numa aproximação um pouco melhor, considerando um polinómio interpolador
do 2º grau (parábola). Para isso, ao considerarmos a regra de integração simples, precisamos de um ponto
adicional, que será o ponto médio.
.
Neste caso,
n = 2 h = (b-a)/2 x0 = a x1= c = a+h x2 = b
a fórmula de integração será do tipo
I2( f ) = A0 f(a) + A1 f(c) + A2 f(b)
e podemos obter os pesos A0, A1, A2, resolvendo o sistema linear
.
ou através dos polinómios de Lagrange:
.
Obtemos, assim, a Regra de Simpson (simples):
S( f ) = I2( f ) = ( f (a) + 4 f (c) + f (b) ) h / 3

2. 19/05/2019 Regra de Simpson
https://www.math.tecnico.ulisboa.pt/~calves/courses/integra/capiii33.html 2/4
Erro da Regra de Simpson (simples)
Neste caso, usamos um polinómio interpolador do 2º grau, e sabemos da fórmula do erro de interpolação
que:
f (x) - p2 (x) = f [ a, b, c, x ] (x - a) (x - b) (x - c)
portanto
.
No entanto, aqui não podemos aplicar directamente o teorema do valor intermédio para integrais, porque (x-
a)(x-b)(x-c) muda de sinal no intervalo [a, b].
Introduzindo um ponto auxiliar d pertencente ao intervalo [a, b], podemos usar a definição de f [ a, b, c, d, x ]
para obter
f [ a, b, c, x ] = f [ a, b, c, d ] + f [ a, b, c, d, x ] ( x - d )
Substituimos esta expressão no integral, como
obtemos, fazendo d tender para c, e aplicando o teorema do valor intermédio para integrais, porque (x-a)(x-b)
(x-c)2 já não muda de sinal no intervalo [a, b]:
admitindo que a função f está, pelo menos, em C4[ a, b ].
(Observamos que a repetição dos nós nas diferenças divididas leva a expressões mal definidas, que são
indeterminações, pelo que esta notação só faz sentido como um limite, sabendo que a função f é
diferenciável.
Por exemplo:
recursivamente, através da definição de diferenças divididas, podemos obter uma expressão em função de f [
c, c ] = f ' (c) ).
Portanto, se f pertence a C4[ a, b ], o Erro da Regra de Simpson (simples) fica:
Observação:
Por construção, sabiamos que a Regra de Simpson era exacta para polinómios do 2º grau, mas esta fórmula

3. 19/05/2019 Regra de Simpson
https://www.math.tecnico.ulisboa.pt/~calves/courses/integra/capiii33.html 3/4
do erro revela-nos que ela é exacta mesmo para polinómios do 3º grau!
Portanto, enquanto que a Regra dos Trapézios tem apenas grau 1, a Regra de Simpson tem grau 3.
Regra de Simpson (composta)
Regra de Simpson aplicada a dois sub-intervalos.
Convém referir que, enquanto a Regra dos Trapézios composta corresponde a fazer a aproximação da função
integranda através de um spline linear, no caso da Regra de Simpson composta, a aproximação feita não
corresponde a um spline de grau 2, pois não exigimos regularidade da derivada nos nós. Essa regularidade
não é necessária quando integramos. Aliás, geometricamente depreende-se que, exigir a regularidade da
função aproximadora, nos nós, não traz aparentes vantagens para a aproximação da área delimitada pelo
gráfico da função...
Para aplicar a regra de Simpson usando sub-intervalos, devemos considerar um número impar de nós N+1,
de forma que ao dividirmos o intervalo [ a, b ] em N/2 sub-intervalos, obtemos os nós
xi = a + i h
para i = 0, ..., N, com h = (b - a)/N.
Assim, podemos considerar três nós em cada sub-intervalo [ x2k-2, x2k ] :
x2k-2, x2k-1, x2k
para k = 0, ..., N/2, e aplicamos a regra de Simpson simples a cada um destes sub-intervalos.
Como
obtemos
e simplificando os termos repetidos, temos a Regra de Simpson Composta:
Erro da Regra de Simpson Composta

4. 19/05/2019 Regra de Simpson
https://www.math.tecnico.ulisboa.pt/~calves/courses/integra/capiii33.html 4/4
Tal como no caso da Regra dos Trapézios composta, o erro da Regra de Simpson composta, resulta da soma
dos erros em cada sub-intervalo, ou seja:
a partir desta expressão, e de forma análoga, obtemos, a Fórmula do Erro para Regra de Simpson
Composta: