I) O documento fornece um conjunto de exercícios matemáticos para os alunos do 6o ano completarem durante as férias de inverno. II) Instruções importantes incluem realizar os exercícios com antecedência, tirar dúvidas antes da data de entrega, e enviar os resultados na plataforma online. III) Os exercícios variam em tópicos como números primos, porcentagens, frações e expressões algébricas.

1. Winter Break - 2016 Homework – Trabalho de Férias 2016 – 6º ano
ATENÇÃO :
I) Algumas questões estão parametrizadas, é importante conferir os dados com o problema base da
lista a seguir pois esses podem ser modificados para seu preenchimento na plataforma zoomapp.
II) Faça os exercícios com antecedência e pesquise e tire suas dúvidas evitando acúmulo antes do
prazo final.
III) Preencha seus dados finais na plataforma e envie ao terminar todos os problemas. Para isso
disponibilizamos essa lista para trabalho.
IV) Caso encontre alguma divergência ou dificuldade operacional use o ”posso ajudar” da plataforma.
V) Mantenha todas as suas anotações consigo para tirar suas dúvidas ou depois.
1. Qual das alternativas abaixo indica uma afirmação verdadeira?
a) Todo múltiplo de 7 é um número ímpar.
b) Todo número ímpar é múltiplo de 7.
c) Todo número par é múltiplo de 8.
d) Todo múltiplo de 8 é um número par.
2. (CMRJ) Usei um terço do meu salário para pagar a parcela do meu apartamento, metade do que sobrou para
pagar o plano de saúde, um quarto do que sobrou para pagar as compras de mês e um terço do que sobrou para
pagar o telefone. Se, após o pagamento dessas contas, sobraram R$95,00, meu pagamento foi de:
a) R$2280,00
b) R$1140,00
c) R$760,00
d) R$570,00
e) R$380,00
3. Qual é a soma dos nove primeiros números naturais primos?
a) 87
b) 89
c) 93
d) 100
4. A soma dos quadrados dos três menores números primos vale
a) 14.
b) 38.
c) 64.
d) 72.
e) 100.
5. Um pesquisador tem à disposição quatro frascos com a mesma substância. No frasco I, há um quarto de litro
dessa substância; no frasco II, há um quinto de litro dessa substância; no III, há um oitavo de litro dessa
substância; e no frasco IV há um décimo de litro da substância. Se ele utilizar os dois frascos que mais contêm
dessa substância, ele terá utilizado, ao todo:
a) dois nonos de litro.
b) dois dezoito avos de litro.
c) nove vinte avos de litro.
d) nove quarenta avos de litro.
e) um nono de litro.
6. Qual é o valor da expressão numérica
1 1 1 1
5 50 500 5000
   ?
a) 0,2222
b) 0,2323
c) 0,2332
d) 0,3222

2. Winter Break - 2016 Homework – Trabalho de Férias 2016 – 6º ano
7. Considere os conjuntos X e Y definidos por 𝑋 = {𝑥 ∈ ℕ 𝑥⁄ é 𝑚ú𝑙𝑖𝑝𝑙𝑜 𝑑𝑒 3} 𝑒 𝑌 = {𝑦 ∈
ℕ 𝑦⁄ é 𝑑𝑖𝑣𝑖𝑠𝑜𝑟 𝑑𝑒 84}
Sobre o conjunto A X Y,  é correto afirmar que
a) se n A então ( n) A. 
b) o conjunto A possui 4 elementos.
c) o menor elemento do conjunto A é o zero.
d) o maior elemento do conjunto A é divisível por 7.
8. (EPCAR) Numa turma de x alunos,
2
3
são atletas e suas preferências por modalidades esportivas estão
expressas no gráfico abaixo.
Considerando que nenhum desses alunos pratica mais de um esporte, analise as afirmativas abaixo, classificando-
as em V (verdadeira) ou F (falsa).
( ) Metade dos atletas gosta de vôlei ou de basquete.
( ) 40% dos atletas preferem futebol.
( ) O número de alunos desta turma é menor que 25
Tem-se a sequência correta em
a) F - F - F
b) V - V - V
c) F - V - F
d) V - F - V
9. Para encher um reservatório de água, estão conectadas a ele duas torneiras com vazões diferentes. A primeira
torneira enche esse reservatório em 15 horas e, a segunda, em 10 horas.
Qual a fração, em relação à capacidade total do reservatório, representaria a quantidade de água eliminada pelas
torneiras se elas ficassem abertas ao mesmo tempo, durante 2 horas?
Assinale a alternativa CORRETA.
a) 1 3
b) 2 25
c) 1 150
d) 1 6
e) 2 15
10. Um móvel de R$ 360, 00 deveria ser comprado por um grupo de rapazes que contribuíram em partes iguais.
Como 4 deles desistiram, os outros precisaram aumentar a sua participação em R$ 15, 00 cada um.
Qual era a quantidade inicial de rapazes?
a) 8

3. Winter Break - 2016 Homework – Trabalho de Férias 2016 – 6º ano
b) 12
c) 15
d) 20
11. (Vunesp) Duas empreiteiras farão conjuntamente a pavimentação de uma estrada, cada uma trabalhando a
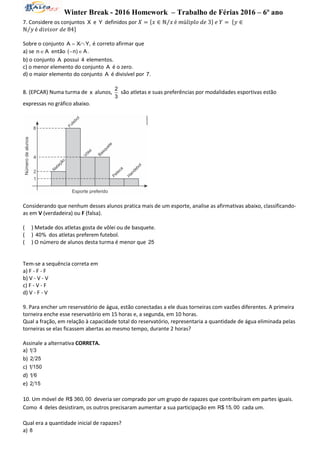
partir de uma das extreminadades. Se uma delas pavimentar 2/5 da estrada e a outra os 81 km restantes, a
extensão dessa estrada é de:
a) 125 km
b) 135 km
c) 142 km
d) 145 km
e) 160 km
12. (PUC-MG) O valor da expressão a seguir é:
1
1
2 ÷ (
3
2)
2
1
3
−
1
6
a) 4
b) 2
c) 1/3
d) 1/9
e) 81/4
13. Um tanque contém água até seus 2/3. Colocando-se mais 36 litros de água ele ficará com ¾ de sua
capacidade. A capacidade do taque é de:
a) 432 litros
b) 360 litros
c) 54 litros
d) 48 litros
14. Calcule o valor da soma dos resultados das expressões a seguir:
𝐼)
[(3 −
1
2)
2
−
3
4] × [
3
4 × (
2
3)
3
]
2
9
𝐼𝐼)
7
4 − {2 − [
2
5
×
1
2 −
1
10] + (
1
2)
2
}
1
10
a) uma dúzia
b) uma dezena
c) duas dezenas
d) meia dezena
15. Tomei no almoço a metade de uma garrafa de vinho e no jantar tomei a metade do que sobrou. Então podemos
afirmar que a fração do líquido que restou na garrafa foi:
a)
1
4
b)
1
3
c)
1
8
d)
1
2
16. Um pedreiro foi contratado para construir um muro. No primeiro dia de serviço ele construiu um oitavo de
muro e, no segundo dia, o triplo do que havia construído no primeiro dia. Dessa forma, nos dois primeiros dias ele
construiu:
a) o muro inteiro.

4. Winter Break - 2016 Homework – Trabalho de Férias 2016 – 6º ano
b) a metade do muro.
c) mais da metade do muro.
d) menos da metade do muro.
17. Um recipiente com 24 litros de vinho foi distribuído em garrafas, cada uma com capacidade de
3
4
de litro. Se
cada garrafa serve 6 taças, o número de taças que podem ser servidas é de:
a) 24
b) 108
c) 144
d) 192
18. Uma pessoa realizou uma viagem de 1200km da seguinte maneira: os primeiros
3
8
do percurso foram feitos de
ônibus. os
7
12
seguintes, de trem; e o restante, de automóvel. A distância que essa pessoa andou de automóvel foi:
a) 50 km
b) 100 km
c) 500 km
d) 1150 km
19. O corpo de bombeiros de determinada cidade, em um ano, prestou assistência a diversas vítimas de acidentes.
Entre essas vítimas,
1
3
sofreu queimaduras,
5
12
sofreu intoxicação e
1
4
sofreu, simultaneamente, queimaduras e
intoxicação.
Do total de vítimas assistidas, a fração que representa a quantidade de pessoas que não sofreram
queimaduras nem intoxicação é igual a:
a)
1
4
b)
1
3
c)
1
2
d)
2
3
20. O valor da expressão √
36
25
: (
1
2
)
4
é:
a)
48
5
b)
96
5
c)
12
5
d)
24
5
21. (OBM) Num quadrado formado por 9 quadrados menores e do mesmo tamanho, queremos escrever um X e
um O, de forma que eles não fiquem vizinhos, isto é, os quadrados em que se encontram não podem ter
um lado ou um vértice comum. O desenho abaixo mostra uma dessas possibilidades:

5. Winter Break - 2016 Homework – Trabalho de Férias 2016 – 6º ano
De quantas maneiras podemos localizar os dois sinais, respeitadas as condições apresentadas?
a) 32 b) 20 c) 64 d) 18 e) 12
22. Um jogo consiste em partir da casa 1 à casa 36 numa trilha com casas numeradas de 1 a 36. Os dois jogadores
começam na casa 1 e o avanço de casas depende do lançamento de dois dados cúbicos comuns.
- Se a soma dos pontos for par, o jogador avança 3 casas.
- Se a soma dos pontos for ímpar, o jogador avança 1 casa.
- Se o jogador ultrapassar a última casa, retorna à casa 1.
- A ordem com que os jogadores iniciam suas jogadas é definida por alguma forma de sorteio.
Ganha quem parar primeiro na casa 36.
O menor número de jogadas que alguém pode fazer e ganhar é
a) 37 b) 13 c) 12 d) 14 e) 17
23. (OBM) A fortuna de João foi dividida da seguinte forma: um quinto para seu irmão mais velho, um sexto do
restante para seu irmão mais novo e partes iguais do restante para cada um de seus 12 filhos. Que fração da fortuna
cada filho recebeu?
a)
20
1
b)
18
1
c)
16
1
d)
15
1
e)
14
1
24. (OBM) Quatro carros, de cores amarela, verde, azul e preta, estão em fila. Sabe-se que o carro que está
imediatamente antes do carro azul é menor do que o que está imediatamente depois do carro azul; que o carro
verde é o menor de todos; que o carro verde está depois do carro azul; e que o carro amarelo está depois do preto.
O primeiro carro da fila:
a)é amarelo. b)é azul. c)é preto. d)é verde.
e) não pode ser determinado apenas com esses dados.
OBS: O primeiro da fila é o que vem antes de todos os outros.
25. (OBM) 64 jogadores de habilidades diferentes disputam um torneio de tênis. Na primeira rodada, são feitos 32
jogos (os emparelhamentos são por sorteio), e os perdedores são eliminados. Na segunda rodada, são feitos 16
jogos, os perdedores são eliminados, e assim por diante. Se os emparelhamentos são feitos por sorteio e não há
surpresas ( se A é melhor que B, A vence B), qual o número máximo de jogos que o décimo melhor jogador consegue
jogar?
a)2 b)3 c)4 d)5 e)6
26. (OBM) Se p e q são naturais tais que
15
11
q
p
10
7
 , o menor valor que q pode ter é:
a)6 b)7 c)25 d)30 e)60
27. (OBM) Em certo país, a unidade monetária é o pau. Há notas de 1 pau e moedas de meio pau, um terço de pau,
um quarto de pau e um quinto de pau. Qual a maior quantia, em paus, que um cidadão pode ter em moedas sem
que possa juntar algumas delas para formar exatamente um pau?
a)
12
11
b)
12
5
1 c)
15
7
2 d)
60
13
2 e)
60
43
2

6. Winter Break - 2016 Homework – Trabalho de Férias 2016 – 6º ano
28. (OBM)
A figura ao lado mostra três dados iguais. O número da face que é a
base inferior da coluna de dados:
a) é 1.
b) é 2.
c) é 4.
d) é 6.
e) pode ser 1 ou 4.
29. (Epcar) Um aluno da epcar, indagado sobre o número de exercício que havia resolvido naquele dia respondeu:
"Não sei, mas contando de 2 em 2 sobra 1, contando de 3 em 3 sobra 1; contando de 5 em 5 sobra 1, mas
contando de 7 em 7 não sobra nenhum. O total de exercícios não chega a uma centena". Então a soma de todos
os algarismos do número de exercícios resolvidos é igual a:
a) 6
b) 7
c) 8
d) 9
e)10
30. (EPCAR 2012) Em um prédio de 90 andares, numerados de 1 a 90, sem contar o térreo, existem 4 elevadores
que são programados para atender apenas determinados andares. Assim, o elevador
O para nos andares múltiplos de 11
S para nos andares múltiplos de 7
C para nos andares múltiplos de 5
T para em todos os andares.
Todos estes elevadores partem do andar térreo e funcionam perfeitamente de acordo com sua programação.
Analise as afirmativas abaixo, classificando cada uma em V (verdadeira) ou F (falsa)
( ) No último andar para apenas 1 elevador.
( ) Não há neste prédio um andar em que parem todos elevadores, com exceção do próprio térreo.
( ) Existem, neste prédio, 4 andares em que param 3 elevadores com exceção do próprio térreo.
Tem-se a sequência correta em
(A)F,F,V
(B)V,F,V
(C)F,V,F
(D)F,V,V
31. Dê o resultado mais simples da expressão a seguir:
[(
17
12 −
5
4)
2
×
72
10 − (
21
15
−
6
5
) ÷ 3] ÷
1
3
[(
5
2 −
8
5
) ÷ (
3
4 ×
5
3 −
1
2)
2
] ÷
12
5
a) 0
b) 1
c) 2
d) 3
32. A soma do dobro de 3/5 com o dobro de 2/5 é:
a) 1

7. Winter Break - 2016 Homework – Trabalho de Férias 2016 – 6º ano
b) 2
c) 1/2
d) 8/5
33. O inverso da potência (1
3
4
)
2
é:
a) 25/16
b) 49/16
c) 16/49
d) 16/25
34. Se a=3/4; b=1/2; c=2/3, então:
a) a < b
b) a > b + c
c) c > b
d) a . b = c
35. Se a= 5/6; b=1/3 e c=1/2, então:
a) a / b = c
b) a = b + c
c) c = b / c
d) a = b . c
36. (CMRJ) Um aluno do Colégio Militar do Rio de Janeiro escreveu a soma ao lado com a intenção de externar o
carinho por seu colégio. Sabendo que CMRJ representa o ano em que o aluno ingressou no colégio; que cada
letra é um dos algarismos 1, 2,3,4,5,6,7,8 ou 9 e que letras diferentes representam algarismos diferentes, o
valor da soma A + M + O + R é
a) 20
b) 21
c) 23
d) 25
e) 26
37. (CMRJ) Uma das turmas de 9º ano do CMRJ tem 31 alunos. O quociente entre a soma das idades e o número
de alunos é 14. Sabendo-se que, em determinado dia, no qual ninguém havia faltado, quando o professor BV
entrou para iniciar a aula, o chefe de turma perguntou a idade do professor e refez os cálculos, considerando-a
também, encontrando exatamente 15,5. Qual a idade do professor BV?
a) 26 anos.
b) 30 anos.
c) 44 anos.
d) 62 anos.
e) 82 anos.
38. (CMRJ) No dia 16 de outubro, haverá uma distribuição de suco durante a prova de seleção do CMRJ. O militar
responsável pela distribuição possui 10 jarras do tipo B e sabe que cada jarra B corresponde a 7 da jarra A. Sabe-
se ainda que são necessários 12 copos do tipo II, para encher a jarra A e 15 copos 3 do tipo I, para encher a
mesma jarra. Utilizando as 10 jarras do tipo B será possível servir:
C
+ C
M
M
R
R
J
J
A M O R

8. Winter Break - 2016 Homework – Trabalho de Férias 2016 – 6º ano
a) 28 copos do tipo I.
b) 35 copos do tipo I.
c) 120 copos do tipo II.
d) 150 copos do tipo I.
e) 350 copos do tipo I.
39. (CMRJ) A produção bienal de motocicletas no Brasil está sendo exibida no gráfico abaixo. Em qual biênio
houve o maior aumento percentual da produção?
a) 1999 – 2000
b) 2001 – 2002
c) 2003 – 2004
d) 2005 – 2006
e) 2007 – 2008
40. (CMRJ) Uma excelente dica para a resolução de uma prova é dividir o tempo previsto. Em uma prova com 20
questões e 3 horas de duração, se você reservar 10 minutos para o preenchimento do cartão resposta, o tempo
gasto para a resolução de cada questão será, em média, de:
a) 9 minutos.
b) 8 minutos e 50 segundos.
c) 8 minutos e 30 segundos.
d) 8 minutos e 20 segundos.
e) 8 minutos.