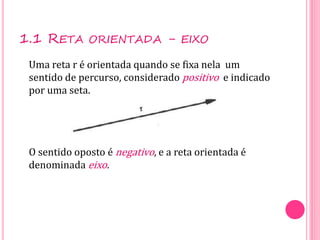
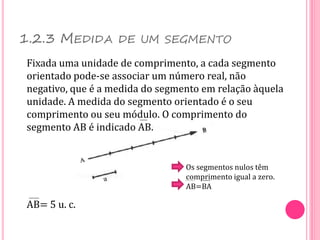
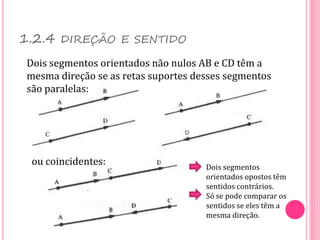
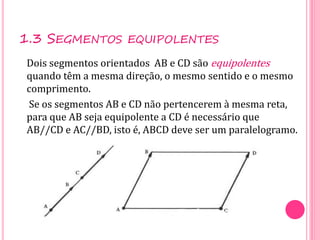
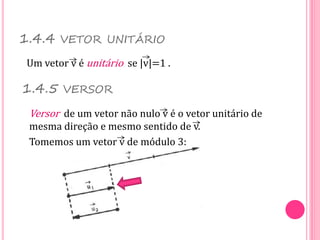
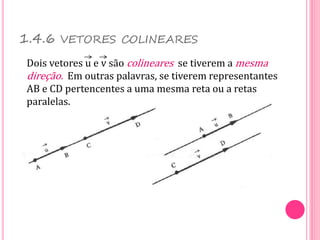
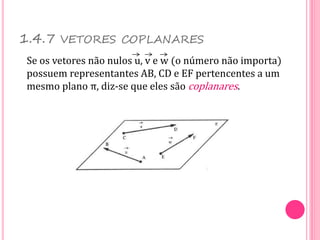
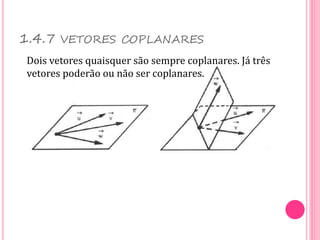
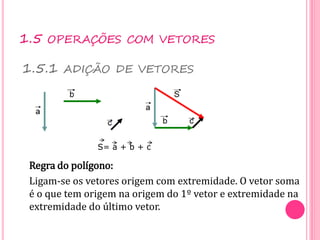
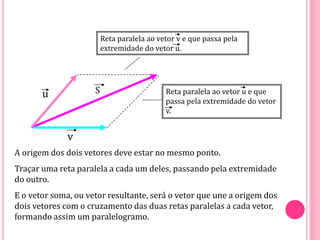
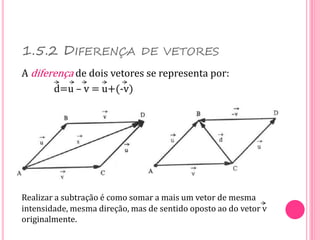
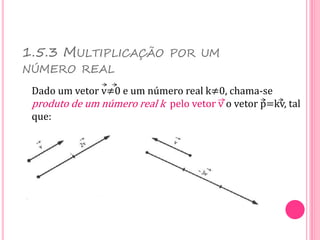
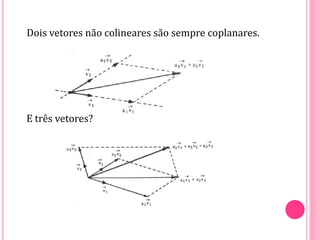
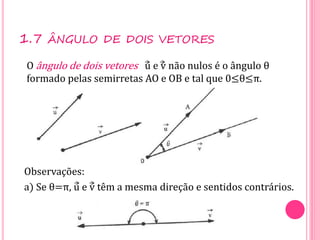
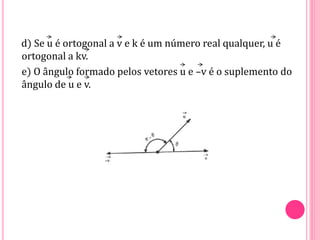
Vetores são grandezas que necessitam de módulo, direção e sentido para serem representadas. Um vetor é determinado por um segmento orientado ou por um conjunto de segmentos equipolentes. As operações com vetores incluem adição, subtração e multiplicação por escalares.