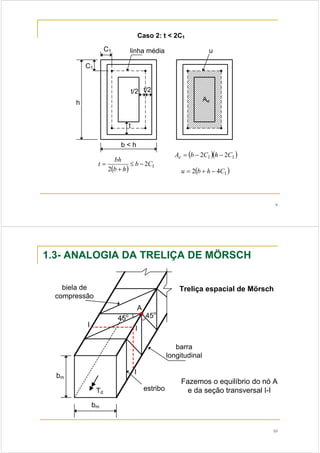
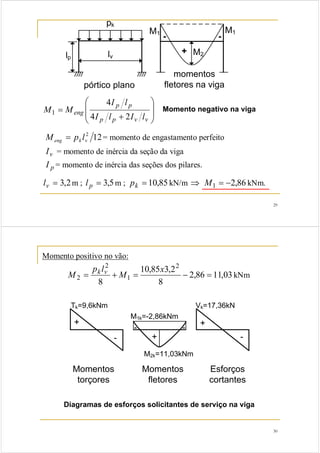
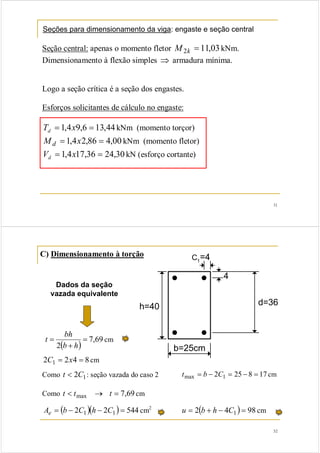
1. O documento discute dimensionamento à torção em vigas de concreto armado, apresentando modelos de treliça, critérios de projeto e exemplos de cálculo. 2. A analogia da treliça de Mörsch é usada para dimensionar a armadura necessária para resistir à torção, considerando estribos verticais, barras longitudinais e bielas de compressão inclinadas a 45°. 3. Os critérios da NBR-6118 para projeto de vigas submetidas à torção incluem verificação das biel

1. 1
Volume 4 – Capítulo 1
DIMENSIONAMENTO À
TORÇÃO
2
1.1- INTRODUÇÃO
Torção de Saint' Venant: não há nenhuma restrição ao
empenamento; só surgem tensões tangenciais.
Torção com empenamento impedido: surgem tensões normais
de tração e de compressão ao longo da barra, além das tensões
tangenciais.
• Algumas formas de seção, como a circular, por exemplo,
não tendem a empenar, de modo que as tensões normais serão
sempre nulas.
h
h
σx
x
T
Dissipação das tensões normais nas
proximidades de um engaste
No caso do
concreto armado,
as tensões
normais são
dissipadas pela
fissuração.

2. 3
Torção de compatibilidade: surge em consequência do
impedimento à deformação (em vigas de borda, por exemplo).
laje
X
momentos
fletores na laje
no estádio I
viga de borda
X
torção na viga
No estádio I, surge o momento de engastamento X da laje, o qual
é um momento torçor por unidade de comprimento para a viga.
Após a fissuração, esse momento torçor diminui muito e não
necessita ser considerado no dimensionamento da viga.
4
Torção de equilíbrio: os momentos torçores são necessários para
satisfazer as condições de equilíbrio.
A A
A-A
momentos fletores
X
-
na marquise
X
T
T
torção na viga

3. 5
1.2- TORÇÃO EM VIGAS DE CONCRETO
ARMADO
• O dimensionamento à torção das estruturas de concreto
armado é feito com base no modelo de treliça de Mörsch. A
treliça é espacial, formada por barras longitudinais, estribos
verticais e bielas de compressão.
• De acordo com a NBR-6118, pode-se escolher uma
inclinação arbitrária para as bielas de compressão, no intervalo
30o ≤θ ≤ 45o .
• Entretanto, na combinação da torção com o esforço cortante,
os ângulos de inclinação das bielas de concreto devem ser
coincidentes para os dois esforços. Assim, empregando-se o
modelo para esforço cortante apresentado no capítulo 6 do
Volume 1, deve-se considerar θ = 45o para o dimensionamento à
torção.
6
• Os ensaios mostram que, após o surgimento das fissuras de
torção, somente uma pequena casca de concreto, junto à face
externa da seção transversal da barra, colabora na resistência à
torção: a resistência à torção de uma seção cheia é equivalente à
resistência de uma seção vazada com as mesmas armaduras.
• O dimensionamento à torção de uma seção cheia é feito para
uma seção vazada equivalente.
t
t linha média
C1
Seção vazada equivalente para uma
seção poligonal convexa maciça
CEB/90: A seção vazada
possui o mesmo contorno
externo da seção maciça e
uma parede de espessura t.

4. 7
t = A (Espessura da parede da seção vazada equivalente)
μ
A= área da seção cheia
μ = perímetro da seção cheia.
Nos casos em que a seção real já é vazada, deve-se considerar o
menor dos seguintes valores para a espessura da parede:
• a espessura real da parede da seção vazada;
• a espessura equivalente calculada supondo uma seção cheia
de mesmo contorno externo da seção vazada.
8
t bh
(b +
h)
=
2
Ae = (b −t)(h −t)
u = 2(b + h − 2t)
Critérios da NBR-6118:

5. 9
Ae = (b − 2C1 )(h − 2C1 )
t bh ≤ −
( ) ( ) u = 2 b + h − 4C1 2 1
2
b C
b +
h
=
10
1.3- ANALOGIA DA TRELIÇA DE MÖRSCH
Treliça espacial de Mörsch
bm
bm
A
Td estribo
barra
longitudinal
biela de
compressão
45o 45o
I I
I
Fazemos o equilíbrio do nó A
e da seção transversal I-I

6. Fte = Fc ⇒F = F (1.3.1)
Fts = Fc ⇒F = F (1.3.2)
11
Equilíbrio do nó A:
Fte
F Fc c
Fte
Fts
Fts
45o
45o
A
Forças em um
nó da treliça
Força de tração nos estribos:
o
cos 45 te c 2
Força nas barras longitudinais:
o
cos 45 ts c 2
12
Equilíbrio da seção transversal:
Fc/ 2
bm Projeção das forças de
Fc/ 2
Fc/ 2 bm
Fc/ 2
compressão na seção
transversal
Equilíbrio da seção transversal:
2 c
2
d m
F
T = b (1.3.3)
Força de compressão na biela de concreto:
T
d
F = (1.3.4)
c b
m 2

7. 13
Substituindo (1.3.4) nas equações (1.3.1) e (1.3.2):
d
= = (1.3.5)
te ts b
m
T
F F
2
Dimensionamento dos estribos:
As1= área da seção transversal de um estribo.
s = espaçamento dos estribos ao longo do eixo da peça.
A área total de aço em um comprimento bm é
A = (1.3.6)
s1
b
m
s A
s
Força de tração resistente:
F = A f = 1 (1.3.7)
m yd
A
s
ter s yd b f
s
Iguais para garantir equilíbrio
14
Fazendo Fter = Fte , chega-se a
T
A
s d
1 = , cm2/cm (1.3.8)
A f
e yd
s
2
onde 2m
Ae = b é a área limitada pela linha média da parede
fictícia.
T
100 = d
, cm2/m (1.3.9)
sw A f
e yd
A
2
Área de estribos por metro
de comprimento da viga

8. 15
Observações:
• No caso da torção, só se pode contar com um ramo dos
estribos, pois todos os ramos estão submetidos à força de tração
Fte , inclusive aqueles situados nas faces superior e inferior da
viga.
• Desse modo, os estribos para torção devem ser fechados,
obrigatoriamente.
• Antes de empregar as tabelas para estribos de 2 ramos
constantes no Apêndice 3 do Volume 2, deve-se multiplicar a área
Asw por 2.
16
Dimensionamento da armadura longitudinal:
Fts
bm
bm
modelo
Asl
disposição real
Modelo e disposição
real das barras
longitudinais na seção
d
= = (equação (1.3.5))
te ts b
m
T
F F
2
Fts = força de tração solicitante concentrada em cada quina da
seção
Força fts por unidade de comprimento da linha média da parede
F
fictícia:
d
= = (1.3.10)
ts A
e
ts
m
T
b
f
2

9. 17
Força de tração resistente por unidade de comprimento da linha
A f
média:
f sl yd
tsr = (1.3.11)
u
onde Asl é a área da seção das barras longitudinais distribuídas ao
longo da linha média da parede fictícia e u é o perímetro da linha
média da parede.
Igualando (1.3.11) a (1.3.10), resulta
T u
d
= , cm2 (1.3.12)
sl A f
e yd
A
2
Área total da armadura longitudinal,
distribuída ao longo da linha média
18
Verificação das bielas de compressão:
bm
45o
ho
t
Fc
seção vazada
vista lateral
Solicitação na
biela inclinada
A força Fc atua em uma área Ac = tho , onde t é a espessura da
parede fictícia e ho é a dimensão normal à força, dada por
o
ho = bm sen 45 ⇒h o = b m 2
(1.3.13)
T
d
F = (1.3.4)
c b
m 2
Visto anteriormente
Fazendo σ c = Fc Ac , resulta:
T
e
d
σ c = (1.3.14)
A t

10. 19
Considerando a distribuição das tensões tangenciais na seção
transversal vazada, pode-se demonstrar (ver cap.1, Volume 4) que
σ c = 2τ td , onde
T
d
e
τ = T e n s ã o (1.3.22)
A t
td 2
convencional de
cisalhamento
Segundo a NBR-6118, deve-se limitar σ c ≤ 0,50α v fcd , para não
haver esmagamento das bielas.
Fazendo isto, resulta
τ td ≤τ tu (1.3.24)
onde τ tu = 0,25α v fcd (1.3.25)
sendo α v = 1− fck 250, com fck em MPa.
20
1.4- CRITÉRIO DE PROJETO DA NBR-6118
Verificação da segurança das bielas:
T τ = ≤τ
tu
d
td A t
e
2
; τ tu = 0,25α v fcd ;
α v = 1− fck 250 com fck em MPa
Nos casos correntes, onde há torção com flexão, deve-se garantir
τ
que + wd
≤ 1
wu
τ
td
tu
τ
τ
onde τ wd e τ wu são as tensões tangenciais obtidas no
dimensionamento ao esforço cortante.

11. 21
Estribos verticais para torção:
T
100 = d
, cm2/m
sw A f
e yd
A
2
Armadura longitudinal:
T u
d
= , cm2
sl A f
e yd
A
2
Para o cálculo das armaduras, deve-se limitar a tensão de
escoamento do aço em 435 MPa.
Observações:
1) Os estribos para torção devem ser fechados e com
extremidades ancoradas por meio de ganchos em ângulo de 45o. O
diâmetro da barra do estribo deve ser maior ou igual a 5 mm e não
deve exceder 1/10 da largura da alma da viga.
22
2) As armaduras obtidas nos dimensionamentos à torção e à
flexão são superpostas. Na soma das seções necessárias dos
estribos, deve-se lembrar que para a torção só se pode contar com
um ramo dos mesmos.
Área total de estribos: Asw,tot = Asw,V + 2Asw,T
Asw,V = área dos estribos para o esforço cortante
Asw,T = área de estribos para torção.
3) A área total dos estribos, Asw,tot , deve respeitar a área mínima,
Asw,min = ρ w,min100bw , cm2/m, onde bw é a largura média da
seção da peça.
ctm
yk
f
ρ ,min = 0,2
w f

12. 23
Tabela 1.4.1 - Valores de ρ w,min (%) para o aço CA-50
fck (MPa) 20 25 30 35 40 45 50
ρ w,min 0,09 0,10 0,12 0,13 0,14 0,15 0,16
fck (MPa) 55 60 70 80 90
ρ w,min 0,17 0,17 0,18 0,19 0,20
4) O espaçamento máximo dos estribos é dado por
smax = 0,6d ≤ 30 cm, se τ td τ tu +τ wd τ wu ≤ 0,67 ;
smax = 0,3d ≤ 20 cm, se τ td τ tu +τ wd τ wu > 0,67 ;
onde d é a altura útil da seção da viga.
5) A área mínima da armadura longitudinal, Asl,min , é dada por
Asl min ub
ρ
2
w min
= ,
, w
, cm2, onde u é o perímetro da linha média da
parede da seção vazada equivalente e ρw,min é dado na tabela.
24
6) Em cada canto da armadura transversal, devem-se colocar
barras longitudinais de bitola pelo menos igual à da armadura
transversal e não inferior a 10.
7) Em seções retangulares com dimensões não superiores a 40cm,
a armadura longitudinal para torção pode ser concentrada nos
cantos. Em seções maiores, a armadura longitudinal deve ser
distribuída ao longo do perímetro da seção, para limitar a abertura
das fissuras. Recomenda-se que o espaçamento dessas barras não
seja superior a 20 cm. Em qualquer caso, as barras longitudinais
devem ser distribuídas de forma a manter constante a relação
Asl u .

13. 25
1.5- EXEMPLO DE DIMENSIONAMENTO
lv=3,2m
0,25 1,5m
A
25
40
parede: h=1m,
10cm
6
e=15cm
A-A
marquise
A
P1-25x25
P2-25x25
Viga suportando uma marquise
26
f
= ck =
f MPa
Concreto: fck = 20MPa; 14,3
1,4
cd
αv =1− fck 250 =1− 20 250 = 0,92
τ wu = 0,27α v fcd ⇒τ wu = 3,5MPa
τ tu = 0,25α v fcd ⇒τ tu = 3,2MPa
A) Cálculo da marquise
Cargas de serviço na marquise:
- peso próprio: 2
25 ⎛ 0,10 +
0,06 ⎞
2
⎟⎠
= ⎜⎝
kN/m2
- revestimento: 0,8 kN/m2
- carga acidental: 0,5 kN/m2
- carga acidental na extremidade do balanço: 1 kN/m

14. 27
1 kN/m
3,3 kN/m2
lm=1,63 m
Rk
Xk
Modelo de cálculo da marquise
Rk = 6,4 kN/m
X k = 6 kNm/m
B) Esforços na viga
Momento torçor por unidade de comprimento X k = 6 kNm/m.
T 9,6
kNm (momento torçor)
X k l v
6 x
3,2
k T = = ⇒ k =
2
2
k V V p l x kN
28
Cargas verticais aplicadas na viga:
- ação da marquise: Rk = 6,4 kN/m
- peso próprio: 25x0,25x0,4 = 2,5 kN/m
- parede de tijolo furado: 13x0,15x1=1,95 kN/m
Carga total de serviço: pk = 10,85 kN/m.
Esforço cortante de serviço:
17,36
10,85 3,2
k v
= = ⇒ k =
2
2

15. 29
⎞
⎟ ⎟
1 Momento negativo na viga
⎠
⎛
⎜ ⎜
I l
4
eng I l I l
⎝
p p
+
=
p p v v
M M
4 2
2 12
eng k v M = p l = momento de engastamento perfeito
Iv = momento de inércia da seção da viga
I p = momento de inércia das seções dos pilares.
lv = 3,2m ; l p = 3,5m ; pk = 10,85 kN/m ⇒ M1 = −2,86 kNm.
30
Momento positivo no vão:
2,86 11,03
10,85 3,2
8
p l
8
2
1
2
2 = + = − = M x
M k v kNm
Diagramas de esforços solicitantes de serviço na viga

16. 31
Seções para dimensionamento da viga: engaste e seção central
Seção central: apenas o momento fletor M2k = 11,03 kNm.
Dimensionamento à flexão simples ⇒ armadura mínima.
Logo a seção crítica é a seção dos engastes.
Esforços solicitantes de cálculo no engaste:
T = 1,4x9,6 = 13,44 d kNm (momento torçor)
Md = 1,4x2,86 = 4,00 kNm (momento fletor)
V = 1,4x17,36 = 24,30 d kN (esforço cortante)
C1=4
h=40 d=36
t bh cm
2C1 = 2x4 = 8 cm
Como t < 2C1: seção vazada do caso 2 tmax = b − 2C1 = 25 − 8 = 17 cm
Como t < tmax → t = 7,69 cm
Ae = (b − 2C1 )(h − 2C1 ) = 544 cm2 u = 2(b + h − 4C1 ) = 98 cm
32
C) Dimensionamento à torção
b=25cm
4
Dados da seção
vazada equivalente
2
( ) =
7,69
+
=
b h

17. 33
Verificação das tensões no concreto:
T τ d
1344
τ 0,161
kN/cm2 (τ td = 1,61MPa)
= = ⇒ td =
td A t x x
2 544 7,69
2
e
τ V τ 0,027
kN/cm2 (τ wd = 0,27MPa)
= = 24,3 ⇒ = wd
wd b d x
25 36
d
w
τ
wd
+ = 0,58 < 1
wu
τ
td
tu
τ
τ
OK!
34
Cálculo das armaduras ( f yd = 43,48 kN/cm2):
A
T
A f
x
100
2
sw A
= = ⇒ sw T =
x x
d
e yd
100 1344
2 544 43 48
2 84
,
, , cm2/m
A T d
u 1344 x
98
2,78
cm2
sl A
= = ⇒ sl =
2 544 43,48
2
e yd
x x
A f
Armadura longitudinal mínima:
ρw,min = 0,09% é dado na tabela
Asl,min = (ρw,min 2)ubw = 1,10cm2
Logo, prevalece o valor calculado Asl = 2,78 cm2.

18. 35
D) Dimensionamento à flexão
Para o esforço cortante Vd = 24,30 kN, resulta Asw,V = 0,
pois τ d =1,11(τ wd −τ c ) = 0 .
Para o momento fletor Md = 4,00kNm, resulta a armadura mínima
As,min minbh x x
015
,
100
25 40 1 5cm2 ⇒ As = 15 , cm2
= ρ = = ,
E) Superposição das armaduras
Área total dos estribos:
Asw,tot = Asw,V + 2Asw,T = 0 + 2x2,84 = 5,68 cm2/m
Área mínima de estribos:
Asw,min = ρ w,min100bw = 2,25 cm2/m ⇒ Asw,tot = 5,68 cm2/m.
36
Como resultou τ td τ tu +τ wd τ wu ≤ 0,67 :
d cm
0,6 21,6
⎩ ⎨ ⎧
max smax
s ⇒ =
cm
=
= 21
cm
30
Tabela A3.3 (Apêndice 3 do Volume 2):
Para Asw,tot = 5,68 cm2/m, obtém-se a solução φ 6,3c.10 .
OK!
As Asl/2
2φ12,5+1φ8
=
Superposição das armaduras longitudinais
Engastar as
armaduras
longitudinais nos
pilares
As=1,5cm2
+
Asl/2=1,39cm2
2φ12,5+1φ8(2,95cm2)
para
Md
para
Td