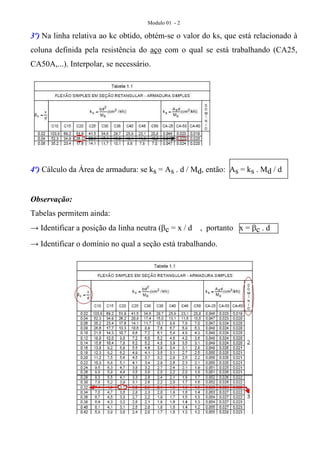
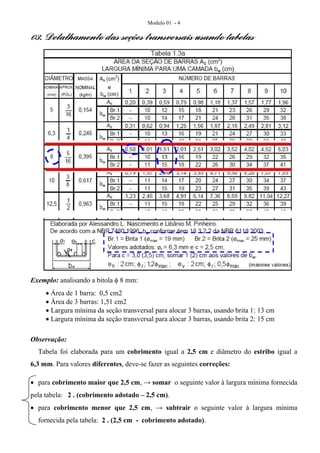
1) O documento apresenta os procedimentos para dimensionamento de seções retangulares submetidas à flexão simples, utilizando tabelas para determinar a área de armadura necessária. 2) São mostrados exemplos de dimensionamento para armadura simples e dupla, além de detalhamento das seções transversais considerando espaçamentos mínimos entre barras. 3) São apresentados exercícios para aplicação dos procedimentos ensinados.

1. Modulo 01 - 1
Módulo 01 - Revisão
01. Dimensionamento, mediante o uso de tabelas, de uma seção
retangular submetida à flexão simples (armadura simples)
• Momento Fletor (Md) – gera tração na armadura e compressão no concreto
• profundidade x: define a região
comprimida, usando o diagrama de
tensões parábola-retângulo
• profundidade y (= 0,8 x): define a
região comprimida, usando o diagrama
de tensões retangular (simplificação)
Tabela 1.1 do Prof. Libânio Miranda Pinheiro:
1º) Calcular o valor de uma constante: kc = ( b d2 ) / Md
2º) Na coluna definida pela resistência do concreto (C-10, C-15, C-20,...),
identificar o valor do kc.

2. Modulo 01 - 2
3º) Na linha relativa ao kc obtido, obtém-se o valor do ks, que está relacionado à
coluna definida pela resistência do aço com o qual se está trabalhando (CA25,
CA50A,...). Interpolar, se necessário.
4º) Cálculo da Área de armadura: se ks = As . d / Md, então: As = ks . Md / d
Observação:
Tabelas permitem ainda:
→ Identificar a posição da linha neutra (βc = x / d , portanto x = βc . d
→ Identificar o domínio no qual a seção está trabalhando.

3. Modulo 01 - 3
02. Dimensionamento, mediante o uso de tabelas, de uma seção
retangular submetida à flexão simples (armadura dupla)
Momento Fletor (Md) – é absorvido por duas parcelas: Md = M1 + M2
M1: concreto comprimido + armadura tracionada As1, correspondente ao máximo momento que a
seção agüenta no limite entre os domínios 3 e 4.
M2: armadura comprimida (As´) e armadura tracionada (As2), correspondente ao momento que a
parcela anterior não consegue absorver.
Tabela 1.2 do Prof. Libânio Miranda Pinheiro:
d: distância da borda comprimida ao c.g. da
armadura tracionada As
d´: distância da borda comprimida ao c.g. da
armadura comprimida As´
(geralmente adota-se d´ = 3 cm)
Roteiro:
1º) Determinar o valor do kc limite entre os domínios 3 e 4 ( kc,lim ): com a tabela 1.1 e com o tipo de
aço, determinamos o valor do ks,lim. Na linha correspondente a esse ks,lime na coluna da resistência
do concreto, obtemos o kc,lim .
2º) Calcular os valores de M1 e As1.
3º) Determinar o valor de ks2 (tabelado) e de M2 (= Md – M1 ), para depois calcular o valor de As2
4º) Determinar o valor de ks´ (tabelado) e calcular o valor de As´
5º) Determinar o valor da armadura tracionada As ( = As1 + As2 ) e da armadura comprimida (As´)

4. Modulo 01 - 4
03. Detalhamento das seções transversais usando tabelas
Exemplo: analisando a bitola φ 8 mm:
• Área de 1 barra: 0,5 cm2
• Área de 3 barras: 1,51 cm2
• Largura mínima da seção transversal para alocar 3 barras, usando brita 1: 13 cm
• Largura mínima da seção transversal para alocar 3 barras, usando brita 2: 15 cm
Observação:
Tabela foi elaborada para um cobrimento igual a 2,5 cm e diâmetro do estribo igual a
6,3 mm. Para valores diferentes, deve-se fazer as seguintes correções:
• para cobrimento maior que 2,5 cm, → somar o seguinte valor à largura mínima fornecida
pela tabela: 2 . (cobrimento adotado – 2,5 cm).
• para cobrimento menor que 2,5 cm, → subtrair o seguinte valor à largura mínima
fornecida pela tabela: 2 . (2,5 cm - cobrimento adotado).

5. Modulo 01 - 5
• para φestribo (em centímetros) maior que 0,63 cm → somar o seguinte valor à largura
mínima fornecida pela tabela: 2 . ( φestribo – 0,63 cm).
• para φestribo (em centímetros) menor que 0,63 cm, → subtrair o seguinte valor à largura
mínima fornecida pela tabela: 2 . ( 0,63 cm - φestribo ).
Relembrando as recomendações da norma:
eh: distancia livre entre barras, na direção horizontal
⎧
⎪⎩
⎪⎨
20 mm
φ
e ≥ φ
l
max,agregado
h
1,2
ev: distancia livre entre barras, na direção vertical
⎧
⎪⎩
⎪⎨
20 mm
φ
e ≥ φ
l
max,agregado
v
0,5
Verificação da abertura para passagem do vibrador: p/ cada posição de vibração, sugere-se:
a) considerar um raio de ação de 30 cm e a possibilidade do vibrador penetrar até a primeira
camada
b) deixar uma abertura para a posição da vibração com largura no mínimo igual ou superior ao
diâmetro do vibrador mais 2 cm
(ver figura adaptada do livro COMENTÁRIOS DA NB-1, mostrada a seguir).

6. Modulo 01 - 6
Importante 01)
Pode-se adotar uma área de armadura efetiva menor que a calculada desde que:
0,95
A
s,calculada
A
s,efetiva ≥
Importante 02)
Após o detalhamento, deve-se fazer a seguinte verificação:
real ≥ ⇒
Se 0,95 então OK!
d
d
usado no cálculo
real < ⇒
Se 0,95 redimensionar!
d
d
usado no cálculo
onde:
Σ
=
A . d
Σ
si i
si
real A
d
Lista de Exercícios
01) Dimensionar a área de armadura de flexão para as seções transversais mostradas nas figuras a seguir. Adotar
armadura dupla, quando necessário.
a) Base (b) de 30 cm, Altura (h) de 54 cm, Concreto
C20, Aço CA50, Momento fletor característico (Mk)
igual a 194 kN.m.
b) Base (b) de 12 cm, Altura (h) de 50 cm, Concreto
C25, Aço CA50, Momento fletor característico (Mk)
igual a 150 kN.m.
02) Considerando-se o item b) do exercício 1), pede-se determinar a altura h da seção transversal, para que não
seja necessária a utilização de armadura dupla, e também o valor da nova área de armadura simples a ser
utilizada nessa seção.