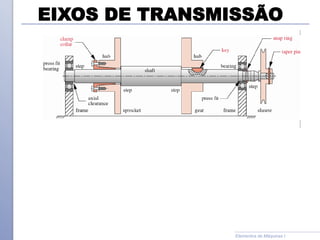
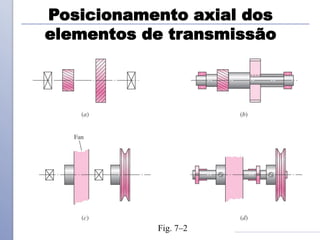
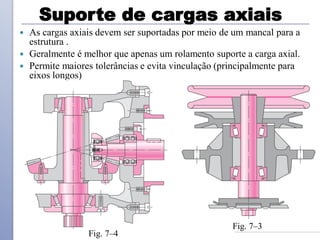
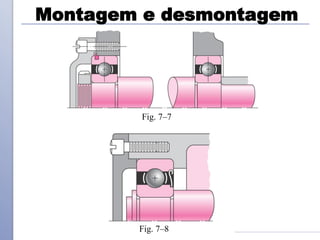
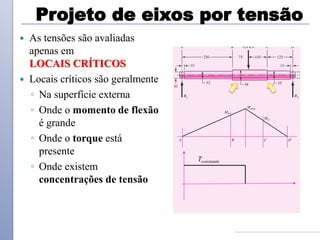
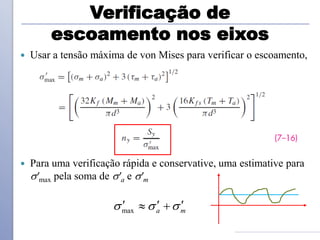
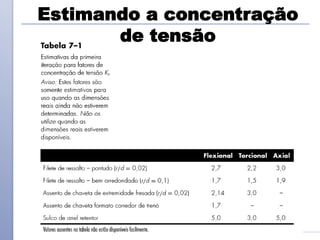
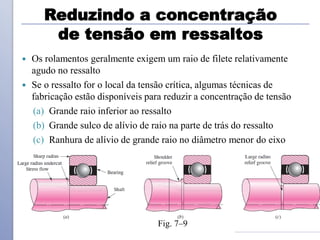
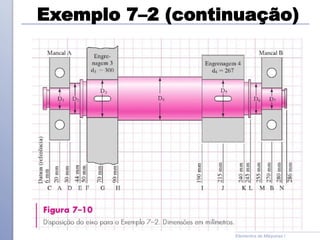
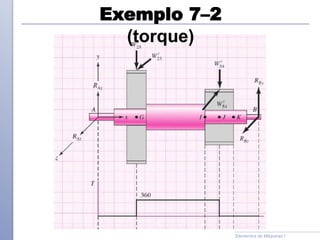
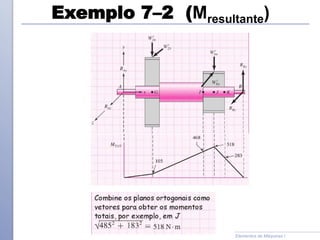
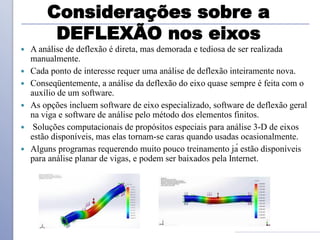
O documento descreve os critérios e métodos de projeto de eixos de transmissão. Discute como posicionar os componentes ao longo do eixo e como projetar o eixo para resistir às tensões causadas por torção e flexão. Também aborda como estimar concentrações de tensão e dimensionar o eixo para limites de deflexão.