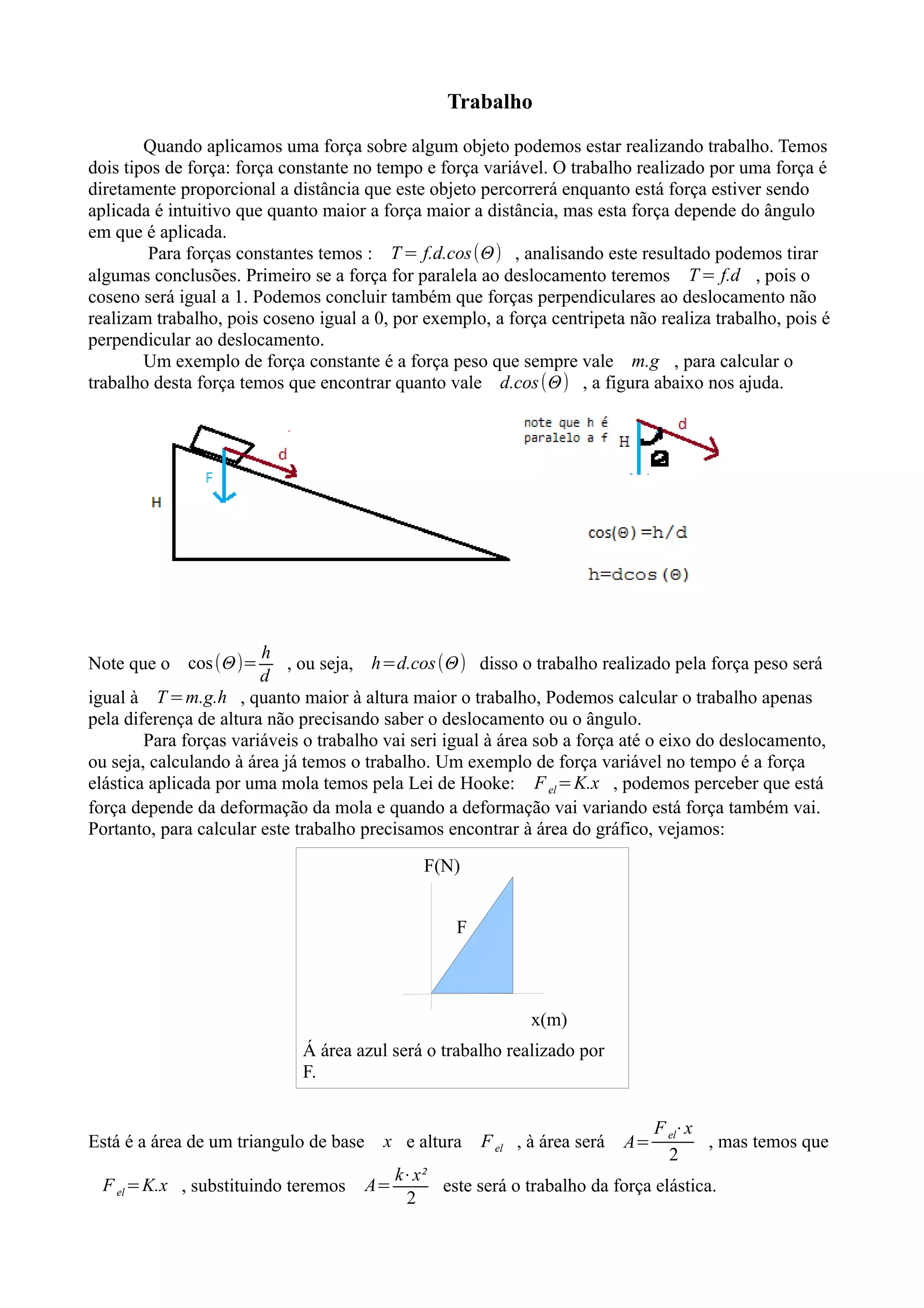
1) Existem dois tipos de força: constante e variável no tempo. 2) Para forças constantes, o trabalho é dado por T=f.d.cos(Θ). Se a força for paralela ao deslocamento, o trabalho é máximo. 3) Para forças variáveis, o trabalho é dado pela área sob a curva da força em função do deslocamento.

1. Trabalho
Quando aplicamos uma força sobre algum objeto podemos estar realizando trabalho. Temos
dois tipos de força: força constante no tempo e força variável. O trabalho realizado por uma força é
diretamente proporcional a distância que este objeto percorrerá enquanto está força estiver sendo
aplicada é intuitivo que quanto maior a força maior a distância, mas esta força depende do ângulo
em que é aplicada.
Para forças constantes temos : T = f.d.cos(Θ) , analisando este resultado podemos tirar
algumas conclusões. Primeiro se a força for paralela ao deslocamento teremos T = f.d , pois o
coseno será igual a 1. Podemos concluir também que forças perpendiculares ao deslocamento não
realizam trabalho, pois coseno igual a 0, por exemplo, a força centripeta não realiza trabalho, pois é
perpendicular ao deslocamento.
Um exemplo de força constante é a força peso que sempre vale m.g , para calcular o
trabalho desta força temos que encontrar quanto vale d.cos (Θ) , a figura abaixo nos ajuda.
h
Note que o cos (Θ)= , ou seja, h=d.cos (Θ) disso o trabalho realizado pela força peso será
d
igual à T =m.g.h , quanto maior à altura maior o trabalho, Podemos calcular o trabalho apenas
pela diferença de altura não precisando saber o deslocamento ou o ângulo.
Para forças variáveis o trabalho vai seri igual à área sob a força até o eixo do deslocamento,
ou seja, calculando à área já temos o trabalho. Um exemplo de força variável no tempo é a força
elástica aplicada por uma mola temos pela Lei de Hooke: F el =K.x , podemos perceber que está
força depende da deformação da mola e quando a deformação vai variando está força também vai.
Portanto, para calcular este trabalho precisamos encontrar à área do gráfico, vejamos:
F(N)
F
T
x(m)
Á área azul será o trabalho realizado por
F.
F el⋅x
Está é a área de um triangulo de base x e altura F el , à área será A= , mas temos que
2
k⋅x²
F el =K.x , substituindo teremos A= este será o trabalho da força elástica.
2

2. Portanto para calcular o trabalho de uma força constante utilazermos T = f.d.cos(Θ) , por
exemplo, o trabalho da força peso será T =m.g.h . Para calcular o trabalho de uma força váriavel
F ⋅x
temos que calcular à área do gráfico, por exemplo, na força elástica teremos A= el . Não
2
podemos esquecer que temos algumas forças que não realizam trabalho, por exemplo, a força
centripeta, pois é perpendicular ao deslocamento.