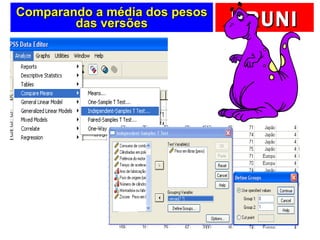
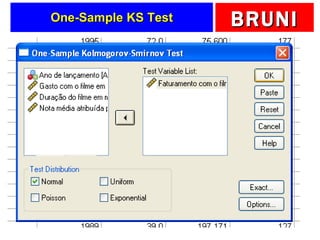
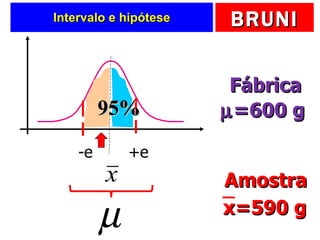
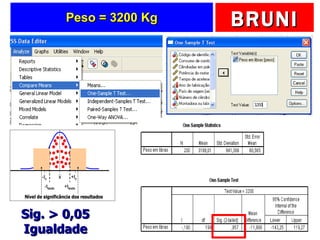
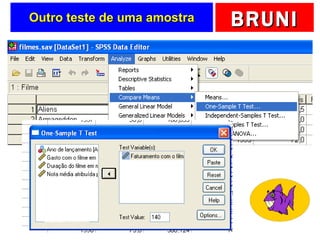
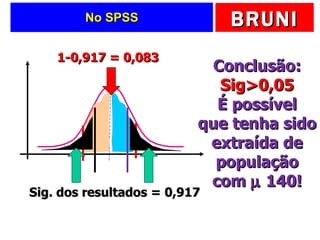
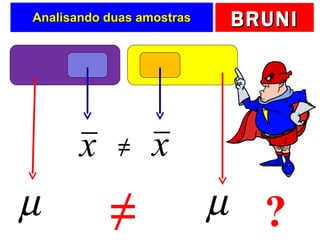
1) O documento discute testes estatísticos paramétricos e não paramétricos para analisar amostras e comparar com populações. 2) É apresentado um exemplo para testar se a variável faturamento de filmes foi extraída de uma população com média de 140 milhões de dólares. 3) Também é mostrado como testar se as médias de duas amostras (por exemplo, versões de carros) são iguais ou diferentes.

1. Relembrando as ... 6. Aplicando testes paramétricos de hipóteses Vamos confrontar amostra e universo!

2. Para pensar ... Einstein “ A Matemática não mente. Mente quem faz mau uso dela”.

3. Paramétrico por quê? Fazemos suposição sobre a forma de distribuição do parâmetro na população dos dados Média normalmente distribuída Amostras grandes (n >=30) Teorema central do limite Amostras pequenas (n<30) Teste da variável original Teste de forma de Kolmogorov-Smirnov

4. Analisando filmes.sav Teste se a variável Faturamento foi extraída de uma população normalmente distribuída. Use o teste não paramétrico de K-S

5. Nonparametric Tests > 1-S K-S

6. One-Sample KS Test

7. Resultados do SPSS Sig>0,05: Normal Distribuição = Normal

8. Para facilitar em sala de aula Vamos analisar amostras grandes!

9. Uma alegação do fabricante Pesa em média 600 gramas! Duvido! Minha amostra pesou menos!

10. Lendo o livro!

11. Intervalo e hipótese 95% +e -e  =600 g Fábrica x=590 g Amostra

12. Confiança e Significância Aceito igualdade H 0 Rejeito igualdade H 1 Nível de confiança Nível de significância

13. No SPSS Resultado Sig. dos resultados Sig. > 0,05: Igualdade Sig. < 0,05: Desigualdade

14. Analisando filmes.sav Estabeleça hipóteses para teste se a variável Faturamento foi extraída de uma população com média igual a: a) 140 ($ milhões) b) 160 ($ milhões) c) 200 ($ milhões)

15. No planejamento ... Duas hipóteses: a nula (H 0 ) sempre contém uma igualdade e a alternativa (H 1 ) sempre apresenta uma desigualdade 140 ($ milhões) H 0 :  = 140 H 1 :   140 b) 160 ($ milhões) H 0 :  = 160 H 1 :   160 c) 200 ($ milhões) H 0 :  = 200 H 1 :   200

16. Analisando a base de carros Testes de uma amostra

17. Da base carros.sav Pesam em média 3200 Kg! H 0 :  =3200 H 1 :  ≠3200

18. Peso = 3200 Kg Sig. > 0,05 Igualdade

19. Analisando outra base ... Filmes.sav! 140 ($ milhões) H 0 :  = 140 H 1 :   140 b) 160 ($ milhões) H 0 :  = 160 H 1 :   160 c) 200 ($ milhões) H 0 :  = 200 H 1 :   200

20. Outro teste de uma amostra

21. Resultados para 140 Sig>0,05: Igual! 137,97161-140

22. No SPSS Sig. dos resultados = 0,917 1-0,917 = 0,083 Conclusão: Sig>0,05 É possível que tenha sido extraída de população com  140!

23. Outros testes ...  = 160, Sig=0,261: Igual!  = 200, Sig=0,003: Diferente!

24. Analisando a base de carros Testes de duas amostras As médias são iguais?

25. Analisando duas amostras ≠ ≠ ?

26. Teste da diferença! H 0 :  a -  b =d H 1 :  a -  b ≠d d = diferença d = 0 (iguais)

27. Comparando a média dos pesos das versões

28. Output no SPSS Sig<0,05: Diferentes!

29. Para ficar esperto! Resolva os exercícios do capítulo