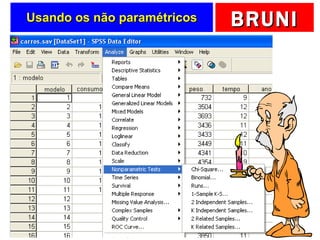
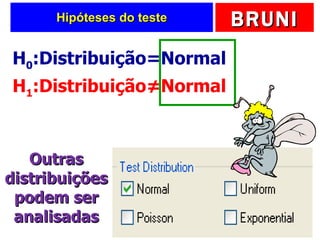
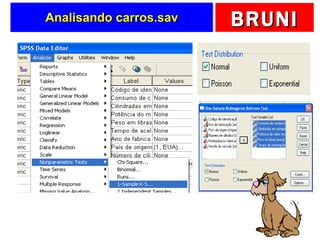
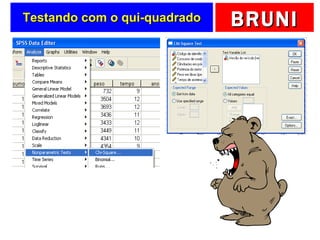
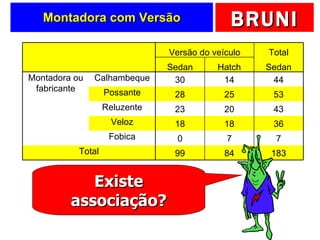
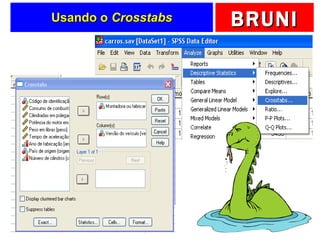
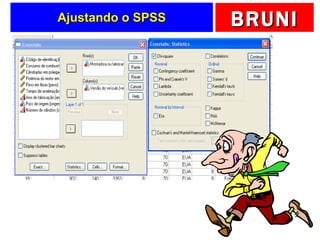
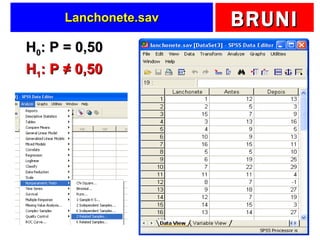
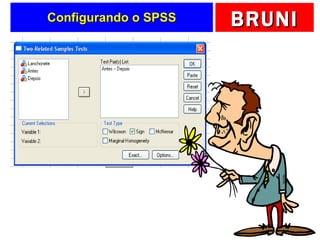
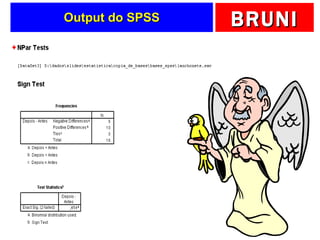
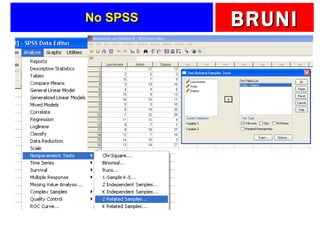
a) O documento descreve vários testes estatísticos não paramétricos para análise de dados, incluindo teste de Kolmogorov-Smirnov, teste do qui-quadrado, teste dos sinais, teste de Wilcoxon e teste de Kruskal-Wallis. b) Fornece detalhes sobre quando cada teste é apropriado dependendo do tipo de dados e objetivo da análise, como testar a forma da distribuição, associação entre variáveis ou comparar médias entre grupos. c) Apresenta exemplos práticos aplicando cada teste

1. Relembrando as ... 7. Usando testes não paramétricos de hipóteses Vamos analisar amostras pequenas!

2. Para pensar ... Einstein “ Imaginação é tudo!”.

3. Tipos de testes a) Teste de Kolmogorov-Smirnov: analisa se os dados da amostra foram extraídos de uma população com uma distribuição peculiar de freqüências, como a distribuição Normal; b) Teste do qui-quadrado: empregado na análise de freqüências, quando uma característica da amostra é analisada; c) Teste do qui-quadrado para independência ou associação: também empregado na análise de freqüências, porém quando duas características da amostra são analisadas; d) Teste dos sinais: empregado no estudo de dados emparelhados, quando um mesmo elemento é submetido a duas medidas; e) Teste de Wilcoxon: também analisa dados emparelhados, permitindo, porém, uma consideração das magnitudes encontradas; f) Teste de Mann-Whitney: analisa se dois grupos originam-se de populações com médias diferentes; g) Teste da mediana: analisa se dois grupos originam-se de populações com medianas diferentes; h) Teste de Kruskal-Wallis: analisa se K (K > 2) grupos originam-se de populações com médias diferentes.

4. O que quer? Analisar a forma da distribuição? Kolmogorov-Smirnov Analisar concentração de freqüência? Qui-quadrado de uma variável Analisar associação de duas variáveis qualitativas? Qui-quadrado de duas variáveis Testar a média de dois grupos? Mann Whitney Testar a mediana de dois grupos? Mediana

5. O que quer? Testar a média de mais de dois grupos? Kruskal Wallys Testar dados emparelhados? Sinais Wilcoxon

6. Usando os não paramétricos

7. Analisando a base de carros Teste de Kolmogorov-Smirnov

8. Já vimos! Teste de forma de Kolmogorov-Smirnov Testa a forma da distribuição na população Eu sou Normal?

9. Hipóteses do teste H 0 :Distribuição=Normal H 1 :Distribuição≠Normal Outras distribuições podem ser analisadas

10. Analisando carros.sav

11. Analisando o output Fundamental em amostras pequenas

12. Analisando a base de carros Teste do qui-quadrado

13. Preste atenção! Uma variável! Análise da concentração de frequências!

14. Com uma amostra H 0 : F 1 = F 2 H 1 : F 1 ≠ F 2 Tabela do Qui-quadrado

15. Testando com o qui-quadrado

16. Output do SPSS

17. Preste atenção! Duas variáveis! Análise da associação!

18. Montadora com Versão Existe associação? Versão do veículo Total Sedan Hatch Sedan Montadora ou fabricante Calhambeque 30 14 44 Possante 28 25 53 Reluzente 23 20 43 Veloz 18 18 36 Fobica 0 7 7 Total 99 84 183

19. Hipóteses do teste H 0 :Variáveis não são associadas H 1 :Variáveis são associadas Verificamos se duas variáveis podem estar associadas!

20. Usando o Crosstabs

21. Ajustando o SPSS

22. Análise da significância

23. Analisando a base de carros Teste dos sinais

24. Definição dos sinais Dados emparelhados Antes versus Depois Sinais “+” (mais) e “–” (menos) no lugar dos dados numéricos originais. H 0 : Antes = Depois H 1 : Antes ≠ Depois

25. Lanchonete.sav H 0 : P = 0,50 H 1 : P ≠ 0,50

26. Configurando o SPSS

27. Output do SPSS

28. Analisando a base de carros Teste de Wilcoxon

29. Conceito Evolução do teste dos sinais, permitindo considerar a magnitude da diferença de cada par. H 0 : Antes = Depois H 1 : Antes ≠ Depois

30. No SPSS

31. Output de Wilcoxon

32. Analisando a base de carros Teste de Mann-Whitney

33. Entendendo o teste Análise sobre o fato de duas amostras independentes terem sido extraídas de populações com médias iguais. H 0 :  a =  b H 1 :  a ≠  b

34. No SPSS

35. Output SPSS

36. Analisando a base de carros Teste da Mediana

37. Entendendo o teste Testa a hipótese de dois grupos independentes terem ou não medianas populacionais iguais, podendo ser aplicado, também, para variáveis ordinais ou intervalares. H 0 :mediana a =mediana b H 0 :mediana a ≠mediana b

38. No SPSS

39. Output do SPSS

40. Analisando a base de carros Teste de Kruskal-Wallis

41. Entendendo o teste Análise do fato de K ( K >2) amostras independentes serem originárias ou não de populações com médias iguais, podendo ser aplicado, também, com variáveis intervalares ou ordinais. H 0 :  a =  b =  c =  H 1 :pelo menos uma média é diferente

42. Configurando o SPSS

43. Output do SPSS