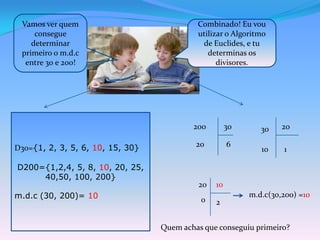
O documento explica como calcular o máximo divisor comum (MDC) entre dois números usando o algoritmo de Euclides. Primeiro, divide-se o maior número pelo menor repetidamente até obter um resto zero, indicando que o último divisor é o MDC. Em seguida, calcula-se o MDC entre 240 e 135, que é igual a 15.

1. O algoritmo de Euclides permite calcular o máximo divisor
comum entre dois números, de um modo rápido e fácil!
Vamos calcular
então, o m.d.c entre
dois números
utilizando este
algoritmo…

3. Vamos determinar o m.d.c entre 240 e 135:
 Em primeiro lugar dividimos 240 por 135
240 135
105 1
Colocando os valores obtidos numa tabela, temos:
Quociente
Números que pretendo
Encontrar o m.d.c
240
Resto
1
135
105

4. Como não obtiveste resto zero na divisão de 240 por 135, divides o divisor anterior (135) pelo resto
obtido (105)
135
30
105
1
Completando com estes valores a grelha anterior, fica:
Quociente
1
1
240
135
105
resto
105
30

5. Como não obtiveste resto zero na divisão de 135 por 105, divides o divisor anterior (105) pelo
resto obtido (30)
105
15
30
3
Completando com estes valores a grelha anterior, fica:
Quociente
1
1
3
240
135
105
30
resto
105
30
15

6. Como não obtiveste resto zero na divisão de 105 por 30, divides o divisor anterior (30) pelo
resto obtido (15)
30
15
0
2
Completando com estes valores a grelha anterior, fica:
Quociente
1
1
3
2
240
135
105
30
15
resto
105
30
15
0
Como obtivemos resto zero, significa que o Máximo Divisor Comum (m.d.c) entre 240 e 135
é 15, ou seja, m.d.c (240, 135) = 15
Podemos também concluir que 240, 135, 105, 30 e 15 têm divisores comuns.

7. Já percebi: Para determinar o Máximo Divisor
Comum entre dois números, vou dividindo,
sucessivamente, os divisores pelos restos obtidos até
obter uma divisão em que o resto seja zero (0).
O Máximo Divisor Comum será o divisor da divisão
onde obtive resto zero!
Vamos agora treinar um pouco…
a) Determina o m.d.c (12, 18)
18 12
12
6
6 1
0
2
Q
1
2
18 12
6
R
0
6
O m.d.c entre 12 e 18 é seis.

8. Vejamos, no caso anterior, se o m.d.c entre 12 e 18 é realmente 6:
D12={1, 2, 3, 4, 6, 12}
D18={1, 2, 3, 6, 9, 18}
6 é portanto o maior divisor comum entre 12 e 18, ou seja,
m.d.c (12, 18) = 6
Quer dizer que sempre que
quiser determinar o m.d.c
entre dois números que
tenham muitos divisores é
mais rápido se o fizer pelo
algoritmo de Euclides!

9. Vamos ver quem
consegue
determinar
primeiro o m.d.c
entre 30 e 200!
Combinado! Eu vou
utilizar o Algoritmo
de Euclides, e tu
determinas os
divisores.
200
D30={1, 2, 3, 5, 6, 10, 15, 30}
D200={1,2,4, 5, 8, 10, 20, 25,
40,50, 100, 200}
m.d.c (30, 200)= 10
30
20
6
20
0
30
20
10
1
10
2
m.d.c(30,200) =10
Quem achas que conseguiu primeiro?