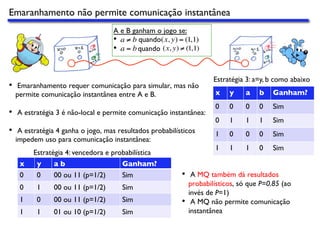
O documento discute a mecânica quântica, enfatizando conceitos como não-localidade quântica, emaranhamento e suas implicações em experimentos, como o jogo do astronauta e Bidu. Ele explora como particulas emaranhadas podem ser utilizadas para superar limitações clássicas na comunicação e no teletransporte quântico. Além disso, menciona aplicações práticas da mecânica quântica, como criptografia quântica e computação distribuída.

1. Não-localidade quântica
Ernesto F. Galvão
Instituto de Física, UFF

2. Física quântica
• Desenvolvida na década de 1920 para descrever sistemas
microscópicos: fótons (luz), elétrons, átomos, etc.
• Muito diferente das teorias físicas anteriores (ditas “clássicas”):
- Descrição probabilística – a teoria só descreve as
probabilidades de qualquer evento ocorrer.
- Possibilidade de “superposição quântica” – combinação
estranha de propriedades contraditórias (como estar em dois lugares
ao mesmo tempo)
- Princípio da Incerteza: medições de uma propriedade muda o
sistema, o que torna impossível determinar precisamente outras
propriedades
- Emaranhamento quântico - correlações surpreendentes entre
propriedades de partículas separadas
Deus não joga
dados!
Fantasmagórica
ação a distância!

3. O que é uma teoria realista local?
• Uma teoria é realista e local se ela:
1- É realista: as propriedades dos sistemas são pré-definidas, independentemente do
processo de medição delas.
Exemplo: Fótons em vidro semi-espelhado.
Cada fóton já “sabe’’ por onde vai sair?
• Exemplos:
• Gravitação universal de Newton não é local;
• mas a Relatividade Geral e o eletromagnetismo de Maxwell são realistas e locais.
• As teorias físicas atuais mais bem-sucedidas são realistas e
locais, com uma exceção: a mecânica quântica
2- É local: nenhuma influência física pode se propagar mais
rapidamente que a luz.

4. O Jogo do Astronauta e Bidu
O Astronauta parte numa missão e Bidu fica na Terra. Estão sem comunicação entre si, mas
eles têm 2 máquinas que programaram com cuidado antes da viagem.
x y a b Ganham?
0 0 1 0 Não
0 1 1 1 Sim
1 0 0 0 Sim
1 1 0 1 Sim
Estratégia 1:A inverte, B não
x y a b Ganham?
0 0 0 0 Sim
0 1 0 0 Sim
1 0 0 0 Sim
1 1 0 0 Não
Estratégia 2: sempre 0
P=3/4 P=3/4
Só há 16 estratégias determinísticas.
A maior probabilidade de
sucesso é P= ¾.
Astronauta (A):
• recebe bit de entrada x
• gera bit de resposta a
Bidu (B):
• recebe bit de entrada y
• gera bit de resposta b
Qual é a maior probabilidade
P de sucesso?
A e B ganham o jogo se:
• quando
• quando
a ≠ b (x, y) = (1,1)
a = b (x, y) ≠ (1,1)

5. O Jogo do Astronauta e Bidu
Astronauta (A):
• recebe bit de entrada x
• gera bit de resposta a
Bidu (B):
• recebe bit de entrada y
• gera bit de resposta b
Qual é a maior probabilidade
P de sucesso?
• Vimos que a maior probabilidade de sucesso é P=3/4.
• Se A e B pudessem se comunicar, P=1.
• E se P>3/4? Melhor desconfiar de A e B:
E se P>3/4 mesmo
sem comunicação?
O Astronauta parte numa missão e Bidu fica na Terra. Estão sem comunicação entre si, mas
eles têm 2 máquinas que programaram com cuidado antes da viagem.
A e B ganham o jogo se:
• quando
• quando
a ≠ b (x, y) = (1,1)
a = b (x, y) ≠ (1,1)

6. Emaranhamento quântico
Astronauta (A):
• bit de entrada x
• bit de resposta a
Bidu (B):
• bit de entrada y
• bit de resposta b
• É possível criar pares de partículas quânticas emaranhadas
(Einstein, Podolsky, Rosen 1935)
A e B ganham o jogo se:
• quando
• quando
a ≠ b (x, y) = (1,1)
a = b (x, y) ≠ (1,1)

7. Emaranhamento quântico
Astronauta (A):
• bit de entrada x
• bit de resposta a
Bidu (B):
• bit de entrada y
• bit de resposta b
• É possível criar pares de partículas quânticas emaranhadas
(Einstein, Podolsky, Rosen 1935)
• Se o Astronauta e Bidu construírem suas caixas com “recheio” de partículas quânticas
emaranhadas, conseguem uma probabilidade de sucesso P=0.85 > 3/4.
• Medições sobre cada partícula de um par terão resultados mais
correlacionados do que a física clássica (local) permite
(John Bell, 1964)
A e B ganham o jogo se:
• quando
• quando
a ≠ b (x, y) = (1,1)
a = b (x, y) ≠ (1,1)

8. Emaranhamento não permite comunicação instantânea
• Emaranhamento requer comunicação para simular, mas não
permite comunicação instantânea entre A e B.
• A estratégia 3 é não-local e permite comunicação instantânea:
• A estratégia 4 ganha o jogo, mas resultados probabilísticos
impedem uso para comunicação instantânea:
x y a b Ganham?
0 0 0 0 Sim
0 1 1 1 Sim
1 0 0 0 Sim
1 1 1 0 Sim
Estratégia 3: a=y, b como abaixo
x y a b Ganham?
0 0 00 ou 11 (p=1/2) Sim
0 1 00 ou 11 (p=1/2) Sim
1 0 00 ou 11 (p=1/2) Sim
1 1 01 ou 10 (p=1/2) Sim
• A MQ também dá resultados
probabilísticos, só que P=0.85 (ao
invés de P=1)
• A MQ não permite comunicação
instantânea
Estratégia 4: vencedora e probabilística
A e B ganham o jogo se:
• quando
• quando
a ≠ b (x, y) = (1,1)
a = b (x, y) ≠ (1,1)

9. Não-localidade na mecânica quântica
• A e B conseguem P=0.85 com caixas quânticas. Para fazer isso com caixas clássicas, só com
comunicação.
• Apesar disso, as caixas quânticas não permitem comunicação entre A e B.
• Como “sabotar” essa influência misteriosa a distância?
• Experimentalmente, já se mostrou que mesmo medidas simultâneas em A e B continuam
revelando essas correlações quânticas, isto é, P=0.85 mesmo assim.
A Natureza viola o princípio do realismo local
• Essa não-localidade quântica permanece um dos maiores mistérios da física.

10. Criando fótons emaranhados
• Processo de conversão paramétrica descendente num cristal não-linear:
• Os dois fótons emaranhados saem nos pontos A e B da figura.€
ψ AB
=
1
2
h A
v B
+ v A
h B( )
A
B
• Fótons emaranhados já foram distribuidos e testados a distâncias de até 143 Km, entre duas
das Ilhas Canárias:
A ideia é aperfeiçoar a tecnologia para
distribuir emaranhamento via satélite

11. Aplicações de estados emaranhados
• Medidas em estados emaranhados são úteis para melhorar o desempenho de certas tarefas
envolvendo comunicação, ou mesmo realizar tarefas impossíveis classicamente.
Teletransporte quântico – recupera estado quântico à distância, usando
emaranhamento e comunicação clássica
(Bennett, Brassard, Crepeau, Jozsa, Peres,Wootters 1993)
Complexidade de comunicação - menos comunicação em problemas computacionais
distribuídos (Cleve, van Dam, Nielsen, Tapp 1997)
Criptografia quântica – segurança absoluta usando teste de Bell (Ekert 1991)
Geradores de números aleatórios
Computação quântica

12. Teletransporte
Teletransporte: equivale a conjunto perfeito de scanner/impressora.
Scanner Impressora 3D
Informação
clássica
Problema: não dá para obter toda a informação de uma única cópia de sistema quântico –
(Princípio da Incerteza de Heisenberg)
Redefinindo a tarefa: eu só quero fazer uma copiadora quântica perfeita, sem tentar
obter/transmitir informação sobre o original.

13. Copiadoras quânticas
Copiadora quântica: usa evolução quântica (unitária) para criar cópias de um sistema
quântico.
Copiadora

14. Copiadoras quânticas
Copiadora quântica: usa evolução quântica (unitária) para criar cópias de um sistema
quântico.
Copiadora
Problema: não dá!
Teorema da não clonagem – Wootters/Zurek (1982).

15. Copiadora quântica (quantum cloning machine): usa evolução quântica (unitária) para criar
cópias imperfeitas de um sistema quântico.
Copiadora
imperfeita
Copiadoras imperfeitas são possíveis – os limites são impostos pela MQ
Copiadoras quânticas

16. Precisamos recriar à distância estado original, destruindo-o e sem obter nenhuma
informação sobre ele.
Impossível classicamente, mas possível se usarmos efeitos quânticos.
Teletransporte quântico

17. Precisamos recriar à distância estado original, destruindo-o e sem obter nenhuma
informação sobre ele.
Impossível classicamente, mas possível se usarmos efeitos quânticos.
Par de sistemas
emaranhados
Protocolo de teletransporte: (Bennett et al., 1993)
1- A e B dispõem de par de partículas emaranhadas.
Teletransporte quântico

18. Precisamos recriar à distância estado original, destruindo-o e sem obter nenhuma
informação sobre ele.
Impossível classicamente, mas possível se usarmos efeitos quânticos.
Protocolo de teletransporte: (Bennett et al., 1993)
1- A e B dispõem de par de partículas emaranhadas.
2- A faz medida conjunta em [original + uma perna do par].
Teletransporte quântico

19. Precisamos recriar à distância estado original, destruindo-o e sem obter nenhuma
informação sobre ele.
Impossível classicamente, mas possível se usarmos efeitos quânticos.
Protocolo de teletransporte: (Bennett et al., 1993)
1- A e B dispõem de par de partículas emaranhadas.
2- A faz medida conjunta em [original + uma perna do par].
Teletransporte quântico

20. Precisamos recriar à distância estado original, destruindo-o e sem obter nenhuma
informação sobre ele.
Impossível classicamente, mas possível se usarmos efeitos quânticos.
?
Protocolo de teletransporte: (Bennett et al., 1993)
1- A e B dispõem de par de partículas emaranhadas.
2- A faz medida conjunta em [original + uma perna do par].
Teletransporte quântico

21. Precisamos recriar à distância estado original, destruindo-o e sem obter nenhuma
informação sobre ele.
Impossível classicamente, mas possível se usarmos efeitos quânticos.
?
Protocolo de teletransporte: (Bennett et al., 1993)
1- A e B dispõem de par de partículas emaranhadas.
2- A faz medida conjunta em [original + uma perna do par].
3- A diz a B o resultado da medida, que B usa para aplicar unitário que faz seu sistema
assumir o estado do original.
Comunicação clássica
Teletransporte quântico

22. Precisamos recriar à distância estado original, destruindo-o e sem obter nenhuma
informação sobre ele.
Impossível classicamente, mas possível se usarmos efeitos quânticos.
?
Protocolo de teletransporte: (Bennett et al., 1993)
1- A e B dispõem de par de partículas emaranhadas.
2- A faz medida conjunta em [original + uma perna do par].
3- A diz a B o resultado da medida, que B usa para aplicar unitário que faz seu sistema
assumir o estado do original.
Comunicação clássica
Teletransporte quântico

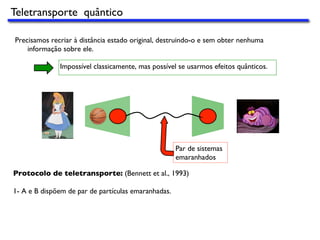
23. Precisamos recriar à distância estado original, destruindo-o e sem obter nenhuma
informação sobre ele.
Impossível classicamente, mas possível se usarmos efeitos quânticos.
Protocolo de teletransporte: (Bennett et al., 1993)
1- A e B dispõem de par de partículas emaranhadas.
2- A faz medida conjunta em [original + uma perna do par].
3- A diz a B o resultado da medida, que B usa para aplicar unitário que faz seu sistema
assumir o estado do original.
Teletransporte quântico

24. • Complexidade de comunicação: cada pessoa tem parte dos dados, e Clara precisa
calcular f(x,y,z). Qual o mínimo de comunicação necessária entre as pessoas?
x z
y
A
B
C
f(x,y,z)?
• Aplicações: design de circuitos eletrônicos, computação em rede
• Vantagem quântica: usamos emaranhamento ao invés de comunicação
x z
y
A
B
C
Solução clássica Solução quântica
Computação distribuída

25. • O emaranhamento é importante para obtermos vantagens no processamento quântico de
informação.
• Vários protótipos de computadores quânticos têm demonstrado essa vantagem.
• Por exemplo, eu tenho colaborado com grupos experimentais italianos na implementação
de pequenos computadores fotônicos:
Computação quântica

26. Sugestões de leitura
A face oculta da Natureza: o novo mundo da física
quântica Anton Zeilinger (Ed. Globo - 2005)
O que é computação quântica?
Ernesto F. Galvão (Ed.Vieira&Lent – 2007)
A revolução dos q-bits
Ivan Oliveira e Cássio Leite (Zahar – 2009)
Obrigado pela atenção!