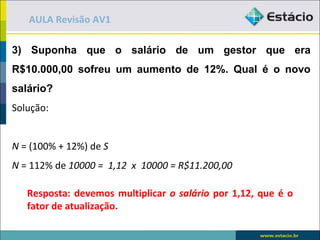
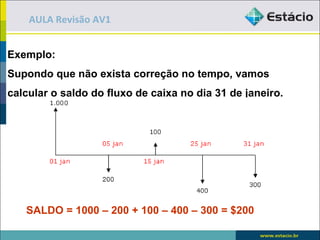
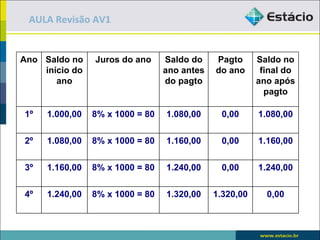
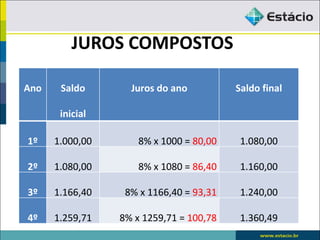
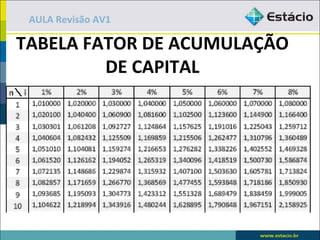
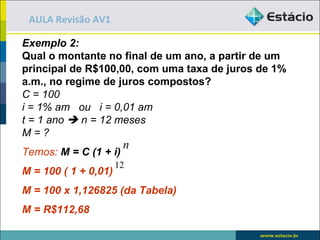
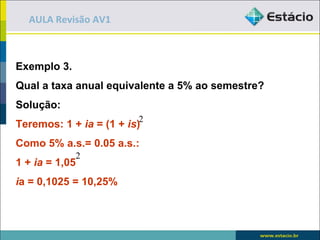
O documento apresenta exemplos e exercícios sobre porcentagem, juros simples, juros compostos e fluxo de caixa. No primeiro exemplo, é calculado 15% de 120. Nos exercícios seguintes, são resolvidos problemas envolvendo cálculo de porcentagens, taxa de juros, montante e fator de acumulação.

1. MATEMÁTICA FINANCEIRA
LUIZ ROBERTO
Rio de Janeiro, 27 de agosto de 2011

2. AULA Revisão AV1
AULA
Revisão AV1

3. AULA Revisão AV1
REVISÃO DE PORCENTAGEM
p
À taxa porcentual p% associamos a razão
100
Assim, calcular p% de uma quantidade qualquer é
p
multiplicá-la pela razão 100 .
Exemplo 1:
Calcular 15% de 120.
15
15% = = 0,15  forma unitária
100
Então: 15% de 120 = 0,15 x 120 = 18

4. AULA Revisão AV1
2
• Escreva na forma porcentual.
5
2 4 40
= 0,4 = = = 40%
5 10 100
Portanto,
2 significa 40%.
5

5. AULA Revisão AV1
PROBLEMAS DE PORCENTAGEM
1) Um serviço com preço R$840,00 foi reajustado
para R$1.092,00. Qual o porcentual de aumento?
Solução:
O produto passou de 840  1092
Aumentou em: 252
p
. 840 = 252 logo p = 100.252 = 30
100 840
Resposta: aumento de 30%

6. AULA Revisão AV1
2) Um frete com preço R$1.092,00 teve uma redução no seu
preço para R$840,00. Qual o porcentual relativo a essa
redução?
Solução:
O frete passou de 1092  840
Redução de 252
Vamos procurar o porcentual de 1092 que corresponde a 252:
p
. 1092 = 252 logo p = 100.252 = 23,07
100 1092
Resposta: redução de 23,07%

7. AULA Revisão AV1
3) Suponha que o salário de um gestor que era
R$10.000,00 sofreu um aumento de 12%. Qual é o novo
salário?
Solução:
N = (100% + 12%) de S
N = 112% de 10000 = 1,12 x 10000 = R$11.200,00
Resposta: devemos multiplicar o salário por 1,12, que é o
fator de atualização.

8. AULA Revisão AV1
4) Qual o valor para o fator acumulado após reajustes
consecutivos em um determinado serviço de:
5%, – 3% e 3%?
Solução: Acumula %  multiplica fatores
1,05 x 0,97 x 1,03 = 1,049

9. AULA Revisão AV1
5) O preço de uma TV teve reajustes mensais sucessivos,
gerando um acumulado de 13%. Se o percentual de
aumento do primeiro mês foi de 7%, qual foi o percentual
de reajuste do segundo mês?
Solução: Desconto %  divide fatores
1,13 / 1,07 = 1,056

10. AULA Revisão AV1
Em 1º janeiro de 2010 apliquei R$12.000,00 na poupança.
Suponha que o rendimento em 2010 foi de 8%.
Qual será o saldo em 1° de janeiro de 2011?
Solução:
Correção do valor do dinheiro no período:
6% de 1000 = 0,08 . 12000 = 960
1 jan 2010 1 jan 2011 Resp:
Saldo em 01/11/2011:
12.000 + 960 = R$12.960,00
R$12.000 ?

11. AULA Revisão AV1
Exercício 1:
Supondo que em certo trimestre a inflação foi de 6%, 8% e
10% ao mês, respectivamente, qual a inflação acumulada no
trimestre?

12. AULA Revisão AV1
solução:
Aplicando fatores de atualização:
1º mês 6% 1,06
2º mês 8% 1,08
3º mês 10% 1,10
Fator acumulado: 1,06 . 1,08 . 1,10 = 1,25928
Logo, o índice de correção é: 25,928%
Acumula %  multiplica fatores

13. AULA Revisão AV1
Exercício 2:
Um frete teve reajuste acumulado em um bimestre de
38%. Se no 1º mês o aumento foi de 20%, qual o
aumento do 2º mês?
Pelo FA:
100
+20%
120
?% 1º mês FA = 1,2
+20 +18
2º mês FA= ?
+38%
Bimestre FA = 1,38
Então, 1,2 x = 1,38 logo: x = 1,38 / 1,2 = 15%
desconto %  divide fatores

14. AULA Revisão AV1
Exercício 3:
Certa categoria profissional conseguiu para junho reajuste de
62% sobre o salário de janeiro, descontadas as antecipações.
Como houve um adiantamento de 25% em março, que % deve
incidir sobre os salários de março?
Devemos descontar dos
Jan Mar Jun
62,5% o adiantamento de
+25% ?%
100 125 162,5
25%. Se x é o fator relativo
ao novo ajuste:
Então: x = 1,625 / 1,25 = 1,3 ou 30%

15. AULA Revisão AV1
FLUXO DE CAIXA
O fluxo de caixa (cash flow), refere-se ao montante
recebido e gasto durante um período de tempo definido.
Tipos de fluxos:
- outflow, de saída, que representa as saídas de capital,
referentes às despesas de investimento.
- inflow, de entrada, que é o resultado do investimento. (Ex:
vendas, redução de custos etc).

16. AULA Revisão AV1
Exemplo:
Supondo que não exista correção no tempo, vamos
calcular o saldo do fluxo de caixa no dia 31 de janeiro.
SALDO = 1000 – 200 + 100 – 400 – 300 = $200

17. AULA Revisão AV1
A taxa de juros é indicada per uma porcentagem (%).
Exemplo:
A compra de um equipamento de preço à vista R$10.000,00,
paga com um cheque pré-datado para 30 dias R$10.500,00.
Vamos calcular a taxa de juros cobrada pela loja.
Valor pago a mais em um mês:
10500 – 10000 = 500 (representa os juros)
500
Porcentagem dos juros: = 5%
10000

18. AULA Revisão AV1
JUROS SIMPLES
Um investidor aplicou $1.000,00 no mercado financeiro,
pelo prazo de quatro anos, a uma taxa de juros simples de
8% ao ano. Calcule o saldo no final de cada quatro anos da
operação.
C = 1000
t=4a
i = 8% aa

19. AULA Revisão AV1
Ano Saldo no Juros do ano Saldo do Pagto Saldo no
início do ano antes do ano final do
ano do pagto ano após
pagto
1º 1.000,00 8% x 1000 = 80 1.080,00 0,00 1.080,00
2º 1.080,00 8% x 1000 = 80 1.160,00 0,00 1.160,00
3º 1.160,00 8% x 1000 = 80 1.240,00 0,00 1.240,00
4º 1.240,00 8% x 1000 = 80 1.320,00 1.320,00 0,00

20. AULA Revisão AV1
JUROS SIMPLES
Fórmula dos juros simples:
cit
j=
100
onde i referida na mesma unidade de t
Exemplo:
i = 15% aa ; t = 3 anos
i = 2% am ; t = 15 meses

21. AULA Revisão AV1
MONTANTE
O Montante é a soma do capital (C) com os juros (J).
M=C+J

22. AULA Revisão AV1
MONTANTE - EXERCÍCIOS
Se R$3.000,00 foram aplicados por 5 meses à taxa de juros
simples de 4% ao mês, determine:
a) os juros recebidos; b) o montante M
C = 3000 t=5m i = 4% am
cit 3000.4.5
j= = = R$600
100 100
M = 3000 + 600 = R$3600,00

23. AULA Revisão AV1
MONTANTE - EXERCÍCIOS
A quantia de R$2.000,00 foi aplicada por sete meses a juros simples de
taxa anual 24%. Qual o montante dessa aplicação?
24
C = 2000 t=7m i = 24% aa = = 2% am
12
24% aa e 2% am são taxas equivalentes a juros simples.
Assim: 7 x 2% = 14%
M = 1,14 x 2000 = R$2.280,00

24. AULA Revisão AV1
JUROS COMPOSTOS
A remuneração que o capital C recebe após n
períodos de aplicação, quando a cada período, a
partir do segundo, os juros são calculados sobre o
montante do capital C no período anterior.

25. AULA Revisão AV1
JUROS COMPOSTOS
Exemplo:
Um investidor aplicou em um Banco R$1.000,00 a
uma taxa de juros compostos de 8% ao ano.
Calcule o valor do saldo credor no final de cada
um dos quatro anos da operação.

26. JUROS COMPOSTOS
Ano Saldo Juros do ano Saldo final
inicial
1º 1.000,00 8% x 1000 = 80,00 1.080,00
2º 1.080,00 8% x 1080 = 86,40 1.160,00
3º 1.166,40 8% x 1166,40 = 93,31 1.240,00
4º 1.259,71 8% x 1259,71 = 100,78 1.360,49

27. AULA Revisão AV1
MONTANTE
O Montante M de um capital C aplicado à taxa i de juros
compostos, a cada período, por n períodos, é dado por:
M = C (1 + i ) n
(1 + i ) n é o de fator de capitalização ou
fator de acumulação.

28. AULA Revisão AV1
TABELA FATOR DE ACUMULAÇÃO
DE CAPITAL

29. AULA Revisão AV1
Exemplo 1:
Qual o montante produzido por R$10.000,00 à taxa de
juros compostos de 6% ao mês, durante 5 meses.
M=?
C = 10000
i = 6% am = 6/100 = 0,06 am (taxa unitária)
n = 5 (i e t estão na mesma unidade de tempo)
Aplicando a fórmula dos juros compostos:
M = C (1 + i )n = 10000 (1,06)5
Para a taxa 6% e n = 5, encontramos 1,338225
Logo:
M = 10000 x 1.338225 = R$13.282,25

30. AULA Revisão AV1
Exemplo 2.
Calcular o montante da aplicação de R$10.000,00 à taxa
composta de 8% ao trimestre durante um ano.
M=?
C = 10000
i = 8% a.t. = 0,08 a.t.
t = 1 ano
O período de capitalização é trimestral (juros a cada trimestre).
Logo, t = 1 ano  n = 4
M = C (1 + i )n = 10000 x (1,08)4
M = 10000 x 1,360488 (Tab. Fator Acumulação de Capital)
M = 13604,88 = R$13.604,88

31. AULA Revisão AV1
TAXA EQUIVALENTE
Seja o capital C aplicado por um ano a uma taxa anual ia.
O montante M ao final do período de 1 ano será igual a
M = C (1 + ia)
Consideremos agora, o mesmo capital M aplicado por 12
meses a uma taxa mensal im.
O montante M’ ao final do período de 12 meses será:
12
M’ = C (1 + im)

32. AULA Revisão AV1
Exemplo 1:
Seja:
im = 1% am (Período mês)
Qual a taxa equivalente ao ano (ia % aa )? (Período ano)
(1 + ia ) = ( 1 + im)12
12
(1 + ia ) = ( 1 + 0,01)
(1 + ia) = 1.1268 (da Tabela)
Logo: ia = 1,1268 -1 = 0,1268 ou 12,68% aa

33. AULA Revisão AV1
Exemplo 2:
Qual o montante no final de um ano, a partir de um
principal de R$100,00, com uma taxa de juros de 1%
a.m., no regime de juros compostos?
C = 100
i = 1% am ou i = 0,01 am
t = 1 ano  n = 12 meses
M=?
n
Temos: M = C (1 + i)
12
M = 100 ( 1 + 0,01)
M = 100 x 1,126825 (da Tabela)
M = R$112,68

34. AULA Revisão AV1
Exemplo 3.
Qual a taxa anual equivalente a 5% ao semestre?
Solução:
2
Teremos: 1 + ia = (1 + is)
Como 5% a.s.= 0.05 a.s.:
2
1 + ia = 1,05
ia = 0,1025 = 10,25%