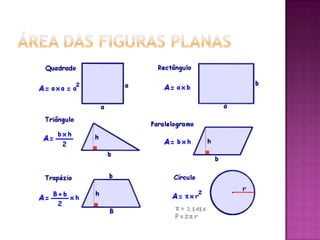
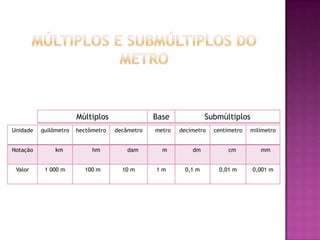
O documento discute a relevância da matemática nas atividades cotidianas, especialmente no cálculo de áreas e medidas de comprimento. Utiliza exemplos práticos, como a reforma de uma sala e a compra de lajotas, para ilustrar a necessidade de converter unidades de medida. Além disso, propõe problemas para exercitar a compreensão sobre múltiplos e submúltiplos do metro.

1. Matemática na ÁreaMedidas de ComprimentoMúltiplos e Submúltiplos do metro

2. Daiane Gomes BuenoPós graduando em Novas Tecnologias no Ensino da Matemática

3. Você já se atentou ao fato de quanto a Matemática está presente no nosso cotidiano?Veja:

4. Ainda não encontrou relação entre a Matemática e sua vida?Olhe agora:

5. Muitas vezes temos que realizar determinados cálculos matemáticos para resolver questões do dia-a-dia, como por exemplo, comprar um piso para colocar em um cômodo da casa.Para entender melhor, conheça um pouco sobre as figuras geométricas.

6. Área das figuras planas

7. Agora que você já conheceu como podemos calcular a área de uma dada figura, imagine a seguinte situação:Antônio irá reformar o piso da sala de sua residência. A sala tem formato quadrado, de lado medindo 5 m. Se ele pretende utilizar lajotas quadradas de lado medindo 0,5 m, quantas lajotas serão necessárias para cobrir todo o piso da sala?Resposta: 100 lajotasMedida da área da sala : 5² = 25 metrosMedida da área da lajota: 0,5² =0,25 metrosLogo: 25 : 0,25 = 100 lajotas.

8. O problema que Antônio estava enfrentando faz parte da nossa realidade e para resolvê-lo foi preciso conhecimento a respeito de áreas, medidas e operações.Sempre que temos a necessidade de calcular áreas, nos deparamos com as medidas de comprimento. Porém, nem sempre as medidas estão representadas na mesma unidade e isto pode dificultar o cálculo de área, obtendo assim um resultado errôneo.Vamos então, conhecer as unidades de medida que se relacionam diretamente com o metro.

9. Múltiplos e Submúltiplos do metro

10. Quando nos deparamos com unidades de medidas diferentes entre si, é necessário transformá-las para que todas fiquem com mesma unidade e assim seja possível efetuar o cálculo necessário.Para transformar as medidas de comprimento de uma unidade em outra, usamos a seguinte regra prática: :10 :10 :10 :10 :10 :10 km hm damm dm cm mm x10 x10 x10 x10x10x10

11. No esquema:Para transformar unidades maiores em unidades menores, multiplicamos por 10.Para transformar unidades menores em unidades maiores, dividimos por 10.Agora, resolva o seguinte problema:

12. Pense e resolva:Pedro ,Carlos e Ana estão indo para a escola pelo mesmo caminho. Pedro já caminhou 0,6 km, Carlos caminhou 30 000 cm e Ana, 500 m.a)Qual criança andou mais?b)Quantos metros faltam para a última criança alcançar a que andou mais?c)Se a escola fica a 700 m da casa das crianças, quantos metros faltam para cada criança chegar à escola?

13. Este pode parecer um problema bem simples, mas acreditem, para muitos de nossos alunos, torna-se algo de difícil resolução.Até a próxima.

14. referências:projeto araribá: Matemática / obra coletiva, concebida, desenvolvida e produzida pela Editora Moderna. – 1 ed. – são paulo : Moderna, 2006.images.google.com.br/