O documento descreve os princípios do projeto e execução de lajes protendidas, incluindo os materiais e sistemas de protensão utilizados. Aborda conceitos como protensão completa, limitada e parcial, além de apresentar recomendações sobre dimensionamento de acordo com a agressividade ambiental.


![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 1
________________________________________________________________________________
Engº. Alexandre Emerick
PROJETO E EXECUÇÃO DE
LAJES PROTENDIDAS
1. INTRODUÇÃO
O uso da solução em concreto protendido para lajes de edifícios tem crescido nos últimos anos
no Brasil. Fenômeno esse que se deve em grande parte à utilização do sistema de protensão
não-aderente com a entrada da monocordoalha engraxada plastificada no mercado brasileiro.
Segundo Franco [11]
o concreto protendido vem encontrando uma aplicação cada vez maior em
estruturas de edifícios devido à necessidade de vencer vãos livres de grandes dimensões com
elementos de altura reduzida.
A utilização do sistema de protensão com pós-tração em lajes apresenta algumas vantagens
em relação ao sistema convencional em concreto armado, entre as quais cabe citar:
• Maior liberdade arquitetônica devido à possibilidade de vencer grandes vãos ou vãos
fortemente carregados mantendo uma grande esbeltez na laje.
• Maior área útil do pavimento devido a menor quantidade de pilares.
• Economia em relação às estruturas em concreto armado para vãos superiores a 7,0 m
conforme ilustra a Figura 1.1 extraída da referência [35].
• Redução nas espessuras das lajes acarretando uma significativa diminuição na altura total
do prédio e conseqüentemente um menor peso total da estrutura minimizando os custos
nas fundações.
• Maior velocidade na desforma e retirada de escoramentos.
• Redução e até eliminação de flechas e fissuração nas lajes.
• Maior resistência ao puncionamento, em lajes lisas ou cogumelo, obtida pela colocação
adequada dos cabos de protensão nas regiões próximas aos pilares.
Figura 1.1: Comparação de custos entre lajes protendidas e convencionais em concreto
armado
Fonte: Ref. [35]
2. PRINCÍPIO DA PROTENSÃO
De acordo com Moraes [19]
, as normas atuais definem como peças estruturais de concreto
protendido as peças de concreto nas quais através da introdução de forças torna-se
comprimido de tal forma a eliminar as tensões de tração quando colocada em serviço, ou
ainda, eliminar apenas uma parcela dessas tensões.
7 m 8 m 9 m 10 m
VÃO
CUSTO
LAJE PROTENDIDA
LAJE EM CONCRETO ARMADO
60
50
70
80
90
100](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-3-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 2
________________________________________________________________________________
Engº. Alexandre Emerick
A Figura 2.1 ilustra a ação da protensão nas tensões atuante no concreto considerando
protensão completa, ou seja, eliminando totalmente as tensões de tração na peça em serviço.
Figura 2.1: Tensões atuantes no concreto protendido – protensão completa.
Segundo Moraes [19]
, a eliminação das tensões de tração que podem dar origem à formação de
fissuras representava o principal objetivo da protensão, obtendo-se uma construção de maior
qualidade reduzindo-se o perigo da corrosão através da protensão completa. Modernamente,
com o desenvolvimento da teoria de fissuração, tornou-se possível conviver com o controle da
abertura de fissuras, obtendo construções satisfatórias com custos menores, admitindo-se o
Estado Limite de Utilização.
De acordo com a NBR 7197 [23]
a protensão pode ser completa, limitada ou parcial de acordo
com as definições a seguir:
• Protensão completa: Existe protensão completa quando se verificam as duas condições
seguintes:
a) para as combinações freqüentes de ações, previstas no projeto, é respeitado o Estado
Limite de Descompressão;
b) para as combinações raras de ações, quando previstas no projeto, é respeitado o
Estado Limite de Formação de Fissuras.
• Protensão limitada: Existe protensão limitada quando se verificam as duas condições
seguintes:
a) para as combinações quase permanentes de ações, previstas no projeto, é respeitado o
Estado Limite de Descompressão;
b) para as combinações freqüentes de ações, previstas no projeto, é respeitado o Estado
Limite de Formação de Fissuras.
• Protensão parcial: Existe protensão parcial quando se verificam as duas condições
seguintes:
a) para as combinações quase permanentes de ações, previstas no projeto, é respeitado o
Estado Limite de Descompressão;
b) para as combinações freqüentes de ações, previstas no projeto, é respeitado o Estado
Limite de Abertura de Fissuras com abertura característica menor ou igual a 0,2 mm.
O projeto de revisão da NB-1 (NBR 6118) [22]
classifica os níveis de protensão permitidos em
função da classe de agressividade ambiental definidos no item 9.4 dessa norma. A Tabela 2.1
extraída do PR NB-1 relaciona os níveis de protensão com as classe de agressividade
ambiental e as exigências quanto aos Estados Limites relacionados com o nível de fissuração
permitido.
=
A
P
−
W
Pe
W
MEXT
−
W
Pe
A
P
W
MEXT
I −+=σ
W
Pe
A
P
W
MEXT
S +−−=σ
P
e
MEXT
(+)
(−) (+)
(−)
(−)+ + (−)](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-4-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 3
________________________________________________________________________________
Engº. Alexandre Emerick
Tabela 2.1: Classes de agressividade ambiental e exigências relativas à fissuração excessiva e
a proteção da armadura ativa
Tipos de concreto
estrutural
Classe de
agressividade
ambiental
Exigências relativas
ao E.L. de fissuração
excessiva
Combinação de
ações a considerar
Concreto simples
(sem protensão e sem
armadura)
I a IV Não há –
I
ELS-W
ωk ≤ 0,4mm
Freqüente
Concreto armado
(sem protensão)
II a IV
ELS-W
ωk ≤ 0,3mm
Freqüente
ELS-W
ωk ≤ 0,2mm
FreqüenteConcreto protendido
nível 1
(protensão parcial)
Pré-tração – I
Pós-Tração – I e II
ELS-F Quase permanente
ELS-F Freqüente
Concreto protendido
nível 2
(protensão limitada)
Pré-tração – II
Pós-Tração – III e IV
ELS-D Quase permanente
ELS-F RaraConcreto protendido
nível 3
(protensão completa)
Pré-tração
III e IV ELS-D Freqüente
Fonte: Projeto de revisão da NB-1 [22]
onde:
ELS-W – Estado Limite de Serviço – Abertura de fissuras;
ELS-F – Estado Limite de Serviço – Formação de fissuras;
ELS-D – Estado Limite de Serviço – Descompressão;
Classe de agressividade:
I – fraca;
II – média;
III – forte;
IV – muito forte.
Dessa forma, de acordo com a Tabela 2.1, o PR NB-1 prescreve com relação a protensão
parcial que para a combinação quase permanente das ações seja respeitado o Estado Limite
de Formação de Fissuras (ELS-F), sendo portanto, menos rigorosa que a NBR 7197 [23]
, pois
admite um pequeno nível de tração no concreto para a combinação quase permanente das
ações.](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-5-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 4
________________________________________________________________________________
Engº. Alexandre Emerick
3. MATERIAIS UTILIZADOS EM LAJES PROTENDIDAS
Existem basicamente dois sistemas de protensão com pós-tração empregados em lajes
protendidas em função da aderência ou não entre o cabo e o concreto:
3.1. PROTENSÃO ADERENTE
Neste caso, os cabos são colocados dentro de bainhas metálicas, sendo essas injetadas com
nata de cimento após a operação de protensão das cordoalhas. A solução com cordoalhas
aderentes comporta-se melhor quanto à distribuição das fissuras e à segurança à ruptura para
efeitos localizados (explosão, incêndios, demolição parcial, etc.).
Entre os aços de protensão existentes atualmente distinguem-se os aços de relaxação normal
(RN) e os de relaxação baixa (RB). Com relação à sua resistência a tração os mais comuns
são o CP-175 e CP-190. Entretanto, nas obras com lajes protendidas o aço que vem sendo
mais largamente empregado é o CP-190 RB, tanto para a protensão com ou sem aderência. A
Tabela 3.1 apresenta as características técnicas das cordoalhas com aço CP-190 RB.
Tabela 3.1: Propriedades das cordoalhas de 7 fios – Aço CP190 RB
Tipo de cordoalha ∅∅∅∅12,7mm (1/2”) ∅∅∅∅15,2mm (5/8”)
Área mínima (mm2
)(1)
98,7 140,0
Área aproximada (mm2
) 101,4 143,5
Massa nominal (kg/m) 0,775 1,102
Carga de ruptura − fptk (kN) 187,3 265,8
Tensão de escoamento – fpyk (MPa) 1585 1688
Módulo de Elasticidade (GPa) Aproximadamente 196
Relaxação após 1000 horas a 20ºC para
carga inicial de 70% da ruptura
MÁX. 2,5%
Fonte: Ref. [5]
_______________________
NOTA: 1. A área mínima deve ser considerada no cálculo
A Tabela 3.2 apresenta as propriedades das bainhas achatadas para cordoalhas no sistema de
protensão com aderência extraída da referência [35].
Tabela 3.2: Propriedades das bainhas chatas corrugadas
Tipo de
cabo
H
(mm)
B
(mm)
Peso
linear
(kg/m)
Consumo
de cimento
p/ injeção
(kg/m)
Consumo
de calda
(L/m)
1 ∅ 12,7 19 35 0,41 0,80 0,58
2 ∅ 12,7 19 35 0,41 0,67 0,48
3 ∅ 12,7 19 69 0,60 1,43 1,03
4 ∅ 12,7 19 69 0,60 1,30 0,93
1 ∅ 15,2 21 35 0,43 0,90 0,65
2 ∅ 15,2 21 69 0,62 1,77 1,28
3 ∅ 15,2 21 69 0,62 1,56 1,13
4 ∅ 15,2 21 75 0,68 1,55 1,12
Fonte: Ref. [35]
Os dispositivos de fixação das extremidades dos cabos são chamados de ancoragens. Essas
ancoragens podem ser ativas, quando permite a operação de protender os cabos, ou passiva
quando é fixa. Em geral, costuma-se projetar cabos com uma ancoragem ativa e outra passiva.
Entretanto, especialmente para cabos longos, comprimentos maiores que 40 metros, pode ser
B
H
Figura 3.1: Dimensões
externas para bainhas
achatadas](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-6-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 5
________________________________________________________________________________
Engº. Alexandre Emerick
CORTE A-A
S/ ESC.
VISTA EM PLANTA
S/ ESC.
Figura 3.3: Ancoragem ativa com armadura de
fretagem para cabos com 4 cordoalhas
Fonte: Ref. [35]
conveniente aplicar a protensão pelas duas extremidades do cabo, utilizando assim ancoragem
ativa nas duas extremidades, de modo a reduzir as perdas por atrito.
A Tabela 3.3 apresenta as dimensões dos nichos das ancoragens ativas do sistema de
protensão aderente extraídas da referência [35].
Tabela 3.3: Dimensões dos nichos das ancoragens ativas – protensão aderente
Unidade de
protensão
A
(mm)
B
(mm)
a
(mm)
b
(mm)
1 ∅12,7 120 120 100 100
2 ∅12,7 120 120 100 100
3 ∅12,7 180 150 130 130
4 ∅12,7 240 100 230 85
1 ∅15,2 140 140 120 120
2 ∅15,2 180 180 140 140
3 ∅15,2 220 220 160 160
4 ∅15,2 240 120 230 90
a
A
b
B
Figura 3.2: Nichos para
ancoragens ativas](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-7-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 6
________________________________________________________________________________
Engº. Alexandre Emerick
As ancoragens passivas podem ser em laço ou em bulbo conforme indicam as Figuras 3.4 e
3.5.
Figura 3.4: Ancoragem passiva em laço com armadura de fretagem
Fonte: Ref. [35]
Tabela 3.4: Dimensões para as ancoragens passivas em laço
Tipo A
(mm)
B
(mm)
1 ∅12,7 600 −
2 ∅12,7 600 −
4 ∅12,7 700 50
1 ∅15,2 600 −
2 ∅15,2 600 −
4 ∅15,2 700 50
Fonte: Ref. [35]
Tabela 3.5: Dimensões para as
ancoragens passivas em bulbo
Tipo A
(mm)
B
(mm)
C
(mm)
4 ∅12,7 310 70 750
4 ∅15,2 390 90 950
Fonte: Ref. [35]
Figura 3.5: Ancoragem passiva em bulbo
Fonte: Ref. [35]](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-8-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 7
________________________________________________________________________________
Engº. Alexandre Emerick
A finalidade da injeção é garantir uma proteção eficaz das armaduras de protensão contra a
corrosão, além de permitir perfeita ligação mecânica da armadura e o concreto, preenchendo
assim os vazios existentes entre a armadura e a parede da bainha. A nata de injeção deve ser
dosada com vistas a atender as seguintes características:
• ausência de agentes agressivos
• fluidez
• exsudação
• expansão
• retração
• resistência mecânica
• pouca absorção capilar
• tempo de início e fim de pega adequados
Para garantir essas características devem ser utilizados cimentos com:
• teor composto ≤ 10%
• teor de enxofre de sulfetos ≤ 0,2%
• teor de cloro de cloretos ≤ 0,1%
A água deve ser potável com uma porcentagem de cloro inferior a 500 mg/L e isenta de
detergentes. Os aditivos podem ser plastificantes, retardadores de pega e expansores.
Influenciam, ainda, na qualidade de injeção:
• natureza, temperatura e idade do cimento
• temperatura da água
• temperatura ambiente
• condições da mistura
Fonte: Ref. [12]
De modo a facilitar uma boa injeção devem ser adotados os seguintes cuidados:
• colocação de purgadores (respiro para a injeção) cuidadosamente e corretamente
• utilização de luvas de união entre trechos de bainhas que garantem estanqueidade
• perfeita fixação das ancoragens na fôrma
• no caso particular de cabos verticais o uso de dispositivos especiais que facilitem a
injeção
Fonte: Ref. [12]
Para a operação de injeção com tempo quente, temperatura ambiente superior a 30 o
C, a
operação deve ser realizada com cuidados especiais para aumentar a vida útil da nata
diminuindo o índice de fluidez. Portanto é recomendado o uso de aditivos apropriados e água
em baixa temperatura (adicionando-se gelo).
A operação de injeção só deve ser iniciada após a aprovação dos resultados da operação de
protensão.
A Figura 3.6 apresenta um detalhe de uma bainha metálica com purgador usada na protensão
aderente.](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-9-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 8
________________________________________________________________________________
Engº. Alexandre Emerick
Figura 3.6: Bainha metálica com purgador
Fonte: Revista Téchne – Janeiro 1997
3.2. PROTENSÃO NÃO ADERENTE
O sistema de protensão não aderente é feito com cordoalhas engraxadas plastificadas. De
acordo com o catálogo técnico da Belgo [5]
, as cordoalhas engraxadas são as mesmas
cordoalhas tradicionais com a adição de um revestimento de PEAD-polietileno de alta
densidade, impermeável à água, extremamente resistente e durável, extrudado diretamente
sobre a cordoalha já engraxada em toda a sua extensão, o que permite a livre movimentação
da cordoalha em seu interior, Figura 3.7. A graxa e o revestimento de PEAD devem atender as
especificações do PTI (Post-tensioning Institute) [30]
. As bitolas disponíveis são de 12,7 mm e
15,2 mm com massa aproximada (incluindo PEAD e graxa) de 890 kg/km e 1240 kg/km,
respectivamente.
Figura 3.7: Seção da monocordoalha engraxada com 7 fios
Nesse sistema, deve ser dada especial atenção a conservação das cordoalhas, elas devem
estar limpas e livres de corrosão. Rasgos ou falhas da cobertura de PEAD devem ser
reparadas antes do lançamento do concreto com fita plástica para isolar a cordoalhas do
concreto.
Com relação ao sistema de protensão sem aderência, Moraes [19]
faz as seguintes
observações:
PEAD
GRAXA
FIOS DE AÇO
DIÂMETRONOMINAL
1/2”=12,7mm
5/8”=15,2mm](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-10-320.jpg)

![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 10
________________________________________________________________________________
Engº. Alexandre Emerick
Tabela 3.7: Monocordoalhas engraxadas de 7 fios – Aço CP190 RB
Tipo de cordoalha ∅∅∅∅12,7mm (1/2”) ∅∅∅∅15,2mm (3/8”)
Área mínima (mm2
) 98,7 140,0
Área aproximada (mm2
) 101,4 143,5
Peso linear com bainha e graxa (kg/m) 0,89 1,24
Carga de ruptura − fptk (kN) 187,3 265,8
Módulo de elasticidade (GPa) Aproximadamente 196
Alongamento após a ruptura 3,5 %
φ cordoalha + bainha (mm) 15,4 18,1
_______________________
NOTA: 1. A área mínima deve ser considerada no cálculo
A Tabela 3.8 e a Figura 3.8 apresentam as características das ancoragens para
monocordoalhas engraxadas do sistema Freyssinet.
Tabela 3.8: Dimensões para as ancoragens ativas
Tipo ∅∅∅∅ bloco
(mm)
A × B
(mm)
1 ∅12,7 45 100 × 100
1 ∅15,2 52 100 × 100
Fonte: Ref. [35]
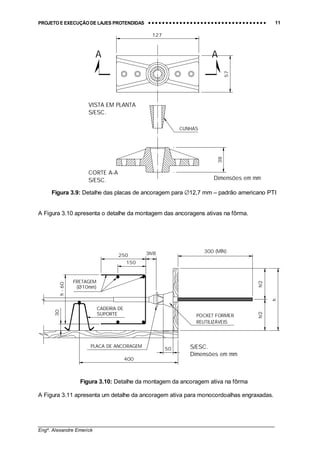
A Figura 3.9 apresenta o detalhe das placas de ancoragem no padrão americano.
Figura 3.8: Ancoragem ativa para monocordoalhas engraxadas
Fonte: Ref. [35]](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-12-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 12
________________________________________________________________________________
Engº. Alexandre Emerick
Figura 3.11: Detalhe dos elementos da ancoragem ativa
Fonte: Ref. [29]
A Figura 3.12 apresenta um esquema típico de montagem de uma laje lisa com
monocordoalhas engraxadas.
Figura 3.12: Esquema típico de montagem de uma laje lisa com monocordoalhas
Fonte: Revista Téchne – Janeiro 1997
FORMA PLÁSTICA REUTILIZÁVEL
(POCKET FORMER)
CUNHA OU CLAVETE
BLOCO DE ANCORAGEM
LUVA
TUBO DE
TRANSIÇÃO](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-14-320.jpg)



![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 16
________________________________________________________________________________
Engº. Alexandre Emerick
A A
CORTE A-A
PLANTA
Figura 4.4: Laje nervurada com faixas protendidas
A A
CORTE A-A
PLANTA
Figura 4.5: Laje nervurada com engrossamento na região dos pilares (capitéis)
De acordo com Cauduro e Leme [8]
, com o uso de lajes planas protendidas a distância entre
pilares pode ser mantida entre 6 e 8 metros sem grandes traumas para a estrutura.
Obviamente, sem vigas os pilares perdem a necessidade de estarem alinhados e também de
ficarem totalmente na parte externa do edifício, aumentando a flexibilidade no lançamento, com](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-18-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 17
________________________________________________________________________________
Engº. Alexandre Emerick
grandes vantagens na obtenção de varandas e fachadas mais simples para serem acabadas.
Vão de 7,6 metros pode ser uma solução bastante interessante em edifícios comerciais, uma
vez que essa distância pode acomodar três carros na garagem eliminando a necessidade de
transições fazendo com que a distância entre pilares se mantenha constante da fundação até a
cobertura. Entretanto, caso seja necessário, pode-se usar transições com vigas chatas ou
capitéis que são mais fáceis de serem executados que as vigas convencionais.
Um ponto importante diz respeito às dimensões dos pilares, deve-se convencer os projetistas
de arquiteturas que pilares com larguras acima de 25 cm permite ganho no cálculo estrutural
além de reduzir o risco de falhas de concretagem nas bases dos pilares, bastante comum nas
estruturas convencionais.
Nas estruturas sem vigas, é necessário recorrer a outros artifícios para garantir a estabilidade
global. Nesses casos, é usual o emprego de paredes estruturais, posicionadas sobretudo nas
caixas de escada e de elevador.
4.2. ESPESSURA DAS LAJES PROTENDIDAS
Para definir a espessura de lajes lisas protendidas em geral busca-se observações práticas. O
ACI 423 [2]
, por exemplo, recomenda adotar os seguintes valores:
• Lajes com sobrecargas entre 2 kN/m2
e 3 kN/m2
:
45
a
40
h
!!
≥
• Lajes de cobertura:
48
a
45
h
!!
≥
Entretanto, nada impede que sejam adotadas espessuras menores desde que sejam
verificados as flechas máximas e o risco de vibração excessiva.
A Figura 4.6 apresenta um gráfico obtido por Schmid [34]
para a determinação da espessura das
lajes cogumelo, em concreto armado ou protendido, com ou sem capitel, para pisos com
sobrecarga total de até 3 kN/m2
(300 kgf/m2
).
Figura 4.6: Esbeltez de lajes cogumelo
Na prática, para o projeto de lajes lisas protendidas com cordoalhas engraxadas têm sido
adotadas as seguintes espessuras, Tabela 4.1:
5 6 7 8 9 10 11 12 13 14 15
10
15
20
25
30
60
!
45
!
40
!
30
!
LAJE COGUMELO (COM CAPITEL) EM C.P.
LAJE LISA (SEM CAPITEL) EM C.P.
LAJE COGUMELO (COM CAPITEL) EM C.A.
LAJE LISA (SEM CAPITEL) EM C.A.
VÃO (m)
ESPESSURA (cm)](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-19-320.jpg)


![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 20
________________________________________________________________________________
Engº. Alexandre Emerick
4.3. MODULAÇÃO DOS VÃOS
Como em qualquer outro tipo de estrutura, deve-se procurar uma modulação econômica entre
os vãos de uma laje cogumelo protendida, Souza e Cunha [36]
apresentam a seguinte
recomendação:
• vão intermediários iguais entre si;
• vão extremos com comprimentos da ordem de 80 a 85% dos vão internos;
• balanços da ordem de 25 a 35% do vão adjacente, dependendo se há ou não
parede carregando a sua extremidade.
4.4. CONSUMO DE MATERIAIS
A titulo indicativo, para as condições médias de projeto, a referência [18] apresenta o seguinte
diagrama com os consumos de materiais:
Para lajes lisas com vãos entre 7 e 9 metros, para edifícios residenciais e comerciais, o
consumo de cordoalhas engraxadas gira em torno de 4 kg/m2
.
De acordo com Schmid [34]
, a viabilidade econômica para lajes cogumelo protendidas prende-se
fundamentalmente no parâmetro “vão”. Para vãos entre 7 e 10 metros, a solução com laje lisa
será naturalmente competitiva. Para vão maiores começam a se tornar interessantes outras
soluções como o uso de capitéis e lajes nervuradas.
Deve-se ressaltar que na avaliação econômicas das alternativas estruturais não se deve
comparar simplesmente o consumo dos materiais por metro quadrado. Mas sim o custo final,
onde se considera também o menor tempo de execução, o melhor reaproveitamento das
fôrmas e a própria aparência final da estrutura, por exemplo.
6 7 8 9 10 11 12
1
2
3
4
5
6
7
8
10
20
30
VÃO
(m)
CONSUMO
(kg/m²)
ESPESSURA
DA LAJE
(cm)
AÇO CP-190
(aderente)
CONCRETO
(fck = 25MPa)
CA-50
FAIXA ECONÔMICA
Figura 4.7: Gráfico de consumo de materiais para
lajes protendidas com cabos aderentes
Fonte: Ref. [18]](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-22-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 21
________________________________________________________________________________
Engº. Alexandre Emerick
4.5. DISTRIBUIÇÃO DOS CABOS EM PLANTA
Os esforços em um painel de laje cogumelo concentram-se com maior intensidade nas regiões
das faixas dos apoios. Dessa forma, é naturalmente recomendável que essas regiões
apresentem uma maior concentração de cabos. O ACI 423 [2]
apresenta a seguinte
recomendação para a distribuição dos cabos em planta:
• Faixa dos pilares: 65 a 75% dos cabos
• Faixa central: 35 a 25% dos cabos.
Figura 4.8: Distribuição dos cabos concentrando nas faixas dos pilares
De acordo com Souza e Cunha [36]
, as vantagens de usar cabos concentrados nas faixas dos
pilares, ao invés de uma distribuição uniforme são:
• uma melhor aproximação com a distribuição de momentos na laje;
• aumento da resistência à punção;
• aumento da resistência próximo ao pilar para a transferência de momentos de ligação
laje-pilar.
Entretanto, pode ser encontrada dificuldade para concentrar os cabos nas faixas dos pilares
devido às altas taxas de armadura existentes nestes. Contudo, deve ser adotado o mínimo de
2 cabos passando sobre os pilares.
Dependendo da situação pode-se buscar distribuições alternativas dos cabos como, por
exemplo, concentrar os cabos em faixas sobre os pilares em uma direção de distribuí-los na
outra, ou ainda a colocação de cabos apenas sobre as faixas dos pilares e armando com
ferragem passiva os painéis internos.
Em geral, no detalhamento de lajes cogumelo com protensão não-aderente, é comum o uso de
agrupamentos de cabos denominados feixes. O PR NB-1 indica que o número de cabos não-
aderentes dispostos em feixe deve ser de no máximo quatro, embora na prática sejam
encontrados feixes com até cinco cabos.
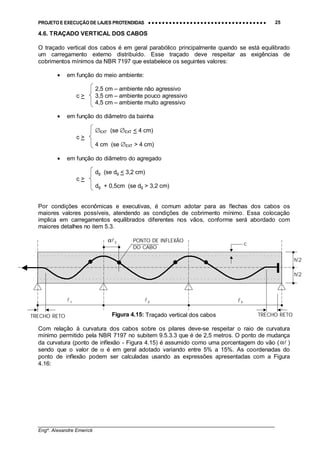
Segundo o PR NB-1, os cabos dispostos em faixas externas (faixa dos apoios) devem estar
contidos numa porção de laje, de tal forma que a largura desta não ultrapasse a dimensão em
planta do pilar de apoio, tomada transversalmente à direção longitudinal da faixa, acrescida de
3,5 vezes a espessura da laje, para cada um dos lados do pilar, conforme ilustra a Figura 4.9.
FAIXA CENTRAL
FAIXA DOS PILARES
FAIXA CENTRAL](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-23-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 22
________________________________________________________________________________
Engº. Alexandre Emerick
Vale ressaltar que quando se calcula os esforços na laje pelo processo do pórtico equivalente,
em geral adota-se a largura da faixa dos pilares como 25% ! , sendo ! dado de acordo com a
Figura 4.9, conforme indica a NB-1 [21]
. Ver mais detalhes no item 5.3.4 desse texto.
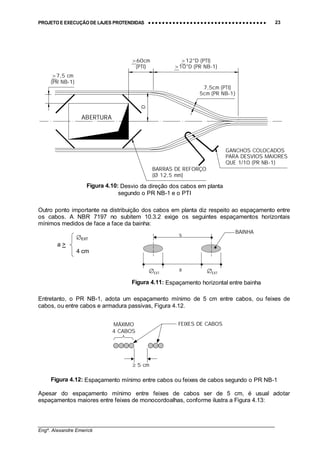
Quando existe a necessidade de fazer um desvio em planta do traçado dos cabos ou feixe de
cabos, o projeto de revisão da NB-1 prescreve que o desvio deve produzir uma inclinação
máxima de 1/10, na corda imaginária que une o início ao fim desse trecho, mantendo o seu
desenvolvimento de acordo com uma curva parabólica em planta. Ao longo do desvio o
conjunto de cabos ou feixes deve estar disposto de forma a manter uma distância de 5 cm
entre cabos na região central da curva. Quando os desvio dos cabos exceder a inclinação de
1/10 deve-se utilizar armadura capaz de absorver a força de desvio, Figura 4.10.
Segundo o projeto de revisão da NB-1, o cobrimento mínimo do cabo em relação à face de
aberturas nas lajes deve ser de 7,5 cm, conforme indicado na Figura 4.10.
O PTI [30]
também apresenta recomendações semelhantes às do PR NB-1 para desvios de
cabos. A Figura 4.10 apresenta as recomendações do PTI e do PR NB-1.
onde:
a – largura do pilar na direção
transversal à faixa;
A – largura da faixa para a distribuição
dos cabos;
h – espessura da laje;
! – vão entre apoios na direção
transversal à faixa.
Figura 4.9: Largura para a distribuição
de cabos nas faixas dos pilares
!
A ≤ a + 3,5h
FAIXACENTRAL
FAIXADOPILAR
a
FAIXADOPILAR](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-24-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 24
________________________________________________________________________________
Engº. Alexandre Emerick
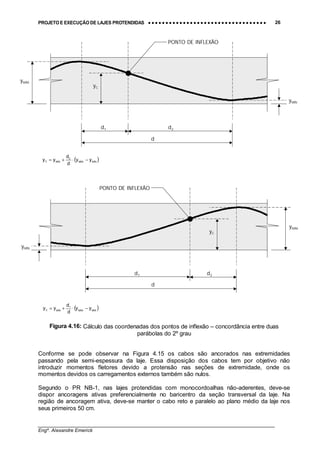
Figura 4.13: Espaçamento mínimo usual entre feixes de monocordoalhas
Na região próxima das ancoragens as cordoalhas agrupadas em feixes deverão ser
suavemente separadas, conforme ilustra a Figura 4.14.
FACE DA
FÔRMA
D
12*D MÍNIMO 90 cm
8cm8cm
3H/8
8cm
(MÍM)
FRETAGEM
Figura 4.14: Separação dos feixes de cabos na região das ancoragens
Fonte: PTI [30]
O espaçamento máximo dos cabos tem a função de garantir um comportamento adequado da
laje, com esforços bem distribuídos em toda a sua extensão. Usualmente adota-se como o
espaçamento máximo entre cabos o valor de 8d. Contudo, Park e Gamble [27]
recomendam que
esse espaçamento não exceda:
• s < 6h – para faixas centrais
• s < 4h – para as faixas dos pilares
sendo h a altura da laje.
Lin [15]
recomenda um espaçamento máximo fixo de:
• s < 135 cm – para lajes de cobertura
• s < 105 cm – para lajes dos demais pisos
Segundo o projeto de revisão da NB-1, o espaçamento entre cabos ou feixes de cabos deve
ser no máximo 6h, não excedendo 120 cm.
15 cm 20 cm
FEIXES DE 2 CABOS FEIXES DE 3 CABOS
25 cm
FEIXES DE 4 CABOS
S/ESC.](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-26-320.jpg)


![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 30
________________________________________________________________________________
Engº. Alexandre Emerick
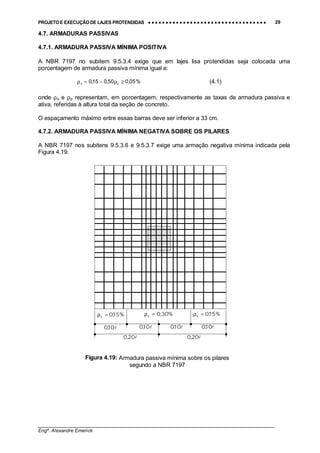
Com relação à distribuição da armadura passiva em lajes lisas e cogumelo, Fusco [13]
recomenda (Figura 4.20):
Figura 4.20: Distribuição da armadura passiva em lajes lisas e cogumelo
Fonte: Fusco [13]
4.7.3. ARMADURA DE REFORÇO DE BORDA DA LAJE
Nas bordas da laje é recomendável o uso de vigas. Essa recomendação torna-se ainda mais
necessária quando não há balanço, para se evitar problemas com punção dos pilares de canto
e extremidade. Entretanto, nem sempre é projetada essa viga de borda, nestes casos, deve-se
colocar uma armação passiva, como indicada na Figura 4.21, ao longo de todo o perímetro da
laje, conforme exige a NBR 7197 no subitem 9.5.3.7.
Figura 4.21: armadura de reforço de borda da laje
Lx
Ly
Ly/4
Ly/2
Ly/4(27,5%)
(27,5%)
(45%)
(37,5%)
(25%)
(37,5%)
(37,5%)
(25%)
(37,5%)
0,3Lx 0,3Lx 0,3Lx 0,3Lx
≥ 2h
∅10 ou ∅12.5 mm
corridos
∅6.3 ou ∅8mm
ESPAÇAMENTO ≤ h
h – ESPESSURA DA LAJE
AS BITOLAS INDICADAS SÃO APENAS
ILUSTRATIVAS, SENDO VÁLIDAS
SOMENTE PARA AS LAJES CORRENTES.](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-32-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 31
________________________________________________________________________________
Engº. Alexandre Emerick
4.7.4. ARMADURA CONTRA COLAPSO PROGRESSIVO
O projeto de revisão da NB-1 prevê no subitem 19.4.5 para lajes apoiadas diretamente sobre
pilares a colocação de uma armadura na região do pilar para combater o risco de colapso
progressivo. Entretanto, o subitem 20.4.2.6 prevê que se pode prescindir dessa armadura
quando pelo menos um cabo em cada direção ortogonal da laje, passar pelo interior da
armadura da armadura longitudinal contida na seção transversal do pilar ou elemento de apoio
em lajes de edifícios residenciais ou comerciais.
4.7.5. ARMADURA DE FRETAGEM
A armadura de fretagem tem por objetivo combater as tensões de tração introduzidas no
concreto devido à força de protensão. Essas tensões de tração surgem em decorrência da área
deduzida de contato entre a ancoragem e o concreto. Maiores detalhes sobre o cálculo dessas
tensões podem ser obtidos na Referência [13].
Na prática, para lajes com monocordoalhas engraxadas, recomenda-se adotar no mínimo as
seguintes armaduras de fretagem:
A) FRETAGEM PARA CONCENTRAÇÃO DE CABOS (FEIXES)
FACE DA
FÔRMA
> 8
> 8
> 8
> 25
N1
N2
3
4 N2 Ø10
N1
25
h-6
3h/8
15
N1 Ø10
h/2h/2
S/ ESC.
DIMENSÕES EM
CENTÍMETROS
Figura 4.22: Fretagem para feixes de cabos – ancoragem ativa – sistema com
monocordoalhas engraxadas](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-33-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 33
________________________________________________________________________________
Engº. Alexandre Emerick
BARRAS DE REFORÇO
2 N1 Ø12.5
S/ ESC.
DIMENSÕES EM
CENTÍMETROS
h/2h/2
SUPORTE
2 N1
FACE DA
FÔRMA
>30
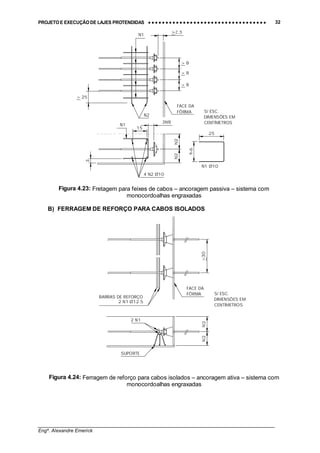
Figura 4.25: Ferragem de reforço para cabos isolados – ancoragem passiva – sistema com
monocordoalhas engraxadas
4.8. RECOMENDAÇÕES PARA EXECUÇÃO DE LAJES PROTENDIDAS
Nos próximos itens serão apresentadas algumas recomendações de procedimentos de campo
para a execução de lajes protendidas. Essas recomendações são baseadas nas referências
[14] e [7] direcionadas para o sistema não aderente com monocordoalhas engraxadas.
4.8.1. CONTROLE DE DOCUMENTOS
Certos documentos são fundamentais para o sucesso da execução de estruturas protendidas,
e devem estar à disposição do pessoal responsável pela execução e fiscalização da obra.
Estes documentos são:
a) Desenho de execução e detalhamentos (projetos).
b) Documentos com a especificação dos materiais usados.
c) Certificados dos materiais recebidos.
d) Certificado de calibragem do equipamento de protensão.
e) Tabelas de alongamentos obtidos com aprovação do engenheiro responsável, em geral,
o engenheiro projetista.
4.8.2. MANUSEIO E ARMAZENAMENTO
a) Durante o manuseio dos cabos deverão ser tomados cuidados para não danificar a
capa de plástico (PEAD) que envolve as cordoalhas, no caso da protensão não
aderente, ou amassar as bainhas metálicas para o sistema aderente.
b) A “fabricação” dos cabos, ou seja, o corte nos comprimentos do projeto e cravação das
ancoragens passivas (pré-blocagem), deverá ser feito em local abrigado e limpo.
Quando possível, deve-se evitar a “fabricação” no local da obra. A fabricação deve ser
supervisionada por pessoal habilitado. Para o serviço de pré-blocagem dos cabos deve
ser seguida a seguinte metodologia:](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-35-320.jpg)





![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 39
________________________________________________________________________________
Engº. Alexandre Emerick
4.8.7. ESCORAMENTOS
A Figura 4.28 mostra uma seqüência para a montagem e retirada do escoramento em lajes
protendidas. Em geral, recomenda-se que a concretagem dos pavimentos seja feita com pelo
menos dois ou três níveis de escoramento dependendo das dimensões das lajes.
As datas de aplicação da protensão são definidas pelos projetistas e estão vinculadas à
resistência do concreto na idade de protensão que deve ser comprovada previamente com
ensaios de corpos de prova.
Para as lajes usuais têm sido adotada protensão aos 4 dias podendo ser de todos os cabos ou
apenas uma parcela dependendo do projeto. Cabe ressaltar que o projeto deve apresentar, de
forma bastante clara, quais serão as idades de protensão, a resistência mínima do concreto e
os cabos que serão protendidos, caso a protensão seja feita em duas ou mais etapas. Deve ser
discutido com o projetista também o sistema de escoramento adotado, as datas para a retirada
das escoras, de preferência especificar o módulo de elasticidade mínimo do concreto e o
número de pavimentos que devem ser mantidos reescorados, além da forma como deve ser
feito o reescoramento.
Figura 4.28: Montagem e desmontagem do escoramento de lajes protendidas
Fonte: Ref. [18]
ESCORAMENTO EM
DESMONTAGEM
LAJE COM 100% DE
PROTENSÃO
LAJE COM 100% DE
PROTENSÃO (REESCORAMENTO)
LAJE COM 0 A 50% DE
PROTENSÃO
ESCORAMENTO EM
MONTAGEM
LAJE A CONCRETAR](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-41-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 40
________________________________________________________________________________
Engº. Alexandre Emerick
5. DIMENSIONAMENTO & VERIFICAÇÕES
Um dos métodos mais adequados para o cálculo de lajes protendidas é o método conhecido
como: “Método das Cargas Equilibrantes” (Load Balancing, Lin [15]
). Esse método consiste em
calcular qual a força de protensão necessária e o traçado dos cabos em elevação para
equilibrar uma determinada parcela do carregamento externo atuante. No item 5.3.3 será
apresenta uma análise um pouco mais detalhada sobre o Load Balancing.
No projeto de lajes protendidas a seqüência básica de cálculo é a seguinte:
#"Determinação da carga a ser equilibrada.
#"Fixação das excentricidades máximas dos cabos, função do cobrimento adotado.
#"Determinação da força de protensão necessária.
#"Cálculo da quantidade de cabos.
#"Verificação das tensões em serviço (Estados limites de serviço).
#"Verificação à ruptura.
5.1. DETERMINAÇÃO DA CARGA A SER EQUILIBRADA
Em geral adota-se o critério de que sobre a ação do carregamento quase permanente, a laje
não apresente flechas. Dessa forma, o carregamento de protensão deve equilibrar as cargas
permanentes e mais uma parcela das cargas de utilização.
O ACI Committee 423 [2]
apresenta o seguinte critério para lajes:
caso em que sejam previstas paredes divisórias leves e sobrecargas, num total de cerca de 2,0
a 3,0 kN/m2
(200 a 300 kgf/m2
): equilibrar o peso próprio + 0,5 kN/m2
(50 kgf/m2
);
caso em que sejam previstas paredes de alvenaria: equilibrar o peso próprio + 2/3 do peso das
paredes.
Outro critério bastante comum entre os projetistas é equilibrar o peso próprio mais 10% do
carregamento total.
5.2. FIXAÇÃO DAS EXCENTRICIDADES MÁXIMAS DO CABO
As excentricidades dos cabos devem respeitar as condições de cobrimento mínimo exigidos
pela NBR 7197, subitem 10.3.5, conforme discutido no item 4.6 desse trabalho. Maiores
detalhes sobre as implicações da escolha das excentricidades dos cabos são apresentados no
item 5.3.
5.3. DETERMINAÇÃO DA FORÇA DE PROTENSÃO NECESSÁRIA
Por hipótese, adota-se a força de protensão constante ao longo dos cabos, dessa forma, a
protensão necessária deve ser calculada para o vão mais desfavorável. Para as estruturas
usuais pode ser usada a formulação simplificada apresentada a seguir para o cálculo da força
de protensão:
1! 2! 3!
f1 f2
f3
q
Q
Figura 5.1: Cálculo da
protensão necessária](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-42-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 42
________________________________________________________________________________
Engº. Alexandre Emerick
Com relação à flecha dada aos cabos nos vãos podem ser adotados basicamente dois
procedimentos:
#"Adotar para o vão mais crítico um traçado que utiliza as excentricidades máximas (em
função do cobrimento mínimo), calcular a força de protensão necessária, e para os
demais vãos, calcular as excentricidades necessárias para obter o mesmo valor de
protensão.
#"Adotar para todos os vãos a excentricidade máxima e calcular a protensão para o vão
mais crítico.
A primeira possibilidade implica em um carregamento equilibrado constante em todos os vãos.
Contudo, alguns vãos podem ter um braço de alavanca reduzido, o que conduz a uma perda
de resistência da seção na ruptura.
A segunda possibilidade, que é a mais usual por aproveitar mais os cabos, implica em um
carregamento equilibrado diferente em cada vão. Esse fato não gera maiores problemas desde
que, calculados os esforços devido a esses carregamentos, as tensões em serviço obedeçam
aos limites apresentados no item 5.5.
Cabe, no entanto, ressaltar que principalmente em lajes com altura reduzida não faz sentido
variar muito a excentricidade dos cabos em cada vão, pois além de dificultar a execução, o que
se tem observado nas obras correntes, sobretudo residenciais e comerciais, que não existe um
controle rigoroso do posicionamento em elevação dos cabos, o que é agravado com o tráfego
de operários e equipamentos na laje no momento da colocação das armaduras passivas e da
concretagem.
Souza e Cunha [36]
, exemplificam que em uma laje com espessura de 22 cm, uma diferença
somente de 3 cm na colocação do cabo (em elevação) equivale a uma variação de cerca de
40% na excentricidade do cabo (a excentricidade varia de 8 para 5 cm). No entanto, a despeito
da constatação destes e de outros problemas em obras já executadas, em geral não
manifestam problemas estruturais, possivelmente porque as reservas de resistência destas
lajes são grandes.
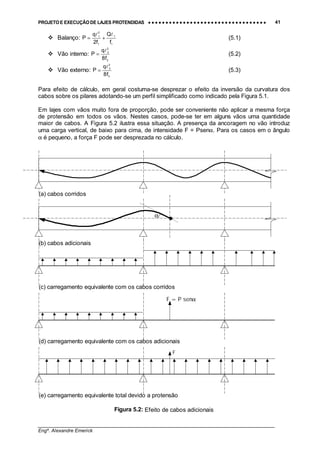
Quando se deseja equilibrar cargas concentradas nos vão internos o traçado mais adequado é
o apresentado na Figura 5.3, sendo a força de protensão dada pela equação 5.4.
Figura 5.3: Traçado do cabo para cargas concentradas
#"Carga concentrada:
f4
Q
P
!
= (5.4)
Caso seja necessário calcular a protensão para equilibrar um carregamento distribuído e uma
carga concentrada simultaneamente, pode usar o princípio da superposição e somar as
parcelas das equações 5.2 e 5.4.
Q
f
!](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-44-320.jpg)

![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 44
________________________________________________________________________________
Engº. Alexandre Emerick
5.3.2. CONSIDERAÇÃO DO EFEITO DA RIGIDEZ DOS PILARES
De acordo com Franco [11]
, contrariamente ao que acontece em geral nas obras de arte, onde a
mobilidade dos apoios é convenientemente assegurada por aparelhos especiais, nos edifícios
os elementos horizontais são geralmente ligados monoliticamente aos apoios, sejam eles
pilares ou muros. Devido a esse fato, parte da força de protensão é absorvido por esses apoios
reduzindo o esforço de compressão efetivamente atuante na laje (ou viga). Paralelamente a
essa perda, surgem esforços nos elementos de apoio.
É preciso portanto, cuidar, na fase de concepção do projeto, para que essa retenção seja a
menor possível, através de uma adequada disposição construtiva e de uma conveniente
dosagem das rigidezes dos elementos de suporte.
Uma avaliação simplificada desse efeito pode ser feita calculando um pórtico plano na direção
dos cabos colocando nas duas extremidades a força de protensão. Para exemplificar considere
a faixa de laje apresentada na Figura 5.6, com um total de 24 cabos protendidos com 14 tf (140
kN) cada e ainda admitindo que as perdas imediatas atinjam cerca de 6%:
Figura 5.6: Faixa de laje protendida
P = 24 × 14.000 × 0,94 = 315.840 kgf (3.158,4 kN)
A Figura 5.7 apresenta o pórtico plano com a carga P aplicada, enquanto que a Figura 5.8
apresenta o diagrama de esforços normais na laje. Observe que devido à rigidez dos pilares
ocorre uma redução de aproximadamente 5% na força de compressão atuante na laje, valor
esse que pode ser considerado durante o cálculo das perdas de protensão. A Figura 5.9
apresenta o diagrama de momentos fletores resultante. Observe que os pilares mais extremos
ficaram sujeitos a momentos fletores de cerca de 10,6 tf.m (106 kN.m) devido à força de
protensão. Esses momentos devem ser considerados no dimensionamento dos pilares,
cabendo, no entanto observar, que em determinados casos, a não consideração desses
momentos nos pilares pode estar a favor da segurança (é o caso dos pilares abaixo da laje
onde os momentos estão em sentido contrário aos momentos que surgirão devidos aos
carregamentos externos como, por exemplo, a sobrecarga).
80 80 80 80
20 20 20 20
200 200800 800 800
CP 190 RB – 24 ∅ 12,7mm (14 tf /cabo)
800
Espessura = 20
Dimensões em cm](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-46-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 45
________________________________________________________________________________
Engº. Alexandre Emerick
Unidade: kgf
Figura 5.7: Modelo estrutural adotado – pórtico plano com a carga devido a protensão
Unidade: kgf
Figura 5.8: Diagrama de esforços de compressão na laje
Unidade: tf.m
Figura 5.9: Diagrama de momentos fletores
Com relação ao efeito da protensão nas cargas verticais dos pilares, segundo Campos [6]
, para
estruturas convencionais com lajes lisas ou nervuradas protendidas, a protensão tende a
apresentar um acréscimo de cerca de 10% nas cargas finais que chegam às fundações.
5.3.3. CONSIDERAÇÃO DO EFEITO DA INVERSÃO DE CURVATURA NO PERFIL DOS
CABOS SOBRE OS PILARES
Conforme mencionado anteriormente, para o cálculo de lajes protendidas é comum desprezar
o efeito da inversão da curvatura dos cabos sobre os pilares. Entretanto, para cálculos que
exijam maior precisão, esse efeito pode ser avaliado usando a formulação apresentada por
Naaman [20]
e descrita a seguir:
5.3.3.1. VÃOS DE EXTREMIDADE
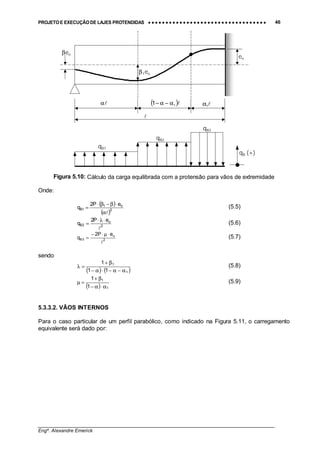
Para o caso particular de um perfil parabólico, como indicado na Figura 5.10, o carregamento
equivalente será dado por:](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-47-320.jpg)

![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 48
________________________________________________________________________________
Engº. Alexandre Emerick
Figura 5.12: Cálculo da carga equilibrada com a protensão para balanços
( ) 2
3
1
1B
1
Pe2
q
!α−
≅ (5.12)
2
3
o
2B
)(
Pe2
q
!α
−
= (5.13)
sendo,
( ) 031 e1e ⋅α−≅ (5.14)
onde α3 = 0,05 a 0,20 dependendo do vão do balanço.
5.3.4. ENGASTAMENTO NOS PILARES
De acordo com Franco [11]
, é vantajoso nas estruturas de edifícios engastar as extremidades
das vigas em seus respectivos pilares, mobilizando assim um benéfico efeito de pórtico. Neste
caso, o cabo resultante deverá ser ancorado excentricamente, e introduzirá na estrutura um
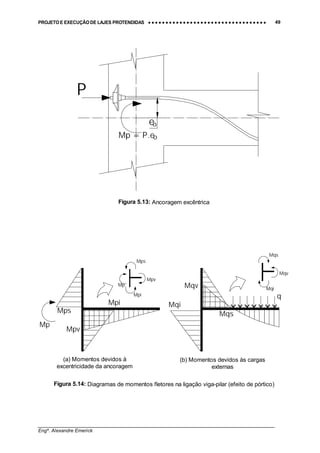
momento primário, Mp = P⋅ eo, Figura 5.13, que será por sua vez distribuído parte para o pilar e
parte para a viga. Se o pilar tiver rigidez grande com relação à viga, ele reterá grande parte
daquele momento, reduzindo os esforços solicitantes e as deformações desta última.
Conforme ilustra a Figura 5.14, os momentos resultantes da excentricidade da protensão tende
a equilibrar, em parte, os momentos provenientes do carregamento externo.
eo
( )!31 α− !3α
!
e1
qB1
qB2
qB (+)](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-50-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 50
________________________________________________________________________________
Engº. Alexandre Emerick
CABOS
B
P
AV
A C D
5.3.5. MÉTODO DAS CARGAS EQUILIBRANTES – LOAD BALANCING
O Método das cargas equilibrantes, Lin [15]
, é um dos métodos mais apropriados para o cálculo
de lajes protendidas. Conforme mencionado anteriormente, o método consiste em calcular qual
a força de protensão necessária e o traçado dos cabos em elevação para equilibrar uma
determinada parcela do carregamento externo atuante. Os esforços obtidos a partir da carga
balanceada são compostos de duas parcelas: a primeira referente ao efeito isostático da
protensão e a segunda referente ao efeito hiperestático.
A) EFEITO ISOSTÁTICO (MOMENTO PRIMÁRIO)
Seja a viga protendida com três vãos apresentada na Figura 5.15. A Figura 5.16a e 5.16b
apresentam os esquemas de forças na viga e no cabo devido ao efeito da protensão.
Figura 5.15: Viga protendida com três vãos
Figura 5.16: Esquema de forças para a viga e o cabo
(a) Esquema de forças na viga
devido ao efeito da protensão
(b) Esquema de forças no cabo
devido ao efeito da protensão
A B C D
VA
VD
P P
P P
VA VD
q(x)
q(x)
a
S
S](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-52-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 51
________________________________________________________________________________
Engº. Alexandre Emerick
Considera uma seção S posicionada a uma distância “a” da ancoragem. O momento MISO,
Figura 5.17, necessário para manter o equilíbrio é denominado momento isostático, ou
momento primário e é dado pela expressão (5.15).
( )[ ]∫ += aVxdxxqM AISO (5.15)
Onde, MISO – momento isostático;
q(x) – intensidade da carga balanceada na abscissa x;
VA – componente vertical da força de protensão aplicada na ancoragem;
a – distância da seção S à face da viga.
x
VA
a
P
A
q(x)
SB
dx
P
ISOM
Vx
Considerando agora o esquema de forças para o cabo na mesma seção S, Figura 5.18, obtém-
se:
Figura 5.17: Esquema de força na viga – Seção S
Figura 5.18: Esquema de força no cabo – Seção S
VA
VX
e
q(x)
S
xdx
a
P
P](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-53-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 52
________________________________________________________________________________
Engº. Alexandre Emerick
A
MHIP
d
(+)
Rj
B C D
( )[ ]∫ +⋅=⋅ aVxdxxqeP A (5.16)
Comparando as expressões (5.15) e (5.16) observa-se que:
ePMISO ⋅= (5.17)
Observe que a definição do momento isostático, conforme foi ilustrado, é independente das
condições de apoio da viga e as cargas balanceadas.
B) EFEITO HIPERESTÁTICO (MOMENTO SECUNDÁRIO)
Considere a mesma viga protendida da Figura 5.15 e imagine que os dois apoios
intermediários fossem retirados, Figura 5.19a. Após a protensão dos cabos a viga apresenta
um deslocamento vertical para cima, Figura 5.19b. Entretanto, devido à existência dos apoios
intermediários ela não poderá se deslocar surgindo as reações indicadas na Figura 5.19c,
chamadas de reações hiperestáticas ou secundárias. Essas reações geram o diagrama de
momentos fletores da Figura 5.19d.
Figura 5.19: Efeito hiperestático de protensão
Nas estruturas hiperestáticas, a continuidade da estrutura se opõe à livre deformação de cada
tramo, sob efeito das solicitações de protensão, dando origem a momentos fletores e esforços
cortantes. Esse fato é denominado efeito hiperestático de protensão.
As reações da Figura 5.19c são provenientes apenas da protensão, como elas são as únicas
forças na viga, elas devem ser alto equilibradas. Dessa forma:
∑ = 0Rj (5.18)
A partir do esquema de forças na seção S da viga, Figura 5.20, tem-se que:
(a) Viga da Figura 5.15
retirando-se os apoios
intermediários
(b) deslocamento gerado
pelo efeito da protensão
(c) reações devido às
restrições dos apoios
intermediários
(d) diagrama de
momentos fletores
resultante](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-54-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 53
________________________________________________________________________________
Engº. Alexandre Emerick
∑ == 0xRM jjHIP (5.19)
∑ == 0RV jHIP (5.20)
BA
jx
S
a
jR
HIPV
HIPM
Onde,
MHIP – momento hiperestático de protensão;
VHIP – esforço cortante hiperestático de protensão;
Rj – reação devido ao efeito hiperestático de protensão.
Segundo Pfeil [28]
, no que diz respeito à redistribuição dos momentos hiperestáticos, decorrente
da inelasticidade da estrutura, é muito mais complexa que a redistribuição dos esforços
provocados pelas cargas atuantes. Três são os principais fatores influentes no fenômeno:
#"As reduções locais de rigidez, nas seções fissuradas, produzem uma redistribuição dos
efeitos hiperestáticos de protensão.
#"A plastificação da estrutura diminui o grau de hiperestaticidade, o que provoca uma
redução nos valores dos momentos hiperestáticos de protensão.
#"Com o aumento das solicitações atuantes, o esforço de protensão sofre um aumento
nas seções fissuras, porém mantém-se aproximadamente inalterado na maior parte do
comprimento da viga.
Com os conhecimentos disponíveis atualmente, não é possível dizer com precisão qual a
influencia da inelasticidade da estrutura sobre o momento hiperestático de protensão, nos
estágios de carregamento próximo à ruptura. Nessas condições, é usual considerar o momento
hiperestático de protensão calculado com o valor da protensão efetiva, como uma solicitação
que soma aos momentos solicitantes de projeto produzidos pelos carregamentos.
Figura 5.20: Esquema de forças na viga devido ao efeito
hiperestático – Seção S](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-55-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 54
________________________________________________________________________________
Engº. Alexandre Emerick
C) MOMENTO BALANCEADO
A Figura 5.21 apresenta o esquema de forças na seção S para viga considerando a
combinação do efeito isostático e o efeito hiperestático.
B
x
A
xj
S
a
MBAL
P
BALV
AV
P
q(x)
dx
Rj
Para o equilíbrio da seção tem-se que:
( )[ ] ∑∫ ++⋅= jjABAL xRaVxdxxqM (5.21)
Logo,
HIPISOBAL MMM += (5.22)
onde,
MBAL – momento balanceado com a protensão.
Portanto, os esforços obtidos com o método das cargas equilibrantes incluem o efeito isostático
e o efeito hiperestático, conforme afirmado anteriormente. Dessa forma, para a obtenção dos
esforços devidos ao efeito hiperestático pode-se adotar o seguinte procedimento: calculam-se
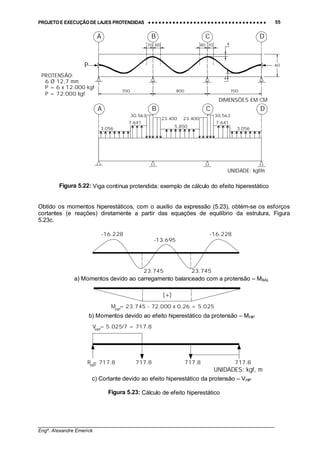
os esforços gerados pela carga equilibrada com a protensão. Sobre os apoios o momento
hiperestático será dado pela expressão (5.23), na região entre apoios os momentos poderão
ser obtidos por interpolação linear, conforme ilustra o exemplo da Figura 5.22.
PeMM BALHIP += (5.23)
Figura 5.21: Esquema de forças na viga
(efeito isostático + hiperestático) – Seção S](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-56-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 56
________________________________________________________________________________
Engº. Alexandre Emerick
O procedimento apresentado para o cálculo dos momentos hiperestáticos é valido para o caso
de vigas contínuas, podendo ser estendido para lajes quando o cálculo é feito como faixas ou
pórticos equivalentes. Para lajes com distribuição de cabos e geometria irregular a
determinação do efeito hiperestático é bem mais complexa, sendo necessário recorrer a
procedimentos numéricos. Entretanto, como o efeito hiperestático é um redistribuidor de
esforços pode-se suprir em parte a falha na sua avaliação fazendo uma redistribuição nos
momentos negativos da ordem de 20% (15% de plastificação e 5% de efeito hiperestático),
aumentando-se os momentos positivos na mesma proporção.
5.3.6. CALCULO DE LAJES LISAS E COGUMELO PELO MÉTODO DO PÓRTICO
EQUIVALENTE
Para o cálculo de lajes lisas e cogumelo podem ser usados diversos processos, tais como:
#"método dos pórticos equivalentes (pórtico da NB-1);
#"cálculo como viga contínua;
#"método dos pórticos equivalentes (pórtico do ACI 318 [1]
);
#"método empírico (ACI, válido em determinadas condições);
#"tabelas para cálculo de esforços e flechas em lajes cogumelo publicadas pelo CEB [9]
.
#"linhas de ruptura;
#"métodos numéricos como grelhas e método dos elementos finitos.
O cálculo de lajes lisas e cogumelo pelo processo dos pórticos equivalentes tem sido
largamente utilizado. O ACI [1]
permite o cálculo como pórticos para estruturas com pilares que
apresentem no máximo um desvio de 10% em relação ao alinhamento dos demais, limitação
que também está presente no PR NB-1. Evidentemente para lajes bastante irregulares, com
pilares desalinhados, presença de grandes aberturas é recomendável o uso de métodos mais
refinados como o método das grelhas ou o método dos elementos finitos.
Segundo Franco [11]
, a disponibilidade de diversos programas de elementos finitos permite
efetuar, a baixo custo, uma análise mais rigorosa da laje. A discretização deverá ser
necessariamente densa na região próxima aos pilares, sendo possível considerar uma
plastificação dos elementos situados nas regiões mais solicitadas através de uma adequada
redução de seu módulo de elasticidade. A influência da protensão é facilmente levada em
conta usando o método das cargas equilibrantes.
5.3.6.1. MÉTODO DO PÓRTICO EQUIVALENTE – SEGUNDO A NB-1
A NB-1/78 (NBR 6118) subitem 3.3.2.11 prescreve que:
As lajes apoiadas diretamente sobre pilares serão calculadas em regime elástico ou rígido
plástico de acordo com os subitens 3.3.2.1 e 3.3.2.2.
Quando os pilares estiverem dispostos em filas ortogonais e a espessura da laje respeitar o
mínimo do subitem 6.1.1.1, será permitido calcular em regime elástico o conjunto lajes-pilares
como pórticos múltiplos, admitindo-se a laje dividida em duas séries ortogonais de vigas e
considerando-se no cálculo de cada série o total das cargas. A distribuição dos momentos, se
dividirem os painéis das lajes, com os cantos correspondendo aos pilares, em quatro faixas
iguais, será feita do seguinte modo:
#"45% dos momentos positivos para as duas faixas internas;
#"27,5% dos momentos positivos para cada uma das faixas externas;
#"25% dos momentos negativos para as duas faixas internas;
#"37,5% dos momentos negativos para cada uma das faixas externas.](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-58-320.jpg)

![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 58
________________________________________________________________________________
Engº. Alexandre Emerick
A Figura 5.25 mostra os pórticos da direção X para a laje em questão. De forma análoga serão
obtidos os pórticos na direção Y. Os pórticos obtidos nas duas direções deverão ser calculados
independentemente uns dos outros.
O leitor deve observar que no cálculo do pórtico equivalente considera-se a totalidade das
cargas em ambas as direções. Segundo Fusco [13]
, esse fato não é um exagero e pode ser
explicado com um exemplo simples: Na Figura 5.26 observe que o transporte de uma carga F
de seu ponto de aplicação até um pilar corresponde a um momento F⋅a, que pode ser
decomposto nas componentes F⋅ax e F⋅ay, para as quais, em ambos os casos, a força F entra
com o total de sua intensidade.
Figura 5.26: Transferência de uma carga F para o pilar
Entretanto, com relação à reação vertical em cada pilar, em geral adota-se a maior reação
obtida considerando o pórtico na direção X e na direção Y, não devendo somar as duas
reações.
Segundo Fusco [13]
, quando os momentos na laje são obtidos através do cálculo de pórtico, não
se deve fazer o “arredondamento” dos momentos negativos, devendo ser adotado no momento
máximo, Figura 5.27.
a
ay
F
ax
Figura 5.27: Consideração integral dos momentos
negativos sobre os apoios
MAPOIO
MAPOIO
NÃO ARREDONDAR MAPOIO
MVÃO](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-60-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 59
________________________________________________________________________________
Engº. Alexandre Emerick
A Figura 5.28 apresenta a distribuição dos momentos nas faixas de acordo com a NB-1.
5.3.6.2. MÉTODO DO PÓRTICO EQUIVALENTE – SEGUNDO O ACI 318
O método do pórtico equivalente segundo o ACI-318/95 [1]
apresenta algumas diferenciações
com relação ao pórtico da NB-1/78.
A primeira diz respeito à definição das faixas para distribuição dos momentos, o ACI considera
a largura das faixas definidas por 25% do menor vão da laje, Figura 5.29, enquanto a NB-1
adota 25% do vão na direção do pórtico.
MAPOIO
MVÃO
MAPOIO
x5,0 !⋅x25,0 !⋅ x25,0 !⋅
M1M1
M2
M3 M3
M4
MOMENTOS NAS FAIXAS:
x
APOIO
1
25,0
M
375,0M
!
=
x
VÃO
3
25,0
M
275,0M
!
=
x
APOIO
2
5,0
M
25,0M
!
=
x
VÃO
4
5,0
M
45,0M
!
=
RESULTADO DO PÓRTICO
EQUIVALENTE
Figura 5.28: Distribuição dos momentos nas
faixas segundo a NB-1
DISTRIBUIÇÃO
REAL DOS
MOMENTOS
DISTRIBUIÇÃO
IDEALIZADA](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-61-320.jpg)




![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 64
________________________________________________________________________________
Engº. Alexandre Emerick
onde:
fptk é a tensão característica de ruptura do aço;
fpyk é a tensão característica de escoamento (convencional) do aço.
Entretanto, o projeto de revisão da NB-1 modifica um pouco esses valores adotando:
#"Aços de relaxação normal:
0,74 fptk
σpi <
0,87 fpyk
#"Aços de relaxação baixa:
0,74 fptk
σpi <
0,82 fpyk
Considerando o limite do PR NB-1, que é mais conservador, pode-se adotar para a cordoalha
de ∅12,7 mm com aço CP190 RB uma força de protensão inicial de 14 tf (140 kN), e para a
cordoalha de ∅15,2 mm uma protensão inicial de 19,7 tf (197 kN). Entretanto, na prática os
valores adotados de protensão inicial tem sido: 15 tf (150 kN) para a cordoalha de ∅12,7 mm e
20 tf (200 kN) para a cordoalha de ∅15,2 mm.
5.5. VERIFICAÇÃO DAS TENSÕES EM SERVIÇO
O ACI Committee 423 [2]
recomenda limites para tensão admissível em membros fletidos de
concreto protendido. De acordo com o ACI:
Para laje com protensão não aderente a tensão média de compressão na laje deve estar no
intervalo entre 0,86 MPa e 3,5 MPa.
#"Tensões no concreto imediatamente após a aplicação da protensão, em MPa:
(a) compressão na zona de momento negativo ..................... ci'f40,0 ⋅
(b) compressão na zona de momento positivo ...................... ci'f60,0 ⋅
(c) tração (com armadura passiva) ........................................ ci'f50,0
NOTA:
Onde a tensão de tração no concreto exceder os valores acima, uma armadura auxiliar
aderente (passiva ou ativa) deverá ser colocada para resistir à tensão total de tração.
#"Tensões no concreto em serviço (após as perdas no tempo), em MPa:
(a) compressão na zona de momento negativo ..................... c'f30,0 ⋅
(b) compressão na zona de momento positivo ...................... c'f45,0 ⋅
(c) tração (com armadura passiva) ........................................ c'f50,0
onde,
f’c é a resistência à compressão do concreto especificada;
f’ci é a resistência à compressão do concreto na idade “i” dias;](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-66-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 65
________________________________________________________________________________
Engº. Alexandre Emerick
Simplificadamente pode-se assumir que f’c seja igual ao fck.
A NBR 7197 exige:
#"(item 4.1.3.a) Para a protensão parcial quando atuando a combinação quase
permanente das ações previstas no projeto, deve ser respeitado o Estado Limite de
Descompressão (6.2.1);
#"(item 4.1.3.b) Para a protensão parcial quando atuando a combinação freqüente das
ações previstas no projeto deve ser respeitado o limite para abertura de fissuras (6.2.3)
wk < 0,2 mm;
#"(item 6.2.5) No ato da protensão seja respeitado o Estado Limite de Compressão
Excessiva que corresponde a limitar as tensões a 0,70 fck,j;
Onde fck,j é a resistência característica do concreto na idade j dias, sendo j a idade de
protensão.
A valor de fck,j pode ser obtido pela expressão 5.29 extraída do PR NB-1:
ck1j,ck ff β= (5.29)
com,
−=β
2
1
1
j
28
1sexp , com s igual a:
s TIPO DE CIMENTO
0,20 CPV
0,25 CPI, CPII
0,38 CPIII e CPIV
O valor do fck,j adotado na idade de protensão deve sempre constar nas folhas do projeto.
Com relação ao item 4.1.3a da NBR 7197 vale ressaltar que o projeto de revisão da NB-1 [22]
no
item 8.1.6 apresenta como limite para o uso da protensão parcial que para a combinação
quase permanente das ações seja respeitado o Estado Limite de Formação de Fissuras (ELS-
F), sendo portanto, menos rigorosa que a NBR 7197, pois admite um pequeno nível de tração
no concreto.
Conforme o projeto de revisão da NB-1 o ELS-F é atingido quando a máxima tensão de tração
na seção de concreto atinge o limite fctk, onde:
32
ckinf,ctkctk f21,0ff ⋅== (MPa) (5.30)
A Tabela 5.1 apresenta os valores de resistência à tração do concreto segundo o PR NB-1.
Tabela 5.1: Resistência à tração do concreto segundo o PR NB-1
fck (MPa) fctk,inf (MPa)
25 1,80
30 2,03
35 2,25
40 2,46
45 2,66
50 2,85
O Estado limite de fissuração inaceitável pode ser verificado avaliando a abertura das fissuras
segundo o critério adotado pela NB-1 [21]
e pela NBR 7197 [23]
. A seguir é apresentado um](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-67-320.jpg)



![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 69
________________________________________________________________________________
Engº. Alexandre Emerick
3
2
ckm,ct f3,0f ⋅= , em MPa, ou (5.44a)
3
2
ckm,ct f646,0f ⋅= , em kgf/cm2
(5.44b)
5.6. VERIFICAÇÃO À RUPTURA POR FLEXÃO – ESTADO LIMITE ÚLTIMO
O estado limite último, Estádio III, corresponde a uma condição em que a estrutura não pode
ser mais utilizada, por ter sofrido colapso ou deformações plásticas excessivas. O cálculo no
estado limite último por flexão pode ser feito considerando as seguintes hipóteses:
#"As deformações das fibras são proporcionais à sua distância ao eixo neutro, ou seja, as
seções planas permanecem planas até a ruptura.
#"A intensidade e a posição da resultante dos esforços que atuam na região comprimida
do concreto podem ser deduzidas de um diagrama de tensões simplificado. Os
diagramas mais utilizados são o parábola-retângulo e o retangular equivalente.
#"Após a fissuração, a resistência à tração do concreto é totalmente desprezada.
#"Sob influência das solicitações, as armaduras ficam sujeitas às mesmas deformações
unitárias médias que o concreto adjacente.
Para as armaduras passivas as tensões são obtidas diretamente do diagrama tensão-
deformação correspondente do aço.
Para as armaduras protendidas aderentes, deve-se considerar além da deformação devido à
curvatura do concreto, o pré-alongamento aplicado devido a protensão.
Para armaduras não aderentes deve-se considerar também o pré-alongamento do aço devido
a protensão. Entretanto, o cabo não aderente não acompanha o alongamento unitário do
concreto, de modo que a tensão σpd, no estado limite, é inferior à que seria obtida no caso do
cabo aderente. Assim, a contribuição do cabo não aderente, para o momento resistente é
inferior à do cabo aderente.
De acordo com a NB-1/78 o estado limite último por flexão é caracterizado pelos seguintes
valores de deformações unitárias:
εcu = 3,5 o
/oo – encurtamento máximo do concreto
εsu = 10 o
/oo – deformação plástica excessiva da armadura.
De acordo com Veríssimo et al [36]
, o limite convencional de 10o
/oo para a deformação no aço
está relacionado à fissuração do concreto. Quando a deformação na armadura mais tracionada
atinge um valor tão elevado, o concreto adjacente encontra-se fissurado e com abertura de
fissuras muito grandes. Numa peça com fissuras espaçadas de 10 cm, por exemplo, uma
deformação de 10o
/oo acarreta em fissuras da ordem de 1 mm.
Cabe observar que nas armaduras protendidas o alongamento máximo é contado a partir do
estado de descompressão da seção, que é uma situação fictícia onde a protensão equilibra
uma parcela de carga externa tal que anule todas as tensões na seção transversal de concreto.
A máxima a tensão atingida pelo concreto será de: σcd = 0,85 fcd
Com relação à verificação do E.L.U. o NBR 7197 prescreve que devem ser considerados, além
do efeito de outras ações, apenas os esforços solicitantes hiperestáticos de protensão. O efeito
isostático de protensão não deve ser incluído. Isso ocorre pois a protensão é considerada uma
solicitação interna, ficando normalmente a seção submetida à flexão simples. A consideração
das armaduras ativas nos esforços resistentes deve ser feita a partir dos diagramas tensão-
deformação e da consideração do pré-alongamentos das mesmas. Esses pré-alongamentos](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-71-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 70
________________________________________________________________________________
Engº. Alexandre Emerick
devem calculados com base nas tensões iniciais de protensão com valores de cálculo e com a
consideração de perdas na idade t em exame.
Veríssimo et al [36]
apresenta o seguinte procedimento para o cálculo da capacidade resistente
de uma seção de concreto protendido ao momento fletor:
#"Determina-se o valor de cálculo da força de protensão.
#"Calcula-se o pré-alongamento da armadura ativa.
#"Determina-se o alongamento e a respectiva tensão no aço de protensão, em função da
rotação da seção provocada pelo momento fletor. No caso de cabos aderentes, a
determinação desse alongamento é feita com base na hipótese de aderência perfeita
entre aço e concreto. Entretanto, no caso de cabos não aderentes, a análise pode ser
feita de forma aproximada levando em conta um coeficiente de aderência, entre o cabo
e a laje, o qual pode variar entre 0 (cabo idealmente não aderente) e 1 (cabo aderente).
#"Verifica-se o equilíbrio da seção. Caso a força de tração na armadura ativa seja menor
que a força menor que a força de compressão no concreto, deve ser acrescentada uma
armadura passiva complementar. Caso a força de traça na armadura ativa seja maior
ou igual á força de compressão no concreto, a armadura é suficiente para suportar o
carregamento atuante. Neste caso, deve-se colocar a armadura passiva mínima
recomendada pela norma.
A Figura 5.37 apresenta o esquema de forças em uma seção no Estádio III considerando o
diagrama retangular equivalente de tensões no concreto.
Figura 5.37: Seção de concreto protendido no Estádio III
Equações de equilíbrio da seção:
∑ = 0FH stptcc RRR += (5.45)
∑ = 0M 2st1ccd ZRZRM += (5.46)
DETERMINAÇÃO DO VALOR DE CÁLCULO DA FORÇA DE PROTENSÃO
Para o cálculo do pré-alongamento da armadura protendida, deve-se conhecer o valor de
cálculo da força de protensão:
y=0,8x
0,85 fcd
Rcc
Rpt = AP σpd
Rst = As σsd
dp
ds
εp
εc
εs
Md
x
Z1
Z2
LN](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-72-320.jpg)


![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 73
________________________________________________________________________________
Engº. Alexandre Emerick
Obtida a deformação εp devido à curvatura da seção, calcula-se a deformação total, εpt,
acrescentando-se o pré-alongamento, εpn.
pnppt ε+ε=ε (5.54)
A deformação de cálculo será:
s
pt
pd
γ
ε
=ε , com 15,1s =γ (5.55)
Figura 5.39: Diagrama tensão-deformação para aço CP-175 e CP-190
Fonte: Schmid [34]
Observe que entrando com o valor de cálculo da deformação, εpd, na curva da Figura 5.39, a
tensão calculada será a tensão de cálculo, σpd.
EXEMPLO – PROTENSÃO ADERENTE
Para ilustrar o procedimento de verificação à ruptura por flexão em uma laje com protensão
aderente, considere a seguinte situação hipotética:
Figura 5.40: Laje com protensão aderente - exemplo
5,11
7,70
9,00
50,0
0,61
0,76
0,78
0,87
ptk
p
f
σ
εp (o
/oo)O
A
B
C
D
TRECHO AO: p
ptk
p
1130,0
f
ε=
σ
TRECHO AB: 592,0328,00198,0
f
p
2
p
ptk
p
−ε⋅+ε⋅−=
σ
(AÇO CP 175)
324,0218,00097,0
f
p
2
p
ptk
p
−ε⋅+ε⋅−=
σ
(AÇO CP 190)
TRECHO BC: 642,0
65
1
f
p
ptk
p
+ε⋅=
σ
TRECHO CD: 760,0
456
1
f
p
ptk
p
+ε⋅=
σ
4
2 ∅ 12,7
50 50
21
25](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-75-320.jpg)

![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 75
________________________________________________________________________________
Engº. Alexandre Emerick
69,1437,632,8pnppt =+=ε+ε=ε o
/oo
A partir do gráfico da Figura 5.39 obtém-se a tensão na armadura protendida:
792,0760,069,14
456
1
fptk
p
=+⋅=
σ
( )MPa503.1
cm
kgf030.15
987,0
730.18
792,0f792,0 2ptkp =⋅=⋅=σ
Tensão de cálculo: ( )MPa307.1
cm
kgf6,069.13
15,1
030.15
2
s
p
pd ==
γ
σ
=σ
Calculando a resultante de compressão no concreto obtém-se:
( )kN6,983kgf357.98
4,1
300
85,010075,68,0f85,0bx8,0R cdcc =⋅⋅⋅=⋅⋅=
A resultante de tração na armadura protendida será:
( )kN3,516kgf625.5195,36,069.13AR ppdpt =⋅=⋅σ=
Como Rpt < Rcc a seção não está em equilíbrio. É necessário adicionar armadura passiva de tal
forma que:
( )kN3,467kgf732.46625.51357.98RRR ptccst =−=−=
A armadura passiva necessária será:
m
cm75,10
348.4
732.46
f
R
A
2
yd
st
s === $ ∅12,5 c/ 11cm
B) ARMADURA NÃO ADERENTE
Para o cálculo da tensão no aço protendido, σpd, no caso de monocordoalhas engraxadas é
usual recorrer a fórmulas empíricas, como as apresentadas a seguir que são baseadas no ACI-
318 [1]
:
a) para peças com relação vão-espessura L/h ≤ 35:
pykpe
p
ck
pnp f420
100
f
70 ≤+σ≤
ρ
++σ=σ (MPa) (5.56)
b) para peças com relação vão-espessura L/h > 35:
pykpe
p
ck
pnp f200
300
f
70 ≤+σ≤
ρ
++σ=σ (MPa) (5.57)
As expressões (5.56) e (5.57) são válidas para ptkpe f5,0≥σ .
A tensão de cálculo será:
s
p
pd
γ
σ
=σ , com sγ =1,15 (5.58)
onde:
pnσ – tensão na armadura protendida devido ao pré-alongamento. Obtida a partir do
diagrama tensão-deformação do aço (Figura 5.39) para εpn dado pela expressão (5.50);](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-77-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 77
________________________________________________________________________________
Engº. Alexandre Emerick
( )kN1,476kgf3,615.477,741.50357.98RRR ptccst =−=−=
A armadura passiva necessária será:
m
cm95,10
348.4
3,615.47
f
R
A
2
yd
st
s === $ ∅12,5 c/ 11cm
5.6.1. VERIFICAÇÃO À RUPTURA POR FLEXÃO – FÓRMULAS APROXIMADAS
Atualmente, com a disponibilidade de programas computacionais, a verificação de seções de
concreto protendido deixou de ser uma tarefa trabalhosa para o projetista. Contudo, ainda hoje
são de grande valia as formulações simplificadas, pois permitem ao projetista que faça cálculos
rápidos bastante úteis em pré-dimensionamentos e verificações.
A seguir são apresentadas fórmulas aproximadas obtidas através de pesquisas experimentais
e cálculos numéricos comparativos para a verificação do momento resistente de uma seção em
concreto protendido. Essas fórmulas foram extraídas da referência [28] e são baseadas nos
trabalhos de Lin [15]
.
A) SEÇÃO RETANGULAR
Para uma seção subarmada, o braço de alavanca interno, Z, pode ser obtido pela seguinte
expressão empírica.
( )p6,01dZ ω−⋅= (5.59)
onde,
d – altura útil. O valor de d é estimado considerando a posição da resultante dos
esforços de tração:
ydspdp
sydsppdp
fAA
dfAdA
d
+σ
+σ
= (5.60)
ωp – taxa mecânica de armadura protendida.
cd
pd
pp
σ
σ
ρ=ω (5.61)
O momento resistente da seção será dado pela expressão (5.62):
( ) ( )pydspdpdR 6,01dfAAM ω−⋅⋅+σ= (5.62)
Impondo uma condição de ductilidade de obter um alongamento mínimo de 0,5% nas
armaduras, obtém-se o seguinte limite pra o momento resistente:
cd
2
LIM,dRdR bd28,0MM σ⋅=≤ (5.63)
Considerando:
b = 1 metro,
γc = 1,4
Efeito Rüsch = 0,85
O valor de MdR,LIM pode ser obtido pela expressão (5.64) adotando os valores de κ1 da Tabela
5.2.](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-79-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 78
________________________________________________________________________________
Engº. Alexandre Emerick
2
1LIM,dR dM ⋅κ= (5.64)
Tabela 5.2: Valores de κ1 para o cálculo de MdR,LIM
fck fck κκκκ1
(MPa) (kgf/cm²) (kgf.m/cm²)
20 200 34,0
25 250 42,5
30 300 51,0
35 350 59,5
40 400 68,0
45 450 76,5
50 500 85,0
A tensão na armadura protendida, σpd, pode ser obtida a partida das expressões empíricas do
ACI, (5.56) e (5.57), no caso de monocordoalhas engraxadas. Para protensão aderente, Pfeil
[28]
, apresenta a seguinte expressão empírica.
σ
γ
ρ−
γ
=σ
cd
s
ptk
p
s
ptk
pd
f
5,01
f
(5.65)
Admitindo:
aço CP-190
γc = 1,4
Efeito Rüsch = 0,85
γs = 1,15
( )p2pd 15,501.16 ρ⋅κ−⋅=σ (kgf/cm2
) (5.66a)
( )p2pd 12,650.1 ρ⋅κ−⋅=σ (MPa) (5.66b)
Tabela 5.3: Valores de κ2 para o cálculo da tensão na armadura protendida aderente
fck fck κκκκ2 κκκκ2
(MPa) (kgf/cm²) (MPa) (kgf/cm²)
20 20 6,79 67,95
25 25 5,44 54,36
30 30 4,53 45,30
35 35 3,88 38,83
40 40 3,40 33,97
45 45 3,02 30,20
50 50 2,72 27,18
A expressão (5.64) é válida para ptkpe f5,0≥σ . No caso do aço CP-190, 2pe
cm
kgf3,488.9≥σ .
Considerando o exemplo anterior, protensão não aderente, tem-se:
1326,0
1,182
846.12
00188,0
cd
pd
pp ==
σ
σ
ρ=ω](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-80-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 79
________________________________________________________________________________
Engº. Alexandre Emerick
cm15,20
434895,10846.1295,3
23434895,1021846.1295,3
fAA
dfAdA
d
ydspdp
sydsppdp
=
⋅+⋅
⋅⋅+⋅⋅
=
+σ
+σ
=
( ) ( ) m/m.kgf241.181326,06,012015,0434895,10846.1295,3MdR =⋅−⋅⋅⋅+⋅=
m/m.kgf707.2015,200,51M 2
LIM,dR =⋅=
B) SEÇÃO T
Além da seção retangular, outra seção bastante usual é a seção T. No caso de lajes
protendidas elas pode ser usada, por exemplo, em vigas ou para a verificação das nervuras, no
caso de lajes nervuradas.
A Figura 5.43 apresenta o esquema de forças em uma seção T no Estádio III considerando o
diagrama retangular equivalente de tensões no concreto.
Figura 5.43: Seção T – E.L.U. Flexão
Nas seções T com mesa de compressão superabundante, é comum obter a posição da linha
neutra dentro da mesa, x ≤ hf. Nesse caso, a seção é dimensionada como uma seção
retangular de largura bf. Essa condição pode ser verificada com a seguinte desigualdade:
cd
pd
pf d4,1h
σ
σ
ρ⋅⋅> (5.67)
Quando x > hf, a seção funciona como T. O momento resistente de projeto de uma seção T
subarmada pode ser calculado com a seguinte expressão:
( )[ ] ( )
−⋅⋅−⋅σ+
σ
σ
⋅
−
−⋅+σ−=
2
h
dhbb
db
AA
6,01dfAAAM f
fwfcd
cd
pd
w
pfp
ydspdpfpdR (5.68)
y=0,8x
bw
bf
0,85 fcd
Rcc
Rpt = Ap σpd
Rst = As σsd
dp
ds
εp
εc
εs
Md
x
Z1
Z2
LN
hf
h
Ap
As](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-81-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 80
________________________________________________________________________________
Engº. Alexandre Emerick
onde, Apf representa a área da armadura protendida necessária para equilibrar as abas da
mesa.
( )
pd
cd
fwfpf hbbA
σ
σ
⋅−= (5.69)
O momento resistente de projeto dado pela expressão (5.68) fica entretanto limitado ao valor
máximo MdR,LIM.
( )
−⋅−σ+σ⋅=≤
2
h
dhbbdb28,0MM f
fwfcdcd
2
wLIM,dRdR (5.70)
5.6.2. ESTADO LIMITE ÚLTIMO NO ATO DA PROTENSÃO
Além da verificação da laje quanto ao Estado Limite Último de ruptura por flexão para a
protensão no tempo infinito e ações externas majoradas com seus coeficientes de cálculo, para
estruturas de concreto protendido em geral deve-se também comprovar a segurança contra
ruptura no ato da aplicação da protensão.
A NBR 7197 [23]
prescreve que a verificação quanto ao E.L.U. no ato da protensão seja feita
considerando o Estado Limite Último de ruptura ou por alongamento excessivo do aço,
considerado como resistência característica do concreto fck,j,correspondente à idade j, em dias,
do material no ato da protensão, sendo que a resistência de fck,j deve ser claramente
especificada no projeto.
Para essa verificação, a NBR 7197 prescreve os seguintes valores para os coeficientes de
ponderação:
γc = 1,2 – concreto;
γs = 1,15 – aço;
γp = 1,1 – cargas oriundas da protensão com pós-tração;
γf = 1,0 – para as ações desfavoráveis e γf = 0,9 para as ações favoráveis
Apenas as cargas que efetivamente atuarem na ocasião da protensão devem ser
consideradas.
5.6.2.1. VERIFICAÇÃO SIMPLIFICADA
A NBR 7197 admite que a segurança em relação ao E.L.U. no ato de protensão esteja
garantida desde que as seguintes condições fiquem satisfeitas:
#"a tensão máxima de compressão na seção de concreto, obtida através das solicitações
ponderadas de γp = 1,1 e γf = 1,0 não ultrapassem 70% da resistência característica
fck,j prevista para a idade de aplicação da protensão;
#"a tensão máxima de tração no concreto não ultrapasse 1,2 vezes a resistência à tração
fctk correspondente ao valor fck,j especificado;
#"quando nas seções transversais existirem tensões de tração, deve haver armadura de
tração calculada no Estádio II, permitindo-se admitir que a força nessa armadura, nessa
fase da construção, seja igual à resultante das tensões de tração no concreto no
Estádio I. Essa força não deve provocar, na armadura correspondente, acréscimos de
tensão superiores a 150 MPa no caso de fios ou barras lisas e a 250 MPa em barras
nervuradas.](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-82-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 81
________________________________________________________________________________
Engº. Alexandre Emerick
5.7. VERIFICAÇÃO À RUPTURA POR CISALHAMENTO
Sobretudo nas lajes apoiadas diretamente sobre pilares ou submetidas a cargas concentradas
importantes é necessário comprovar sua resistência ao esforço cortante ao redor do suporte da
laje ou ao redor da carga concentrada.
De acordo com a NBR 7197 no subitem 9.5.4 a verificação da resistência à punção deve
obedecer ao que prescreve a NBR 6118 (NB-1), permitindo considerar o efeito favorável da
componente da força de protensão perpendicular ao plano médio da laje atuando no contorno
crítico de punção, devendo-se aplicar o coeficiente de minoração 0,8 às forças de protensão no
tempo infinito. Cabe citar que as prescrições da NB-1/78 sobre punção são válidas apenas
para o caso de carga centrada. Quando existirem momentos atuantes deve-se buscar
formulações mais completas como a do MC-90 [18]
ou do ACI 318 [1]
, por exemplo. O PR NB-1
apresenta uma formulação para o cálculo de punção baseada na formulação do CEB.
De acordo com o PR NB-1 na verificação da laje ao puncionamento a tensão tangencial
atuante pode ser reduzida da tensão devida ao efeito dos cabos de protensão inclinados que
atravessam o contorno crítico considerado passando a menos de d/2 da face do pilar. Ou seja:
PdSdefSd,
τ−τ=τ (5.71)
onde:
τSd,ef − tensão tangencial efetiva de cálculo;
τSd − tensão tangencial atuante de cálculo, calculada de acordo com o item 19.4 do
projeto de revisão da NB-1;
τPd − tensão devida ao efeito dos cabos de protensão inclinados que atravessam o
contorno considerado e passam a menos de d/2 da face do pilar conforme indica a
Figura 5.44.
du
senP iiinf,k
Pd
α
=τ
∑ (5.72)
onde:
Pkinf,i − força de protensão no cabo i;
αi − inclinação do cabo i em relação ao plano da laje no contorno considerado
u − perímetro crítico do contorno considerado, em que se calculam τSd,ef e τSd
Figura 5.44: Efeito favorável dos cabos inclinados passando na região dos apoios
Além do efeito dos cabos inclinados passando sobre a região do apoio existe ainda o efeito
favorável da compressão promovida pela protensão na direção perpendicular ao plano da laje.
Entretanto, ao contrário do CEB e do ACI, o PR NB-1 não leva em consideração esse efeito
sendo portanto, mais conservador.
CABO i
b+d
a
b
REGIÃO ONDE PASSAM OS
CABOS QUE ENTRAM NO
CÁLCULO DE τPd
PERÍMETRO CRÍTICO u
αi
2d](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-83-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 82
________________________________________________________________________________
Engº. Alexandre Emerick
5.8. VERIFICAÇÃO AO ESTADO LIMITE DE DEFORMAÇÃO EXCESSIVA −−−− FLECHAS
As flechas em lajes protendidas são calculadas considerando apenas o carregamento não
equilibrado pela protensão. Obtido o valor do deslocamento elástico da laje deve-se levar em
consideração os efeitos da perda de rigidez devido à fissuração, quando essa for importante, e
ainda a deformação lenta.
Para o cálculo do deslocamento elástico, quando não se lança mão de um processo de cálculo
mais rigoroso, como uso de métodos numéricos computacionais (grelhas e elementos finitos,
por exemplo), pode-se usar um processo simplificado a partir do método do pórtico equivalente:
#"ao calcular-se o pórtico na direção x, obtém-se a flecha máxima (wx) no vão
correspondente ao painel que deseja ser estudado;
#"analogamente, obtém-se a flecha wy quando calculado o pórtico na direção y,
correspondente ao mesmo painel de laje cogumelo para o qual foi obtida a flecha wx;
#"a flecha total no centro do painel será igual à soma das flechas nas direções x e y
(Figura 5.45).
wTotal = wx + wy (5.73)
Figura 5.45: Cálculo aproximado da flecha pelo processo de pórticos equivalentes
Outra indicação interessante pode ser obtida no Boletim 158 do CEB [9]
que apresenta um
conjunto de tabelas práticas para o cálculo da flecha em lajes cogumelo.
5.9. COMBINAÇÕES DE AÇÕES
A norma brasileira NBR 8681 [26]
estabelece os critérios com relação às ações e combinações
para o projeto de estruturas usuais da construção civil. A seguir é apresentado um breve
resumo das combinações de ações previstas pela norma brasileira de interesse no projeto de
lajes protendidas.
5.9.1. COMBINAÇÕES EM SERVIÇO
De acordo com a NBR 8681 item 5.5.1:
#"Combinações quase permanentes
∑∑ ==
Ψ+=
n
1j
k,Qjj2
m
1i
k,Giuti,d FFF (5.74)
#"Combinações freqüentes
∑∑ ==
Ψ+Ψ+=
n
2j
k,Qjj2k,1Q1
m
1i
k,Giuti,d FFFF (5.75)
wy
wx
wTotal
X
Y](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-84-320.jpg)

![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 84
________________________________________________________________________________
Engº. Alexandre Emerick
6. CÁLCULO DAS PERDAS DE PROTENSÃO
De acordo com Pfeil [28]
, perdas de protensão são todas as perdas verificadas nos esforços
aplicados aos cabos de protensão. As perdas de protensão podem ser classificadas em dois
grupos:
a) Perdas imediatas: são as que se verificam durante a operação de protensão e
ancoragem dos cabos, a saber:
#"Perdas por atrito, produzidas por atrito do cabo com peças adjacentes durante a
protensão.
#"Perdas nas ancoragens, provocadas por movimentos nas cunhas de ancoragem,
quando o esforço é transferido do macaco para as placas de apoio.
#"Perdas por encurtamento elástico do concreto.
b) Perdas retardadas: são as que se processam ao longo de vários anos, a saber:
#"Perdas por retração e fluência do concreto, produzidas por encurtamentos retardados
do concreto, decorrentes do comportamento viscoso deste complexo material.
#"Perdas por relaxação do aço, produzidas por quedas de tensão nos aços de alta
resistência quando ancorados nas extremidades sob tensão elevada.
6.1. PERDAS IMEDIATAS
6.1.1. PERDAS POR ATRITO
As perdas por atrito são calculadas pela expressão 6.1.
)kx(
oe)x(
+αµ− ∑σ=σ (6.1)
sendo:
σ(x) – tensão atuante no cabo a uma distância x;
σo – tensão inicial aplicada na extremidade do cabo;
Σα – soma dos ângulos de desvio previstos em radianos;
µ – coeficiente de atrito aparente entre o cabo e a bainha:
Em geral adota-se:
µ = 0,20 para cordoalhas em bainhas metálicas;
µ = 0,05 para cordoalhas em bainhas de polipropileno lubrificadas.
k – coeficiente de perdas por metro provocadas por curvas não intencionais do cabo.
Em geral adota-se:
k = entre 0,001 a 0,003 m-1
6.1.2. PERDAS POR CRAVAÇÃO DA ANCORAGEM
A região de influência devido à perda por cravação da ancoragem (acomodação das cunhas)
pode ser avaliada através de um cálculo iterativo simples:
1º PASSO: arbitra-se um valor para x (onde x é a região de influência da cravação)](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-86-320.jpg)

![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 86
________________________________________________________________________________
Engº. Alexandre Emerick
6.2. PERDAS DIFERIDAS NO TEMPO
As perdas no tempo levam em consideração as perdas devido aos fenômenos de fluência e
retração do concreto e relaxação do aço.
A formulação de cálculo das perdas diferidas no tempo apresentado a seguir é baseada nas
prescrições do Código Modelo Europeu – MC-90 [18]
.
De acordo com o MC-90 as perdas finais podem ser estimadas pela expressão 6.5:
[ ]
ϕ⋅χ+⋅
σ
σ
α−
ϕ⋅σ+σ⋅α+σ∆+ε
=σ∆ ++
)t,t()t,t(
)t(E
E
)t(
)t(
1
)t,t()t()t(E)t,t(
oo
oc
28c
oP
oCP
ooCPoCgPrpscs
rsc,P (6.5)
onde:
εcs (t,ts) = retração do concreto;
Ep = módulo de elasticidade do aço de protensão;
∆σPr = perda por relaxação pura do aço adotando como tensão de referência:
σP = σPo – 0,3 ∆σP,c+s+r
σPo = tensão inicial nos cabos (já descontadas as perdas iniciais) com ∆σP,c+s+r valor
estimado em torno de 10 a 15% dependendo se o aço é de relaxação normal ou baixa;
σCg (to) = tensão no concreto na altura dos cabos de protensão devido às cargas
mobilizadas na protensão (em geral cargas permanentes);
σCP (to) = tensão no concreto na altura dos cabos devido à força de protensão;
ϕ (t,to) = coeficiente de fluência do concreto;
α = Es / Ec28;
σP(to) = tensão no aço no instante to (já descontadas as perdas iniciais);
χ (t,to) = coeficiente de envelhecimento:
0,8 se 10 dias < to < 30 dias
χ (t,to) = (6.6)
to
0,5
/ (1+ to
0,5
)
Com relação ao módulo de elasticidade do concreto, o PR NB-1 prescreve que na falta de
dados experimentais mais precisos pode ser adotado:
2
1
ck28c f5600E ⋅= em (MPa) (6.7)
De acordo com o projeto de revisão da NB-1 a expressão 6.7 é válida para o cálculo do modulo
de elasticidade inicial em uma idade t > 7 dias, substituindo o valor de fck por fck,j. Para idades
inferiores a 7 dias o PR NB-1 não apresenta indicação.
Como atualmente tem sido aplicado protensão em lajes com idades de 4 e até mesmo 3 dias,
pode-se simplificadamente calcular Ec(to) com a expressão 6.7, porém deve-se exigir no projeto
a comprovação da resistência mínima fck,j, antes de protender os cabos, com a ruptura de
corpos-de-prova, sendo recomendável também a comprovação do módulo de elasticidade
mínimo na idade de protensão.](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-88-320.jpg)

![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 88
________________________________________________________________________________
Engº. Alexandre Emerick
T(∆ti) = temperatura em ºC no intervalo ∆ti
To = 1 ºC
A outra parcela da equação (6.8) é calculada a partir de (6.15):
3,0
1
o
H
1
o
oc
t
)tt(
t
)tt(
)tt(
−
+β
−
=−β (6.15)
dias1500250
h
h
RH
RH
2,11150
o
fic
18
o
H ≤+
+⋅=β (6.16)
Quando o valor de t - to tende ao infinito o termo βc(t - to) tende a 1.
6.2.2. CÁLCULO DA RETRAÇÃO DO CONCRETO
Para concreto com temperatura ambiente em torno de 20 ºC, segundo o MC-90 a retração do
concreto pode ser estimada pela expressão 6.13:
( ) )tt(tt sscsoscs −βε=−ε (6.17)
sendo,
ts – tempo para a cura do concreto, em geral, 3 dias
RH28cmscso )f( β⋅ε=ε (6.18)
6
cmo
cm
sc28cms 10
f
f
910160)f( −
⋅
−⋅β+=ε (6.19)
ββββsc TIPO DE CIMENTO
4 RS – cimento de endurecimento rápido (ARI)
5 N, R – cimento de endurecimento normal a rápido
8 SL – cimento e endurecimento lento
%99RH%40/p
RH
RH
155,1
3
O
≤≤→
−⋅−
=βRH (6.20)
%99RH/p25,0 ≥→+
2
1
1
s
o
fic
1
s
sS
t
tt
h
h
350
t
tt
)tt(
−
+
⋅
−
=−β (6.21)
A Tabela 6.1, extraída da NBR 7197 [23]
, fornece o valor para o coeficiente de fluência e de
retração do concreto em função da umidade ambiente e da espessura equivalente (hfic = 2Ac/u).
Em casos onde não há grande necessidade de precisão, pode-se obter os valores de ϕ (t∞,to) e
εcs (t∞,to) por interpolação. Os valores da Tabela 6.1 são admitidos válidos para temperaturas do
concreto variando entre 0º e 40ºC e concretos plásticos com cimento Portland comum.](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-90-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 89
________________________________________________________________________________
Engº. Alexandre Emerick
Tabela 6.1: Valores característicos superiores da deformação específica de retração εcs(t∞,to) e
do coeficiente de fluência ϕ(t∞,to)
Umidade ambiente
(%)
40% 55% 75% 90%
Espessura Equivalente
2Ac/u
(cm)
20
60
20
60
20
60
20
60
5 4,4
3,9
3,8 3,3 3,0 2,6 2,3 2,1
ϕϕϕϕ(t∞∞∞∞,to)
30 3,0
2,9
2,6 2,5 2,0 2,0 1,6 1,6to(dias)
60 3,0
2,6
2,2 2,2 1,7 1,8 1,4 1,4
5 -0,44
-0,39
-0,37
-0,33
-0,23
-0,21
-0,10
-0,09
εεεεcs(t∞∞∞∞,to)
(‰)
30 -0,37
-0,38
-0,31
-0,31
-0,20
-0,20
-0,09
-0,09
to(dias)
60 -0,32
-0,36
-0,27
-0,30
-0,17
-0,19
-0,08
-0,09
Fonte: NBR 7197 [23]
6.2.3. CÁLCULO DA RELAXAÇÃO DO AÇO
A relaxação de cordoalhas, após 1000 horas a 20ºC, obtida em ensaios descritos na NBR 7484
[25]
não deve superar os valores limites descritos na NBR 7483 [24]
. Para efeito de projeto podem
ser adotados os valores apresentados na Tabela 6.2:
Tabela 6.2: Valores de relaxação em 1000 horas (ρ1000(%)) para cordoalhas brasileiras
Aço de relaxaçãoσσσσPo
Normal Baixa
0,5 fptk 0,0 0,0
0,6 fptk 3,5 1,3
0,7 fptk 7,0 2,5
0,8 fptk 12,0 3,5
Fonte: Projeto de revisão da NB-1
Sendo:
PoPr (%) σ⋅ρ=σ∆ (6.22)
Segundo o MC-90 a porcentagem de relaxação em uma idade t horas pode ser avaliada por:
k
1000t
1000
t
(%)(%)
⋅ρ=ρ (6.23)
onde,
ρ
ρ
=
100
1000
logk (6.24)
onde, k pode ser adotado como:
k = 0,12 – aços de relaxação normal
k = 0,19 – aços de relaxação baixa
De acordo como o catálogo técnico da Belgo Mineira [5]
a diferença entre os aços de relaxação
normal e baixa ocorre devido tipo de tratamento recebido no final do processo de fabricação:](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-91-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 91
________________________________________________________________________________
Engº. Alexandre Emerick
7. EXEMPLO DE CÁLCULO DE UMA LAJE LISA
PROTENDIDA
O exemplo apresentado diz respeito ao cálculo de uma faixa de uma laje protendida hipotética.
A faixa será calculada considerando o processo de pórtico equivalente do ACI 318 [1]
.
A Figura 7.1. mostra a laje em planta, observe que a geometria da laje é bastante simples com
vãos dentro das recomendações apresentadas no item 4.2 desse trabalho, valendo ressaltar
que na prática os projetos são bem mais complexos e que o objetivo desse exemplo é apenas
ilustrar o processo de cálculo.
200
300
300
20
200
200 800 800 800 200
800
800
800
800
A A
CORTE A-A
PLANTA BAIXA
Figura 7.1: Laje lisa que será
estuda no exemplo
FAIXA CALCULADA NO EXEMPLO
PILARES COM 40 x 40
Dimensões em cm](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-93-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 92
________________________________________________________________________________
Engº. Alexandre Emerick
Figura 7.2: Pórtico equivalente – vista em 3D
Considere ainda para o cálculo:
• Armadura ativa: Monocordoalhas engraxadas – CP 190 RB – ∅ 12,7mm
• Armadura passiva: CA-50 e CA-60
• Concreto: fck = 30 MPa
• Idade da protensão: 5 dias
• Resistência do concreto na idade de protensão:
• fck,5 = 30 exp{0,25[1−(28/5)1/2
]} ≅ 21 MPa
• Módulo de elasticidade:
• Inicial – Ec28 = 5600 (30)1/2
= 30.672 MPa
• Secante – Ecs = 0,85Ec28 = 26.071 MPa
• Na idade de protensão – Ec5 = 5600 (21)1/2
= 25.662 MPa
• Resistência característica à tração:
• fctk = 0,21(30)2/3
= 2,03 MPa
• fctk,5 = 0,21(21)2/3
= 1,60 MPa
• Resistência média à tração:
• fct,m = 0,30(30)2/3
= 2,90 MPa
7.1. ESPESSURA DA LAJE
Para lajes lisas pode-se adotar com espessura 1/40 do vão, o que fornece uma espessura de
20 cm.
7.2. CARREGAMENTOS ATUANTES NA LAJE
Considere que a utilização do pavimento seja para escritórios e ainda que as divisões internas
dos ambientes sejam feitas com divisórias, existindo alvenaria somente ao longo do contorno
da laje. Dessa forma, podemos considerar os seguintes carregamentos atuantes:
Peso próprio ................... : 500 kgf/m2
(5 kN/m2
)
Sobrecarga ...................... : 200 kgf/m2
(2 kN/m2
)
Revestimento ................... : 100 kgf/m2
(1 kN/m2
)
Divisórias .......................... : 100 kgf/m2
(1 kN/m2
)
Alvenaria no contorno da laje (espessura 15 cm): 540 kgf/m.
7.3. DEFINIÇÃO DO CARREGAMENTO A SER EQUILIBRADO COM A PROTENSÃO
Em geral, adota-se para o carregamento a ser equilibrado o peso próprio acrescido de uma
parcela do carregamento total. O ACI 423 [2]
recomenda que quando sejam previstas paredes](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-94-320.jpg)
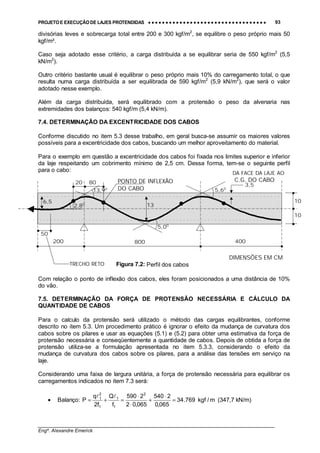

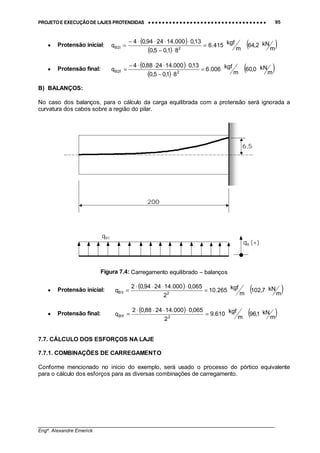
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 96
________________________________________________________________________________
Engº. Alexandre Emerick
• COMB. 1: G1 + 1,1qBi – verificação da ruptura no ato da protensão.
• COMB. 2: G1 + G2 + PAR + Q1 + Q2 + qBf – verificação das tensões do ACI 423 [2]
.
• COMB. 3: G1 + G2 + PAR + 0,2(Q1 + Q2) + qBf − combinação quase permanente.
• COMB. 4: G1 + G2 + PAR + 0,3Q2 + 0,2Q1 + qBf − combinação freqüente.
• COMB. 5: verificação quanto ao estado limite último (flexão e cisalhamento)
5.1: 1,4 (G1 + G2 + PAR + Q1 + Q2) + 1,2 FHIP
5.2: 1,4 (G1 + G2 + PAR + Q1 + Q2) + 0,9 FHIP
onde:
G1 – peso próprio = 500 kgf/m² × 8m = 4.000 kgf/m (40 kN/m)
G2 – revestimento = 100 kgf/m² × 8m = 800 kgf/m (8 kN/m)
PAR – peso da alvenaria na extremidade do balanço = 540 kgf/m × 8m = 4.320 kgf (43,2 kN)
Q1 – divisórias = 100 kgf/m² × 8m = 800 kgf/m (8 kN/m)
Q2 – sobrecarga = 200 kgf/m² × 8m = 1.600 kgf/m (16 kN/m)
qBi – carga uniforme distribuída balanceada com a protensão inicial
qBf – carga uniforme distribuída balanceada com a protensão final
FHIP – efeito hiperestático de protensão (γp = 1,2 se desfavorável e γp = 0,9 se favorável)
7.7.2. PÓRTICO EQUIVALENTE SEGUNDO O ACI 318 [1]
Para a análise dos esforços na laje foi utilizado o método do pórtico equivalente segundo o ACI
318. A Tabela 7.1 apresenta o calculo do comprimento equivalente dos pilares.
Tabela 7.1: Cálculo do comprimento equivalente dos pilares
c1
(cm)
c2
(cm)
L
(cm)
ΣΣΣΣkc
(cm³×Ec)
L2
(cm)
x
(cm)
y
(cm)
C
(cm4
)
kT
(cm³×Ec)
kec
(cm³×EC)
Leq
(cm)
40 40 300 6.770 800 20 40 73.067 1.917 1.494 571
O momento de inércia da laje na região do pilar é dado por:
As Figuras 7.5 a 7.8 apresentam os diagramas de momentos obtidos para as diversas
combinações de carregamento.
20
LAJE
BARRA COM MOM. DE
INÉRCIA EQUIVALENTE (Ieq)
BARRA COM MOM. DE
INÉRCIA DA LAJE (Ilaje)
40
PILAR
4
2
3
2
2
2
laje
eq cm951.590
800
40
1
12
80020
c
1
I
I =
−
⋅
=
−
=
!
A altura equivalente da laje fica:
43
eq cm7,20
800
951.59012
h =
⋅
=
Figura 7.4: Cálculo da inércia equivalente na
ligação laje-pilar](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-98-320.jpg)
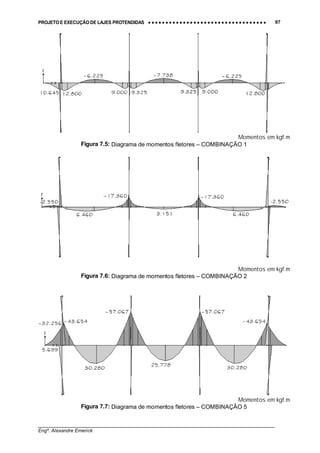
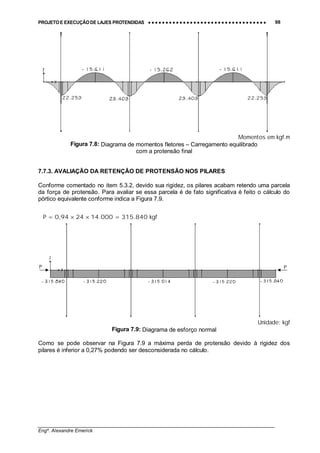
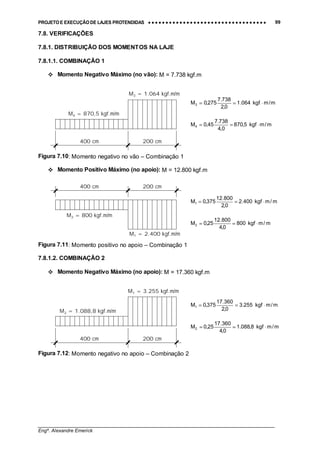

![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 101
________________________________________________________________________________
Engº. Alexandre Emerick
Tabela 7.3: Momentos negativos distribuídos
VÃO MTOTAL (kgf.m) M3 (kgf.m/m) M4 (kgf.m/m)
1 30.280 4.164 3.407
2 25.778 3.545 2.900
3 30.280 4.164 3.407
7.8.2. TENSÕES EM SERVIÇO – RECOMENDAÇÕES DO ACI 423 [2]
Considerando as recomendações do ACI 423 para laje com protensão não aderente tem-se:
• Tensão média de compressão na laje:
%" Limites: 0,86 MPa < σc < 3,5 MPa
%" Protensão inicial: MPa97,1
cm
kgf7,19
80020
94,01400024
2cMÁX ==
⋅
⋅⋅
=σ
%" Protensão final: MPa85,1
cm
kgf5,18
80020
88,01400024
2cMÍN ==
⋅
⋅⋅
=σ
• Tensões no concreto imediatamente após a aplicação da protensão, em MPa:
Limites:
(a) compressão na zona de momento negativo = MPa4,8214,0'f40,0 ci =⋅=⋅
(b) compressão na zona de momento positivo = MPa6,12216,0'f60,0 ci =⋅=⋅
(c) tração (com armadura passiva) = MPa3,2215,0'f50,0 ci =⋅=
Tensões atuantes – considerando a combinação 1 de carregamentos:
Equação geral para o cálculo das tensões:
W
M
A
P
±=σ (Estádio I)
onde:
b = 1 metro
m/kgf480.3994,0000.14
8
24
P =⋅⋅= (394,8 kN/m)
2
cm000.210020A =⋅=
3
2
cm67,666.6
6
20100
W =
⋅
=
(a) compressão na zona de momento negativo:
( )MPa57,3
cm
kgf7,35
67,666.6
400.106
000.2
480.39
2=+ → OK
(b) compressão na zona de momento positivo:
( )MPa57,5
cm
kgf7,55
67,666.6
000.240
000.2
480.39
2=+ → OK
(c) tração (com armadura passiva)
( )MPa63,1
cm
kgf26,16
67,666.6
000.240
000.2
480.39
2 −−=− → OK
(o sinal negativo indica que existe tração na seção)](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-103-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 102
________________________________________________________________________________
Engº. Alexandre Emerick
• Tensões no concreto em serviço (após as perdas no tempo), em MPa:
Limites:
(a) compressão na zona de momento negativo = MPa0,93030,0 =⋅
(b) compressão na zona de momento positivo = MPa5,133045,0 =⋅
(c) tração (com armadura passiva) = MPa74,23050,0 =
Tensões atuantes – considerando a combinação 2 de carregamentos:
m/kgf960.3688,0000.14
8
24
P =⋅⋅=∞ (369,6 kN/m)
(a) compressão na zona de momento negativo:
( )MPa7,6
cm
kgf3,67
67,666.6
500.325
000.2
960.36
2=+ → OK
(b) compressão na zona de momento positivo:
( )MPa2,3
cm
kgf8,31
67,666.6
25,888
000.2
960.36
2=+ → OK
(c) tração (com armadura passiva):
( )MPa52,0
cm
kgf15,5
67,666.6
25,888
000.2
960.36
2=− → OK
(o sinal positivo indica compressão na seção)
Portanto, as tensões atuantes na laje atendem as recomendações do ACI 423 [2]
para lajes com
protensão não aderente.
7.8.3. ESTADO LIMITE ÚLTIMO NO ATO DA PROTENSÃO
Para a combinação 1 de carregamentos deve-se atender:
(a) Tensão máxima de compressão = MPa7,142170,0f70,0 j,ck =⋅=⋅
σcMÁX = 5,57 MPa
(b) Tensão máxima de tração = MPa92,160,120,1f20,1 j,ctk =⋅=⋅
σtMÁX = 1,63 MPa
Portanto, atende ao E.L.U. no ato da protensão, segundo o critério simplificado da NBR 7197.
7.8.4. TENSÃO DE TRAÇÃO PARA A COMBINAÇÃO QUASE PERMANENTE DAS AÇÕES
Para a combinação quase permanente das ações (combinação 3) o máximo momento fletor
obtido, em módulo, foi:
MMÁX,COM.3 = 6.134 kgf.m (61,34 kN.m)](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-104-320.jpg)






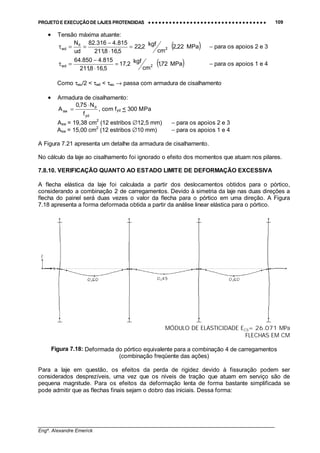



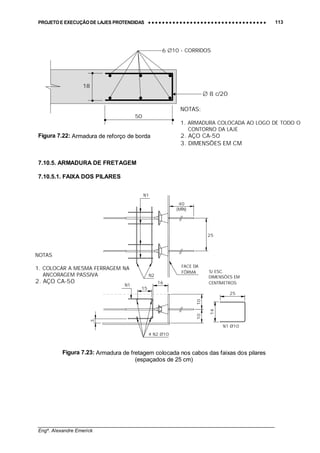
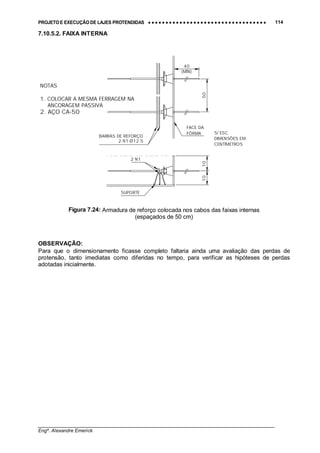
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 115
________________________________________________________________________________
Engº. Alexandre Emerick
8. REFERÊNCIAS BIBLIOGRÁFICAS
[1] ACI 318 – Building Code Requirements for Structural Concrete. Commitee 318. Detroit,
1995.
[2] ACI 423 – Recommendations for Concrete Members Prestressed with Unbounded Tendons.
Commitee 423. Detroit, 1983.
[3] AALAMI, Bijan O. – ADAPT – Post-tentionig Manual, California, USA, 1996.
[4] AALAMI, Bijan O. – Load Balancing: A Comprehensive Solution to Post-Tensioning – ACI
Structural Journal, Title no
. 87-S68, USA 1990.
[5] BELGO MINEIRA – Catálogo Técnico.
[6] CAMPUS, A.D. – Influência da Protensão na Carga dos Pilares, TQS News Nº.16, 2002.
[7] CAUDURO, E.L. – Recomendações para a Boa Execução de Construções em Concreto
Protendido com Cordoalhas Engraxadas e Plastificadas (Protensão Não Aderente) – Revista
IBRACON Nº. 28, 2002.
[8] CAUDURO, E.L. & LEME, A.J.H – A Protensão em Edifícios sem Vigas – Novas Técnicas
Aumentam a Qualidade e Reduzem o Custo Total do Edifício – 41º Congresso Brasileiro do
Concreto – IBRACON, Salvador, 1999.
[9] CEB – Design Manual on Cracking and Deformations, (Boletin Nº 158) – 1985.
[10] CLÍMACO, J.C.T.S. - Estruturas de Concreto Armado 1 - Notas de Aula, Departamento de
Engenharia Civil, Universidade de Brasília – 1999.
[11] FRANCO, M. – Concreto Protendido em Edifícios: Problemas Particulares.
[12] FREYSSINET – Catálogo Técnico.
[13] FUSCO, P.B – Técnicas de Armar as Estruturas de Concreto, Ed. PINI, São Paulo, 1995.
[14] IMPACTO PROTENSÃO – Manual de Procedimentos de Campo para Execução de
Estruturas com Protensão em Monocordoalhas Não Aderentes, Fortaleza 1998.
[15] LIN, T.Y. – Design on Prestressed Concrete Structures, 2º Ed. New York, USA – 1963.
[16] MAC Protensão – Catálogo Técnico.
[17] MARTINS, P.C.R. – Concreto Protendido – Notas de Aula, Universidade de Brasília 2000.
[18] MC-90 – Código Modelo CEB/FIP, 1990.
[19] MORAES, M.C. – Concreto Protendido: Introdução ao Uso da Cordoalha Engraxada
Plastificada – Caderno de Estrutura Nº 14, Brasília – 1999.
[20] NAAMAN, A.E. – Prestressed Concrete Analysis and Design, New York, USA – 1982.
[21] NBR 6118 (NB-1) – Projetos e Execução de Estruturas de Concreto Armado, ABNT –
1982.
[22] NBR 6118 (NB-1) Projeto de Revisão – Projetos de Estruturas de Concreto, ABNT – 2000.](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-117-320.jpg)
![PROJETO E EXECUÇÃO DE LAJES PROTENDIDAS •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• •••• 116
________________________________________________________________________________
Engº. Alexandre Emerick
[23] NBR 7197 – Projetos de Estruturas de Concreto Protendido, ABNT – 1989.
[24] NBR 7483 – Cordoalhas de Aço para Concreto Protendido, ABNT – 1990.
[25] NBR 7484 – Fios, Barras e Cordoalhas de Aço Destinados a Armadura de Protensão –
Ensaio de Relaxação Isotérmica, ABNT – 1990.
[26] NBR 8981 – Ações e Segurança nas Estruturas, ABNT – 1984.
[27] PARK, R e GAMBLE, W.L. – Reinforced Concrete Slabs. New York, USA – 1980.
[28] PFEIL, W. – Concreto Protendido, Vol. 1, Ed. LTC, 2o
Ed., Rio de Janeiro, 1988
[29] PROTENDE – Catálogo Técnico.
[30] PTI – Field Procedures Manual for Unbonded Single Strand Tendons, 1994.
[31] Revistas Téchne, Edições: Janeiro – 1997 e Junho – 1999.
[32] RUDLOFF – VSL – Catálogo Técnico, 1993.
[33] SCHMID, M.T. – Lajes Cogumelo Protendidas. In: Reunião Anual do IBRACON – Colóquio
Sobre Concreto Protendido. São Paulo – 1984.
[34] SCHMID, M.T. – SPANN-LAJES – Manual do Usuário Versão 4.0, Curitiba, PR – 1999.
[35] Sistema Freyssinet de Lajes Protendidas – Catálogo Técnico.
[36] SOUZA, V.C.M. & CUNHA, A.J.P. – Lajes em Concreto Armado e Protendido, 2º Ed., Rio
de Janeiro, 1998.
[37] VERÍSSIMO, G.S. & CÉSAR Jr, K.L.M. – Concreto Protendido – Fundamentos Básicos, 4º
Ed., Universidade Federal de Viçosa, 1998.](https://image.slidesharecdn.com/lp-130929115617-phpapp01/85/Lajes-Protendidas-118-320.jpg)