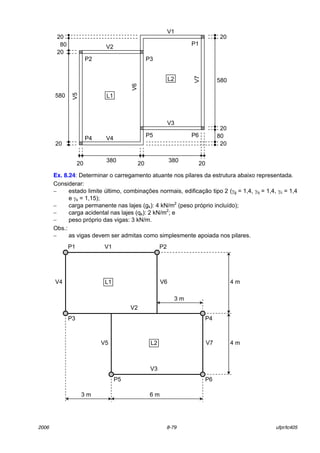
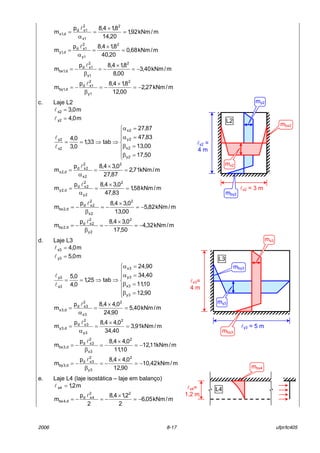
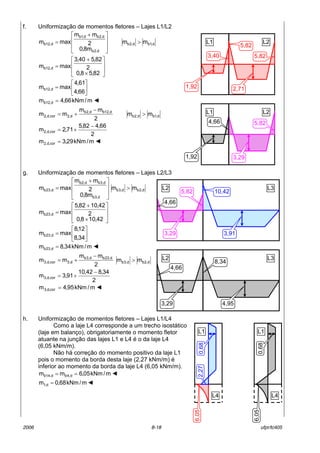
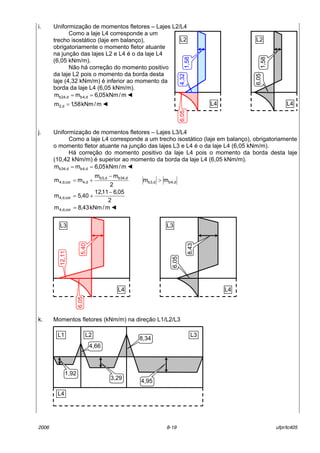
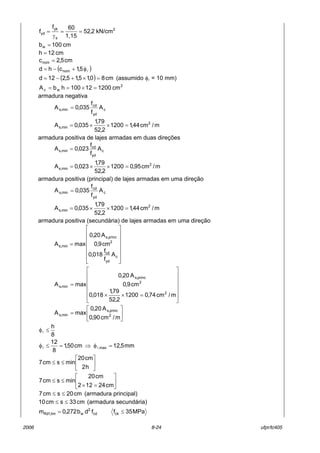
O documento descreve as características de lajes maciças de concreto armado. Apresenta definições de elementos estruturais laminares como placas, cascas e chapas. Descreve tipos de lajes como lisas, nervuradas e mistas. Aborda conceitos como vãos efetivos, curvaturas em uma ou duas direções, continuidade e espessura de lajes. Detalha cargas atuantes como permanentes, decorrentes do peso próprio dos materiais, e acidentais, dependendo do uso do espaço.

1. 2006 8-1 ufpr/tc405
88LAJES MACIÇAS DE CONCRETO ARMADO1
8.1 Introdução
Na teoria das estruturas, consideram-se elementos de superfÌcie aqueles em que uma
dimens„o, usualmente chamada espessura, È relativamente pequena em face das demais,
podendo receber as seguintes denominaÁıes (Figura 8.1):
− placas: elementos de superfÌcie plana sujeitos principalmente a aÁıes normais ao seu
plano;
− cascas: elementos de superfÌcie n„o plana; e
− chapas: elementos de superfÌcie plana sujeitos principalmente a aÁıes contidas em
seu plano.
Figura 8.1 ñ Estruturas laminares
As lajes maciÁas de concreto armado constituem estruturas laminares, tipo placa. Em casos
especiais, onde se requer
lajes com maior rigidez
(maior altura), pode-se
fazer uso de lajes
nervuradas (Figura 8.2).
Figura 8.2 ñ Lajes maciÁas e nervuradas
Quando for desejado que a superfÌcie inferior das lajes nervuradas se torne contÌnua e
plana, fecham-se os vazios com elementos inertes (tijolos,
blocos vazados de concreto, isopor, etc.), como mostrado
na Figura 8.3. Esta laje È denominada mista.
Figura 8.3 ñ Lajes mistas
As lajes que se apÛiam diretamente sobre pilares s„o denominadas lajes lisas e as lajes que
se apÛiam sobre pilares com capitÈis denominam-se lajes cogumelo.
Neste CapÌtulo somente ser„o abordadas as lajes maciÁas apoiadas em vigas.
1
Este capÌtulo È uma cÛpia adaptada da publicaÁ„o LAJES USUAIS DE CONCRETO ARMADO de Roberto
Dalledone Machado.
placa casca chapa
laje maciÁa laje nervurada

2. 2006 8-2 ufpr/tc405
8.2 Vãos efetivos de lajes
Segundo a ABNT NBR 6118, item 14.7.2.2, quando os apoios puderem ser considerados
suficientemente rÌgidos quanto ‡ translaÁ„o vertical, o v„o efetivo (Figura 8.4) deve ser calculado
pela seguinte express„o:
210ef aa ++= ll EquaÁ„o 8.1
com






=






=
h3,0
t5,0
mina
h3,0
t5,0
mina
2
2
1
1
onde:
lef v„o efetivo da laje;
l0 dist‚ncia entre faces de dois apoios (vigas) consecutivos;
t comprimento do apoio paralelo ao v„o da laje analisada;
h espessura da laje.
Figura 8.4 ñ V„o efetivo de laje
8.3 Curvaturas de lajes
As lajes maciÁas de concreto armado (Figura 8.5) podem apresentar:
− curvatura em uma
sÛ direÁ„o; ou
− curvaturas em duas
direÁıes ortogonais.
Figura 8.5 ñ Curvaturas de lajes
Quando a laje apresenta curvatura em uma sÛ direÁ„o, seu comportamento È idÍntico ao de
uma viga de larga base e pouca altura. As lajes com curvaturas em duas direÁıes ortogonais tÍm
comportamento de placa.
h
t2t1
l0
lef
laje
viga
ly
lx
ly
lx

3. 2006 8-3 ufpr/tc405
As lajes com curvatura em uma sÛ direÁ„o s„o apoiadas nas bordas perpendiculares ao
eixo da curvatura, ao passo que as lajes com curvaturas em duas direÁıes ortogonais s„o
apoiadas em todo seu contorno (Figura 8.5).
Quando a relaÁ„o entre o v„o maior (ly) e v„o menor (lx) superar dois, a critÈrio do
projetista, a curvatura na direÁ„o do v„o maior pode ser desprezada. Nesta condiÁ„o somente a
curvatura (esforÁos) na direÁ„o do v„o menor ser· considerada.
As lajes consideradas como de curvatura em uma sÛ direÁ„o s„o tambÈm chamadas lajes
armadas em uma sÛ direÁ„o. As
de curvaturas em duas direÁıes
ortogonais s„o denominadas
armadas em duas direÁıes
(Figura 8.6).
Figura 8.6 ñ Lajes armadas em uma ou duas direÁıes
8.4 Lajes contínuas
Assim como as vigas, as lajes apresentam, tambÈm, condiÁıes de continuidade. Desta
forma os apoios podem ser:
− apoio simples, onde a extremidade da laje È considerada rotulada, transmitindo ‡ viga
suporte somente cargas verticais (reaÁ„o de apoio);
− apoio contÌnuo, onde duas lajes contÌguas transmitem somente cargas verticais
(reaÁ„o de apoio) para a viga suporte; e
− borda livre, onde a extremidade da laje È considerada em balanÁo.
A consideraÁ„o de apoios simples em lajes de extremidade evita que sejam transmitidos
momentos torÁores para as vigas suportes.
Na determinaÁ„o dos esforÁos de um painel de laje, È pr·tica comum considerar as lajes
isoladamente. Como em regiıes de continuidade de lajes existe momento negativo, este pode ser
representado, nas lajes isoladas, por um engaste (Figura 8.7).
Nesta Figura 8.7,
− o apoio simples È representado por uma linha contÌnua;
− o engaste È representado pela hachura; e
− a borda livre È representada por uma linha tracejada.
Ainda na Figura 8.7,
− a laje L1 È considerada simplesmente apoiada nas vigas V1 e V4, contÌnua na direÁ„o
da laje L2 (apoiada sobre a V5) e contÌnua na direÁ„o da laje L3 (apoiada sobre a V2);
− a laje L2 È considerada simplesmente apoiada nas vigas V1 e V3, contÌnua na direÁ„o
das lajes L1 e L3 (apoiada sobre a V5) e com uma borda livre; e
− a laje L3 È considerada simplesmente apoiada nas vigas V3 e V4, contÌnua na direÁ„o
da laje L1 (apoiada sobre a V2) e contÌnua na direÁ„o da laje L2 (apoiada sobre a V5).
ly
lx
ly
lx

4. 2006 8-4 ufpr/tc405
Figura 8.7 ñ Lajes contÌnuas
Quando sobre um apoio comum, duas lajes contÌguas apresentarem diferentes dimensıes,
considera-se o engaste no v„o maior se este for igual ou superior a 2/3 do v„o menor (Figura 8.8).
Deve ser observado na Figura 8.8 que a laje L1 dever· sempre ser considerada como
engastada na direÁ„o da laje L2.
V1
V3
V4
V2
V5
P1 P2
P3 P4
L1
L2
L3
L1
L3
L2
V1
V2
V4 V5
V2
V5V4
V3
V1
V5
V3

5. 2006 8-5 ufpr/tc405
Figura 8.8 ñ Lajes contÌnuas de diferentes dimensıes
8.5 Espessura de lajes
A fixaÁ„o da espessura das lajes deve atender ‡s exigÍncias dos esforÁos solicitantes
(momento fletor e forÁa cortante) para o estado limite ˙ltimo, bem como ‡s verificaÁıes do estado
limite de serviÁo (flechas, vibraÁıes, fissuraÁ„o, etc).
Segundo a ABNT NBR 6118, item 13.2.4.1, nas lajes maciÁas devem ser respeitados os
seguintes limites mÌnimos para as espessuras:
− 5 cm para lajes de cobertura n„o em balanÁo;
− 7 cm para lajes de piso ou de cobertura em balanÁo;
− 10 cm para lajes que suportem veÌculos de peso total menor ou igual a 30 kN; e
− 12 cm para lajes que suportem veÌculos de peso total maior que 30 kN.
8.6 Cargas atuantes nas lajes
As cargas atuantes nas lajes podem ser:
− permanentes, devidas ao peso prÛprio, contra-piso, revestimento, paredes, etc.; e
− acidentais, decorrentes das condiÁıes de uso da laje (residÍncia, escritÛrio, escola,
biblioteca, etc.).
8.6.1 Cargas permanentes
Segundo a ABNT NBR 6120, os pesos especÌficos dos materiais de construÁ„o que
eventualmente possam constituir carregamento em lajes podem ser tomados como sendo:
argamassa de cal, cimento e areia ......................................................................... 19,0 kN/m3
argamassa de cimento e areia ................................................................................ 21,0 kN/m3
argamassa de gesso ............................................................................................... 12,5 kN/m3
reboco ..................................................................................................................... 20,0 kN/m3
concreto simples ..................................................................................................... 24,0 kN/m3
concreto armado ..................................................................................................... 25,0 kN/m3
21
3
2
ll ≥L1
L2
l1
l2
L1
L2
21
3
2
ll <L1
L2
l1
l2
L1
L2

6. 2006 8-6 ufpr/tc405
O carregamento atuante na laje (peso por unidade de ·rea) È dado pela express„o:
hg matγ= EquaÁ„o 8.2
onde:
g carga permanente uniformemente distribuÌda, geralmente em kN/m2
;
γmat peso especÌfico do material, geralmente em kN/m3
; e
h espessura do material, geralmente em m.
Para materiais de acabamento ou coberturas, podem ser adotados os seguintes valores,
considerando pesos por unidade de ·rea:
cer‚mica ................................................................................................................. 0,70 kN/m2
tacos ....................................................................................................................... 0,65 kN/m2
cobertura de telhas francesas (com vigamento) .................................................... 0,90 kN/m2
cobertura de telhas coloniais (com vigamento) ...................................................... 1,20 kN/m2
cobertura de fibro-cimento (com vigamento) .......................................................... 0,30 kN/m2
cobertura de alumÌnio (com vigamento) ................................................................. 0,16 kN/m2
8.6.2 Cargas acidentais
A ABNT NBR 6120 apresenta uma sÈrie de valores que podem ser assumidos para as
cargas acidentais que venham a constituir carregamento em lajes. Alguns valores s„o
reproduzidos a seguir:
arquibancadas .......................................................................................................... 4,0 kN/m2
bibliotecas
sala de leitura .................................................................................................. 2,5 kN/m2
sala para depÛsito de livros ............................................................................ 4,0 kN/m2
sala com estantes ........................................................................................... 6,0 kN/m2
cinemas
platÈia com assentos fixos .............................................................................. 3,0 kN/m2
est˙dio e platÈia com assentos mÛveis .......................................................... 4,0 kN/m2
banheiro .......................................................................................................... 2,0 kN/m2
corredores
com acesso ao p˙blico .................................................................................... 3,0 kN/m2
sem acesso ao p˙blico .................................................................................... 2,0 kN/m2
edifÌcios residenciais
dormitÛrio, sala, copa, cozinha e banheiro ..................................................... 1,5 kN/m2
dispensa, ·rea de serviÁo e lavanderia ........................................................... 2,0 kN/m2
escadas
com acesso ao p˙blico .................................................................................... 3,0 kN/m2
sem acesso ao p˙blico .................................................................................... 2,5 kN/m2
escolas
anfiteatro, corredor e sala de aula .................................................................. 3,0 kN/m2
outras salas ..................................................................................................... 2,0 kN/m2
escritÛrios ................................................................................................................. 2,0 kN/m2
forros sem acesso de pessoas ................................................................................. 0,5 kN/m2
gin·sio de esportes .................................................................................................. 5,0 kN/m2
hospitais
dormitÛrio, enfermarias, sala de recuperaÁ„o ou cirurgia, banheiro ............... 2,0 kN/m2
corredor ........................................................................................................... 3,0 kN/m2
lojas .......................................................................................................................... 4,0 kN/m2
restaurantes ............................................................................................................. 3,0 kN/m2
teatros
palco ............................................................................................................... 5,0 kN/m2
platÈia com assentos fixos .............................................................................. 3,0 kN/m2
est˙dio e platÈia com assentos mÛveis .......................................................... 4,0 kN/m2
banheiro .......................................................................................................... 2,0 kN/m2

7. 2006 8-7 ufpr/tc405
Exemplo 8.1: Determinar o carregamento em uma laje de edifÌcio comercial. A laje ter· de 10 cm
de espessura, contra-piso (argamassa de cimento e areia) de 1 cm, acabamento
superior com tacos e acabamento inferior com forro de gesso com 1 cm de
espessura.
SoluÁ„o: As cargas permanentes (EquaÁ„o 8.2) e acidentais dever„o ser determinadas por
unidade de ·rea (kN/m2
). Os pesos do concreto armado, conta-piso e gesso
correspondem a 25 kN/m3
, 21 kN/m3
e 12,5 kN/m3
, respectivamente. Os tacos
pesam 0,65 kN/m2
. A carga acidental de um edifÌcio comercial deve ser
considerada como sendo 2 kN/m2
.
a. Dados ñ uniformizaÁ„o de unidades (kN e m)
3
armconc m/kN25=γ
3
pisocont m/kN21=γ
3
gesso m/kN5,12=γ
2
taco m/kN65,0g =
m10,0cm10h armconc ==
m01,0cm1h pisocont ==
m01,0cm1hgesso ==
2
comedif m/kN2q =
b. Carga permanente
pp: .................... 25,0 x 0,10 = 2,50 kN/m2
contra-piso: ...... 21,0 x 0,01 = 0,21 kN/m2
gesso: .............. 12,5 x 0,01 = 0,13 kN/m2
tacos: ................................... = 0,65 kN/m2
gk = 3,49 kN/m2
(≈ 3,50 kN/m2
)
c. Carga acidental
qk = 2,00 kN/m2
d. Carga total
gk = 3,50 kN/m2
qk = 2,00 kN/m2
pk = 5,50 kN/m2
8.6.3 Paredes
O peso das paredes depende do tipo de tijolo (maciÁo ou furado) e da espessura do reboco.
Este peso normalmente È apresentado por metro quadrado de parede (parede de 1 m de largura
por 1 m de altura), como mostrado na Figura 8.9.
O peso por unidade de ·rea de uma parede rebocada em ambas as faces pode ser
representado por:
rebrebtijtijpar e2ep γ+γ= EquaÁ„o 8.3
onde
ppar peso da parede por unidade de ·rea, geralmente em kN/m2
;
γtij peso especÌfico do tijolo, geralmente em kN/m3
;
etij espessura (menor dimens„o em planta) do tijolo, geralmente em m.
γreb peso especÌfico do reboco, geralmente em kN/m3
; e
ereb espessura do reboco, geralmente em m.
tacos
contra-piso (1 cm)
concreto armado (10 cm)
gesso (1 cm)

8. 2006 8-8 ufpr/tc405
Figura 8.9 ñ Carga de paredes
Para materiais componentes de parede, podem ser usados os seguintes valores:
tijolo de furado ........................................................................................................... 12 kN/m3
tijolo de maciÁo .......................................................................................................... 16 kN/m3
reboco ....................................................................................................................... 20 kN/m3
A Tabela 8.1 mostra alguns valores de peso de parede. Na Tabela foi considerado reboco
de 2,5 cm de espessura por face.
parede sem reboco parede com reboco
tijolo
(cm)
tijolo furado
(kN/m2
)
tijolo maciÁo
(kN/m2
)
parede
(cm)
tijolo furado
(kN/m2
)
tijolo maciÁo
(kN/m2
)
10 1,20 1,60 15 2,20 2,60
12 1,44 1,92 17 2,44 2,92
15 1,80 2,40 20 2,80 3,40
20 2,40 3,20 25 3,40 4,20
Tabela 8.1 ñ Pesos de paredes
8.6.3.1 Cargas de paredes em lajes de dupla curvatura
As cargas de paredes apoiadas em lajes de dupla curvatura (Figura 8.10) podem ser
consideradas como equivalentes a uma carga uniformemente distribuÌda em toda esta laje. Para
este caso, considera-se o peso total da parede e divide-se este valor pela ·rea total da laje, como
apresentado a seguir:
yx
parparpar
par
hp
g
ll
l
×
××
= EquaÁ„o 8.4
onde:
gpar carga uniformemente distribuÌda, devida ‡ parede, por unidade de ·rea, atuando em
toda laje, geralmente em kN/m2
;
ppar peso da parede por unidade de ·rea, geralmente em kN/m2
;
lpar largura da parede, geralmente em metro;
hpar altura da parede, geralmente em metro;
e
hpar
1 m
1 m
lpar

9. 2006 8-9 ufpr/tc405
lx menor dimens„o da laje, geralmente em metro; e
ly maior dimens„o da laje, geralmente em metro.
Figura 8.10 ñ Parede sobre laje de dupla curvatura
Exemplo 8.2: Determinar a carga das paredes atuantes na laje abaixo representada. A altura das
paredes corresponde a 2,7 m e s„o constituÌdas de tijolo furado de 10 cm, reboco
de 1,5 cm em cada face.
SoluÁ„o: O peso por metro quadrado de parede È determinado pela EquaÁ„o 8.3 e a carga
uniformemente distribuÌda sobre a laje È determinada pele EquaÁ„o 8.4.
a. Dados ñ uniformizaÁ„o de unidades (kN e m)
3
tij m/kN12=γ
3
reb m/kN20=γ
m10,0cm10etij ==
m015,0cm5,1ereb ==
m7,42,25,2par =+=l
m7,2hpar =
m5,3x =l
m0,6y =l
b. Curvatura da laje
curvaturadupla271,1
5,3
0,6
x
y
⇒<==
l
l
c. Peso por metro quadrado de parede
rebrebtijtijpar e2ep γ+γ=
( ) ( ) 2
par m/kN80,1015,020210,012p =××+×=
2,2m
3,5m
6,0 m
2,5 m
ly
lxlpar
gpar (kN por m2
de laje)

10. 2006 8-10 ufpr/tc405
d. Carga uniformemente distribuÌda na laje
yx
parparpar
par
hp
g
ll
l
×
××
=
2
par m/kN09,1
00,650,3
70,270,480,1
g =
×
××
=
8.6.3.2 Cargas de paredes em lajes de uma só curvatura
As cargas de paredes apoiadas em lajes de uma sÛ curvatura se situam em duas condiÁıes:
− paredes paralelas ao lado maior da laje;e
− paredes paralelas ao lado menor da laje.
A carga de parede paralela ao lado maior È considerada como uma carga linear
uniformemente distribuÌda ao longo de sua largura (Figura 8.11), cujo valor È dado por:
parparpar hpg ×= EquaÁ„o 8.5
onde:
gpar carga uniformemente distribuÌda, devida ‡ parede, por unidade de comprimento
(linear), atuando ao longo da largura da parede, geralmente em kN/m;
ppar peso da parede por unidade de ·rea, geralmente em kN/m2
; e
hpar altura da parede, geralmente em metro.
Figura 8.11 ñ Parede paralela ao lado maior da laje
A carga de parede paralela ao lado menor È considerada como uma carga uniformemente
distribuÌda na ·rea de dimensıes lx por 0,5 lx (Figura 8.12), cujo valor È dado por:
2
hp
g
x
x
parparpar
par
l
l
l
×
××
=
EquaÁ„o 8.6
onde:
gpar carga uniformemente distribuÌda, devida ‡ parede, por unidade de ·rea, atuando na
·rea de dimensıes lx por 0,5 lx, geralmente em kN/m2
;
ppar peso da parede por unidade de ·rea, geralmente em kN/m2
;
lpar largura da parede, geralmente em metro;
hpar altura da parede, geralmente em metro; e
lx menor dimens„o da laje, geralmente em metro.
lx
lylpar
gpar (kN por metro de laje)

11. 2006 8-11 ufpr/tc405
Figura 8.12 ñ Parede paralela ao lado menor da laje
Exemplo 8.3: Determinar a carga das paredes atuantes nas lajes abaixo representadas. A altura
das paredes corresponde a 2,7 m e s„o constituÌdas de tijolo furado de 12 cm,
reboco de 1,5 cm em cada face.
SoluÁ„o: O peso por metro quadrado de parede È determinado pela EquaÁ„o 8.3. A carga
linear uniformemente distribuÌda sobre a laje L1 È determinada pela EquaÁ„o 8.5 e
a carga uniformemente distribuÌda na regi„o lx por 0,5 lx da laje L2 È determinada
pela EquaÁ„o 8.6.
a. Dados ñ uniformizaÁ„o de unidades (kN e m)
3
tij m/kN12=γ
3
reb m/kN20=γ
m12,0cm12etij ==
m015,0cm5,1ereb ==
m2,2par1 =l
m7,1par2 =l
m7,2hh 2parpar1 ==
2
xl
ly
lx
gpar (kN por m2
de laje)
lpar
1,6 m
2,5 m
6 m
2,4 m
2,2m
L1
3,6 m
6 m
2,4 m
1,7 m
L2

12. 2006 8-12 ufpr/tc405
m4,2x2x1 == ll
m0,6y2y1 == ll
b. Curvatura da laje
curvaturasÛuma250,2
4,2
0,6
x
y
⇒>==
l
l
c. Peso por metro quadrado de parede
rebrebtijtijpar e2ep γ+γ=
( ) ( ) 2
par m/kN04,2015,020212,012p =××+×=
d. Laje L1 - peso por metro linear de parede
parparpar hpg ×=
m/kN51,570,204,2gpar =×=
e. Laje L2 ñ peso por metro quadrado de parede
2
hp
g
x
x
parparpar
par
l
l
l
×
××
=
2
par m/kN25,3
2
40,2
40,2
70,270,104,2
g =
×
××
=
f. Carregamentos
8.6.4 Parapeitos e balcões
Ao longo dos parapeitos e balcıes devem ser consideradas aplicadas, uma carga horizontal
de 0,8 kN/m na altura do corrim„o e
uma carga vertical mÌnima de
2 kN/m (ABNT NBR 6120, item
2.2.15), como mostrado na
Figura 8.13.
Figura 8.13 ñ Parapeitos e balcıes
2 kN/m 0,8 kN/m
1,6 m
2,5 m
6 m
2,4 m
2,2m
L1
5,51 kN/m
L2
1,2 m
6 m
2,4 m
3,25 kN/m2
1,7 m
3 m

13. 2006 8-13 ufpr/tc405
8.6.5 Redução de cargas acidentais em pilares e fundações
No c·lculo dos pilares e das fundaÁıes de edifÌcios para escritÛrios, residÍncias e casas
comerciais n„o destinadas a depÛsitos, as cargas acidentais podem ser reduzidas de acordo com
os valores indicados na Tabela 8.2 (ABNT NBR 6120, item 2.2.1.8).
Nm de pisos que atuam
sobre o elemento
ReduÁ„o percentual das
cargas acidentais
1, 2 e 3 0%
4 20%
5 40%
6 ou mais 60%
Tabela 8.2 ñ ReduÁ„o de cargas acidentais
Na aplicaÁ„o da Tabela 8.2, o forro deve ser considerado como piso (Figura 8.14).
Figura 8.14 - ReduÁ„o de cargas
acidentais
8.7 Determinação de esforços em lajes
Para a determinaÁ„o dos esforÁos em lajes maciÁas de concreto armado, duas
simplificaÁıes s„o admitidas:
− existe uma separaÁ„o virtual entre as lajes e as vigas que suportam o painel de lajes;
e
− a reaÁ„o de apoio das vigas suporte do painel de lajes se faz de forma uniformemente
distribuÌda.
Embora concretadas de forma monolÌtica, admite-se que as lajes e vigas sejam separadas
virtualmente, de tal forma que possam ser projetadas individualmente (Figura 8.15). As vigas
suporte das lajes s„o consideradas como apoios indesloc·veis.
g + 1,0 q
g + 1,0 q
g + 1,0 q
g + 0,8 q
g + 0,6 q
g + 0,4 q
g + 0,4 q
g + 0,4 q
2m
1m (cob)
3m
4m
5m
6m
7m
im

14. 2006 8-14 ufpr/tc405
Figura 8.15 ñ SeparaÁ„o virtual entre lajes e vigas
Uma vez que as vigas suportes das lajes s„o consideradas como indesloc·veis, pode-se
admitir que as reaÁıes de apoio existentes nas interfaces lajes/vigas sejam consideradas como
uniformemente distribuÌdas (Figura 8.16). Rigorosamente isto n„o ocorre pois existe uma
tendÍncia de levantamento nos cantos das lajes.
Figura 8.16 ñ ReaÁ„o de apoio de lajes
8.7.1 Lajes isoladas
A determinaÁ„o dos esforÁos em lajes isoladas pode ser feita por processos aproximados
(MARCUS), pela teoria das placas (BARES), pela teoria das
charneiras pl·sticas (LANGENDONCK), etc.. Dentre o
conjunto de soluÁıes apresentadas na literatura mundial,
destacam-se as tabelas de CZERNY, para determinaÁ„o dos
momentos fletores atuantes em lajes isoladas. A notaÁ„o a
ser usada para CZERNY est· mostrada na Figura 8.17 e o
conjunto de tabelas È apresentado em 8.11.
Figura 8.17 ñNotaÁ„o das tabelas
de CZERNY
As tabelas de CZERNY foram confeccionadas para varias condiÁıes de contorno e carga.
Os momentos fletores s„o dados pelas seguintes expressıes:
y
2
x
by
y
2
x
y
x
2
x
bx
x
2
x
x
p
m
p
m
p
m
p
m
β
=
α
=
β
=
α
=
ll
ll
EquaÁ„o 8.7
lx
mby
ly
mbx
my
mx

15. 2006 8-15 ufpr/tc405
onde:
lx menor v„o;
ly maior v„o;
mx momento fletor positivo na direÁ„o x;
my momento fletor positivo na direÁ„o y;
mbx momento fletor negativo (borda) na direÁ„o x;
mby momento fletor negativo (borda) na direÁ„o y;
p carga uniformemente distribuÌda em toda laje;
αx coeficiente para definiÁ„o do momento fletor positivo na direÁ„o x;
αy coeficiente para definiÁ„o do momento fletor positivo na direÁ„o y;
βx coeficiente para definiÁ„o do momento fletor negativo (borda) na direÁ„o x; e
βy coeficiente para definiÁ„o do momento fletor negativo (borda) na direÁ„o y.
Se a carga uniformemente distribuÌda corresponder a um valor caracterÌstico (pk = gk + qk) os
momentos fletores resultar„o caracterÌsticos (mk). Se a carga corresponder a um valor de c·lculo
(pd = γg gk + γq qk), os momentos fletores resultar„o de c·lculo (md).
8.7.2 Lajes contínuas
Como as tabelas de CZERNY determinam momentos fletores isolados em bordas que s„o
contÌnuas em um painel de lajes,
torna-se necess·rio uniformizar estes
momentos negativos atuantes nestas
regiıes de continuidade de lajes
(Figura 8.18).
Figura 8.18 ñ Momentos fletores em lajes continuas
O momento negativo de borda, atuante na junÁ„o das lajes Li e Lj, È dado pela seguinte
express„o:
bibj
bj
bjbi
bij mm
m8,0
2
mm
maxm >







 +
= EquaÁ„o 8.8
A uniformizaÁ„o dos momentos fletores negativos atuantes na junÁ„o das lajes Li e Lj
implica em alteraÁıes (correÁıes) nos
momentos fletores positivos mi e mj
(Figura 8.19). O momento mi tem seu
valor reduzido ao passo que o
momento mj tem seu valor
aumentado.
Figura 8.19 ñMomentos fletores uniformizados em lajes
continuas
lxi
lyi
lyj
lxj
Li Lj
mi
mj
mbi mbj
lxi
lyi
lyj
lxj
Li Ljmbij mbj
mi,cor mj,cor

16. 2006 8-16 ufpr/tc405
O ajuste de momentos fletores positivos nas lajes Li e Lj corresponde a:
bibj
bijbj
jcor,j
icor,i
mm
2
mm
mm
mm
>
−
+=
=
EquaÁ„o 8.9
Como pode ser observado na EquaÁ„o 8.9, a correÁ„o de momentos positivos sÛ È feita
para o momento mj (momento que sofre acrÈscimo). Caso mbi seja maior que mbj, os Ìndices i e j
devem ser invertidos na EquaÁ„o 8.8 e na EquaÁ„o 8.9.
Deve ser observado tambÈm que na Figura 8.18 e na Figura 8.19, bem como na
EquaÁ„o 8.8 e na EquaÁ„o 8.9, os Ìndices x e y correspondentes as direÁıes das lajes Li e Lj n„o
foram considerados (aprecem na Figura 8.17). A relaÁ„o entre os valores apresentados sem os
Ìndices x e y (direÁıes) corresponde a:
mi myi momento fletor positivo na direÁ„o y da laje Li;
mj mxj momento fletor positivo na direÁ„o x da laje Lj;
mbi mbyi momento fletor negativo na direÁ„o y da laje Li; e
mbj mbxj momento fletor negativo na direÁ„o x da laje Lj.
Exemplo 8.4: Determinar os momentos fletores de c·lculo atuantes no painel de lajes abaixo
indicado. Considerar:
− estado limite ˙ltimo, combinaÁıes ˙ltimas normais, edificaÁ„o tipo 2 (γg = 1,4
e γq = 1,4);
− carga permanente uniformemente distribuÌda (gk): 4 kN/m2
: e
− carga acidental uniformemente distribuÌda (qk): 2 kN/m2
.
SoluÁ„o: A soluÁ„o do problema consiste na aplicaÁ„o da EquaÁ„o 8.7 para a determinaÁ„o
dos momentos fletores em lajes isoladas. A uniformizaÁ„o dos momentos negativos
nas regiıes de continuidade de lajes È feita com a utilizaÁ„o da EquaÁ„o 8.8. Para
a correÁ„o dos momentos positivos deve-se usar a EquaÁ„o 8.9.
a. Carregamento das lajes (valores de c·lculo)
qqkgd qgp γ+γ=
2
d m/kN4,80,24,10,44,1p =×+×=
b. Laje L1
m8,1x1 =l
m0,4y1 =l







=β
=β
=α
=α
⇒⇒==
00,12
00,8
20,40
20,14
tab22,2
8,1
0,4
1y
1x
1y
1x
x1
y1
l
l
4 m
1,2 m
5m3 m1,8 m
L1 L2 L3
L4
ly1 =
4 m
lx1 = 1,8 m
L1
mbx1
mx1
my1
mby1

17. 2006 8-17 ufpr/tc405
m/kNm92,1
20,14
8,14,8p
m
2
1x
2
1xd
d,1x =
×
=
α
=
l
m/kNm68,0
20,40
8,14,8p
m
2
1y
2
1xd
d,1y =
×
=
α
=
l
m/kNm40,3
00,8
8,14,8p
m
2
1x
2
1xd
d,1bx −=
×
−=
β
−=
l
m/kNm27,2
00,12
8,14,8p
m
2
1y
2
1xd
d,1by −=
×
−=
β
−=
l
c. Laje L2
m0,3x2 =l
m0,4y2 =l







=β
=β
=α
=α
⇒⇒==
50,17
00,13
83,47
87,27
tab33,1
0,3
0,4
2y
2x
2y
2x
x2
y2
l
l
m/kNm71,2
87,27
0,34,8p
m
2
2x
2
2xd
d,2x =
×
=
α
=
l
m/kNm58,1
83,47
0,34,8p
m
2
2y
2
2xd
d,2y =
×
=
α
=
l
m/kNm82,5
00,13
0,34,8p
m
2
2x
2
2xd
d,2bx −=
×
−=
β
−=
l
m/kNm32,4
50,17
0,34,8p
m
2
2y
2
2xd
d,2by −=
×
−=
β
−=
l
d. Laje L3
m0,4x3 =l
m0,5y3 =l







=β
=β
=α
=α
⇒⇒==
90,12
10,11
40,34
90,24
tab25,1
0,4
0,5
3y
3x
3y
3x
x3
y3
l
l
m/kNm40,5
90,24
0,44,8p
m
2
3x
2
3xd
d,3x =
×
=
α
=
l
m/kNm91,3
40,34
0,44,8p
m
2
3y
2
3xd
d,3y =
×
=
α
=
l
m/kNm11,12
10,11
0,44,8p
m
2
3x
2
3xd
d,3bx −=
×
−=
β
−=
l
m/kNm42,10
90,12
0,44,8p
m
2
3y
2
3xd
d,3by −=
×
−=
β
−=
l
e. Laje L4 (laje isost·tica ñ laje em balanÁo)
m2,1x4 =l
m/kNm05,6
2
2,14,8
2
p
m
22
4xd
d,4bx −=
×
−=−=
l
ly2 =
4 m
lx2 = 3 m
L2
mbx2
mx2
my2
mby2
lx3=
4 m
ly3 = 5 m
L3
mby3
my3
mbx3
mx3
lx4=
1,2 m
L4
mbx4

18. 2006 8-18 ufpr/tc405
f. UniformizaÁ„o de momentos fletores ñ Lajes L1/L2
d,1bd,2b
d,2b
d,2bd,1b
d,12b mm
m8,0
2
mm
maxm >







 +
=








×
+
=
82,58,0
2
82,540,3
maxm d,12b






=
66,4
61,4
maxm d,12b
m/kNm66,4m d,12b = ◄
d,1bd,2b
d,12bd,2b
d,2cor,d,2 mm
2
mm
mm >
−
+=
2
66,482,5
71,2m cor,d,2
−
+=
m/kNm29,3m cor,d,2 = ◄
g. UniformizaÁ„o de momentos fletores ñ Lajes L2/L3
d,2bd,3b
d,3b
d,3bd,2b
d,23b mm
m8,0
2
mm
maxm >







 +
=








×
+
=
42,108,0
2
42,1082,5
maxm d,23b






=
34,8
12,8
maxm d,23b
m/kNm34,8m d,23b = ◄
d,2bd,3b
d,23bd,3b
d,3cor,d,3 mm
2
mm
mm >
−
+=
2
34,842,10
91,3m cor,d,3
−
+=
m/kNm95,4m cor,d,3 = ◄
h. UniformizaÁ„o de momentos fletores ñ Lajes L1/L4
Como a laje L4 corresponde a um trecho isost·tico
(laje em balanÁo), obrigatoriamente o momento fletor
atuante na junÁ„o das lajes L1 e L4 È o da laje L4
(6,05 kNm/m).
N„o h· correÁ„o do momento positivo da laje L1
pois o momento da borda desta laje (2,27 kNm/m) È
inferior ao momento da borda da laje L4 (6,05 kNm/m).
m/kNm05,6mm d,4bd,14b == ◄
m/kNm68,0m d,1 = ◄
L1
3,40
1,92
L2
5,82
2,71
5,82
L1 L2
3,29
5,82
1,92
4,66
L2 L3
3,91
5,82 10,42
3,29
4,66
L2
3,29
L3
4,95
8,34
4,66
L1
L4
0,682,27
6,05
L1
L4
0,68
6,05

19. 2006 8-19 ufpr/tc405
i. UniformizaÁ„o de momentos fletores ñ Lajes L2/L4
Como a laje L4 corresponde a um
trecho isost·tico (laje em balanÁo),
obrigatoriamente o momento fletor atuante
na junÁ„o das lajes L2 e L4 È o da laje L4
(6,05 kNm/m).
N„o h· correÁ„o do momento positivo
da laje L2 pois o momento da borda desta
laje (4,32 kNm/m) È inferior ao momento da
borda da laje L4 (6,05 kNm/m).
m/kNm05,6mm d,4bd,24b == ◄
m/kNm58,1m d,2 = ◄
j. UniformizaÁ„o de momentos fletores ñ Lajes L3/L4
Como a laje L4 corresponde a um trecho isost·tico (laje em balanÁo), obrigatoriamente
o momento fletor atuante na junÁ„o das lajes L3 e L4 È o da laje L4 (6,05 kNm/m).
H· correÁ„o do momento positivo da laje L4 pois o momento da borda desta laje
(10,42 kNm/m) È superior ao momento da borda da laje L4 (6,05 kNm/m).
m/kNm05,6mm d,4bd,34b == ◄
d,4bd,3b
d,34bd,3b
d,4cor,d,4 mm
2
mm
mm >
−
+=
2
05,611,12
40,5m cor,d,4
−
+=
m/kNm43,8m cor,d,4 = ◄
k. Momentos fletores (kNm/m) na direÁ„o L1/L2/L3
L2
L4
1,58
4,326,05
L2
L4
1,58
6,05
L3
L4
5,40
12,11
6,05
L3
L4
8,43
6,05
L1 L2 L3
L4
1,92
3,29
4,95
4,66
8,34

20. 2006 8-20 ufpr/tc405
l. Momentos fletores (kNm/m) nas direÁıes L1/L4, L2/L4 e L3/L4
m. ObservaÁ„o
Embora a relaÁ„o entre o v„o maior (4 m) e o v„o menor (1,8 m) da laje L1 supere
dois, a dupla curvatura desta laje foi considerada.
Caso a curvatura na direÁ„o do v„o maior fosse desprezada (consideraÁ„o de laje
armada em uma sÛ direÁ„o), o resultado final praticamente n„o se alteraria pois o momento
fletor positivo na direÁ„o do balanÁo resultou bem prÛximo de zero (0,68 kNm/m) e o
momento fletor negativo (6,05 kNm/m) foi definido pela laje em balanÁo.
8.8 Armadura de flexão
8.8.1 Armadura principal e armadura secundária
Para as lajes armadas em duas direÁıes (curvatura em duas direÁıes ortogonais), todas as
armaduras de flex„o (armaduras longitudinais) s„o consideradas como principal.
Para as lajes armadas em uma sÛ direÁ„o (uma sÛ curvatura na direÁ„o do v„o menor), a
armadura considerada como
principal È aquela posicionada
na direÁ„o do v„o menor. Na
direÁ„o do v„o maior deve-se,
obrigatoriamente, colocar uma
armadura de distribuiÁ„o
denominada armadura
secund·ria (Figura 8.20).
Figura 8.20 ñ Armadura principal e secund·ria de lajes
L1 L2 L3
L4
6,05
6,05
6,05
0,68
8,43
1,58
lyly
lx lx
armadura principal
armadura secund·ria

21. 2006 8-21 ufpr/tc405
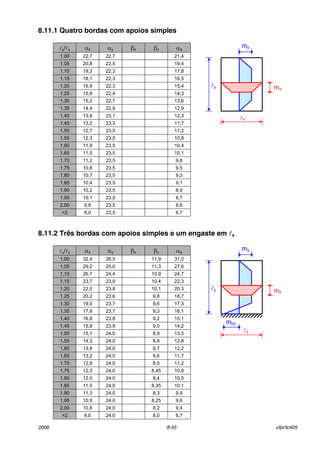
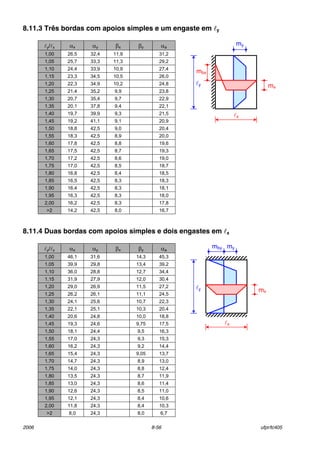
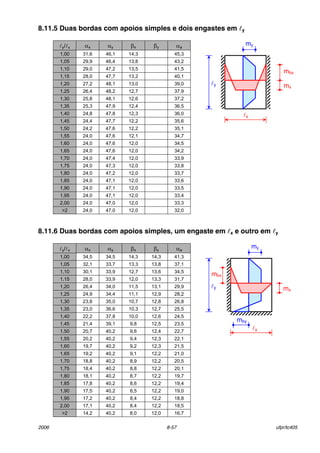
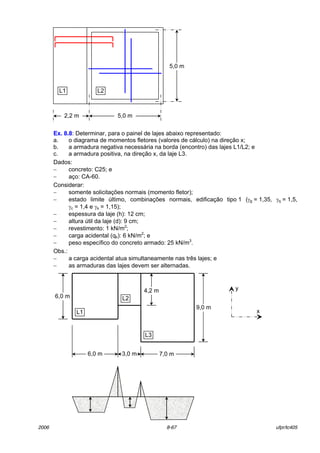
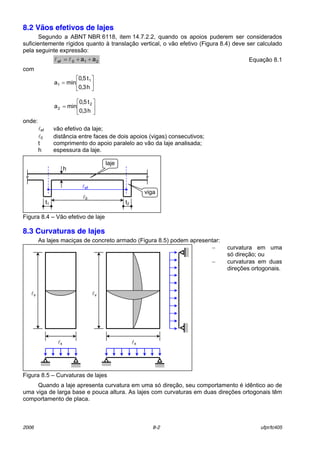
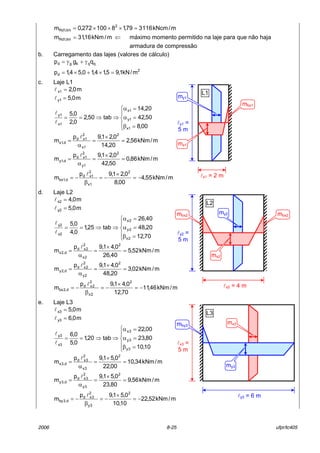
8.8.2 Equações gerais
Na determinaÁ„o da armadura de flex„o (momentos fletores) de lajes devem ser seguidos
os mesmos princÌpios estabelecidos no CapÌtulo [5]. A armadura ser· determinada para cada
metro de laje (bw = 1 m).
Para a determinaÁ„o da
altura ˙til È conveniente
adotar-se a altura ˙til da
armadura mais afastada da
borda tracionada
(Figura 8.21).
Figura 8.21 ñ SeÁ„o transversal de laje
( )lφ+−= 5,1chd nom EquaÁ„o 8.10
Para as lajes de pouca altura, as armaduras de compress„o devem ser evitadas. Desta
forma as equaÁıes para determinaÁ„o ou verificaÁ„o da armadura longitudinal de lajes
correspondem a:
x
yds
cdw
s
min,s
ydsz
1Rd
s
x
x
x
yd
s
x
s
xz
ck
ck
cd
2
w
1Rd
x
s
z
ck
ck
cd
2
w
1Rd
c
1RdRdSd
lim,1RdSd
w
ckcd
2
w
ckcd
2
w
lim,1Rd
fA
fdb68,0
A
fd
m
A
259,00,1â5,3
1
f
E
259,00,1
4,01
MPa35f400,0
MPa35f500,0
fdb272,0
m
5625,125,1
ou
tab
MPa35f228,0
MPa35f272,0
fdb
m
mmm
compress„odearmaduradeenecessidadh·n„omm
cm100b
MPa35ffdb228,0
MPa35ffdb272,0
m
β








=β
≥
ββ
=


















>β≤×





β
β−
≤β
=β
β−=β




>
≤
≤−−=β











β
β
⇒⇒
>
≤
≤=β
==
⇒≤
=




>
≤
=
EquaÁ„o 8.11
8.8.3 Armadura mínima
Os valores das armaduras mÌnimas para lajes maciÁas de concreto armado est„o
estabelecidos no item 19.3.3.3 da ABNT NBR 6118 e correspondem a:
− armadura negativa
c
yd
cd
min,s A
f
f
035,0A = (por metro de laje) EquaÁ„o 8.12
h d = h ñ (cnom + 1,5 φl)
bw = 100 cm
φl

22. 2006 8-22 ufpr/tc405
− armadura positiva de lajes armadas em duas direÁıes
c
yd
cd
min,s A
f
f
023,0A = (por metro de laje) EquaÁ„o 8.13
− armadura positiva (principal) de lajes armadas em uma direÁ„o
c
yd
cd
min,s A
f
f
035,0A = (por metro de laje) EquaÁ„o 8.14
− armadura positiva (secund·ria) de lajes armadas em uma direÁ„o














=
c
yd
cd
2
princ,s
min,s
A
f
f
018,0
cm9,0
A20,0
maxA (por metro de laje) EquaÁ„o 8.15
8.8.4 Diâmetro da armadura de flexão
Segundo o item 20.1 da ABNT NBR 6118, qualquer barra de armadura de flex„o de lajes
deve ter seu di‚metro limitado a 1/8 da
espessura da laje (Figura 8.22 e
EquaÁ„o 8.16).
Figura 8.22 ñ Di‚metro m·ximo da armadura de flex„o
8
h
≤φl EquaÁ„o 8.16
8.8.5 Espaçamento da armadura de flexão
ABNT NBR 6118, item 20.1
ìAs barras da armadura principal de flexão devem apresentar espaçamento no
máximo igual 2h ou 20 cm, prevalecendo o menor desses dois valores na região dos
maiores momentos fletores.
A armadura secundária de flexão deve ser igual ou superior a 20% da armadura
principal, mantendo-se, ainda, um espaçamento entre barras de, no máximo, 33 cm. A
emenda dessas barras deve respeitar os mesmos critérios de emenda das barras da
armadura principal.î
A Figura 8.23 mostra os espaÁamentos m·ximos da armadura de flex„o para lajes maciÁas
de concreto armado.
Figura 8.23 - EspaÁamento m·ximo da armadura de flex„o
h
φl
8
h
≤φl
φl
armadura principal










≤
h2
cm20
mins
armadura secund·ria
cm33s ≤

23. 2006 8-23 ufpr/tc405
Deve ser observado tambÈm que o item 20.1 da ABNT NBR 6118 n„o faz referÍncia ao
espaÁamento mÌnimo entre as barras de flex„o de lajes de concreto armado. Por razıes
construtivas, È conveniente n„o se posicionar barras com afastamentos inferiores a 7 cm.
De modo geral, pode-se estabelecer para as barras de flex„o de lajes de concreto armado:
− armadura principal






≤≤
h2
cm20
minscm7 EquaÁ„o 8.17
− armadura secund·ria
cm33scm10 ≤≤ EquaÁ„o 8.18
Observar que na EquaÁ„o 8.18 o espaÁamento mÌnimo para armadura secund·ria foi fixado
em 10 cm.
Exemplo 8.5: Determinar as armaduras necess·rias para o painel de lajes abaixo representada.
Dados:
− concreto: C25; e
− aÁo: CA-60.
Considerar:
− estado limite ˙ltimo, combinaÁıes ˙ltimas normais, edificaÁ„o tipo 2 (γg = 1,4
γq = 1,4, γc = 1,4 e γs = 1,15);
− espessura das lajes (h): 12 cm;
− cobrimento nominal (cnom): 2,5 cm;
− barras de flex„o n„o alternadas;
− carga permanente uniformemente distribuÌda (gk): 5 kN/m2
: e
− carga acidental uniformemente distribuÌda (qk): 1,5 kN/m2
.
SoluÁ„o: A soluÁ„o do problema consiste na aplicaÁ„o da EquaÁ„o 8.7 para a determinaÁ„o
dos momentos fletores em lajes isoladas. A uniformizaÁ„o dos momentos negativos
na regi„o de continuidade de lajes È feita com a utilizaÁ„o da EquaÁ„o 8.8. Para a
correÁ„o dos momentos positivos deve-se usar a EquaÁ„o 8.9. As armaduras
devem ser determinadas com a aplicaÁ„o da EquaÁ„o 8.10, EquaÁ„o 8.11,
EquaÁ„o 8.12, EquaÁ„o 8.13, EquaÁ„o 8.14, EquaÁ„o 8.15, EquaÁ„o 8.16,
EquaÁ„o 8.17 e EquaÁ„o 8.18.
a. Dados - uniformizaÁ„o de unidades (kN e cm)
2
ck kN/cm2,5MPa25f ==
normal)combinaÁ„o-(ELU1,40=γc
2
c
ck
cd kN/cm79,1
1,40
2,5f
f ==
γ
=
2
yk kN/cm60MPa600f ==
normal)combinaÁ„o-(ELU1,15=γs
5 m
6m4 m2 m
L1 L2 L3

24. 2006 8-24 ufpr/tc405
2
s
yk
yd kN/cm2,52
1,15
60f
f ==
γ
=
cm010bw =
cm12h =
cm5,2cnom =
( )lφ+−= 5,1chd nom
( ) cm80,15,15,212d =×+−= (assumido φl = 10 mm)
2
wc cm002112100hbA =×==
armadura negativa
c
yd
cd
min,s A
f
f
035,0A =
m/cm44,11200
2,52
79,1
035,0A 2
min,s =××=
armadura positiva de lajes armadas em duas direÁıes
c
yd
cd
min,s A
f
f
023,0A =
m/cm95,01200
2,52
79,1
023,0A 2
min,s =××=
armadura positiva (principal) de lajes armadas em uma direÁ„o
c
yd
cd
min,s A
f
f
035,0A =
m/cm44,11200
2,52
79,1
035,0A 2
min,s =××=
armadura positiva (secund·ria) de lajes armadas em uma direÁ„o














=
c
yd
cd
2
princ,s
min,s
A
f
f
018,0
cm9,0
A20,0
maxA














=××
=
m/cm74,01200
2,52
79,1
018,0
cm9,0
A20,0
maxA
2
2
princ,s
min,s






=
m/cm90,0
A20,0
maxA 2
princ,s
min,s
8
h
≤φl
mm5,12cm50,1
8
12
max, =φ⇒=≤φ ll






≤≤
h2
cm20
minscm7






=×
≤≤
cm24122
cm20
minscm7
cm20scm7 ≤≤ (armadura principal)
cm33scm10 ≤≤ (armadura secund·ria)
MPa35ffdb272,0m ckcd
2
wlim,1Rd ≤=

25. 2006 8-25 ufpr/tc405
m/kNcm116379,18100272,0m 2
lim,1Rd =×××=
m/kNm16,31m lim,1Rd = ⇐ m·ximo momento permitido na laje para que n„o haja
armadura de compress„o
b. Carregamento das lajes (valores de c·lculo)
qqkgd qgp γ+γ=
2
d m/kN1,95,14,10,54,1p =×+×=
c. Laje L1
m0,2x1 =l
m0,5y1 =l





=β
=α
=α
⇒⇒==
00,8
50,42
20,14
tab50,2
0,2
0,5
1x
1y
1x
x1
y1
l
l
m/kNm56,2
20,14
0,21,9p
m
2
1x
2
1xd
d,1x =
×
=
α
=
l
m/kNm86,0
50,42
0,21,9p
m
2
1y
2
1xd
d,1y =
×
=
α
=
l
m/kNm55,4
00,8
0,21,9p
m
2
1x
2
1xd
d,1bx −=
×
−=
β
−=
l
d. Laje L2
m0,4x2 =l
m0,5y2 =l





=β
=α
=α
⇒⇒==
70,12
20,48
40,26
tab25,1
0,4
0,5
2x
2y
2x
x2
y2
l
l
m/kNm52,5
40,26
0,41,9p
m
2
2x
2
2xd
d,2x =
×
=
α
=
l
m/kNm02,3
20,48
0,41,9p
m
2
2y
2
2xd
d,2y =
×
=
α
=
l
m/kNm46,11
70,12
0,41,9p
m
2
2x
2
2xd
d,2bx −=
×
−=
β
−=
l
e. Laje L3
m0,5x3 =l
m0,6y3 =l





=β
=α
=α
⇒⇒==
10,10
80,23
00,22
tab20,1
0,5
0,6
3y
3y
3x
x3
y3
l
l
m/kNm34,10
00,22
0,51,9p
m
2
3x
2
3xd
d,3x =
×
=
α
=
l
m/kNm56,9
80,23
0,51,9p
m
2
3y
2
3xd
d,3y =
×
=
α
=
l
m/kNm52,22
10,10
0,51,9p
m
2
3y
2
3xd
d,3by −=
×
−=
β
−=
l
ly1 =
5 m
lx1 = 2 m
L1
mbx1
mx1
my1
ly2 =
5 m
lx2 = 4 m
L2
mbx2
mx2
my2mbx2
lx3 =
5 m
ly3 = 6 m
L3
my3
mx3mby3

26. 2006 8-26 ufpr/tc405
f. UniformizaÁ„o de momentos fletores ñ Lajes L1/L2
d,1bd,2b
d,2b
d,2bd,1b
d,12b mm
m8,0
2
mm
maxm >







 +
=








×
+
=
46,118,0
2
46,1155,4
maxm d,12b






=
17,9
01,8
maxm d,12b
m/kNm17,9m d,12b =
d,1bd,2b
d,12bd,2b
d,2cor,d,2 mm
2
mm
mm >
−
+=
2
17,946,11
52,5m cor,d,2
−
+=
m/kNm67,6m cor,d,2 =
g. UniformizaÁ„o de momentos fletores ñ Lajes L2/L3
d,2bd,3b
d,3b
d,3bd,2b
d,23b mm
m8,0
2
mm
maxm >







 +
=








×
+
=
52,228,0
2
52,2246,11
maxm d,23b






=
02,18
99,16
maxm d,23b
m/kNm02,18m d,23b =
d,2bd,3b
d,23bd,3b
d,3cor,d,3 mm
2
mm
mm >
−
+=
2
02,1852,22
56,9m cor,d,3
−
+=
m/kNm81,11m cor,d,3 =
h. Momentos fletores (kNm/m) na direÁ„o L1/L2/L3
L1
2,56
L211,46
5,52
11,464,55
L1
2,56
L2
6,67
11,469,17
L2 L3
9,5622,529,17
6,67
11,46
L2 L3
11,8118,029,17
6,67
L2 L3
11,81
18,029,17
L1
2,56 6,67

27. 2006 8-27 ufpr/tc405
i. Momentos fletores (kNm/m) das lajes sem continuidades (L1, L2 e L3)
j. Armadura para os momentos fletores na direÁ„o L1/L2/L3
mSd = 2,56 kNm/m
{
compress„odearmaduradeenecessidadh·n„omm
m/kNm16,31
lim,1Rd
m/kNm56,2
Sd ⇒<
321
m/kNcm256mmm 1RdRdSd ===
MPa35f272,0
fdb
m
ck
cd
2
w
1Rd
c ≤≤=β
OK272,0022,0
79,18100
256
2c <=
××
=β



=β
=β
⇒⇒=β
000,1
987,0
022,0
s
z
tabela
c 321
min,s
ydsz
1Rd
s A
fd
m
A ≥
ββ
=
m/cm95,0A 2
min,s =
m/cm95,0m/cm62,0
2,52000,18987,0
256
A 22
s <=
×××
=
m/cm95,0A 2
s = ◄
cm20scm7 ≤≤
mSd = -9,17 kNm/m
{
compress„odearmaduradeenecessidadh·n„omm
m/kNm16,31
lim,1Rd
m/kNm17,9
Sd ⇒<
321
m/kNcm917mmm 1RdRdSd ===
OK272,0080,0
79,18100
917
2c <=
××
=β



=β
=β
⇒⇒=β
000,1
950,0
080,0
s
z
tabela
c 321
m/cm44,1A 2
min,s =
OKm/cm44,1m/cm31,2
2,52000,18950,0
917
A 22
s >=
×××
=
L1
0,86
L2
3,02
L3
10,34
φ
(mm)
As,bar
(cm2
)
s
(cm)
As,ef
(cm2
/m)
►5 0,196 ►20 0,98
s cm → 0,196 cm2
100 cm → 0,95 cm2

28. 2006 8-28 ufpr/tc405
m/cm31,2A 2
s = ◄
cm20scm7 ≤≤
mSd = 6,67 kNm/m
{
compress„odearmaduradeenecessidadh·n„omm
m/kNm16,31
lim,1Rd
m/kNm67,6
Sd ⇒<
321
m/kNcm667mmm 1RdRdSd ===
OK272,0058,0
79,18100
667
2c <=
××
=β



=β
=β
⇒⇒=β
000,1
964,0
058,0
s
z
tabela
c 321
m/cm95,0A 2
min,s =
OKm/cm95,0m/cm66,1
2,52000,18964,0
667
A 22
s >=
×××
=
m/cm66,1A 2
s = ◄
cm20scm7 ≤≤
mSd = -18,02 kNm/m
{
compress„odearmaduradeenecessidadh·n„omm
m/kNm16,31
lim,1Rd
m/kNm02,18
Sd ⇒<
321
m/kNcm1802mmm 1RdRdSd ===
OK272,0157,0
79,18100
1802
2c <=
××
=β



=β
=β
⇒⇒=β
000,1
897,0
157,0
s
z
tabela
c 321
m/cm44,1A 2
min,s =
OKm/cm44,1m/cm81,4
2,52000,18897,0
1802
A 22
s >=
×××
=
m/cm81,4A 2
s = ◄
cm20scm7 ≤≤
mSd = 11,81 kNm/m
{
compress„odearmaduradeenecessidadh·n„omm
m/kNm16,31
lim,1Rd
m/kNm81,11
Sd ⇒<
321
m/kNcm1181mmm 1RdRdSd ===
φ
(mm)
As,bar
(cm2
)
s
(cm)
As,ef
(cm2
/m)
5 0,196 8 2,45
►6 0,283 ►12 2,36
7 0,385 16 2,41
φ
(mm)
As,bar
(cm2
)
s
(cm)
As,ef
(cm2
/m)
►5 0,196 ►11 1,78
6 0,283 17 1,66
φ
(mm)
As,bar
(cm2
)
s
(cm)
As,ef
(cm2
/m)
►8 0,503 ►10 5,03
10 0,785 16 4,91
s cm → 0,196 cm2
100 cm → 2,31 cm2

29. 2006 8-29 ufpr/tc405
OK272,0103,0
79,18100
1181
2c <=
××
=β



=β
=β
⇒⇒=β
000,1
935,0
103,0
s
z
tabela
c 321
m/cm95,0A 2
min,s =
OKm/cm95,0m/cm02,3
2,52000,18935,0
1181
A 22
s >=
×××
=
m/cm02,3A 2
s = ◄
cm20scm7 ≤≤
k. Armadura para os momentos fletores na direÁ„o das lajes sem continuidades (L1, L2 e L3)
mSd = 0,86 kNm/m
{
compress„odearmaduradeenecessidadh·n„omm
m/kNm16,31
lim,1Rd
m/kNm86,0
Sd ⇒<
321
m/kNcm86mmm 1RdRdSd ===
OK272,0008,0
79,18100
86
2c <=
××
=β



=β
=β
⇒⇒=β
000,1
996,0
008,0
s
z
tabela
c 321
m/cm95,0A 2
min,s =
m/cm95,0m/cm21,0
2,52000,18996,0
86
A 22
s <=
×××
=
m/cm95,0A 2
s = ◄
cm20scm7 ≤≤
mSd = 3,02 kNm/m
{
compress„odearmaduradeenecessidadh·n„omm
m/kNm16,31
lim,1Rd
m/kNm02,3
Sd ⇒<
321
m/kNcm302mmm 1RdRdSd ===
OK272,0026,0
79,18100
302
2c <=
××
=β



=β
=β
⇒⇒=β
000,1
984,0
026,0
s
z
tabela
c 321
m/cm95,0A 2
min,s =
m/cm95,0m/cm73,0
2,52000,18984,0
302
A 22
s <=
×××
=
φ
(mm)
As,bar
(cm2
)
s
(cm)
As,ef
(cm2
/m)
►6 0,283 ►9 3,14
8 0,503 16 3,14
φ
(mm)
As,bar
(cm2
)
s
(cm)
As,ef
(cm2
/m)
►5 0,196 ►20 0,98

30. 2006 8-30 ufpr/tc405
m/cm95,0A 2
s = ◄
cm20scm7 ≤≤
mSd = 10,34 kNm/m
{
compress„odearmaduradeenecessidadh·n„omm
m/kNm16,31
lim,1Rd
m/kNm34,10
Sd ⇒<
321
m/kNcm1034mmm 1RdRdSd ===
OK272,0090,0
79,18100
1034
2c <=
××
=β



=β
=β
⇒⇒=β
000,1
944,0
090,0
s
z
tabela
c 321
m/cm95,0A 2
min,s =
OKm/cm95,0m/cm62,2
2,52000,18944,0
1034
A 22
s >=
×××
=
m/cm62,2A 2
s = ◄
cm20scm7 ≤≤
l. Armadura positiva
φ
(mm)
As,bar
(cm2
)
s
(cm)
As,ef
(cm2
/m)
►5 0,196 ►20 0,98
φ
(mm)
As,bar
(cm2
)
s
(cm)
As,ef
(cm2
/m)
5 0,196 7 2,80
►6 0,283 ►10 2,83
7 0,385 14 2,75
L1 L2
φ 5 mm @ 20 cm
L3
φ 5 mm @ 11 cm φ 6 mm @ 9 cm
φ 5 mm @ 20 cm φ 5 mm @ 20 cm φ 6 mm @ 10 cm

31. 2006 8-31 ufpr/tc405
m. Armadura negativa
n. ConsideraÁ„o da laje L1 com curvatura em uma sÛ direÁ„o
Embora a relaÁ„o entre o v„o maior (5 m) e o v„o menor (2 m) da laje L1 supere dois,
a dupla curvatura desta laje foi considerada, resultando na armadura mostrada no item m
(todas armaduras consideradas como principais).
Caso a curvatura na direÁ„o do v„o maior fosse desprezada (consideraÁ„o de laje
armada em uma sÛ direÁ„o), os momentos fletores da laje L1 resultariam:
m0,2x1 =l
m0,5y1 =l
0,250,2
0,2
0,5
x1
y1
>==
l
l
m/kNm56,2
2,14
0,21,9
2,14
p
m
22
1xd
d,1x =
×
==
l
m/kNm55,4
0,8
0,21,9
0,8
p
m
22
1xd
d,1bx −=
×
−=−=
l
Como n„o houve modificaÁıes nos momentos fletores na direÁ„o L1/L2, a distribuiÁ„o
de momentos e armadura nesta direÁ„o permanecer· inalterada para todo o painel de laje.
ly1 =
5 m
lx1 = 2 m
L1
mbx1
mx1
BA l
p
8
p
m
2
B
l
−=
2,14
p
m
2
AB
l
+=
L2 L3
11,81
18,029,17
L1
2,56 6,67
L1 L2
φ 6 mm @ 12 cm
L3
φ 8 mm @ 10 cm

32. 2006 8-32 ufpr/tc405
A ˙nica modificaÁ„o dever· ser feita para a laje L1, na direÁ„o do maior v„o (5 m),
onde n„o haver· momento positivo atuando e dever· ser posicionada apenas uma
armadura de distribuiÁ„o, funÁ„o do momento positivo na outra direÁ„o (2,56 kNm/m).
… importante observar que a armadura positiva para o momento fletor positivo da laje
L1 (2,56 kNm/m) resultou em 0,95 cm2
/m, correspondente ao valor de armadura mÌnima
para laje armada em duas direÁıes. Como agora a laje ser· armada em uma sÛ direÁ„o, o
valor da armadura mÌnima deve ser alterado para 1,44 cm2
/m (1 φ de 5 mm @ 13 cm). Para
a armadura de distribuiÁ„o, tem-se:










=
m/cm90,0
A20,0
maxA
2
princ,s
min,s
m/kNm56,2mm/cm44,1A Sd
2
princ,s ==









 =×
=
m/cm90,0
m/cm29,044,120,0
maxA
2
2
min,s
m/cm90,0A 2
min,s = ◄
cm33scm10 ≤≤
A distribuiÁ„o de armaduras do painel de lajes fica como a seguir indicado.
armadura positiva
φ
(mm)
As,bar
(cm2
)
s
(cm)
As,ef
(cm2
/m)
►5 0,196 ►21 0,93
6,3 0,312 33 0,95
L1 L2
3,02
L3
10,34
L1 L2
φ 5 mm @ 13 cm
L3
φ 5 mm @ 11 cm φ 6 mm @ 9 cm
φ 5 mm @ 21 cm φ 5 mm @ 20 cm φ 6 mm @ 10 cm

33. 2006 8-33 ufpr/tc405
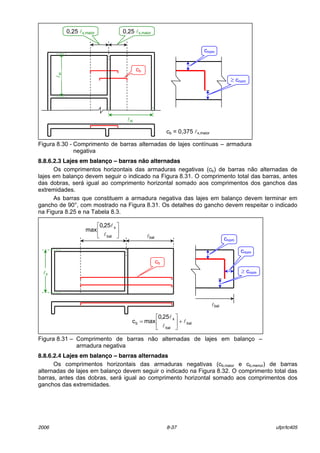
armadura negativa (inalterada)
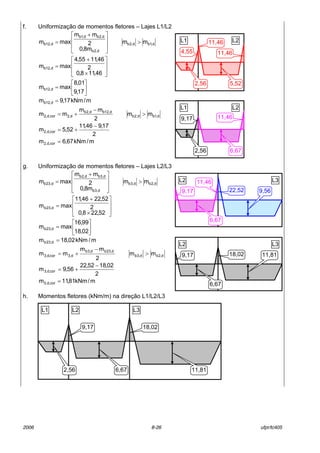
8.8.6 Comprimento de barras
8.8.6.1 Armadura positiva
8.8.6.1.1 Barras não alternadas
Os comprimentos horizontais das armaduras positivas (cbx e cby) de barras n„o alternadas
devem seguir o indicado na Figura 8.24. O comprimento total das barras, antes das dobras, ser·
igual ao comprimento horizontal somado aos comprimentos dos ganchos das extremidades.
Figura 8.24 ñ Comprimento de barras n„o alternadas ñ armadura positiva
Observar na Figura 8.24 que as barras que constituem a armadura positiva das lajes
maciÁas de concreto devem terminar em gancho. Isto deve ser feito para melhorar as condiÁıes
de ancoragem. O gancho de 90}, como mostrado na Figura 8.24, È o mais conveniente, embora
nem sempre possa ser usado. A ponta superior deste gancho deve, tambÈm, respeitar o
cobrimento nominal, o que nem sempre È possÌvel. Quando o gancho de 90m n„o puder ser
utilizado, pode-se fazer uso dos ganchos de 135} ou 180m, como mostrado na Figura [7.7] e na
Figura 8.25.
cby=l0y+bwy1+bwy2ñ2cnom-φl
bwy1bwy2
l0y
cbx = l0x + bwx1 + bwx2 ñ 2 cnom - φl
bwx2
l0x
bwx1
cbx
cby
bw
cnom
cnomφl
≥ cnom
L1 L2
φ 6 mm @ 12 cm
L3
φ 8 mm @ 10 cm

34. 2006 8-34 ufpr/tc405
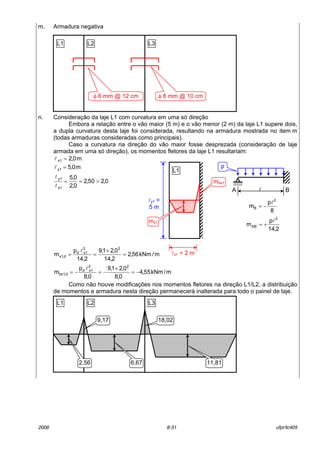
Figura 8.25 ñ Ganchos da armadura positiva
O di‚metro interno da curvatura (D) dos ganchos das armaduras longitudinais de traÁ„o
deve ser pelo menos igual ao estabelecido na Tabela [7.4] e na Tabela 8.3.
Tipo de AÁo
Bitola (mm)
CA-25 CA-50 CA-60
<20 4φ 5φ 6φ
≥20 5φ 8φ -
Tabela 8.3 ñ Di‚metro dos pinos de dobramento
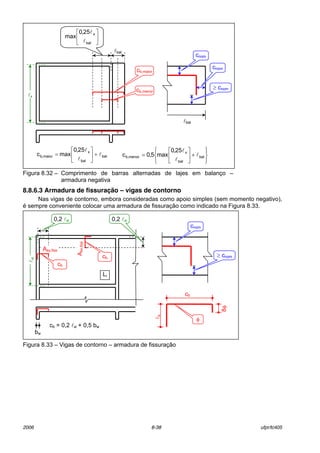
8.8.6.1.2 Barras alternadas
Os comprimentos horizontais das armaduras positivas (cbx e cby) de barras alternadas, para
lajes contÌnuas, devem seguir o indicado na Figura 8.26. O comprimento total das barras, antes
das dobras, ser· igual ao comprimento horizontal somado ao comprimento do gancho da
extremidade que chega ao apoio.
Figura 8.26 ñComprimento de barras alternadas ñ armadura positiva para lajes
contÌnuas
2φ
D φ
a)
4φ
D φ
b)
8φ
D φ
c)
cby=l0y+bwy1+bwy2-0,2lx
bwy1bwy2
l0y
cbx = l0x + bwx1 + bwx2 ñ 0,2 lx
bwx2
l0x
bwx1
cbx
cby
bw

35. 2006 8-35 ufpr/tc405
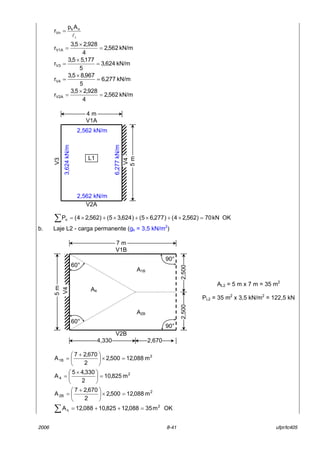
Os comprimentos horizontais das armaduras positivas (cbx e cby) de barras alternadas, para
lajes sem continuidade, devem seguir o indicado na Figura 8.27. O comprimento total das barras,
antes das dobras, ser· igual ao comprimento horizontal somado ao comprimento do gancho da
extremidade que chega ao apoio.
Figura 8.27 ñComprimento de barras alternadas ñ armadura positiva para
lajes sem continuidade
Para as lajes que apresentam continuidade em uma sÛ direÁ„o, os comprimentos
horizontais das armaduras positivas (cbx e cby) de barras alternadas, devem ser determinados de
tal forma que:
− na direÁ„o da continuidade, seja seguido o indicado na Figura 8.26; e
− na direÁ„o onde n„o existe continuidade, seja seguido o indicado na Figura 8.27.
… importante observar que a ABNT NBR 6118, item 20.1, n„o faz referÍncia aos
espaÁamentos m·ximo e mÌnimo da armadura de
flex„o de lajes maciÁas de concreto constituÌdas por
barras alternadas. Como o mÌnimo de trÍs barras por
metro de laje deve ser mantido, o espaÁamento
m·ximo das barras alternadas deve seguir o indicado
na Figura 8.28 {[3 bar x (2 x 17 cm )]= 102 cm ≈ 1 m}.
Figura 8.28 ñEspaÁamento m·ximo da
armadura de flex„o ñ barras
alternadas
armadura principal










≤
h2
cm17
mins
bw
cnom
cnomφl
≥ cnom
cby=l0y+bwy1+bwy2ñ0,1lx
bwy1bwy2
l0y
cbx = l0x + bwx1 + bwx2 ñ 0,1 lx
bwx2
l0x
bwx1
cbx
cby

36. 2006 8-36 ufpr/tc405
Quanto ao espaÁamento mÌnimo deve-se ser mantido o estabelecido na EquaÁ„o 8.17.
Desta forma, pode-se estabelecer para armadura de flex„o de lajes maciÁas de concreto
constituÌdas por barras alternadas:






≤≤
h2
cm17
minscm7 EquaÁ„o 8.19
8.8.6.2 Armadura negativa
8.8.6.2.1 – Lajes contínuas - barras não alternadas
Os comprimentos horizontais das armaduras negativas (cb) de barras n„o alternadas de
lajes contÌnuas devem seguir o indicado na Figura 8.29. O comprimento total das barras, antes
das dobras, ser· igual ao comprimento horizontal somado aos comprimentos dos ganchos das
extremidades.
Figura 8.29 - Comprimento de barras n„o alternadas de lajes contÌnuas ñ
armadura negativa
As barras que constituem a armadura negativa das lajes continuas devem terminar em
gancho de 90}, com mostrado na Figura 8.29. Os detalhes do gancho devem respeitar o indicado
na Figura 8.25 e na Tabela 8.3.
8.8.6.2.2 – Lajes contínuas - barras alternadas
Os comprimentos horizontais das armaduras negativas (cb) de barras alternadas de lajes
contÌnuas devem seguir o indicado na Figura 8.30. O comprimento total das barras, antes das
dobras, ser· igual ao comprimento horizontal somado aos comprimentos dos ganchos das
extremidades.
cb = 0,5 lx,maior
cb
lxi
lxk
0,25 lx,maior0,25 lx,maior
lxj
lxli
cnom
≥ cnom

37. 2006 8-37 ufpr/tc405
Figura 8.30 - Comprimento de barras alternadas de lajes contÌnuas ñ armadura
negativa
8.8.6.2.3 Lajes em balanço – barras não alternadas
Os comprimentos horizontais das armaduras negativas (cb) de barras n„o alternadas de
lajes em balanÁo devem seguir o indicado na Figura 8.31. O comprimento total das barras, antes
das dobras, ser· igual ao comprimento horizontal somado aos comprimentos dos ganchos das
extremidades.
As barras que constituem a armadura negativa das lajes em balanÁo devem terminar em
gancho de 90}, com mostrado na Figura 8.31. Os detalhes do gancho devem respeitar o indicado
na Figura 8.25 e na Tabela 8.3.
Figura 8.31 ñ Comprimento de barras n„o alternadas de lajes em balanÁo ñ
armadura negativa
8.8.6.2.4 Lajes em balanço – barras alternadas
Os comprimentos horizontais das armaduras negativas (cb,maior e cb,menor) de barras
alternadas de lajes em balanÁo devem seguir o indicado na Figura 8.32. O comprimento total das
barras, antes das dobras, ser· igual ao comprimento horizontal somado aos comprimentos dos
ganchos das extremidades.
cnom
cnom
lbal
≥ cnom






bal
x25,0
max
l
l
lbal
bal
bal
x
b
25,0
maxc l
l
l
+





=
cb
lx
cnom
≥ cnom
cb = 0,375 lx,maior
cb
lxi
0,25 lx,maior0,25 lx,maior
lxj

38. 2006 8-38 ufpr/tc405
Figura 8.32 ñ Comprimento de barras alternadas de lajes em balanÁo ñ
armadura negativa
8.8.6.3 Armadura de fissuração – vigas de contorno
Nas vigas de contorno, embora consideradas como apoio simples (sem momento negativo),
È sempre conveniente colocar uma armadura de fissuraÁ„o como indicado na Figura 8.33.
Figura 8.33 ñ Vigas de contorno ñ armadura de fissuraÁ„o
cnom
cnom
lbal
≥ cnom
lbal
bal
bal
x
maior,b
25,0
maxc l
l
l
+





=
cb,maior
lx






bal
x25,0
max
l
l
cb,menor








+





= bal
bal
x
menor,b
25,0
max5,0c l
l
l
cnom
≥ cnom
8φ
lb
cb
φ
bw
cb = 0,2 lxi + 0,5 bw
cb
lxi
0,2 lxi0,2 lxi
Li
cb
Asy,fiss
Asx,fiss

39. 2006 8-39 ufpr/tc405
A armadura de fissuraÁ„o, como mostrada na Figura 8.33, dever· corresponder a:














=
c
yd
cd
2
pos,sx
fiss,sx
A
f
f
018,0
cm9,0
A25,0
maxA (por metro de laje)














=
c
yd
cd
2
pos,sy
fiss,sy
A
f
f
018,0
cm9,0
A25,0
maxA (por metro de laje)
EquaÁ„o 8.20
8.9 Reações de apoio
Segundo a ABNT NBR 6118, item 14.7.6.1, as reaÁıes de apoio das lajes maciÁas
retangulares com carga uniformemente distribuÌda, em cada apoio, s„o as correspondentes ‡s
cargas atuantes nos tri‚ngulos ou trapÈzios determinados por retas inclinadas, a partir dos
vÈrtices com os seguintes ‚ngulos:
− 45} entre dois apoios do mesmo tipo;
− 60} a partir do apoio considerado engastado, se o outro for considerado simplesmente
apoiado; e
− 90} a partir do apoio, quando a borda vizinha for livre.
A Figura 8.34 mostra o esquema para c·lculo de reaÁıes de apoio de lajes.
Figura 8.34 − ReaÁıes de apoio de lajes
Para a viga Vn, sobre a qual as lajes mostradas na Figura 8.34 est„o apoiadas, a reaÁ„o de
apoio ser· dada por:
i
nk
Vn
Ap
r
l
= EquaÁ„o 8.21
onde:
rVn reaÁ„o de apoio na viga Vn;
pk valor caracterÌstico da carga uniformemente distribuÌda na laje;
An ·rea n definida pelo trapÈzio de base li da Figura 8.34;
li v„o da laje e da viga Vn, correspondente a base do trapÈzio da Figura 8.34.
A EquaÁ„o 8.21 È v·lida para qualquer trapÈzio ou tri‚ngulo mostrado na Figura 8.34. A
reaÁ„o de apoio em qualquer viga suporte das lajes mostradas na Figura ser· sempre dada pelo
produto da carga uniformemente distribuÌda pela ·rea do tri‚ngulo ou trapÈzio onde atua esta
carga, dividido pela base do trapÈzio ou tri‚ngulo (v„o da viga suporte).
60} 45}
60}45}
An
Vn
li
60}
90}
90}45}
An
Vn
li

40. 2006 8-40 ufpr/tc405
Exemplo 8.6: Determinar os esquemas de carregamento das vigas do painel abaixo
representado. Determinar, tambÈm, os carregamentos nos pilares.
Dados:
− carga permanente atuante nas lajes (peso prÛprio incluÌdo): 3,5 kN/m2
;
− carga acidental atuante nas lajes: 1,5 kN/m2
;
− paredes atuantes sobre as vigas de contorno (tijolo furado de 10 cm, reboco
de 1,5 cm e 2,5 m de altura): 4,5 kN/m; e
− peso prÛprio das vigas (20 cm x 50 cm): 2,5 kN/m.
SoluÁ„o: A soluÁ„o do problema consiste na determinaÁ„o, para as lajes, dos tri‚ngulos e
trapÈzios conforme o item 14.7.6.1 da ABNT NBR 6118. Os carregamentos sobre
as vigas s„o determinados pela aplicaÁ„o da EquaÁ„o 8.21. Os carregamentos nos
pilares s„o determinados pelo c·lculo das reaÁıes de apoio das vigas.
a. Laje L1 - carga permanente (gk = 3,5 kN/m2
)
2
1A m928,2
2
464,14
A =
×
=
2
3 m177,5464,1
2
072,25
A =×




 +
=
2
4 m967,8536,2
2
072,25
A =×




 +
=
2
2A m928,2
2
464,14
A =
×
=
OKm20928,2967,8177,5928,2A 2
n =+++=∑
1,464
5m
A1A
A2A
A3 A4
45}
45}
60}
60}
V4
V3
V2A
V1A
4 m
1,464
2,536
1,4642,072
AL1 = 4 m x 5 m = 20 m2
PL1 = 20 m2
x 3,5 kN/m2
= 70 kN
P1
P3 P4
P2
V4
V3
V2BV2A
V1BV1A
L1 L2
4 m 7 m
5 m

41. 2006 8-41 ufpr/tc405
i
nk
Vn
Ap
r
l
=
kN/m562,2
4
928,25,3
rV1A =
×
=
kN/m624,3
5
177,55,3
rV3 =
×
=
kN/m277,6
5
967,85,3
rV4 =
×
=
kN/m562,2
4
928,25,3
rV2A =
×
=
OKkN70)562,24()277,65()624,35()562,24(Pn =×+×+×+×=∑
b. Laje L2 - carga permanente (gk = 3,5 kN/m2
)
2
1B m088,12500,2
2
670,27
A =×




 +
=
2
4 m825,10
2
330,45
A =




 ×
=
2
2B m088,12500,2
2
670,27
A =×




 +
=
OKm35088,12825,10088,12A 2
n =++=∑
5m2,562 kN/m
2,562 kN/m
3,624kN/m
6,277kN/m
V4
V3
V2A
V1A
4 m
L1
AL2 = 5 m x 7 m = 35 m2
PL2 = 35 m2
x 3,5 kN/m2
= 122,5 kN
4,330
5m
A1B
A2B
A4
60}
60}
90}
90}
V4
V2B
V1B
7 m
2,500
2,670
2,500

42. 2006 8-42 ufpr/tc405
i
nk
Vn
Ap
r
l
=
kN/m044,6
7
088,125,3
rV1B =
×
=
kN/m578,7
5
825,105,3
rV4 =
×
=
kN/m044,6
7
088,125,3
rV2B =
×
=
OKkN5,122)044,67()578,75()044,67(Pn =×+×+×=∑
c. Painel de lajes - carga permanente (gk = 3,5 kN/m2
)
5m
V4
V2B
V1B
7 m
6,044 kN/m
6,044 kN/m
7,578kN/m
06,277kN/m
07,578kN/m
13,855kN/m
P1
P3 P4
P2
V4
V3
V2BV2A
V1BV1A
L1 L2
4 m 7 m
5 m
2,562 kN/m
3,624kN/m
2,562 kN/m
6,044 kN/m
6,044 kN/m

43. 2006 8-43 ufpr/tc405
d. Painel de lajes - carga acidental (qk = 1,5 kN/m2
)
Os procedimentos para a obtenÁ„o dos valores mostrados no painel de carga
acidental s„o os mesmos efetuados para o painel de cargas permanentes (itens a, b e c).
Trocou-se a carga permanente (gk = 3,5 kN/m2
) pela carga acidental (qk = 1,5 kN/m2
). Como
n„o h· variaÁ„o de cargas de uma laje para a outra, o painel mostrado neste item foi obtido
do painel mostrado no item c, na proporÁ„o 1,5/3,5 (carga acidental / carga permanente).
e. V3 ñ carregamento e reaÁıes de apoio
carga acidental: qk = 1,553 kN/m
carga permanente:
reaÁ„o da laje: 03,624 kN/m
parede: 04,500 kN/m
peso prÛprio da viga: 02,500 kN/m
gk = 10,624 kN/m
kN560,26
2
5624,10
GG 3P,kP1k, =
×
==
kN883,3
2
5553,1
QQ 3P,kP1k, =
×
==
f. V4 ñ carregamento e reaÁıes de apoio
carga acidental: qk = 5,938 kN/m
carga permanente:
reaÁ„o da laje: 13,855 kN/m
peso prÛprio da viga: 02,500 kN/m
gk = 16,355 kN/m
2,690kN/m
3,248kN/m
5,938kN/m
P1
P3 P4
P2
V4
V3
V2BV2A
V1BV1A
L1 L2
4 m 7 m
5 m
1,098 kN/m
1,553kN/m
1,098 kN/m
2,590 kN/m
2,590 kN/m
P3 P1
V3
5 m
qk = 1,553 kN/m
gk = 10,624 kN/m
Gk,P1 = 26,560 kN
Qk,P1 = 3,883 kN
Gk,P3
Qk,P3

44. 2006 8-44 ufpr/tc405
kN888,40
2
5355,16
GG 2V,kV1k, =
×
==
kN845,14
2
5938,5
QQ 2V,kV1k, =
×
==
g. V1 = V2 ñ carregamento e reaÁıes de apoio
V1A
carga acidental: qk = 1,098 kN/m
carga permanente:
reaÁ„o da laje: 02,562 kN/m
parede: 04,500 kN/m
peso prÛprio da viga: 02,500 kN/m
gk = 9,562 kN/m
V1B
carga acidental: qk = 2,590 kN/m
carga permanente:
reaÁ„o da laje: 06,044 kN/m
parede: 04,500 kN/m
peso prÛprio da viga: 02,500 kN/m
gk = 13,044 kN/m
kN926,112
11
7
888,40
11
5,3
7044,13
11
9
4562,9560,26GG 3P,kP1k, =





×+





××+





××+==
kN078,84
11
4
888,40
11
5,7
7044,13
11
2
4562,9GG 4P,kP2k, =





×+





××+





××==
kN692,22
11
7
845,14
11
5,3
7590,2
11
9
4098,1883,3QQ 3P,kP1k, =





×+





××+





××+==
V2 V1
V4
5 m
qk = 5,938 kN/m
gk = 16,355 kN/m
Gk,V1 = 40,888 kN
Qk,V1 = 14,845 kN
Gk,V2
Qk,V2
V1B
7 mP1 P2
V1A
4 m
Gk,P2 = 84,078 kN
Qk,P2 = 18,558 kN
Gk,P1 = 112,926 kN
Qk,P1 = 22,692 kN
qk = 2,590 kN/m
gk = 13,044 kN/m
qk = 1,098 kN/m
gk = 9,562 kN/m
Qk = 3,883 kN
Gk = 26,560 kN
Qk = 14,845 kN
Gk = 40,888 kN

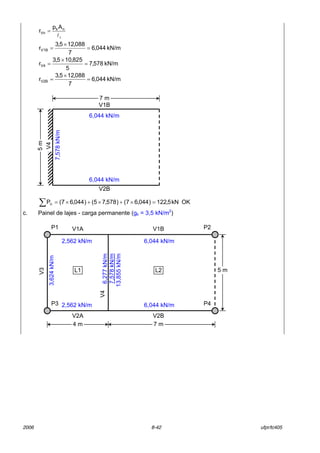
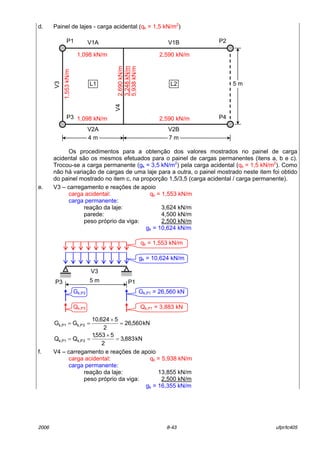
45. 2006 8-45 ufpr/tc405
kN558,18
11
4
845,14
11
5,7
7590,2
11
2
4098,1QQ 4P,kP2k, =





×+





××+





××==
h. VerificaÁ„o
carga permanente:
lajes: (20 m2
+ 35 m2
) x 3,5 kN/m2
................................ 192,5 kN
pp das vigas: [2 x (4 m + 7 m + 5 m)] x 2,5 kN/m ........... 80,0 kN
paredes: {[2 x (4 m + 7 m)] + 5 m} x 4,5 kN/m ............. 121,5 kN
total: .............................................................................. 394,0 kN
carga acidental:
lajes: (20 m2
+ 35 m2
) x 1,5 kN/m2
.................................. 82,5 kN
carga permanente (V1 + V2):
2 x (Gk,P1 + Gk,P2) = 2 x (112,926 + 84,078) .................. 394,0 kN
carga acidental (V1 + V2):
2 x (Qk,P1 + Qk,P2) = 2 x (22,692 + 18,558) ...................... 82,5 kN
i. ObservaÁ„o
Neste exemplo foram usados n˙meros com trÍs casas decimais, o que n„o È
necess·rio para c·lculos normais de estruturas de concreto. Este n˙mero exagerado de
casas decimais foi usado para demonstrar a precis„o da verificaÁ„o apresentada no item h.
8.10 Força cortante em lajes maciças de concreto armado
Segundo o item 19.4.1 da ABNT NBR 6118, as lajes maciÁas podem prescindir de armadura
transversal para resistir aos esforÁos de traÁ„o oriundos da forÁa cortante, quando a forÁa cortante
solicitante de c·lculo obedecer ‡ express„o1
:
1RdSd vv ≤ EquaÁ„o 8.22
onde:
vSd forÁa cortante solicitante de c·lculo (por metro de laje), podendo ser assumidas as
reaÁıes de apoio como mostrado em 8.9; e
vRd1 forÁa cortante resistente de c·lculo (por metro de laje).
A forÁa cortante resistente de c·lculo2
È dada por:
( )[ ]d402,1kv 1Rd1Rd ρ+τ= EquaÁ„o 8.23
onde:
τRd tens„o resistente de c·lculo ao cisalhamento;
k coeficiente funÁ„o da taxa de armadura existente na regi„o prÛxima ao apoio onde
est· sendo considerada a forÁa cortante;
ρ1 taxa de armadura existente na regi„o prÛxima ao apoio onde est· sendo considerada
a forÁa cortante; e
d altura ˙til da laje.
A tens„o resistente de c·lculo ao cisalhamento È dada por:
MPaemff
0525,0
ck
3 2
ck
c
Rd
γ
=τ EquaÁ„o 8.24
1
A ABNT NBR 6118 apresenta a equaÁ„o de verificaÁ„o de forÁa cortante como sendo VSd ≤ VRd1, ou seja,
verificaÁ„o de forÁas pontuais (kN). A EquaÁ„o 8.22 faz a verificaÁ„o de forÁas cortantes por unidade de
comprimento (kN/m).
2
A express„o apresentada pela ABNT NBR 6118 corresponde a ( )[ ] db15,0402,1kV wcp1Rd1Rd σ+ρ+τ= . Nesta
express„o est„o incluÌdos o valor de bw, para que a express„o resulte em forÁa pontual (kN), e o valor σcp, relativo ‡
forÁa de protens„o. A EquaÁ„o 8.23 n„o tem bw (resulta em forÁa cortante por unidade de comprimento - kN/m) e
n„o tem σcp (n„o considera forÁa de protens„o).
OK
OK

46. 2006 8-46 ufpr/tc405
O coeficiente k deve ser determinado da seguinte forma:
a. para elementos onde 50% da armadura inferior n„o chega atÈ o apoio:
0,1k = EquaÁ„o 8.25
b. para os demais casos:
metrosemd
0,1
d6,1
maxk 




 −
= EquaÁ„o 8.26
A taxa de armadura ρ1, na regi„o prÛxima ao apoio onde est· sendo considerada a forÁa
cortante, È dada pela express„o:














=ρ
%2
db
A
min
w
1s
1 EquaÁ„o 8.27
onde:
As1 ·rea da armadura de traÁ„o que se estende atÈ n„o menos de d + lb,nec alÈm da seÁ„o
considerada (Figura 8.35)1
;
bw largura mÌnima da seÁ„o ao longo da altura ˙til d (1 metro); e
d altura ˙til da laje.
Figura 8.35 ñ Armadura a ser considerada na verificaÁ„o de forÁa cortante em lajes
De modo geral pode-se adotar para valores de As1:
a. 100% da armadura principal que chega ao apoio onde est· sendo considerada a forÁa
cortante, para o caso de armadura n„o alternada; e
b. 50% da armadura principal que chega ao apoio onde est· sendo considerada a forÁa
cortante, para o caso de armadura alternada.
Exemplo 8.7: Verificar, para o painel abaixo representado, se as lajes podem prescindir de
armadura transversal para resistir aos esforÁos de traÁ„o oriundos da forÁa
cortante.
Dados:
− concreto: C25; e
− aÁo: CA-60.
Considerar:
- estado limite ˙ltimo, combinaÁıes ˙ltimas normais, edificaÁ„o tipo 2 (γg = 1,4
γq = 1,4, γc = 1,4 e γs = 1,15);
− espessura das lajes (h): 10 cm;
− cobrimento nominal (cnom): 2,5 cm;
− barras de flex„o alternadas;
− carga permanente atuante nas lajes (peso prÛprio incluÌdo): 3,5 kN/m2
; e
− carga acidental atuante nas lajes: 1,5 kN/m2
.
1
Alguns autores preferem considerar, sempre, a armadura positiva que chega ao apoio, ignorando as armaduras
tracionadas negativas.
d
seÁ„o
considerada
As
d + lb,nec
As1 d
seÁ„o
considerada
As
d + lb,nec
As1

47. 2006 8-47 ufpr/tc405
SoluÁ„o: A soluÁ„o do problema consiste na aplicaÁ„o da EquaÁ„o 8.7 para a determinaÁ„o
dos momentos fletores em lajes isoladas. A uniformizaÁ„o dos momentos negativos
na regi„o de continuidade de lajes È feita com a utilizaÁ„o da EquaÁ„o 8.8. Para a
correÁ„o dos momentos positivos deve-se usar a EquaÁ„o 8.9. As armaduras
devem ser determinadas com a aplicaÁ„o da EquaÁ„o 8.10 a EquaÁ„o 8.19. A
determinaÁ„o das reaÁıes de apoio das lajes (forÁa cortante) deve ser feita
conforme o item 14.7.6.1 da ABNT NBR 6118, com a aplicaÁ„o da EquaÁ„o 8.21. A
verificaÁ„o da forÁa cortante È feita com o uso da EquaÁ„o 8.22 a EquaÁ„o 8.27.
a. Dados - uniformizaÁ„o de unidades (kN e cm)
2
ck kN/cm2,5MPa25f ==
normal)combinaÁ„o-(ELU1,40=γc
2
c
ck
cd kN/cm79,1
1,40
2,5f
f ==
γ
=
2
yk kN/cm60MPa600f ==
normal)combinaÁ„o-(ELU1,15=γs
2
s
yk
yd kN/cm2,52
1,15
60f
f ==
γ
=
cm010bw =
cm10h =
cm5,2cnom =
( )lφ+−= 5,1chd nom
( ) cm3,68,05,15,210d =×+−= (assumido φl = 8 mm)
2
wc cm000110100hbA =×==
armadura negativa
c
yd
cd
min,s A
f
f
035,0A =
m/cm20,11000
2,52
79,1
035,0A 2
min,s =××=
armadura positiva de lajes armadas em duas direÁıes
c
yd
cd
min,s A
f
f
023,0A =
m/cm79,01000
2,52
79,1
023,0A 2
min,s =××=
P1
P3 P4
P2
V4
V3
V2BV2A
V1BV1A
L1 L2
4 m 4 m
5 m
V5

48. 2006 8-48 ufpr/tc405
armadura positiva (principal) de lajes armadas em uma direÁ„o
c
yd
cd
min,s A
f
f
035,0A =
m/cm20,11000
2,52
79,1
035,0A 2
min,s =××=
armadura positiva (secund·ria) de lajes armadas em uma direÁ„o














=
c
yd
cd
2
princ,s
min,s
A
f
f
018,0
cm9,0
A20,0
maxA














=××
=
m/cm62,01000
2,52
79,1
018,0
cm9,0
A20,0
maxA
2
2
princ,s
min,s






=
m/cm90,0
A20,0
maxA 2
princ,s
min,s
8
h
≤φl
mm5,12cm25,1
8
10
max, =φ⇒=≤φ ll






≤≤
h2
cm17
minscm7 (barras alternadas)






=×
≤≤
cm20102
cm17
minscm7
cm17scm7 ≤≤ (armadura principal, barras alternadas)
cm33scm10 ≤≤ (armadura secund·ria)
MPa35ffdb272,0m ckcd
2
wlim,1Rd ≤=
m/kNcm932179,13,6100272,0m 2
lim,1Rd =×××=
m/kNm32,19m lim,1Rd = ⇐ m·ximo momento permitido na laje para que n„o haja
armadura de compress„o
b. Carregamento das lajes (valores de c·lculo)
qqkgd qgp γ+γ=
2
d m/kN0,75,14,15,34,1p =×+×=
c. Laje L1
m0,4x1 =l
m0,5y1 =l





=β
=α
=α
⇒⇒==
9,9
2,35
4,21
tab25,1
0,4
0,5
1x
1y
1x
x1
y1
l
l
m/kNm23,5
4,21
0,40,7p
m
2
1x
2
1xd
d,1x =
×
=
α
=
l
m/kNm18,3
2,35
0,40,7p
m
2
1y
2
1xd
d,1y =
×
=
α
=
l
ly1=5m
lx1 = 4 m
L1
mbx1
mx1
my1

49. 2006 8-49 ufpr/tc405
m/kNm31,11
9,9
0,40,7p
m
2
1x
2
1xd
d,1bx −=
×
−=
β
−=
l
d. Momentos fletores das lajes com continuidade (L1/L2)
A uniformizaÁ„o de momentos È feita pela prÛpria simetria do painel de lajes.
e. Momentos fletores das lajes sem continuidades (L1 e L2)
f. Armadura para os momentos fletores
mSd = 5,23 kNm/m
{
compress„odearmaduradeenecessidadh·n„omm
m/kNm32,19
lim,1Rd
m/kNm23,5
Sd ⇒<
321
m/kNcm523mmm 1RdRdSd ===
MPa35f272,0
fdb
m
ck
cd
2
w
1Rd
c ≤≤=β
OK272,0074,0
79,13,6100
523
2c <=
××
=β



=β
=β
⇒⇒=β
000,1
954,0
074,0
s
z
tabela
c 321
min,s
ydsz
1Rd
s A
fd
m
A ≥
ββ
=
m/cm79,0A 2
min,s =
OKm/cm79,0m/cm67,1
2,52000,13,6954,0
523
A 22
s >=
×××
=
m/cm67,1A 2
s = ◄
L1
11,31 kN/m
5,23 kN/m
L2
5,23 kN/m
L1 L2
3,18kN/m
3,18kN/m

50. 2006 8-50 ufpr/tc405
cm17scm7 ≤≤
mSd = -11,31 kNm/m
{
compress„odearmaduradeenecessidadh·n„omm
m/kNm32,19
lim,1Rd
m/kNm31,11
Sd ⇒<
321
m/kNcm1131mmm 1RdRdSd ===
OK272,0159,0
79,13,6100
1131
2c <=
××
=β



=β
=β
⇒⇒=β
000,1
896,0
159,0
s
z
tabela
c 321
m/cm20,1A 2
min,s =
OKm/cm20,1m/cm84,3
2,52000,13,6896,0
1131
A 22
s >=
×××
=
m/cm84,3A 2
s = ◄
cm17scm7 ≤≤
mSd = 3,18 kNm/m
{
compress„odearmaduradeenecessidadh·n„omm
m/kNm32,19
lim,1Rd
m/kNm18,3
Sd ⇒<
321
m/kNcm318mmm 1RdRdSd ===
OK272,0045,0
79,13,6100
318
2c <=
××
=β



=β
=β
⇒⇒=β
000,1
973,0
045,0
s
z
tabela
c 321
m/cm79,0A 2
min,s =
OKm/cm79,0m/cm99,0
2,52000,13,6973,0
318
A 22
s >=
×××
=
m/cm99,0A 2
s = ◄
cm17scm7 ≤≤
φ
(mm)
As,bar
(cm2
)
s
(cm)
As,ef
(cm2
/m)
6 0,283 7 4,04
7 0,385 10 3,85
►8 0,503 ►13 3,87
s cm → 0,283 cm2
100 cm → 3,84 cm2
φ
(mm)
As,bar
(cm2
)
s
(cm)
As,ef
(cm2
/m)
►5 0,196 ►11 1,78
6 0,283 16 1,77
7 0,385 17 2,26
s cm → 0,196 cm2
100 cm → 1,67 cm2
φ
(mm)
As,bar
(cm2
)
s
(cm)
As,ef
(cm2
/m)
►5 0,196 ►17 1,15
6 0,283 17 1,66

51. 2006 8-51 ufpr/tc405
g. Armadura
h. ReaÁ„o de apoio - laje L1 - carga permanente (gk = 3,5 kN/m2
) - valores caracterÌsticos
2
1A m928,2
2
464,14
A =
×
=
2
3 m177,5464,1
2
072,25
A =×




 +
=
2
4 m967,8536,2
2
072,25
A =×




 +
=
2
2A m928,2
2
464,14
A =
×
=
OKm20928,2967,8177,5928,2A 2
n =+++=∑
i
nk
Vn
Ap
r
l
=
kN/m562,2
4
928,25,3
rV1A =
×
=
kN/m624,3
5
177,55,3
rV3 =
×
=
kN/m277,6
5
967,85,3
rV4 =
×
=
kN/m562,2
4
928,25,3
rV2A =
×
=
1,464
5m
A1A
A2A
A3 A4
45}
45}
60}
60}
V4
V3
V2A
V1A
4 m
1,464
2,536
1,4642,072
AL1 = 4 m x 5 m = 20 m2
PL1 = 20 m2
x 3,5 kN/m2
= 70 kN
L1 L2 φ 5 mm @ 17 cm
1,15 cm2
/m
φ 5 mm @ 11 cm
1,78 cm2
/m
φ 8 mm @ 13 cm
3,87 cm2
/m

52. 2006 8-52 ufpr/tc405
OKkN70)562,24()277,65()624,35()562,24(Pn =×+×+×+×=∑
i. Painel de lajes - carga permanente (gk = 3,5 kN/m2
) - valores caracterÌsticos
j. Painel de lajes - carga acidental (qk = 1,5 kN/m2
) ñ valores caracterÌsticos
Os procedimentos para a obtenÁ„o dos valores mostrados no painel de carga
acidental s„o os mesmos efetuados para o painel de cargas permanentes (itens h e i).
Trocou-se a carga permanente (gk = 3,5 kN/m2
) pela carga acidental (qk = 1,5 kN/m2
). Como
5m
2,562 kN/m
2,562 kN/m
3,624kN/m
6,277kN/m
V4
V3
V2A
V1A
4 m
L1
06,277kN/m
06,277kN/m
P1
P3 P4
P2
V4
V3
V2BV2A
V1BV1A
L1 L2
4 m 4 m
5 m
2,562 kN/m
3,624kN/m
2,562 kN/m
2,562 kN/m
2,562 kN/m
3,624kN/mV5
02,690kN/m
02,690kN/m
P1
P3 P4
P2
V4
V3
V2BV2A
V1BV1A
L1 L2
4 m 4 m
5 m
1,098 kN/m
1,553kN/m
1,098 kN/m
1,098 kN/m
1,098 kN/m
1,553kN/mV5

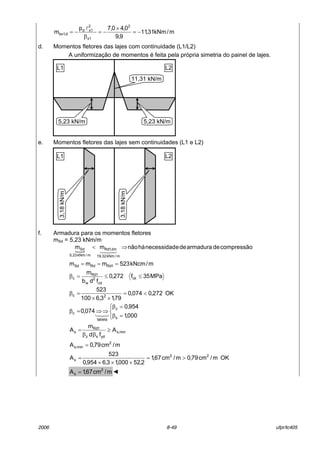
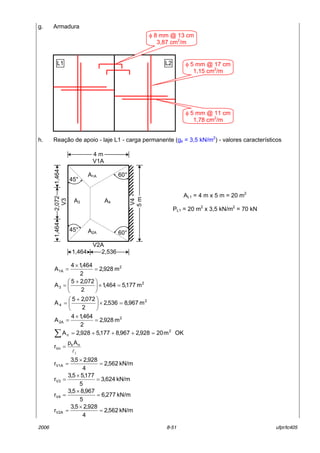
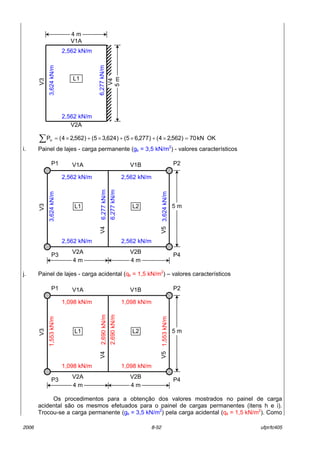
53. 2006 8-53 ufpr/tc405
n„o h· variaÁ„o de cargas de uma laje para a outra, o painel mostrado neste item foi obtido
do painel mostrado no item i, na proporÁ„o 1,5/3,5 (carga acidental / carga permanente).
k. Apoio V1A ñ verificaÁ„o da forÁa cortante (igual para V1B, V2A e V2B)
qkgkSd r4,1r4,1v +=
m/kN562,2r A1V,gk =
m/kN098,1r A1V,qk =
m/kN1,5098,14,1562,24,1vSd =×+×=
MPaemff
0525,0
ck
3 2
ck
c
Rd
γ
=τ
23 2
Rd cm/kN032,0MPa321,025
4,1
0525,0
===τ
0,1k = (barras alternadas)
2
A
A ef,s
1s = (barras alternadas)
m/cm15,1A 2
ef,s = (1 φ 5 mm @ 17 cm) ñ armadura positiva que chega na V1A














=ρ
%2
db
A
min
w
1s
1
%091,0
%2
%091,0
min
%2
3,6100
2
15,1
min1 =










=


















×
=ρ
( )[ ]d402,1kv 1Rd1Rd ρ+τ=
m/kN9,24cm/kN249,03,6
100
091,0
402,10,1032,0v 1Rd ==×











×+××=
1RdSd vv ≤
{ {
OKvv
m/kN9,24
1Rd
m/kN1,5
Sd <
l. Apoio V3 ñ verificaÁ„o da forÁa cortante (igual para V5)
m/kN624,3r 3V,gk =
m/kN553,1r 3V,qk =
m/kN2,7553,14,1624,34,1vSd =×+×=
2
Rd cm/kN032,0=τ
0,1k = (barras alternadas)
m/cm78,1A 2
ef,s = (1 φ 5 mm @ 11 cm) ñ armadura positiva que chega na V3 (V5)
%141,0
%2
%141,0
min
%2
3,6100
2
78,1
min1 =










=


















×
=ρ

54. 2006 8-54 ufpr/tc405
m/kN3,25cm/kN253,03,6
100
141,0
402,10,1032,0v 1Rd ==×











×+××=
{ {
OKvv
m/kN3,25
1Rd
m/kN2,7
Sd <
m. Apoio V4 ñ verificaÁ„o da forÁa cortante
m/kN277,6r 4V,gk =
m/kN690,2r 4V,qk =
m/kN6,12690,24,1277,64,1vSd =×+×=
2
Rd cm/kN032,0=τ
0,1k = (barras alternadas)
m/cm87,3A 2
ef,s = (1 φ 8 mm @ 13 cm) ñ armadura negativa sobre a V41
%307,0
%2
%307,0
min
%2
3,6100
2
87,3
min1 =










=


















×
=ρ
m/kN7,26cm/kN267,03,6
100
307,0
402,10,1032,0v 1Rd ==×











×+××=
{ {
OKvv
m/kN7,26
1Rd
m/kN6,12
Sd <
8.11 Tabelas de CZERNY
As tabelas as seguir apresentadas s„o v·lidas para lajes retangulares apoiadas em todas as
suas bordas, com carregamento uniformemente distribuÌdo. Estas tabelas apresentadas por
CZERNY no volume I do Beton Kalender de 1976 foram adaptadas por BURKE para coeficiente
de Poisson (ν) igual a 0,20.
Nas tabelas que se seguem valem as seguintes notaÁıes:
lx menor v„o da laje;
ly maior v„o da laje;
mx momento fletor positivo na direÁ„o x;
my momento fletor positivo na direÁ„o na y;
mbx momento fletor negativo (borda) na direÁ„o x;
mby momento fletor negativo (borda) na direÁ„o y;
a flecha m·xima da laje;
p carga uniformemente distribuÌda em toda laje;
αx coeficiente para definiÁ„o do momento fletor positivo na direÁ„o x;
αy coeficiente para definiÁ„o do momento fletor positivo na direÁ„o y;
βx coeficiente para definiÁ„o do momento fletor negativo (borda) na direÁ„o x;
βy coeficiente para definiÁ„o do momento fletor negativo (borda) na direÁ„o y;
αa coeficiente para definiÁ„o da flecha;
Ec mÛdulo de elasticidade secante do concreto (Ecs); e
h espessura da laje.
x
2
x
x
p
m
α
=
l
y
2
x
y
p
m
α
=
l
x
2
x
bx
p
m
β
−=
l
y
2
x
by
p
m
β
−=
l
a
3
c
4
x
hE
p
a
α
=
l
1
Alguns autores consideram as armaduras positivas que chegam ao apoio (1,78 cm
2
/m ñ 1 φ de 5 mm @ 11 cm).

55. 2006 8-55 ufpr/tc405
8.11.1 Quatro bordas com apoios simples
ly/lx αx αy βx βy αa
1,00 22,7 22,7 21,4
1,05 20,8 22,5 19,4
1,10 19,3 22,3 17,8
1,15 18,1 22,3 16,5
1,20 16,9 22,3 15,4
1,25 15,9 22,4 14,3
1,30 15,2 22,7 13,6
1,35 14,4 22,9 12,9
1,40 13,8 23,1 12,3
1,45 13,2 23,3 11,7
1,50 12,7 23,5 11,2
1,55 12,3 23,5 10,8
1,60 11,9 23,5 10,4
1,65 11,5 23,5 10,1
1,70 11,2 23,5 9,8
1,75 10,8 23,5 9,5
1,80 10,7 23,5 9,3
1,85 10,4 23,5 9,1
1,90 10,2 23,5 8,9
1,95 10,1 23,5 8,7
2,00 9,9 23,5 8,6
>2 8,0 23,5 6,7
8.11.2 Três bordas com apoios simples e um engaste em lx
ly/lx αx αy βx βy αa
1,00 32,4 26,5 11,9 31,2
1,05 29,2 25,0 11,3 27,6
1,10 26,1 24,4 10,9 24,7
1,15 23,7 23,9 10,4 22,3
1,20 22,0 23,8 10,1 20,3
1,25 20,2 23,6 9,8 18,7
1,30 19,0 23,7 9,6 17,3
1,35 17,8 23,7 9,3 16,1
1,40 16,8 23,8 9,2 15,1
1,45 15,8 23,9 9,0 14,2
1,50 15,1 24,0 8,9 13,5
1,55 14,3 24,0 8,8 12,8
1,60 13,8 24,0 8,7 12,2
1,65 13,2 24,0 8,6 11,7
1,70 12,8 24,0 8,5 11,2
1,75 12,3 24,0 8,45 10,8
1,80 12,0 24,0 8,4 10,5
1,85 11,5 24,0 8,35 10,1
1,90 11,3 24,0 8,3 9,9
1,95 10,9 24,0 8,25 9,6
2,00 10,8 24,0 8,2 9,4
>2 8,0 24,0 8,0 6,7
lx
ly
my
mx
mby
ly
my
mx
lx

56. 2006 8-56 ufpr/tc405
8.11.3 Três bordas com apoios simples e um engaste em ly
ly/lx αx αy βx βy αa
1,00 26,5 32,4 11,9 31,2
1,05 25,7 33,3 11,3 29,2
1,10 24,4 33,9 10,9 27,4
1,15 23,3 34,5 10,5 26,0
1,20 22,3 34,9 10,2 24,8
1,25 21,4 35,2 9,9 23,8
1,30 20,7 35,4 9,7 22,9
1,35 20,1 37,8 9,4 22,1
1,40 19,7 39,9 9,3 21,5
1,45 19,2 41,1 9,1 20,9
1,50 18,8 42,5 9,0 20,4
1,55 18,3 42,5 8,9 20,0
1,60 17,8 42,5 8,8 19,6
1,65 17,5 42,5 8,7 19,3
1,70 17,2 42,5 8,6 19,0
1,75 17,0 42,5 8,5 18,7
1,80 16,8 42,5 8,4 18,5
1,85 16,5 42,5 8,3 18,3
1,90 16,4 42,5 8,3 18,1
1,95 16,3 42,5 8,3 18,0
2,00 16,2 42,5 8,3 17,8
>2 14,2 42,5 8,0 16,7
8.11.4 Duas bordas com apoios simples e dois engastes em lx
ly/lx αx αy βx βy αa
1,00 46,1 31,6 14,3 45,3
1,05 39,9 29,8 13,4 39,2
1,10 36,0 28,8 12,7 34,4
1,15 31,9 27,9 12,0 30,4
1,20 29,0 26,9 11,5 27,2
1,25 26,2 26,1 11,1 24,5
1,30 24,1 25,6 10,7 22,3
1,35 22,1 25,1 10,3 20,4
1,40 20,6 24,8 10,0 18,8
1,45 19,3 24,6 9,75 17,5
1,50 18,1 24,4 9,5 16,3
1,55 17,0 24,3 9,3 15,3
1,60 16,2 24,3 9,2 14,4
1,65 15,4 24,3 9,05 13,7
1,70 14,7 24,3 8,9 13,0
1,75 14,0 24,3 8,8 12,4
1,80 13,5 24,3 8,7 11,9
1,85 13,0 24,3 8,6 11,4
1,90 12,6 24,3 8,5 11,0
1,95 12,1 24,3 8,4 10,6
2,00 11,8 24,3 8,4 10,3
>2 8,0 24,3 8,0 6,7
lx
ly
mbx
my
mx
ly
lx
mymby
mx

57. 2006 8-57 ufpr/tc405
8.11.5 Duas bordas com apoios simples e dois engastes em ly
ly/lx αx αy βx βy αa
1,00 31,6 46,1 14,3 45,3
1,05 29,9 46,4 13,8 43,2
1,10 29,0 47,2 13,5 41,5
1,15 28,0 47,7 13,2 40,1
1,20 27,2 48,1 13,0 39,0
1,25 26,4 48,2 12,7 37,9
1,30 25,8 48,1 12,6 37,2
1,35 25,3 47,9 12,4 36,5
1,40 24,8 47,8 12,3 36,0
1,45 24,4 47,7 12,2 35,6
1,50 24,2 47,6 12,2 35,1
1,55 24,0 47,6 12,1 34,7
1,60 24,0 47,6 12,0 34,5
1,65 24,0 47,6 12,0 34,2
1,70 24,0 47,4 12,0 33,9
1,75 24,0 47,3 12,0 33,8
1,80 24,0 47,2 12,0 33,7
1,85 24,0 47,1 12,0 33,6
1,90 24,0 47,1 12,0 33,5
1,95 24,0 47,1 12,0 33,4
2,00 24,0 47,0 12,0 33,3
>2 24,0 47,0 12,0 32,0
8.11.6 Duas bordas com apoios simples, um engaste em lx e outro em ly
ly/lx αx αy βx βy αa
1,00 34,5 34,5 14,3 14,3 41,3
1,05 32,1 33,7 13,3 13,8 37,1
1,10 30,1 33,9 12,7 13,6 34,5
1,15 28,0 33,9 12,0 13,3 31,7
1,20 26,4 34,0 11,5 13,1 29,9
1,25 24,9 34,4 11,1 12,9 28,2
1,30 23,8 35,0 10,7 12,8 26,8
1,35 23,0 36,6 10,3 12,7 25,5
1,40 22,2 37,8 10,0 12,6 24,5
1,45 21,4 39,1 9,8 12,5 23,5
1,50 20,7 40,2 9,6 12,4 22,7
1,55 20,2 40,2 9,4 12,3 22,1
1,60 19,7 40,2 9,2 12,3 21,5
1,65 19,2 40,2 9,1 12,2 21,0
1,70 18,8 40,2 8,9 12,2 20,5
1,75 18,4 40,2 8,8 12,2 20,1
1,80 18,1 40,2 8,7 12,2 19,7
1,85 17,8 40,2 8,6 12,2 19,4
1,90 17,5 40,2 8,5 12,2 19,0
1,95 17,2 40,2 8,4 12,2 18,8
2,00 17,1 40,2 8,4 12,2 18,5
>2 14,2 40,2 8,0 12,0 16,7
lx
ly
my
mx
mbx
lx
mby
ly
mbx
my
mx

58. 2006 8-58 ufpr/tc405
8.11.7 Três bordas engastadas e um apoio simples em lx
ly/lx αx αy βx βy αa
1,00 38,1 44,6 16,2 18,3 55,4
1,05 35,5 44,8 15,3 17,9 51,6
1,10 33,7 45,7 14,8 17,7 48,7
1,15 32,0 47,1 14,2 17,6 46,1
1,20 30,7 47,6 13,9 17,5 44,1
1,25 29,5 47,7 13,5 17,5 42,5
1,30 28,4 47,7 13,2 17,5 41,2
1,35 27,6 47,9 12,9 17,5 39,9
1,40 26,8 48,1 12,7 17,5 38,9
1,45 26,2 48,3 12,6 17,5 38,0
1,50 25,7 48,7 12,5 17,5 37,2
1,55 25,2 49,0 12,4 17,5 36,5
1,60 24,8 49,4 12,3 17,5 36,0
1,65 24,5 49,8 12,2 17,5 35,4
1,70 24,2 50,2 12,2 17,5 35,0
1,75 24,0 50,7 12,1 17,5 34,6
1,80 24,0 51,3 12,1 17,5 34,4
1,85 24,0 52,0 12,0 17,5 34,2
1,90 24,0 52,6 12,0 17,5 33,9
1,95 24,0 53,4 12,0 17,5 33,8
2,00 24,0 54,1 12,0 17,5 33,7
>2 24,0 54,0 12,0 17,5 32,0
8.11.8 Três bordas engastadas e um apoio simples em ly
ly/lx αx αy βx βy αa
1,00 44,6 38,1 18,3 16,2 55,4
1,05 41,7 37,3 16,6 15,4 49,1
1,10 38,1 36,7 15,4 14,8 44,1
1,15 34,9 36,4 14,4 14,3 40,1
1,20 32,1 36,2 13,5 13,9 36,7
1,25 29,8 36,1 12,7 13,5 33,8
1,30 28,0 36,2 12,2 13,3 31,7
1,35 26,4 36,6 11,6 13,1 29,7
1,40 25,2 37,0 11,2 13,0 28,1
1,45 24,0 37,5 10,9 12,8 26,6
1,50 23,1 38,3 10,6 12,7 25,5
1,55 22,3 39,3 10,3 12,6 24,5
1,60 21,7 40,3 10,1 12,6 23,6
1,65 21,1 41,4 9,9 12,5 22,8
1,70 20,4 42,7 9,7 12,5 22,1
1,75 20,0 43,8 9,5 12,4 21,5
1,80 19,5 44,8 9,4 12,4 21,0
1,85 19,1 45,9 9,2 12,3 20,5
1,90 18,7 46,7 9,0 12,3 20,1
1,95 18,4 47,7 8,9 12,3 19,7
2,00 18,0 48,6 8,8 12,3 19,3
>2 14,2 48,6 8,0 12,0 16,7
lx
mby
ly
mbx
my
mx
lx
mby
ly
mbx
my
mx

59. 2006 8-59 ufpr/tc405
8.11.9 Quatro bordas engastadas
ly/lx αx αy βx βy αa
1,00 47,3 47,3 19,4 19,4 68,5
1,05 43,1 47,3 18,2 18,8 62,4
1,10 40,0 47,8 17,1 18,4 57,6
1,15 37,3 48,3 16,3 18,1 53,4
1,20 35,2 49,3 15,5 17,9 50,3
1,25 33,4 50,5 14,9 17,7 47,6
1,30 31,8 51,7 14,5 17,6 45,3
1,35 30,7 53,3 14,0 17,5 43,4
1,40 29,6 54,8 13,7 17,5 42,0
1,45 28,6 56,4 13,4 17,5 40,5
1,50 27,8 57,3 13,2 17,5 39,5
1,55 27,2 57,6 13,0 17,5 38,4
1,60 26,6 57,8 12,8 17,5 37,6
1,65 26,1 57,9 12,7 17,5 36,9
1,70 25,5 57,8 12,5 17,5 36,3
1,75 25,1 57,7 12,4 17,5 35,8
1,80 24,8 57,6 12,3 17,5 35,4
1,85 24,5 57,5 12,2 17,5 35,1
1,90 24,2 57,4 12,1 17,5 34,7
1,95 24,0 57,2 12,0 17,5 33,8
2,00 24,0 57,1 12,0 17,5 34,5
>2 24,0 57,0 12,0 17,5 34,3
8.12 Simbologia específica
8.12.1 Símbolos base
a dimens„o
flecha
bw largura da laje
largura mÌnima da seÁ„o ao longo da altura ˙til d
bwxi largura da viga i na direÁ„o x
bwxj largura da viga j na direÁ„o x
bwyi largura da viga i na direÁ„o y
bwyj largura da viga j na direÁ„o y
cb comprimento horizontal de barra
cb,maior comprimento horizontal maior de barra
cb,menor comprimento horizontal menor de barra
cbx comprimento horizontal de barra na direÁ„o x
cby comprimento horizontal de barra na direÁ„o y
cnom cobrimento nominal
d altura ˙til da laje
ereb espessura do reboco
etij espessura (menor dimens„o em planta) do tijolo
fcd resistÍncia ‡ compress„o do concreto de c·lculo
fck resistÍncia ‡ compress„o do concreto caracterÌstica
fyd resistÍncia ao escoamento do aÁo de c·lculo
fyk resistÍncia ao escoamento do aÁo caracterÌstica
g carga permanente uniformemente distribuÌda
gk valor caracterÌstico da carga permanente
gpar carga uniformemente distribuÌda, devida ‡ parede, por unidade de ·rea
carga uniformemente distribuÌda, devida ‡ parede, por unidade de comprimento
gtaco peso do taco por metro quadrado
lx
mby
ly
mbx
my
mx

60. 2006 8-60 ufpr/tc405
h espessura da laje
espessura do material
hconc arm espessura do concreto armado
hcont piso espessura do contra-piso
hgesso espessura do gesso
hpar altura da parede
k coeficiente funÁ„o da taxa de armadura existente na regi„o prÛxima ao apoio
l v„o de laje
v„o de viga
lb comprimento de ancoragem
lb,nec comprimento de ancoragem necess·rio
lbal v„o de laje em balanÁo
lef v„o efetivo da laje
li v„o de laje
v„o de viga
lpar largura da parede
lx menor dimens„o da laje
lx,maior maior dos v„os lx
lxi menor dimens„o da laje Li
lxj menor dimens„o da laje Lj
ly maior dimens„o da laje
lyi maior dimens„o da laje Li
lyj maior dimens„o da laje Lj
l0 dist‚ncia entre faces de dois apoios (vigas) consecutivos
l0x dist‚ncia entre faces de dois apoios (vigas) consecutivos na direÁ„o x
l0y dist‚ncia entre faces de dois apoios (vigas) consecutivos na direÁ„o y
mbi momento fletor negativo (borda) da laje Li
mbi,d momento fletor negativo (borda) de c·lculo da laje Li
mbij momento fletor negativo (borda) na junÁ„o das lajes Li e Lj
mbij,d momento fletor negativo (borda) de c·lculo na junÁ„o das lajes Li e Lj
mbj momento fletor negativo (borda) da laje Lj
mbj,d momento fletor negativo (borda) de c·lculo da laje Lj
mbx momento fletor negativo (borda) na direÁ„o x
mbxi,d momento fletor negativo (borda) de c·lculo na direÁ„o x da laje Li
mby momento fletor negativo (borda) na direÁ„o y
mbyi,d momento fletor negativo (borda) de c·lculo na direÁ„o y da laje Li
mi momento fletor positivo da laje Li
mi,cor momento fletor positivo corrigido da laje Li
mi,d,cor momento fletor positivo corrigido de c·lculo da laje Li
mj momento fletor positivo da laje Lj
mj,cor momento fletor positivo corrigido da laje Lj
mx momento fletor positivo na direÁ„o x
mxi,d momento fletor positivo de c·lculo na direÁ„o x da laje Li
my momento fletor positivo na direÁ„o y
myi,d momento fletor positivo de c·lculo na direÁ„o y da laje Li
mAB momento fletor positivo no v„o AB
mB momento fletor negativo (engaste) no apoio B
mRd momento fletor resistente de c·lculo
mRd1 momento fletor resistente de c·lculo sem a consideraÁ„o de armadura comprimida
mRd1,lim momento fletor resistente de c·lculo corresponde ao limite de dutilidade da seÁ„o
mRd1,lim transversal (βx = βx,lim)
mSd momento fletor solicitante de c·lculo
p carga uniformemente distribuÌda correspondente ‡ somatÛria da carga permanente
mais a carga acidental
carga uniformemente distribuÌda na laje
carga uniformemente distribuÌda na viga

61. 2006 8-61 ufpr/tc405
pd valor de c·lculo da somatÛria carga permanente mais carga acidental
pk valor caracterÌstico da carga uniformemente distribuÌda na laje
valor caracterÌstico da somatÛria carga permanente mais carga acidental
ppar peso da parede por unidade de ·rea
peso da parede por unidade de ·rea
q carga acidental uniformemente distribuÌda
qedif com carga acidental de edifÌcios comerciais
qk valor caracterÌstico da carga acidental
rgk reaÁ„o de apoio caracterÌstica devida ‡ carga permanente
rgk,Vi reaÁ„o de apoio caracterÌstica devida ‡ carga permanente na viga Vi
rqk reaÁ„o de apoio caracterÌstica devida ‡ carga acidental
rqk,Vi reaÁ„o de apoio caracterÌstica devida ‡ carga acidental na viga Vi
rVn reaÁ„o de apoio na viga
s espaÁamento entre as barras que constituem a armadura longitudinal
t comprimento do apoio
vRd1 forÁa cortante resistente de c·lculo
vSd forÁa cortante solicitante de c·lculo
As1 ·rea da armadura de traÁ„o que se estende atÈ n„o menos de d + lb,nec alÈm da
seÁ„o considerada
Ac ·rea de concreto
An ·rea de tri‚ngulo ou trapÈzio
As ·rea da seÁ„o transversal da armadura longitudinal tracionada
As,bar ·rea da seÁ„o transversal da armadura longitudinal tracionada de uma barra
As,min ·rea da seÁ„o transversal mÌnima da armadura longitudinal tracionada
As,princ ·rea da seÁ„o transversal principal da armadura longitudinal tracionada
As,ef ·rea da seÁ„o transversal efetiva da armadura longitudinal tracionada
Asx,fiss armadura de fissuraÁ„o na direÁ„o x
Asx,pos armadura positiva na direÁ„o x
Asy,fiss armadura de fissuraÁ„o na direÁ„o y
Asy,pos armadura positiva na direÁ„o y
ALi ·rea da laje Li
D di‚metro interno da curvatura
Es mÛdulo de elasticidade do aÁo
Ec mÛdulo de elasticidade secante do concreto
Gk,Pi ReaÁ„o de apoio devida ‡ carga permanente no pilar Pi
Gk,Vi ReaÁ„o de apoio devida ‡ carga permanente na viga Vi
PLi forÁa resultante atuante na laje Li
Qk,Pi ReaÁ„o de apoio devida ‡ carga acidental no pilar Pi
Qk,Vi ReaÁ„o de apoio devida ‡ carga acidental na viga Vi
αa coeficiente para definiÁ„o da flecha
αx coeficiente para definiÁ„o do momento fletor positivo na direÁ„o x
αy coeficiente para definiÁ„o do momento fletor positivo na direÁ„o y
βc valor adimensional auxiliar
βs valor adimensional que define a tens„o de traÁ„o referente ‡ armadura As
βx coeficiente para definiÁ„o do momento fletor negativo (borda) na direÁ„o x
βx valor adimensional que define a posiÁ„o da linha neutra
βy coeficiente para definiÁ„o do momento fletor negativo (borda) na direÁ„o y
βz valor adimensional que define o braÁo de alavanca do bin·rio de forÁas Rcd1, Rsd1
φ di‚metro das barras da armadura
φl di‚metro da barra longitudinal
γc coeficiente de ponderaÁ„o da resistÍncia do concreto
γconc arm peso especÌfico do concreto armado
γcont piso peso especÌfico do contra-piso
γg coeficiente de ponderaÁ„o para aÁıes permanentes diretas
γgesso peso especÌfico do gesso
γmat peso especÌfico do material
γq coeficiente de ponderaÁ„o para aÁıes vari·veis diretas

62. 2006 8-62 ufpr/tc405
γreb peso especÌfico do reboco
γs coeficiente de ponderaÁ„o da resistÍncia do aÁo
γtij peso especÌfico do tijolo
ρ1 taxa de armadura existente na regi„o prÛxima ao apoio
τRd tens„o resistente de c·lculo ao cisalhamento
8.12.2 Símbolos subscritos
bal balanÁo
bar barra
conc arm concreto armado
cont piso contra-piso
cor corrigido
edif com edifÌcio comercial
ef efetivo
fiss fissuraÁ„o
gesso gesso
lim limite
maior maior
mat material
menor menor
min mÌnimo
nec necess·rio
par parede
pos positivo
princ principal
reb reboco
taco taco
tij tijolo
8.13 Exercícios
Ex. 8.1: Dimensionar e detalhar as armaduras positivas e negativas do painel de lajes
abaixo representado.
Dados:
− concreto: C20; e
− aÁo: CA-60.
Considerar:
− somente solicitaÁıes normais (momento fletor);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura da laje (h): 11 cm;
− altura ˙til da laje (d): 8 cm;
− carga permanente (gk): 4,5 kN/m2
(peso prÛprio incluÌdo); e
− carga acidental (qk): 2,0 kN/m2
.
Obs.:
− a carga acidental atua simultaneamente nas duas lajes;
− as armaduras das lajes devem ser alternadas; e
− as dimensıes da figura correspondem a centÌmetros.

63. 2006 8-63 ufpr/tc405
Ex. 8.2: Para o painel abaixo indicado, determinar o valor da carga acidental uniformemente
distribuÌda (qk) que as lajes podem suportar.
Dados:
− concreto: C20; e
− aÁo: CA-50.
Considerar:
− somente solicitaÁıes normais (momento fletor);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura da laje (h): 12 cm;
− altura ˙til da laje (d): 9 cm;
− armadura positiva: 1 φ de 8 mm @ 15 cm nas duas direÁıes;
− armadura negativa: 1 φ de 8 mm @ 10 cm; e
− carga permanente (gk): 5 kN/m2
(peso prÛprio incluÌdo).
Obs.:
− a carga acidental atua simultaneamente nas duas lajes.
Ex. 8.3: Dimensionar e detalhar as armaduras positivas e negativas do painel de lajes
abaixo representado.
Dados:
− concreto: C25; e
− aÁo: CA-60.
7 m 7 m
4 m
15
15
300 4351515 15
660L1 L2

64. 2006 8-64 ufpr/tc405
Considerar:
− somente solicitaÁıes normais (momento fletor);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura da laje (h): 10 cm;
− altura ˙til da laje (d): 7 cm;
− carga permanente (gk): 4 kN/m2
(peso prÛprio incluÌdo); e
− carga acidental (qk): 2 kN/m2
.
Obs.:
− a carga acidental atua simultaneamente nas duas lajes;
− as armaduras das lajes devem ser alternadas; e
− as dimensıes da figura correspondem a centÌmetros.
Ex. 8.4: A figura abaixo representa a forma de um pavimento de um edifÌcio. Sabendo-se
que as lajes ser„o carregadas, alÈm do peso prÛprio, por uma carga de revestimentos de
1,50 kN/m2
e por uma carga acidental igual a 2,0 kN/m2
, pede-se determinar e detalhar as
armaduras positivas e negativas do painel de lajes.
Dados:
− concreto: C25; e
− aÁo: CA-50.
Considerar:
− somente solicitaÁıes normais (momento fletor);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura da laje (h): 10 cm;
− altura ˙til da laje (d): 7 cm; e
− peso especÌfico do concreto armado: 25 kN/m3
.
Obs.:
− a carga acidental atua simultaneamente nas trÍs lajes; e
− as armaduras das lajes devem ser alternadas.
20 20
20 520 20
20
20
300
20
400
300
L2
L1

65. 2006 8-65 ufpr/tc405
4,0 m6,0 m
4,0 m
2,5 mL1
L2 L3
Ex. 8.5: A figura abaixo representa um painel de lajes de um pavimento de um edifÌcio.
Sabendo-se que as lajes est„o carregadas, alÈm do peso prÛprio, por uma carga de
revestimentos de 1,50 kN/m2
e por uma carga acidental igual a 2,0 kN/m2
, pede-se determinar as
armaduras positivas e negativas da laje L3.
Dados:
− concreto: C25; e
− aÁo: CA-60.
Considerar:
− somente solicitaÁıes normais (momento fletor);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura da laje (h): 11 cm;
− altura ˙til da laje (d): 8 cm; e
− peso especÌfico do concreto armado: 25 kN/m3
.
Obs.:
− a carga acidental atua simultaneamente nas trÍs lajes; e
− as armaduras das lajes devem ser alternadas.
L1 L2
L3
4 m
2,4 m
3 m 3 m

66. 2006 8-66 ufpr/tc405
Ex. 8.6: Apresenta-se, na figura abaixo, o esquema estrutural de um pavimento constituÌdo
por trÍs lajes maciÁas de concreto armado. Determinar as armaduras necess·rias nas posiÁıes
N1, N2 e N3 (cm2
/m).
Dados:
− concreto: C25; e
− aÁo: CA-60.
Considerar:
− somente solicitaÁıes normais (momento fletor);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura da laje (h): 10 cm;
− altura ˙til da laje (d): 7 cm;
− carga permanente (gk): 4 kN/m2
(peso prÛprio incluÌdo); e
− carga acidental (qk): 2 kN/m2
.
Obs.:
− a carga acidental atua simultaneamente nas trÍs lajes; e
− as dimensıes da figura correspondem a centÌmetros.
Ex. 8.7: Determinar a m·xima carga acidental (qk) que o painel de laje abaixo representado
pode suportar.
Dados:
− concreto: C25; e
− aÁo: CA-60.
Considerar:
− somente solicitaÁıes normais (momento fletor);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura da laje (h): 11 cm;
− altura ˙til da laje (d): 8 cm;
− armadura positiva: 1 φ de 10 mm @ 15 cm nas duas direÁıes;
− armadura negativa: 1 φ de 10 mm @ 10 cm; e
− carga permanente (gk): 4 kN/m2
(peso prÛprio incluÌdo).
Obs.:
− a carga acidental atua simultaneamente nas duas lajes.
L1
L2
L3
200 400
600
400
400
200 700
200
N1
N2
N3

67. 2006 8-67 ufpr/tc405
Ex. 8.8: Determinar, para o painel de lajes abaixo representado:
a. o diagrama de momentos fletores (valores de c·lculo) na direÁ„o x;
b. a armadura negativa necess·ria na borda (encontro) das lajes L1/L2; e
c. a armadura positiva, na direÁ„o x, da laje L3.
Dados:
− concreto: C25; e
− aÁo: CA-60.
Considerar:
− somente solicitaÁıes normais (momento fletor);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 1 (γg = 1,35, γq = 1,5,
γc = 1,4 e γs = 1,15);
− espessura da laje (h): 12 cm;
− altura ˙til da laje (d): 9 cm;
− revestimento: 1 kN/m2
;
− carga acidental (qk): 6 kN/m2
; e
− peso especÌfico do concreto armado: 25 kN/m3
.
Obs.:
− a carga acidental atua simultaneamente nas trÍs lajes; e
− as armaduras das lajes devem ser alternadas.
2,2 m 5,0 m
5,0 m
L1 L2
L2
4,2 m
9,0 m
6,0 m
L1
L3
3,0 m
6,0 m
7,0 m
x
y

68. 2006 8-68 ufpr/tc405
Ex. 8.9: Determinar o diagrama de momentos fletores de c·lculo sobre os eixos u e v do
painel de lajes abaixo representado.
Considerar:
− somente solicitaÁıes normais (momento fletor);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− carga permanente nas lajes (gk): 4 kN/m2
(peso prÛprio incluÌdo);
− carga acidental nas lajes (qk): 2 kN/m2
; e
− peso da parede (ppar): 4,8 kN/m.
Obs.:
− a carga acidental atua simultaneamente em todas as lajes.
Ex. 8.10: Determinar a m·xima carga acidental (qk) que o painel de lajes abaixo
representado podem suportar.
Dados:
− concreto: C25; e
− aÁo: CA-50.
Considerar:
− somente solicitaÁıes normais (momento fletor);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura da laje (h): 10 cm;
− altura ˙til da laje (d): 7 cm;
− armadura positiva: 1 φ de 6,3 mm @ 12 cm nas duas direÁıes;
− armadura negativa: 1 φ de 8 mm @ 10 cm; e
− carga permanente (gk): 4 kN/m2
(peso prÛprio incluÌdo).
Obs.:
− a carga acidental atua simultaneamente nas duas lajes.
v
u
4m
4 m
3m
1 m
2m 4m4m
4m4m2m
L4
L3
L2L1
3m
1 m
parede vazado

69. 2006 8-69 ufpr/tc405
Ex. 8.11: Determinar o espaÁamento necess·rio para as barras N1 e N2 do painel de laje
abaixo representado.
Dados:
− concreto: C20; e
− aÁo: CA-50.
Considerar:
− somente solicitaÁıes normais (momento fletor);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura da laje (h): 10 cm;
− altura ˙til da laje (d): 7 cm;
− carga permanente (gk): 4 kN/m2
(peso prÛprio incluÌdo);
− carga acidental (qk): 2 kN/m2
;
− armadura positiva (N2): φ de 6,3 mm; e
− armadura negativa (N1): φ de 8 mm.
Obs.:
− a carga acidental atua simultaneamente nas duas lajes.
Ex. 8.12: Para a laje abaixo indicada, determinar:
a. o diagrama de momentos fletores de calculo das lajes L1, L2 e L3, na direÁ„o x;
b. a armadura positiva (cm‚/m) da laje L2, na direÁ„o y; e
c. a armadura negativa (cm‚/m) entre as lajes L2 e L3, na direÁ„o x.
Dados:
− concreto: C25; e
− aÁo: CA-60.
Considerar:
− somente solicitaÁıes normais (momento fletor);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura da laje (h): 10 cm;
− altura ˙til da laje (d): 7 cm;
5,0 m 3,2 m
4,0 m
L1 L2
5,0 m 3,2 m
4,0 m
L1 L2
N1
N2

70. 2006 8-70 ufpr/tc405
− carga permanente (gk): 4 kN/m2
(peso prÛprio incluÌdo); e
− carga acidental (qk): 2 kN/m2
.
Obs.:
− a laje L1 È em balanÁo, apoiada apenas na sua borda direita (ligaÁ„o com a laje L2);
− as demais lajes s„o suportadas por vigas;
− a regi„o entre as lajes L2 e L4 n„o tem laje (vazio);
− a laje L3 tem uma parede com peso de 2,5 kN/m2
e altura 2,8 m (·rea hachureada); e
− as cargas acidentais atuam simultaneamente em todas as lajes.
Ex. 8.13: Determinar as armaduras positivas e negativas (cm2
/m) na direÁ„o x do conjunto
de lajes abaixo representado.
Dados:
− concreto: C25; e
− aÁo: CA-50.
Considerar:
− somente solicitaÁıes normais (momento fletor);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura da laje (h): 12 cm;
− altura ˙til da laje (d): 9 cm;
− carga permanente (gk): 5 kN/m2
(peso prÛprio incluÌdo); e
− carga acidental (qk): 3 kN/m2
.
Obs.:
− a carga acidental atua simultaneamente nas duas lajes;
− as armaduras das lajes devem ser alternadas; e
− apresentar, ao final dos c·lculos, o esquema das armaduras, com as indicaÁıes das
·reas (cm2
/m).
x
y
parede
pilar
vazado
2,0 m2,0 m4,0 m1,5 m
L2L1 L3
L4 3,0 m
4,0 m

71. 2006 8-71 ufpr/tc405
Ex. 8.14: Determinar, para a laje abaixo representada, a altura h mÌnima (m˙ltiplo de 5 cm),
de tal modo que a resistÍncia aos momentos fletores ocorra sem a necessidade de armadura de
compress„o.
Dados:
− concreto: C25; e
− aÁo: CA-60.
Considerar:
− somente solicitaÁıes normais (momento fletor);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 1 (γg = 1,35, γq = 1,5,
γc = 1,4 e γs = 1,15);
− espessura da laje: h = d + 4 cm;
− revestimento: 1 kN/m2
;
− carga acidental (qk): 10 kN/m2
; e
− peso especÌfico do concreto armado: 25 kN/m3
.
12 m
12 m L1
6,0 m 4,0 m
4,0 m
5,0 m
L1
L2
P6
P2
P4 P5
P7
P1 P3
V5AV5Bx
y
V4
V6
V1A V1B
V3
V2

72. 2006 8-72 ufpr/tc405
Ex. 8.15: A planta de formas abaixo indicada representa um conjunto de quatro lajes
maciÁas de concreto armado. Levando-se em consideraÁ„o que na extremidade livre das lajes em
balanÁo L3 e L4 atua uma carga de 2 kN/m na vertical e uma carga horizontal de 0,8 kN/m
posicionada a 80 cm do piso, determinar:
a. as armaduras positivas (cm2
/m) para a laje L1; e
b. as armaduras negativas (cm2
/m) para as lajes L2 e L3.
Dados:
− concreto: C25; e
− aÁo: CA-60.
Considerar:
− somente solicitaÁıes normais (momento fletor);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura da laje (h): 10 cm;
− altura ˙til da laje (d): 7 cm;
− carga permanente (gk): 4 kN/m2
(peso prÛprio incluÌdo); e
− carga acidental (qk): 3 kN/m2
.
Obs.:
− a carga acidental atua simultaneamente nas lajes; e
− as dimensıes da figura correspondem a centÌmetros.
Ex. 8.16: Para o painel de laje abaixo representado, determinar:
a. o esquema de carga atuante na viga V2; e
b. as condiÁıes de seguranÁa quanto ao estado limite ˙ltimo, solicitaÁıes tangenciais.
Sobre todas as vigas do pavimento existe parede de peso equivalente a 2,2 kN/m2
e altura
2,2 m.
Dados:
− concreto: C25; e
− aÁo: CA-60.
Considerar:
− somente solicitaÁıes tangenciais (forÁa cortante);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura da laje (h): 10 cm;
− altura ˙til da laje (d): 7 cm;
355
20
110205355
110
20
20
20
V1A
V3
V2
V1B
P1 V6
V4
L1 L2
P6P5
P3
20
V5
P2
P4
20
L4
L3
580

73. 2006 8-73 ufpr/tc405
− acabamento dos pisos:
! regularizaÁ„o: 0,5 kN/m2
;
! revestimento: 0,7 kN/m2
;
− carga acidental (qk): 3 kN/m2
; e
− peso especÌfico do concreto armado: 25 kN/m3
.
Obs.:
− as dimensıes da figura correspondem a centÌmetros; e
− as vigas devem ser admitas como simplesmente apoiada nos pilares.
Ex. 8.17: Para o painel de laje abaixo representado, determinar:
a. o esquema de cargas (permanente e acidental) atuantes na viga V5; e
b. as condiÁıes de seguranÁa quanto ao estado limite ˙ltimo, solicitaÁıes tangenciais.
Dados:
− concreto: C25; e
− aÁo: CA-60.
Considerar:
− somente solicitaÁıes tangenciais (forÁa cortante);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura das lajes (h):
! L1: 12 cm;
! L2: 8 cm;
− altura ˙til das lajes: d = h ñ 3 cm;
− acabamento dos pisos:
! regularizaÁ„o: 0,5 kN/m2
;
! revestimento: 1,0 kN/m2
;
− carga acidental (qk): 2,0 kN/m2
;
− dimensıes das vigas: 20 cm x 50 cm; e
− peso especÌfico do concreto armado: 25 kN/m3
.
Obs.:
− as vigas devem ser admitas como simplesmente apoiada nos pilares.
V1 ñ 15 x 60
L1
h = 10 cm
L2
h = 10 cm
V2 ñ 15 x 60
V3ñ15x60
V4ñ15x60
V5ñ15x60
285
285 285
P1 P2
P3 P4

74. 2006 8-74 ufpr/tc405
Ex. 8.18: O condomÌnio de um certo edifÌcio pretende aproveitar a laje de cobertura para
construir um depÛsito e decidiu consultar um especialista para opinar sobre a viabilidade da
proposta.
O depÛsito a ser construÌdo ser· em alvenaria de tijolos furados, 15 cm de espessura (tijolos
de 10 cm + reboco de 2,5 cm por face) com 2,8 m de altura. Possuir· laje de cobertura (L2)
impermeabilizada com carga total (valor caracterÌstico) de 3,0 kN/m2
.
Levantando informaÁıes do projeto estrutural a Època da construÁ„o, soube-se que:
− a laje de cobertura existente (L1) foi dimensionada para suportar um momento fletor
solicitante de c·lculo igual a 10 kNm/m na direÁ„o x e 20 kNm/m na direÁ„o y.
− A viga V1 foi dimensionada para suportar um momento fletor solicitante de c·lculo
igual a 120 kNm.
Considerando as informaÁıes fornecidas, vocÍ autorizaria ou n„o a construÁ„o do depÛsito?
Justifique sua resposta.
Dados:
− concreto: C25; e
− aÁo: CA-60.
Considerar:
− somente solicitaÁıes normais (momento fletor);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura da laje L1: 10 cm;
− acabamento do piso da laje L1:
! regularizaÁ„o: 0,5 kN/m2
;
! impermeabilizaÁ„o: 0,5 kN/m2
;
− carga acidental da laje L1: 0,5 kN/m2
;
− dimensıes da viga V1: 20 cm x 50 cm; e
− peso especÌfico do concreto armado: 25 kN/m3
.
Obs.:
− para o levantamento de cargas, desprezar as aberturas de portas e janelas;
− a viga V1 sÛ recebe carga da laje (L1) existente (n„o existe parede sobre ela);
− a viga V1 pode ser considerada como simplesmente apoiada nos pilares; e
− ignorar as verificaÁıes de forÁa cortante nas lajes e vigas.
6,0 m 4,0 m
4,0 m
5,0 m
L1
h = 12 cm
L2
h = 8 cm
P6
P2
P4 P5
P7
P1 P3
V5AV5B
V4
V6
V1A V1B
V3
V2

75. 2006 8-75 ufpr/tc405
Ex. 8.19: No projeto de lajes comuns de edifÌcios de concreto armado (lajes sem armadura
de compress„o), apÛs o prÈ-dimensionamento (fixaÁ„o da altura da laje), deve-se:
a. verificar os esforÁos de cisalhamento;
b. dimensionar a armadura de flex„o; e
c. verificar as deformaÁıes (flechas).
Considerando apenas os itens a e b acima (ignorar as deformaÁıes), determine o m·ximo
valor possÌvel de lx para a laje abaixo representada.
Dados:
− concreto: C20; e
− aÁo: CA-50.
Considerar:
− solicitaÁıes normais (momento fletor) e solicitaÁıes tangenciais (forÁa cortante);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura da laje (h): 12 cm;
− altura ˙til da laje (d): 9,5 cm;
− relaÁ„o entre v„os (ly / lx); 1,5;
− carga permanente (gk): 4 kN/m2
(peso prÛprio incluÌdo); e
− carga acidental (qk): 1,5 kN/m2
.
Obs.:
− adotar para lx um valor m˙ltiplo de 5 cm.
L2
Laje impermeabilizada
com carga total igual a
3,0 kN/m
2
Vista frontal
do depÛsito
3,0 m
3,0 m 2,80 m
¡rea prevista
para o depÛsito
(no meio da laje
de cobertura)
8,0 m
5,0 m
V1
Laje de cobertura
(existente)
h = 10 cm
L1
y
x

76. 2006 8-76 ufpr/tc405
Ex. 8.20: Para a estrutura abaixo representada, determinar:
a. o esquema de carga atuante na viga V7; e
b. as condiÁıes de seguranÁa das lajes quanto ao estado limite ˙ltimo, solicitaÁıes
tangenciais.
Sobre todas as vigas do pavimento existe parede de peso equivalente a 2,2 kN/m2
e altura
2,3 m.
Dados:
− concreto: C25; e
− aÁo: CA-60.
Considerar:
− somente solicitaÁıes tangenciais (forÁa cortante);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura da laje (h): 10 cm;
− altura ˙til da laje (d): 7 cm;
− carga permanente nas lajes (gk): 4 kN/m2
(peso prÛprio incluÌdo);
− carga acidental nas lajes (qk): 2 kN/m2
; e
− peso prÛprio das vigas: 3 kN/m.
Obs.:
− as vigas devem ser admitas como simplesmente apoiada nos pilares.
lx
ly
P6
4,0 m 4,0 m
1,2m4,0m1,2m
3,2m3,2m
P1
P2 P3
P4 P5
V1
V2
V3
V4
V5
V6
V7B
V8
L1
V7CV7A
L2
L3

77. 2006 8-77 ufpr/tc405
Ex. 8.21: Para a estrutura abaixo representada, determinar:
a. o esquema de carga atuante na viga V2; e
b. as condiÁıes de seguranÁa das lajes quanto ao estado limite ˙ltimo, solicitaÁıes
tangenciais.
Sobre todas as vigas do pavimento existe parede de peso equivalente a 2,8 kN/m2
e altura
2,2 m.
Dados:
− concreto: C25; e
− aÁo: CA-60.
Considerar:
− somente solicitaÁıes tangenciais (forÁa cortante);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura da laje (h): 10 cm;
− altura ˙til da laje (d): 7 cm;
− acabamento dos pisos (revestimento + regularizaÁ„o): 1,5 kN/m2
;
− carga acidental (qk): 2 kN/m2
; e
− peso especÌfico do concreto armado: 25 kN/m3
.
Obs.:
− as vigas devem ser admitas como simplesmente apoiada nos pilares.
Ex. 8.22: Para a estrutura abaixo representada, determinar:
a. o m·ximo momento fletor solicitante de c·lculo atuante na viga V4; e
b. as condiÁıes de seguranÁa das lajes quanto ao estado limite ˙ltimo, solicitaÁıes
tangenciais.
Sobre todas as vigas do pavimento existe parede de peso equivalente a 8 kN/m.
V4B
V6B
V3
P1 P2
P3 P4
P5 P6
V1
V2
L1
L3
L2
V4A
V6A
6,0 m
3,0 m
4,0 m
3,0 m 3,0 m
V5

78. 2006 8-78 ufpr/tc405
Dados:
− concreto: C25; e
− aÁo: CA-60.
Considerar:
− somente solicitaÁıes tangenciais (forÁa cortante);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura da laje (h): 10 cm;
− altura ˙til da laje (d): 7 cm;
− acabamento dos pisos (revestimento + regularizaÁ„o): 1,5 kN/m2
;
− carga acidental (qk): 2 kN/m2
; e
− peso especÌfico do concreto armado: 25 kN/m3
.
Obs.:
− as dimensıes da figura correspondem a centÌmetros; e
− as vigas devem ser admitas como simplesmente apoiada nos pilares.
Ex. 8.23: Determinar o carregamento atuante nos pilares da estrutura abaixo representada.
Sobre todas as vigas do pavimento existe parede de peso equivalente a 9 kN/m.
Considerar:
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura da laje (h): 10 cm;
− acabamento dos pisos:
! regularizaÁ„o: 0,5 kN/m2
;
! revestimento: 1,0 kN/m2
;
− carga acidental (qk): 3,0 kN/m2
;
− dimensıes das vigas: 20 cm x 50 cm; e
− peso especÌfico do concreto armado: 25 kN/m3
.
Obs.:
− as dimensıes da figura correspondem a centÌmetros; e
− as vigas devem ser admitas como simplesmente apoiada nos pilares.
V4ñ20X50
P1
20X20
V1 ñ 20X50
V2 ñ 20X50
V3 ñ 20X50
L1
h = 10 cm
L2
h = 10 cm
P4
20X20
P3
20X20
P2
20X20
480
20 20
280
280
20
20
20
V5ñ20X50

79. 2006 8-79 ufpr/tc405
Ex. 8.24: Determinar o carregamento atuante nos pilares da estrutura abaixo representada.
Considerar:
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− carga permanente nas lajes (gk): 4 kN/m2
(peso prÛprio incluÌdo);
− carga acidental nas lajes (qk): 2 kN/m2
; e
− peso prÛprio das vigas: 3 kN/m.
Obs.:
− as vigas devem ser admitas como simplesmente apoiada nos pilares.
80
20
20
20
580
V2
V4
V3
V1
P2
V7
V5
L1
L2
P5
P4
P1
380
20 20
80
20
20
20
V6
P3
P6
580
380
20
3 m
4 m
4 m
3 m 6 m
P1 P2
P3 P4
P5 P6
V6
V7
V1
V2
V3
V4
V5
L1
L2

80. 2006 8-80 ufpr/tc405
Ex. 8.25: Determinar a m·xima carga acidental qk que as lajes L1 e L2 s„o capazes de
suportar, sabendo-se que:
− as armaduras positivas (N1, N2, N3 e N4) s„o constituÌdas por barras de 5 mm
espaÁadas a cada 10 cm;
− a armadura negativa (N5) È constituÌda por barras de 8 mm espaÁadas a cada 10 cm;
e
− o carregamento m·ximo que a viga V4 È capaz de suportar, decorrente das reaÁıes
das lajes e de seu peso prÛprio, È igual a 25 kN/m (valor caracterÌstico).
Dados:
− concreto: C20; e
− aÁo: CA-50.
Considerar:
− somente solicitaÁıes normais (momento fletor);
− estado limite ˙ltimo, combinaÁıes normais, edificaÁ„o tipo 2 (γg = 1,4, γq = 1,4, γc = 1,4
e γs = 1,15);
− espessura da laje (h): 10 cm;
− altura ˙til da laje (d): 7 cm;
− carga permanente (gk): 4 kN/m2
(peso prÛprio incluÌdo);
− peso prÛprio das vigas: 1,5 kN/m.
Obs.:
− a carga acidental atua simultaneamente nas duas lajes.
V2
N2
N4
N1
N3
L1 L2
480 cm
N5
V1
V3
V4
V5
400 cm 400 cm
480 cm