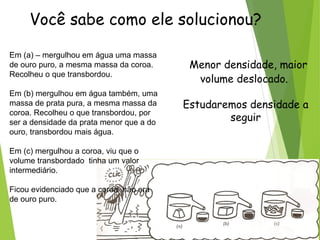
(1) Arquimedes descobriu como determinar se a coroa do rei Hierão era de ouro puro ou misturada com prata; (2) Ele percebeu que o volume de água deslocado por um objeto depende de sua densidade; (3) Arquimedes mergulhou a coroa, ouro puro e prata pura em água e comparou os volumes deslocados para provar que a coroa continha prata.

1. C. E. Antonio Dias Lima
Frade – RJ
Aula de Física – Professor Sergio
Hidrostática

2. H i d r o s t á t i c a

3. O Problema de Arquimedes
Conta a lenda que Hierão, rei de Siracusa, encarregou Arquimedes em descobrir se
sua coroa, encomendada a um ourives, foi feita com todo o ouro fornecido, ou se fora
misturada com prata, isso sem danificar sua coroa.
Tomando banho, em um banheiro público, Arquimedes, percebeu que toda a água
derramada era igual ao volume do seu corpo.
Saiu gritando nú pelas ruas: eureka, eureka (achei, achei).

4. Você sabe como ele solucionou?
Em (a) – mergulhou em água uma massa
de ouro puro, a mesma massa da coroa.
Recolheu o que transbordou.
Em (b) mergulhou em água também, uma
massa de prata pura, a mesma massa da
coroa. Recolheu o que transbordou, por
ser a densidade da prata menor que a do
ouro, transbordou mais água.
Em (c) mergulhou a coroa, viu que o
volume transbordado tinha um valor
intermediário.
Ficou evidenciado que a coroa não era
de ouro puro.
Menor densidade, maior
volume deslocado.
Estudaremos densidade a
seguir

5. Densidade / massa específica
CORPOV
m
d =
.SUBSTV
m
=µ
DensidadeDensidade de um Corpo →dde um Corpo →d
m massa do corpo (kg, g,...)→
VC Volume do corpo (m³, cm³, L, ...)→
MassaMassa Específica de uma Substância →Específica de uma Substância →μμ
m massa da substância (kg, g,...)→
VS Volume de substância (m³, cm³, L)→

6. DENSIDADE OU MASSA ESPECÍFICA ?DENSIDADE OU MASSA ESPECÍFICA ?
Melhor exemplo seria um objeto OCO.
DENSIDADE leva em consideração o volume completo do corpo.
MASSA ESPECÍFICA apenas a parte que contêm substância.

7. E x e m p l o
Um corpo possui massa de 2.000 g.
Determine, sua densidade e a massa específica do material
que o constitui.
400 cm3 100 cm3
CORPOV
m
d =
500
000.2
=d
3
/4 cmgd =
SUBSTV
m
=µ
400
000.2
=µ
3
/5 cmg=µ

8. P r e s s ã o
Supondo que sobre
Uma superfície plana de
área A, atuem forças
perpendiculares (Fig.1) .
Cuja resultante é (Fig.2).
Fig. 1 Fig. 2
Definimos :
a pressão média ( Pm )
sobre a superfície por:

9. Unidades no S.I.
No Sistema Internacional, a unidade de
pressão é o pascal (Pa):
1 Pa = 1 pascal = 1 N / m2

10. E x e m p l o
Sobre uma mesa está apoiado um bloco de massa m = 3,5 kg,
na forma de um cubo de aresta 0,20 m, sendo g = 10 m/s².
Calcule a pressão exercida pelo bloco sobre a mesa.
p = F p = 35 = 875 N/m²
A 0,04
F = P = m.g = 3,5.10 = 35N 8,75.10²N/m²
ou
A = 0,20² = 0,04 m² 8,75.10²pa

11. P r i n c í p i o d e S t è v i n
“A diferença de pressões entre dois pontos de
um líquido em equilíbrio hidrostático é
proporcional à diferença de profundidades”
Simon Stevin
(1548 – 1620)

12. 2
1
h2
h1
Δh
p1 = patm + μgh1
p2 = patm + μgh2
Δp = μgΔh

13. Paradoxo Hidrostático
Δh = 0 Δp = 0
p1 = p2 = p3=p4
1 2 3 4
Patm. Patm Patm Patm

14. Pressão Atmosférica
Experimento de Torricelli
O físico e matemático italiano Evangelista
Torricelli construiu o primeiro barômetro.
Um aparelho que mede a pressão
atmosférica.
Evangelista
Torricelli
(1608- 1647)

15. A experiência de Torricelli
Torricelli tomou um tubo de vidro, com cerca de
1 metro de comprimento.
Enchendo-o completamente com mercúrio (fig a)
Tampando a extremidade livre e invertendo o
tubo.
Mergulhou esta extremidade em um recipiente
contendo também mercúrio.
Ao destampar o tubo ele verificou que a coluna
líquida descia até uma altura de 76 cm acima do
mercúrio no recipiente (fig.b).
Conclusão: 1atm = 76 cm de Hg= 760mm Hg

16. Princípio de Pascal
O acréscimo (ou diminuição) de pressão,
produzido em um ponto de um líquido em
equilíbrio, se transmite integralmente
para todos os pontos do líquido.
Blaise Pascal
(1623- 1662)

17. Aplicação

18. Princípio de Arquimedes
O que é Empuxo?
Força vertical dirigida para cima, exercida pelo líquido sobre o corpo
mergulhado.
O valor do empuxo que atua em um corpo mergulhado em um líquido é igual ao
peso do líquido deslocado pelo corpo.
1ª ) Sentido oposto ao peso do corpo ;
2ª ) Intensidade dada por E = dL.Vd.g
dL densidade do líquido.
Vd volume do líquido deslocado.
g aceleração da gravidade. Arquimedes
(298 a.C. - 212 a.C.)

19. Fluido deslocado
Por fluido deslocado, entendemos o fluido que preenche o
volume ocupado pelo corpo, abaixo da superfície livre do fluido.
dc >df - Pc > E – o corpo afunda
dc =df - Pc = E – o corpo fica em equilíbrio
dc < df - E > Pc – o corpo sobe até ficarem equilíbrio,
Parcialmente submerso conforme figura A
dc=densidade do corpo Pc=peso do corpo
df=densidade do fluido E=Empuxo