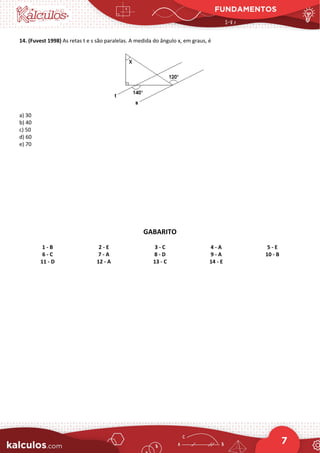
Este documento contém 14 exercícios de geometria plana e trigonometria, com figuras geométricas e informações angulares e de distâncias. Os exercícios envolvem conceitos como retas paralelas, triângulos isósceles, ângulos internos e externos, e relações trigonométricas envolvendo distância, altitude e ângulo de elevação. Há também um gabarito no final com as respostas corretas.

1. LISTAS DE EXERCÍCIOS
FUNDAMENTOS

2. FUNDAMENTOS
1
01. (Famerp 2019) A figura, feita em escala, indica um painel formado por sete retângulos amarelos idênticos e dois
retângulos azuis idênticos. Cada retângulo azul tem dimensões x e y, ambas em metros.
Na situação descrita, x y
− é igual a
a) 2,5 m.
b) 4 m.
c) 3,5 m.
d) 3 m.
e) 2 m.
02. (Espm 2019) A figura abaixo representa uma parte de um bairro, onde os segmentos são as ruas e os pontos são
as esquinas. Como só podemos caminhar pelas ruas, a distância entre os pontos A e B é de 6 quarteirões.
O número de esquinas assinaladas no mapa, que são equidistantes de A e B, é igual a
a) 5
b) 6
c) 9
d) 8
e) 7

3. FUNDAMENTOS
2
03. (Unicamp 2019) No triângulo ABC exibido na figura a seguir, AD é a bissetriz do ângulo interno em A, e AD DB.
=
O ângulo interno em A é igual a
a) 60 .
°
b) 70 .
°
c) 80 .
°
d) 90 .
°
04. (Mackenzie 2018) O triângulo PMN é isósceles de base MN.
Se p, m e n são os ângulos internos do triângulo, como representados na figura, então podemos afirmar que suas
medidas valem, respectivamente,
a) 50 , 65 , 65
° ° °
b) 65 , 65 , 50
° ° °
c) 65 , 50 , 65
° ° °
d) 50 , 50 , 80
° ° °
e) 80 , 80 , 40
° ° °

4. FUNDAMENTOS
3
05. (Fatec 2017) Em um círculo recortado em papel cartão foi feito o desenho de um homem estilizado. Esse círculo
foi utilizado para montar uma roleta, conforme a figura 1, fixada em uma parede. Quando a roleta é acionada, o círculo
gira livremente em torno do seu centro, e o triângulo indicador permanece fixo na parede.
Considerando, inicialmente, a imagem do homem na posição da figura 1, obtém-se, após a roleta realizar uma rotação
de três quartos de volta, no sentido horário, a figura representada em
a) b) c) d) e)
06. (Ifsp 2016) As medidas dos ângulos de um triângulo são, respectivamente, x, 8x e 9x. Diante do exposto, assinale
a alternativa que apresenta o valor de x.
a) 7.
b) 8,5.
c) 10.
d) 11,8.
e) 12.
07. (Espm 2016) Num mapa, uma estrada retilínea passa sucessivamente pelas cidades A, B e C e uma cidade D,
distante 120 km de A, está localizada de tal forma que o ângulo 
DAB mede 36 .
° Um viajante fez o trajeto AB, BD e
DC, percorrendo em cada trecho a mesma distância. Se ele tivesse ido diretamente de A até C, teria percorrido uma
distância de
a) 120 km
b) 60 3 km
c) (120 cos 36 ) km
⋅ °
d)
120
km
cos 36°
e) 140 km

5. FUNDAMENTOS
4
08. (Fatec 2015) Ao se recortar a figura 1, obteve-se a figura 2.
Assinale a alternativa que apresenta o complemento correto da figura 2 para se refazer a figura 1.
a)
b)
c)
d)
e)

6. FUNDAMENTOS
5
09. (Fgv 2015) A figura representa um triângulo ABC, com E e D sendo pontos sobre AC. Sabe-se ainda que
AB AD,
= CB CE
= e que ˆ
EBD mede 39 .
°
Nas condições dadas, a medida de 
ABC é
a) 102°
b) 108°
c) 111°
d) 115°
e) 117°
10. (Espm 2014) Um avião voava a uma altitude e velocidade constantes. Num certo instante, quando estava a 8 km
de distância de um ponto P, no solo, ele podia ser visto sob um ângulo de elevação de 60° e, dois minutos mais tarde,
esse ângulo passou a valer 30°, conforme mostra a figura abaixo.
A velocidade desse avião era de
a) 180 km/h
b) 240 km/h
c) 120 km/h
d) 150 km/h
e) 200 km/h
11. (Mackenzie 2014) Na figura abaixo, a e b são retas paralelas.
A afirmação correta a respeito do número que expressa, em graus, a medida do ângulo é
a) um número primo maior que 23.
b) um número ímpar.
c) um múltiplo de 4.
d) um divisor de 60.
e) um múltiplo comum entre 5 e 7.
α

7. FUNDAMENTOS
6
12. (Unesp 2013) Um aluno precisa localizar o centro de uma moeda circular e, para tanto, dispõe apenas de um lápis,
de uma folha de papel, de uma régua não graduada, de um compasso e da moeda.
Nessas condições, o número mínimo de pontos distintos necessários de serem marcados na circunferência descrita
pela moeda para localizar seu centro é
a) 3
b) 2
c) 4
d) 1
e) 5
13. (Fgv 2007) Num triângulo isósceles ABC, de vértice A, a medida do ângulo obtuso formado pelas bissetrizes dos
ângulos B e C é 140 .
°
Então, as medidas dos ângulos A,B e C são, respectivamente
a) 120 , 30
° ° e 30°
b) 80 , 50
° ° e 50°
c) 100 , 40
° ° e 40°
d) 90 , 45
° ° e 45°
e) 140 , 20
° ° e 20°

8. FUNDAMENTOS
7
14. (Fuvest 1998) As retas t e s são paralelas. A medida do ângulo x, em graus, é
a) 30
b) 40
c) 50
d) 60
e) 70
GABARITO
1 - B 2 - E 3 - C 4 - A 5 - E
6 - C 7 - A 8 - D 9 - A 10 - B
11 - D 12 - A 13 - C 14 - E