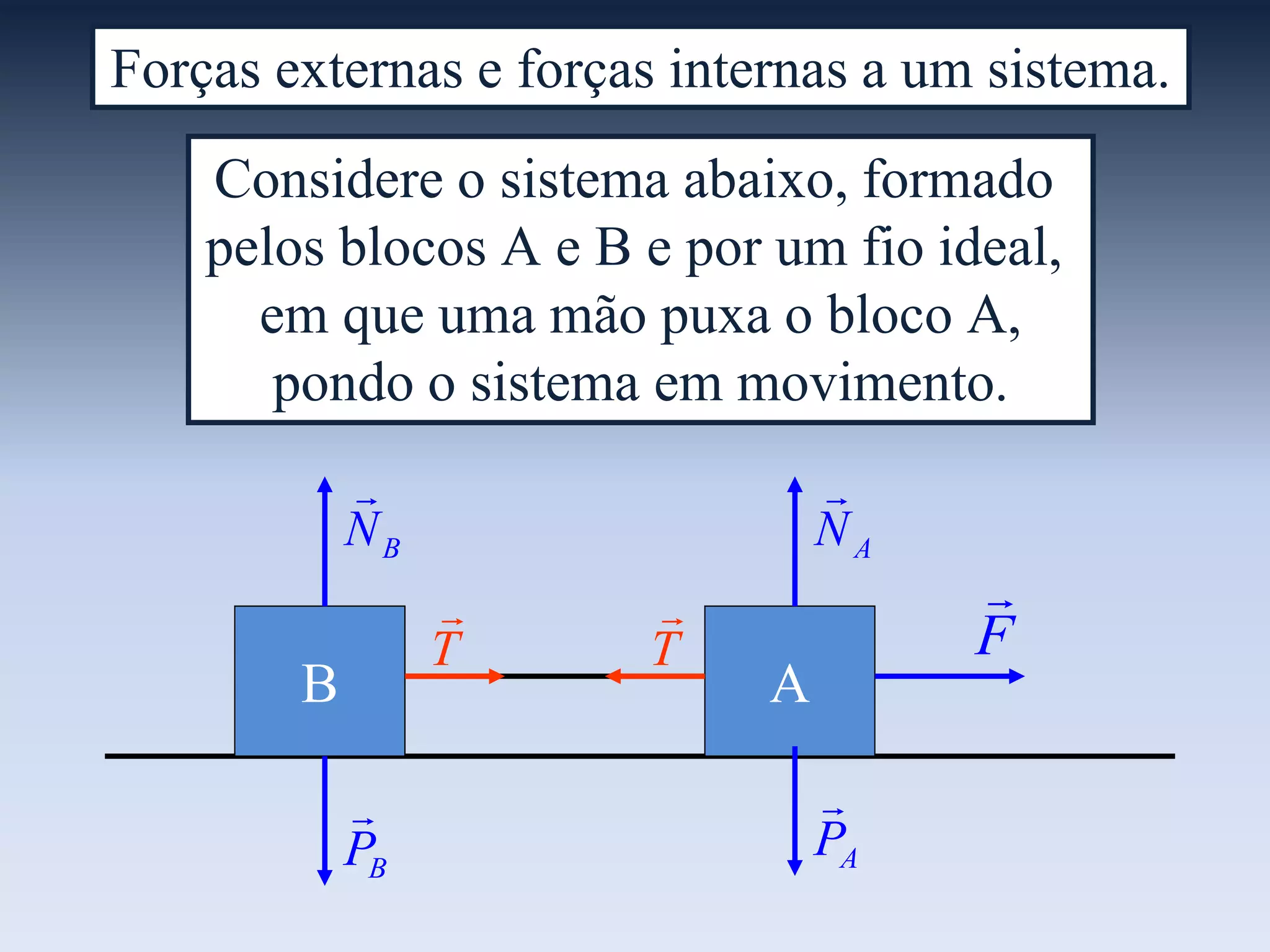
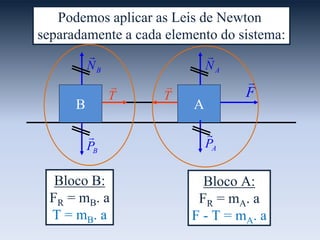
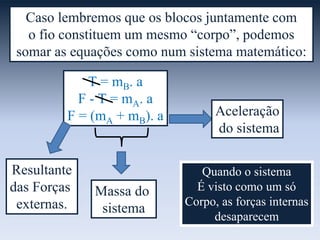
O documento descreve um sistema formado por dois blocos A e B ligados por um fio, onde uma força externa F é aplicada pelo bloco A. Ele explica que forças externas são aplicadas por elementos fora do sistema, como F, enquanto forças internas são aplicadas entre elementos dentro do sistema, como a tração entre os blocos. Também aplica as leis de Newton separadamente aos blocos e ao sistema como um todo, onde as forças internas se anulam.

1. Forças externas e forças internas a um sistema.
Considere o sistema abaixo, formado
pelos blocos A e B e por um fio ideal,
em que uma mão puxa o bloco A,
pondo o sistema em movimento.

NB

NA

T
B

PB

T
A

PA

F

2. Forças externas são exercidas por elementos de fora
do sistema sobre os elementos internos. No exemplo citado,
Temos NA e NB (exercidas pelo solo sobre os blocos),
PA e PB (exercidas pelo planeta sobre os blocos) e F, que é
exercida pela mão (agente externo) ao sistema.
Forças internas são exercidas por elementos do
sistema uns sobre os outros. No exemplo, temos
As forças de tração que A e B trocam entre si,
Por intermédio do fio.

3. Podemos aplicar as Leis de Newton
separadamente a cada elemento do sistema:

NB

NA

T
B

PB
Bloco B:
FR = mB. a
T = mB. a

T
A

F

PA
Bloco A:
FR = mA. a
F - T = mA . a

4. Caso lembremos que os blocos juntamente com
o fio constituem um mesmo “corpo”, podemos
somar as equações como num sistema matemático:
T = mB. a
F - T = mA . a
F = (mA + mB). a
Resultante
das Forças
externas.
Massa do
sistema
Aceleração
do sistema
Quando o sistema
É visto como um só
Corpo, as forças internas
desaparecem