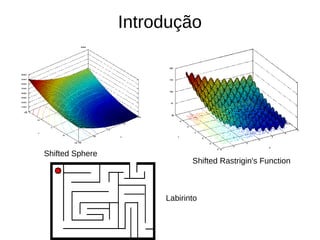
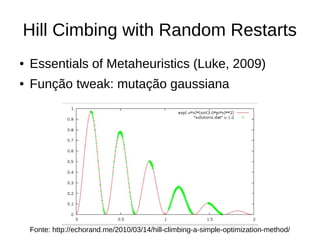
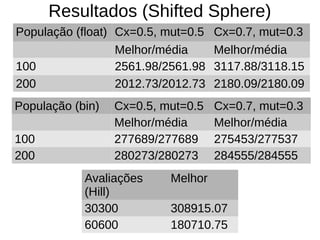
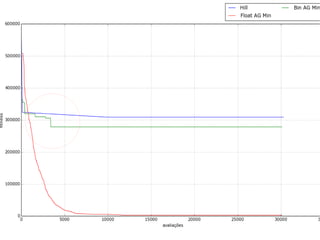
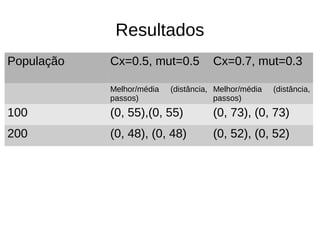
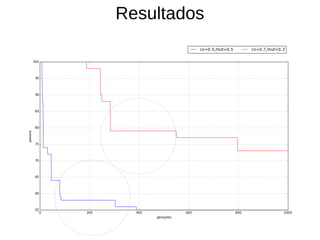
O documento descreve experimentos com algoritmos evolutivos para resolver problemas de otimização contínua e discreta, como a função esfera deslocada e um labirinto. É apresentada a biblioteca DEAP e diferentes representações, operadores genéticos e métodos de seleção. Os resultados mostram que representações binárias com mutação e crossover não geram variedade suficiente, enquanto Hill Climbing é lento para convergir.

1. Exercício 2
Aplicação De Algoritmos Evolutivos
Romualdo André da Costa
@romualdoandre

2. Introdução
Shifted Sphere
Shifted Rastrigin's Function
Labirinto

3. DEAP

4. Representação Real
● População aleatória com distribuição uniforme
● Crossover BLX-α (Eshelman e Shaffer, 1993)
– c = p 1 + β ( p 2 − p 1 )
– Β U (- α ,1+ α )∈
● Mutação Gaussiana
● Seleção (μ+λ)
● Torneio

5. Representação binária
● Biblioteca bitstring
● 32 bits
● Crossover em dois pontos
● Mutação flip bit
● Seleção (μ+λ)
● Torneio

6. Hill Cimbing with Random Restarts
● Essentials of Metaheuristics (Luke, 2009)
● Função tweak: mutação gaussiana
Fonte: http://echorand.me/2010/03/14/hill-climbing-a-simple-optimization-method/

7. Resultados (Shifted Sphere)
População (float) Cx=0.5, mut=0.5 Cx=0.7, mut=0.3
Melhor/média Melhor/média
100 2561.98/2561.98 3117.88/3118.15
200 2012.73/2012.73 2180.09/2180.09
População (bin) Cx=0.5, mut=0.5 Cx=0.7, mut=0.3
Melhor/média Melhor/média
100 277689/277689 275453/277537
200 280273/280273 284555/284555
Avaliações
(Hill)
Melhor
30300 308915.07
60600 180710.75

9. Discussão
● Representação
● Mutação e crossover binários não conseguem
variedade o suficiente.
● Tweak não explora o espaço de busca.
● Hill Climbing: menos memória, mais lento para
convergir.
● Preso em mínimos locais.

10. Labirinto
● d, e, c e b
● Mutação swap
● Crossover de dois pontos
● Máximo de 100 passos
● Multi objetivo: passos e distância
● Paredes
● Torneio

11. Resultados
População Cx=0.5, mut=0.5 Cx=0.7, mut=0.3
Melhor/média (distância,
passos)
Melhor/média (distância,
passos)
100 (0, 55),(0, 55) (0, 73), (0, 73)
200 (0, 48), (0, 48) (0, 52), (0, 52)

12. Resultados

13. Discussão
● + população && + mutação = + diversidade
● Mínimos locais
● Animação!