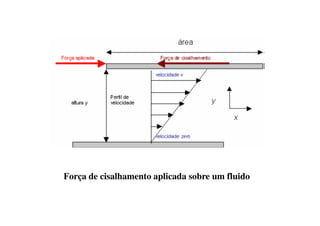
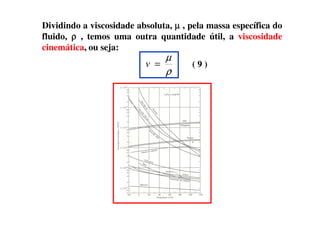
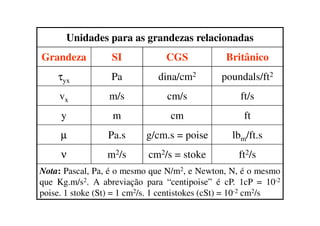
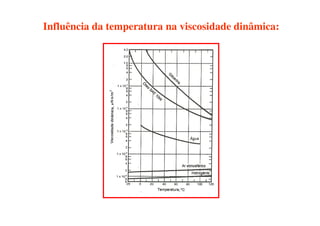
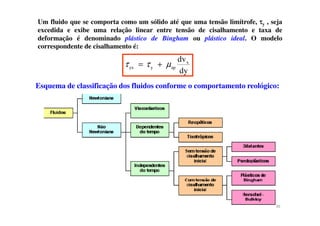
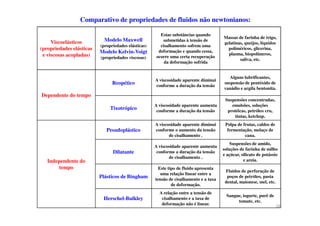
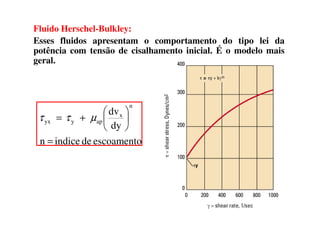
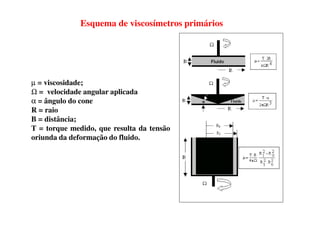
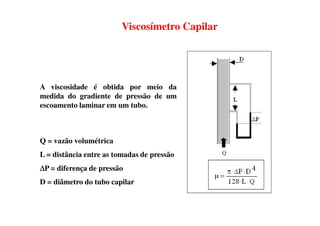
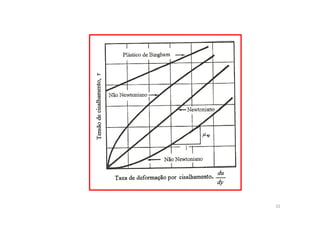
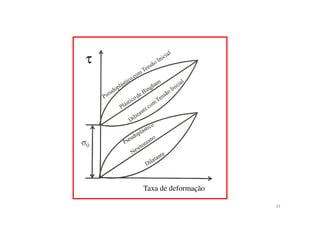
1) O documento discute os fenômenos de transporte, que envolvem a transferência de momento, energia e massa. 2) A mecânica dos fluidos é apresentada, incluindo definições de fluido, velocidade, tensão de cisalhamento e viscosidade. 3) Os principais tópicos incluem introdução à mecânica dos fluidos, equações básicas, métodos de análise e conceitos fundamentais como campo de velocidade e comportamento de fluidos newtonianos.

1. Fenômenos de Transporte I
Aula 01Aula 01
Prof. Dr. Gilberto Garcia Cortez

2. Bibliografia utilizada

3. FENÔMENOS DE TRANSPORTE
A expressão fenômenos de transporte (mais
raramente, fenômenos de transferência) refere-se ao
estudo sistemático e unificado da transferência
de momento (mecânica dos fluidos), energia (transferência
de calor) e matéria (transferência de massa).
O transporte (transferência) destas grandezas e aO transporte (transferência) destas grandezas e a
construção de seus modelos guardam fortes analogias,
tanto físicas como matemáticas, de tal forma que a análise
matemática empregada é praticamente a mesma.

4. 1- Introdução
Mecânica dos fluidos é a ciência que tem por objetivo o estudo do
comportamento físico dos fluidos em movimento e em repouso e das leis
que regem este comportamento.
A mecânica dos fluidos pode ser subdividida no estudo da estática dos
fluidos, onde o fluido está em repouso, e na dinâmica dos fluidos, onde o
fluido está em movimento.
Aplicações da mecânica dos fluidos:
- Ação de fluidos sobre superfícies submersas. Ex.: barragens- Ação de fluidos sobre superfícies submersas. Ex.: barragens
- Equilíbrio de corpos flutuantes. Ex.: embarcações
- Estudo de lubrificações.
- Transporte de sólidos por via pneumática ou hidráulica. Ex.: elevadores
- Cálculo de instalações hidráulicas. Ex.: bombas e turbinas
- Instalações de vapor. Ex.: caldeiras
- Ação de fluidos sobre veículos, aeronaves e edificações (aerodinâmica).

5. 1.1- Definição de fluido
- Fluido é uma substância que não tem forma própria, e que,
se estiver em repouso, não resiste a tensões de cisalhamento.
- Fluido é uma substância que quando submetido a tensões de
cisalhamento (tangenciais), por pequenas que sejam, deforma-
se continuamente.
- Fluidos tendem a escoar (ou fluir) e os sólidos tendem a se
deformar ou dobrar quando interagimos com eles.deformar ou dobrar quando interagimos com eles.
- Assim, os fluidos compreendem as fases líquidas e gasosas
(ou de vapor) das formas físicas nas quais a matéria existe.
- A distinção entre um fluido e o estado sólido da matéria é
clara quando você compara seus comportamentos. Um sólido
deforma-se quando uma tensão de cisalhamento lhe é
aplicada, mas sua deformação não aumenta continuamente
com o tempo.

6. 1.2- Equações básicas
A análise de qualquer problema de mecânica dos fluidos começa,
necessariamente, de modo direto ou indireto, com declarações das
leis básicas que modelam o movimento do fluido. As leis básicas,
aplicáveis a qualquer fluido são:
1- A equação da conservação da massa
2- A segunda lei do movimento de Newton
3- O princípio da quantidade angular3- O princípio da quantidade angular
4- A primeira lei da termodinâmica
5- A segunda lei da termodinâmica
Obviamente, nem todas as leis básicas são necessárias para resolver
um problema. Por outro lado, em muitos deles é necessário buscar
relações adicionais para a análise, na forma de equações de estado
ou outras de caráter constitutivo, que descrevam o comportamento
das propriedades físicas dos fluidos sob determinadas condições.

7. 1.3- Métodos de análise
O primeiro passo na resolução de um problema é definir o sistema
que você está tentando analisar.
Na mecânica dos fluidos, utilizaremos um sistema ou um volume
de controle para resolver um problema.
1.3.1- Sistema
Um sistema é definido como uma quantidade de massa fixa eUm sistema é definido como uma quantidade de massa fixa e
identificável; o sistema é separado do ambiente pelas fronteiras.
As fronteiras podem ser fixas ou móveis; contudo, nenhuma
massa cruza essas fronteiras.

8. 1.3.2- Volume de controle
Um volume de controle é um volume arbitrário no espaço através
do qual o fluido escoa. A fronteira geométrica do volume de
controle é denominado superfície de controle. É sempre importante
tomar cuidado na seleção de um volume de controle, pois a escolha
tem um grande efeito sobre a formulação matemática das leis
básicas.

9. 1.4- Dimensões e unidades
Referimo-nos as quantidades físicas tais como comprimento (L),
tempo (t), massa (M) e temperatura (T) como dimensões.
Unidades são os nomes (e magnitudes) arbitrárias dados às
dimensões primárias adotadas como padrões de medidas.
Ex. A dimensão primária de comprimento pode ser medida em
unidades de metros (m), centímetro (cm), pés (ft), jardas ou milhas.
Cada unidade de comprimento é relacionada às outras por fatoresCada unidade de comprimento é relacionada às outras por fatores
de conversão de unidades.
Ex. 1 milha = 5280 pés = 1609 metros

10. SISTEMAS DE UNIDADES
Sistema Internacional de Unidades (SI)
Massa é o quilograma (Kg)
Comprimento é o metro (m)
Tempo é o segundo (s)
Temperatura é o Kelvin (K)
Força é o Newton (N)
1 N ≡≡≡≡ 1 Kg.m/s2 (secundária)
Sistema de Unidades Métrico Absoluto (CGS)
Massa é o grama (g)
Comprimento é o centímetro (cm)
Tempo é o segundo (s)
Temperatura é o Kelvin (K)
Força é a dina (dina)
1 dina ≡≡≡≡ 1 g.cm/s2 (secundária)

11. Sistema de Unidades Gravitacional Britânico
Massa é o slug (slug)
Comprimento é o pé (ft)
Tempo é o segundo (s)
Temperatura é o Rankine (°°°°R)
Força é a libra-força (lbf)
1 lbf ≡≡≡≡ 1 slug.ft/s2 (secundária)
Sistema de Unidades Inglês Técnico ou de EngenhariaSistema de Unidades Inglês Técnico ou de Engenharia
Massa é a libra-massa (lbm)
Comprimento é o pé (ft)
Tempo é o segundo (s)
Temperatura é o Rankine (°°°°R)
Força é a libra-força (lbf)
1 slug ≡≡≡≡ 32,2 lbm

12. 2c
c
2
lbf.s
ft.lbm
32,2g
g
ft/s32,2xlbm1
lbf1 =≡
A constante de proporcionalidade, gc , tem dimensões e unidades no
sistema inglês técnico.
g
am.
F
c
=
No SI, a constante de proporcionalidade, gc , é sem dimensões e
unitário. Em consequência, a segunda lei de Newton é escrita:unitário. Em consequência, a segunda lei de Newton é escrita:
Nesses sistemas, resulta que a força gravitacional (o peso) sobre um
objeto de massa m é dado por:
am.F =
gm.W =

13. 2. Conceitos fundamentais
2.1- O fluido como um contínuo
Todos os fluidos são compostos de moléculas em constante
movimento.
Um fluido é uma substância infinitamente divisível, um
continuum, e deixamos de lado o comportamento das
moléculas individuais.moléculas individuais.
2.2- Campo de velocidade
Ao lidarmos com fluidos em movimento, estaremos
naturalmente interessados na descrição de um campo de
velocidade.

14. A velocidade em qualquer ponto do campo de escoamento
pode variar de um instante a outro. A representação completa
da velocidade (o campo de velocidade) é dada por:
O vetor velocidade, pode também ser escrito em termos dos
seus três componentes escalares. Denotando os componente
nas direções x, y, z por µµµµ, νννν, ωωωω, escreve-se:
( Escoamento transiente )0
t
V
out)z,y,(x,VV ≠
∂
∂
=
r
rr
nas direções x, y, z por µµµµ, νννν, ωωωω, escreve-se:
Se as propriedades em cada ponto de um campo de
escoamento não mudam com o tempo, o escoamento é
denominado permanente:
kωjνiµV ++=
r
( Escoamento permanente )0
t
V
ouz)y,(x,VV =
∂
∂
=
r
rr
ÔmegaωNi;νMi;µ ===

15. Escoamento Uni, Bi e Tridimensionais
Um escoamento é classificado como uni, bi ou tridimensional de
acordo com o número de coordenadas espaciais necessárias para
especificar seu campo de velocidade.
t)z,y,(x,VV
rr
= ( Escoamento tridimensional e transiente )
z)y,(x,VV
rr
= ( Escoamento tridimensional e permanente )

16. Num escoamento uniforme, a velocidade é constante através de qualquer seção
normal ao escoamento.

17. 2.3- Tensão de cisalhamento e viscosidade
Para um sólido, as tensões são desenvolvidas quando um material é
deformado ou cisalhado elasticamente; para um fluido, as tensões
de cisalhamento aparecem devido ao escoamento viscoso.
Seja uma força F aplicada sobre uma superfície de área A. Essa
força pode ser decomposta segundo a direção normal à superfície e
da tangente, dando origem a uma componente normal e outra
tangencial.tangencial.
tF
nF F

18. Defini-se tensão de cisalhamento como sendo o quociente
entre o módulo da componente tangencial e da área a qual
está aplicada.
Defini-se pressão (tensão normal) como sendo o quociente
A
Ft
=τ
Defini-se pressão (tensão normal) como sendo o quociente
entre o módulo da componente da força normal (força de
compressão) e da área a qual está aplicada.
A
F
P
n
=

19. Considere-se o comportamento de um elemento de fluido entre duas placas
infinitas ilustradas a seguir:
A placa superior movimenta-se a velocidade constante, δδδδu, sob a
influência de uma força aplicada constante, δδδδFx.

20. Força de cisalhamento aplicada sobre um fluido

21. Como aparecem as forças internas? O fluido junto à placa superior irá
se deslocar com velocidade v, enquanto aquele junto à placa inferior
estará com velocidade nula. Em cada seção normal às placas, irá se
formar um diagrama de velocidades, onde cada camada do fluido desliza
sobre a adjacente com uma certa velocidade relativa. Tal deslizamento
entre as camadas origina tensões de cisalhamento. A Figura a seguir
mostra o aparecimento da tensão de cisalhamento, ττττ , devido à
velocidade relativa v1 – v2, que cria um escorregamento entre as duas
camadas indicadas.

22. A tensão de cisalhamento, ττττyx , aplicada ao elemento de fluido é
dado por:
dA
dF
δA
δF
limτ
y
x
y
x
0δ
yx
Ay
==
→ ( 1 )
onde δδδδA é a área do elemento de fluido em contato com aonde δδδδAy é a área do elemento de fluido em contato com a
placa. No incremento de tempo, δδδδt , o elemento de fluido é
deformado da posição MNOP para a posição M’NOP’.
A taxa de deformação do fluido é dada por:
dt
dα
δt
δα
limdeformaçãodetaxa
0δt
==
→
( 2 )

23. O fluido é newtoniano se ττττyx for diretamente proporcional a taxa
de deformação (Equação 2).
A distância δδδδℓ entre os pontos M e M’ é dado por:
( 3 )δtδvδ
δt
δ
δv xx =⇒= l
l
dt
dα
aalproporcionediretamentτyx
δt
xx
ou alternativamente, para pequenos ângulos,
δyδαδ =l ( 4 )
Igualando (3) com (4), temos:
δyδαδtδvx =
δt
δα
δy
δvx
= ( 5 )

24. Aplicando o limite em ambos os lados da igualdade, obtêm-se:
δt
δα
lim
δy
δv
lim
0δt
x
0δy →→
=
dt
dα
dy
dvx
= ( 6 )
dtdy
Assim, se o fluido da figura é newtoniano, temos que:
dy
dv
aalproporcionediretamentéτ x
yx ( 7 )
A tensão de cisalhamento age num plano normal ao eixo dos y

25. A constante de proporcionalidade da equação (7) é a
viscosidade absoluta (ou dinâmica), µµµµ.
Assim, em termos das coordenadas da figura anterior, a lei da
viscosidade de Newton é dada por:
dy
dv
τ x
yx µ= ( 8 )
Fluidos Newtonianos

26. Dividindo a viscosidade absoluta, µµµµ , pela massa específica do
fluido, ρρρρ , temos uma outra quantidade útil, a viscosidade
cinemática, ou seja:
ρ
µ
=ν ( 9 )

27. Unidades para as grandezas relacionadas
Grandeza SI CGS Britânico
τyx Pa dina/cm2 poundals/ft2
vx m/s cm/s ft/s
y m cm fty m cm ft
µ Pa.s g/cm.s = poise lbm/ft.s
ν m2/s cm2/s = stoke ft2/s
Nota: Pascal, Pa, é o mesmo que N/m2, e Newton, N, é o mesmo
que Kg.m/s2. A abreviação para “centipoise” é cP. 1cP = 10-2
poise. 1 stoke (St) = 1 cm2/s. 1 centistokes (cSt) = 10-2 cm2/s

28. Viscosidade de um fluido:
É a propriedade pela qual um fluido oferece resistência ao corte;
É a medida da resistência do fluido à fluência quando sobre ele atua
uma força exterior como por exemplo um diferencial de pressão ou
gravidade;
A viscosidade mede a resistência de um líquido em fluir (escoar) eA viscosidade mede a resistência de um líquido em fluir (escoar) e
não está diretamente relacionada com a densidade do líquido, que é
a relação massa/volume. Por exemplo, o óleo de soja utilizado para
cozinhar é mais viscoso do que a água, embora seja menos denso.
A maioria dos líquidos viscosos fluem facilmente quando as suas
temperaturas aumentam; o comportamento de um fluido quando
varia a temperatura, pressão ou tensão depende do tipo de fluido.

29. Influência da temperatura na viscosidade dinâmica:

30. A viscosidade pode mudar com o tempo (todas as outras
condições ficam constantes);
A coesão molecular é a causa dominante da viscosidade nos
líquidos; à medida que a temperatura de um líquido aumenta,
estas forças coesivas diminuem, resultando uma diminuição da
viscosidade;
Nos gases, a causa dominante são as colisões aleatórias entre as
moléculas do gás; esta agitação molecular aumenta com amoléculas do gás; esta agitação molecular aumenta com a
temperatura; assim a viscosidade dos gases aumenta com a
temperatura;
Apesar da viscosidade dos líquidos e gases aumentarem
ligeiramente com a pressão, o aumento é insignificante num
intervalo de pressões considerável; assim, a viscosidade
absoluta dos gases e líquidos é usualmente considerada
independente da pressão;

31. 2.4- Fluidos Newtonianos e não-Newtonianos
Os fluidos classificados como newtonianos, sejam eles mais ou menos
viscosos, caracterizam-se por terem uma viscosidade constante, ou seja,
seguem a Lei de Newton da viscosidade. São exemplos a água, o leite, os
óleos vegetais, etc. Já nos fluidos não-newtonianos a viscosidade varia com
a força aplicada (e por vezes com o tempo também) e portanto têm
propriedades mecânicas muito interessantes.
Um bom exemplo é o ketchup. Quando o frasco está em repouso o ketchup
é muito viscoso, mas quando o inclina ele torna-se menos viscoso e escorre,
e ainda, quando o mete na boca não sente a viscosidade.e ainda, quando o mete na boca não sente a viscosidade.
O exemplo da mistura de amido e água é muito fácil de ser realizada em
nossa própria casa; uma vez obtida a mistura comprovaremos um fato
insólito: ao agitá-la lentamente comporta-se como um fluído semi-líquido,
mas ao agitá-la com força se mostra dura como uma pedra. Enquanto se
mexe devagar com uma colher, a mistura terá a textura de uma papinha,
mas tente dar um soco e seus dedos toparão com algo tão sólido quanto
uma parede.
Em resumo, de uma forma simplificada, podemos dizer que os fluidos não-
newtonianos não possuem uma viscosidade bem definida.
31

32. 32

33. ττ
Taxa de deformação
33

34. A reologia é o ramo da mecânica dos fluidos que estuda as propriedades
físicas que influenciam o transporte de quantidade de movimento num
fluido. É o ramo da física que estuda a viscosidade, plasticidade,
elasticidade e o escoamento da matéria.
Podemos então concluir que é a ciência responsável pelo estudo do fluxo e
deformações decorrentes deste fluxo, envolvendo a fricção do fluido.
A viscosidade é a propriedade reológica mais conhecida, e a única que
caracteriza os fluidos newtonianos.
A viscosidade aparente, µµµµ , é a viscosidade dos fluidos não-Newtonianos, aA viscosidade aparente, µµµµap , é a viscosidade dos fluidos não-Newtonianos, a
qual é válida para uma determinada taxa de deformação. Em fluido
Newtonianos a idêntica a µµµµ.
A viscosidade aparente diminui com o aumento da taxa de deformação em
fluidos pseudoplásticos (tornam-se mais finos quando sujeitos a tensões de
cisalhamento).
Os fluidos nos quais a viscosidade aparente cresce conforme a taxa de
deformação aumenta, são chamados de dilatantes (tornam-se mais espessos
quando sujeito a tensões de cisalhamento). 34

35. Numerosas equações empíricas têm sido propostas para descrever os
fluidos não-newtonianos independentes do tempo. Para muitas aplicações
da engenharia, essas relações podem ser adequadamente representadas
pelo exponencial que, para o escoamento unidimensional, torna-se:
dy
dv
k
n
x
yx 





=τ
onde o expoente, n, é chamado de índice de comportamento do escoamento
e o coeficiente, k, é o índice de consistência. Essa equação reduz-se à lei de
µµ ττ
e o coeficiente, k, é o índice de consistência. Essa equação reduz-se à lei de
Newton da viscosidade para n = 1 e k = µµµµ. Para assegurar que ττττyx tenha o
mesmo sinal de dvx/dy, a equação anterior é reescrita na forma:
dy
dv
dy
dv
dy
dv
k
dy
dv
dy
dv
dy
dv
k x
ap
x
1n
xx
1
x
n
x
yx
ap
µτ
µ
=





=











=
−−
43421
onde µµµµap é referenciado como viscosidade aparente do fluido.
35

36. Esquema de classificação dos fluidos conforme o comportamento reológico:
Um fluido que se comporta como um sólido até que uma tensão limítrofe, ττττy , seja
excedida e exibe uma relação linear entre tensão de cisalhamento e taxa de
deformação é denominado plástico de Bingham ou plástico ideal. O modelo
correspondente de cisalhamento é:
dy
dvx
apyyx µττ +=
36

37. Existem materiais que se comportam parcialmente como um
fluido e parcialmente como um sólido. Estes são os fluidos
viscoelásticos.
Os fluidos viscoelásticos tem algumas características, tais como:
- o tensor extra de tensões não é mais uma função linear, mas
descrevem efeitos viscosos e elásticos do escoamento do fluidodescrevem efeitos viscosos e elásticos do escoamento do fluido
em questão;
- a viscosidade normalmente é muito maior do que a dos fluidos
newtonianos;
- a viscosidade é dependente da temperatura.
37

38. Viscoelásticos
(propriedades elásticas
e viscosas acopladas)
Modelo Maxwell
(propriedades elásticas)
Modelo Kelvin-Voigt
(propriedades viscosas)
Estas substâncias quando
submetidas à tensão de
cisalhamento sofrem uma
deformação e quando cessa,
ocorre uma certa recuperação
da deformação sofrida
Massas de farinha de trigo,
gelatinas, queijos, líquidos
poliméricos, glicerina,
plasma, biopolímeros,
saliva, etc.
Dependente do tempo
Reopético
A viscosidade aparente diminui
conforme a duração da tensão
Alguns lubrificantes,
suspensão de pentóxido de
vanádio e argila bentonita.
Tixotrópico
A viscosidade aparente aumenta
conforme a duração da tensão
Suspensões concentradas,
emulsões, soluções
protéicas, petróleo cru,
Comparativo de propriedades de fluidos não newtonianos:
conforme a duração da tensão protéicas, petróleo cru,
tintas, ketchup.
Independente do
tempo
Pesudoplástico
A viscosidade aparente diminui
conforme o aumento da tensão
de cisalhamento .
Polpa de frutas, caldos de
fermentação, melaço de
cana.
Dilatante
A viscosidade aparente aumenta
conforme a duração da tensão
de cisalhamento .
Suspensões de amido,
soluções de farinha de milho
e açúcar, silicato de potássio
e areia.
Plásticos de Bingham
Este tipo de fluido apresenta
uma relação linear entre a
tensão de cisalhamento e a taxa
de deformação.
Fluidos de perfuração de
poços de petróleo, pasta
dental, maionese, mel, etc.
Herschel-Bulkley
A relação entre a tensão de
cisalhamento e a taxa de
deformação não é linear.
Sangue, iogurte, purê de
tomate, etc.
38

39. Fluido Herschel-Bulkley:
Esses fluidos apresentam o comportamento do tipo lei da
potência com tensão de cisalhamento inicial. É o modelo mais
geral.
dv
n
x




+= µττ
39
escoamentodeindicen
dy
dvx
apyyx
=






+= µττ

40. Classificados em dois grupos: primário e secundário
Determinação simultânea da tensão de cisalhamento e taxa de
deformação num mesmo ponto do aparelho de medição
Há viscosímetros: rotacionais e capilares.
Instrumentos que realizam medidas
diretas da tensão e da taxa de deformação
2.5- Determinação experimental de propriedades reológicas
do fluido;
De disco, de cone-disco e o de cilindro
rotativo;
Todos eles visando a reprodução do
escoamento entre placas planas paralelas.
Podem ser aplicados para ensaios tanto
de fluidos Newtonianos como de fluidos
com comportamento tensão versus
deformação não-linear e/ou visco-elástico.
Primários

41. Esquema de viscosímetros primários
µ = viscosidade;
Ω = velocidade angular aplicada
α = ângulo do cone
R = raioR = raio
B = distância;
T = torque medido, que resulta da tensão
oriunda da deformação do fluido.

42. Viscosímetro primário de Brookfield
muito popular pela facilidade de manuseio.
"spindles" cada um apropriado"spindles" cada um apropriado
para medir a viscosidade de fluidos
em uma faixa específica: os de menor
diâmetro, as maiores viscosidades; os
de maior diâmetro, as menores
viscosidades.

43. Inferem a razão entre a tensão aplicada e a
taxa de deformação por meios indiretos, sem
medir a tensão e deformação diretamente;
aplicam-se somente a fluidos Newtonianos,
por medirem a viscosidade indiretamente.
Secundários
por medirem a viscosidade indiretamente.
Viscosímetro capilar e viscosímetro de
Stokes.

44. A viscosidade é obtida através
de medições do tempo de
queda livre de uma esfera
através de um fluido
estacionário.
Viscosímetro de Stokes
g = aceleração da gravidade
D = diâmetro da esfera
ρρρρs = densidade da esfera
ρρρρf = densidade do fluido
V = velocidade terminal de queda livre, isto é, a razão entre a distância L e o intervalo
de tempo ∆∆∆∆t.
* Esta relação aplica-se somente para esferas em queda livre em meio infinito, com
Reynolds menores do que 1.

45. Viscosímetro Capilar
A viscosidade é obtida por meio da
medida do gradiente de pressão de um
escoamento laminar em um tubo.
Q = vazão volumétrica
L = distância entre as tomadas de pressão
∆∆∆∆P = diferença de pressão
D = diâmetro do tubo capilar

46. Fácil manuseio;
A viscosidade está relacionada com o
tempo de esvaziamento de um copo de
volume conhecido que tem um orifício
calibrado na sua base;
Conjunto de orifícios-padrão (giglê)
feitos de bronze polido
Viscosímetro Copo Ford
feitos de bronze polido
O orifícios de número 2, 3 e 4 são
utilizados para medir líquidos de baixa
viscosidade, na faixa de 20 a 310
centistokes;
Os orifícios de número 5, 6, 7 e 8 para
líquidos de viscosidade superior a 310 cSt.

47. 2.5- Algumas propriedades dos fluidos
2.5.1- Massa específica
A massa específica de uma substância, designada por ρρρρ , é definida como a
massa de uma substância contida numa unidade de volume. Esta
propriedade é normalmente utilizada para caracterizar a massa de um
sistema fluido.
etc.;
L
kg
;
cm
g
;
m
kg
V
m
33 


=ρ
2.5.2- Volume específico
O volume específico, νννν , é o volume ocupado por uma unidade de massa da
substância considerada. Note que o volume específico é o recíproco da
massa específica, ou seja:
Normalmente não é utilizado o volume específico na mecânica dos fluidos,
mas é uma propriedade muito utilizada na termodinâmica.
etc.;
kg
L
;
g
cm
;
kg
m1 33






=
ρ
ν
47

48. 2.5.3- Peso específico
O peso específico de uma substância, designada por γγγγ , é definido como o
peso da substância contida numa unidade de volume. O peso específico está
relacionado com a massa específica através da relação:
onde g é a aceleração da gravidade padrão (9,807 m/s2). Note que o peso
específico é utilizado para caracterizar o peso do sistema fluido enquanto
que a massa específica é utilizada para caracterizar a massa do sistema
fluido.



= etc.;
ft
lbf
;
cm
dina
;
m
N
ρ.gγ 333
fluido.
2.5.4- Densidade relativa
A densidade relativa de um fluido, designada por SG ( specific gravity ), é
definida como a razão entre a massa específica do fluido e a massa
específica da água a 4°°°°C (ρρρρágua = 1000 kg/m3). Nesta condição, temos:
( Adimensional )
ρ
ρ
SG
C4aágua
fluido
fluido
0
=
48

49. 2.6- Lei dos gases perfeitos
Os gases são muito mais compressíveis do que os líquidos. Sob certas
condições, a massa específica de uma gás está relacionada com a pressão e a
temperatura através da equação:
ρRTRT
V
m
PM
perfeitos)gasesdos(leiRT
M
m
nRTPV
==
==
.atm/mol.Kcm82,05R
absolutaratemperatuT
ideaisgasesdosuniversalconstanteR
gásdomolarmassaM
gásdoabsolutaPressãoP
RT
PM
ρ
ρRTRT
V
PM
3
=







=
=
=
=
=
==
49