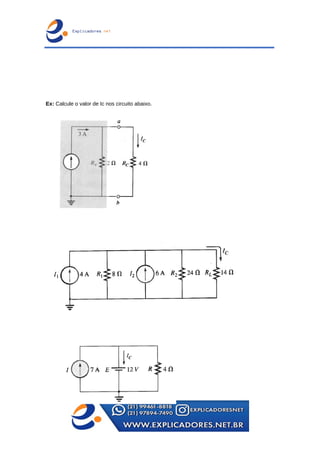
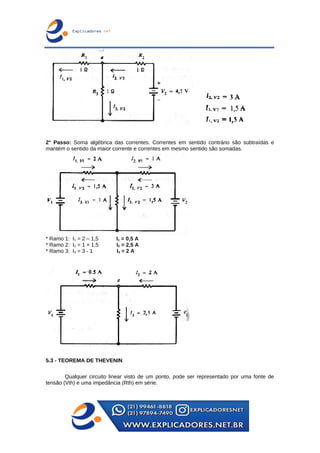
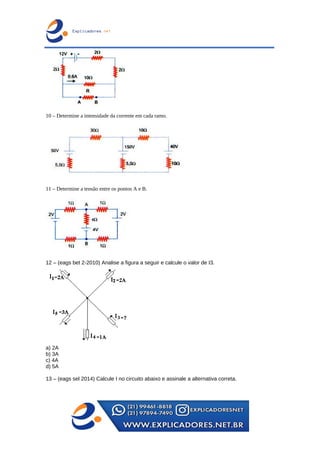
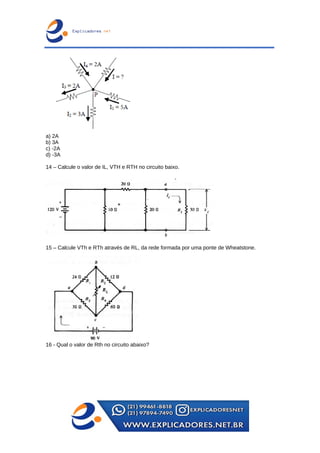
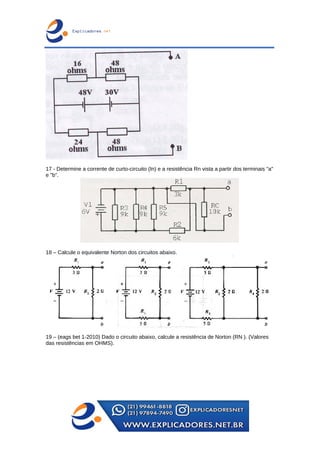
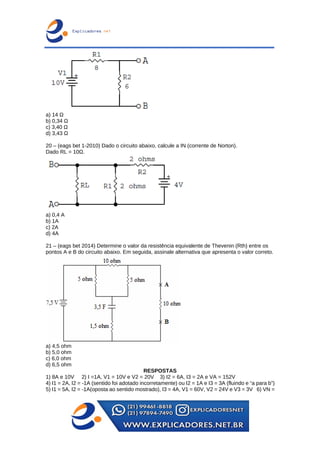
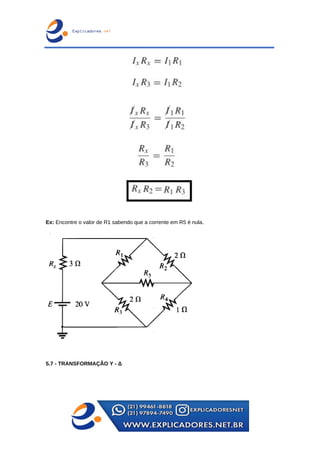
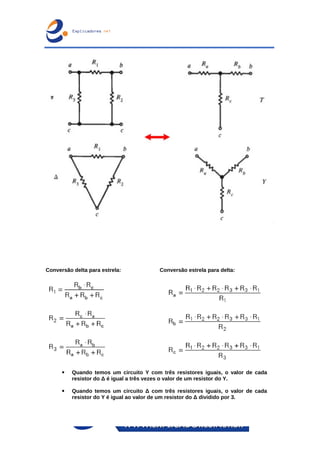
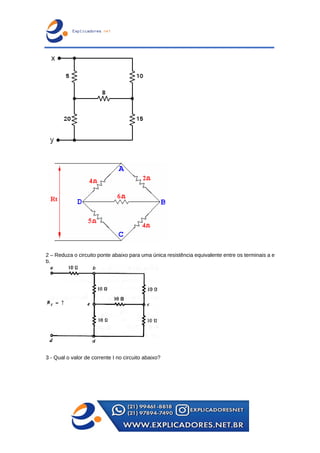
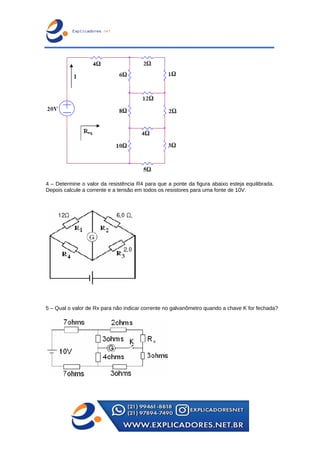
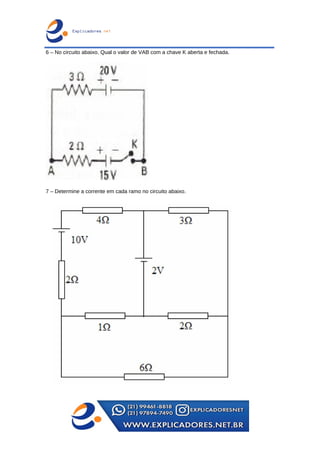
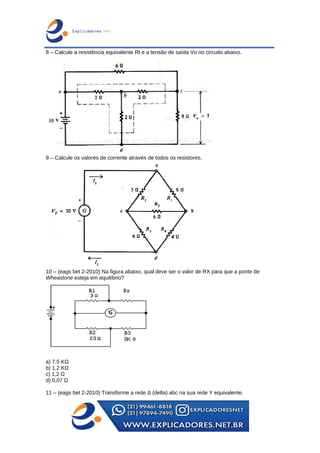
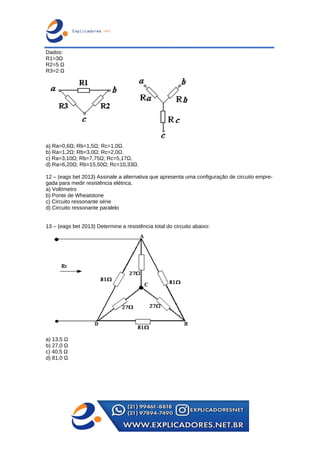
O documento trata dos principais teoremas para análise de circuitos elétricos, incluindo fontes de corrente e tensão, teoremas de superposição, de Thevenin e de Norton, além das leis de Kirchhoff. Apresenta exemplos passo a passo para o cálculo de tensões e correntes em circuitos e aborda a ponte de Wheatstone e transformações entre configurações de circuito. Contém exercícios para aplicação dos conceitos apresentados.

1. 5 – TEOREMAS PARA ANÁLISE DE CIRCUITOS
5.1 – FONTES DE CORRENTES
Enquanto as fontes de tensão apresentam um valor fixo de tensão em seus terminais variando a
corrente de acordo com a carga conectada a elas as fontes de corrente mantém o valor fixo de
corrente no ramo que estejam conectadas variando o valor da tensão de acordo com a carga.
Fonte de corrente real – resistência interna muito alta em paralelo
Fonte de corrente Ideal - resistência interna infinita
EX: Calcule o valor da corrente e da tensão nos terminais do resistor R1.
Conversões de fonte

2. Ex: Calcule o valor de Ic nos circuito abaixo.

3. 5.2 TEOREMA DA SUPERPOSIÇÃO
Em um circuito com mais de uma fonte, a corrente ou a tensão para qualquer
componente é igual à soma algébrica das correntes ou tensões produzidas por cada fonte
isoladamente.
Ex: Calcule a corrente nos ramos do circuito abaixo.
1° passo: Calcularemos as correntes no circuito com todas as fontes separadamente. Para isso
eliminamos todas as fontes do circuito e deixaremos apenas uma para o cálculo das correntes.
Para cada fonte de tensão ideal substituímos por um curto-circuito e para fonte de corrente ideal
substituímos por um circuito aberto.
* Fonte de 3V (lateral):
* Fonte de 4,5V:

4. 2° Passo: Soma algébrica das correntes. Correntes em sentido contrário são subtraídas e
mantém o sentido da maior corrente e correntes em mesmo sentido são somadas.
* Ramo 1: I1 = 2 – 1,5 I1 = 0,5 A
* Ramo 2: I2 = 1 + 1,5 I2 = 2,5 A
* Ramo 3: I3 = 3 - 1 I3 = 2 A
5.3 - TEOREMA DE THEVENIN
Qualquer circuito linear visto de um ponto, pode ser representado por uma fonte de
tensão (Vth) e uma impedância (Rth) em série.

5. EX: Encontre a corrente que percorre o resistor de 3,6Ω.
1° passo - cálculo de Vth: Retire o resistor de 3,6Ω do circuito e calcule a tensão nos pontos a e
b. Note que a tensão entre os terminas a e b é a mesma tensão no resistor R2.
2° passo - cálculo de Rth: Coloque todas as fontes em zero, curto-circuito nas fontes de tensão
e circuito aberto nas fontes de corrente, e calcule a resistência total nos pontos a e b.
3° Passo: Colocar Vth, Rth e a resistência de 3,6Ω em série e calcule sua corrente.

6. 5.4 - TEOREMA DE NORTON
Uma rede que contenha fonte de tensão e elementos passivos pode ser substituída por
uma única fonte de corrente (In) em paralelo com uma impedância (Rn).
Ex: Utilizando o circuito do exemplo do teorema de Thevenin, temos:
1° passo – Cálculo de IN: Colocamos um curto circuito entre os pontos a e b. A corrente IN
também é chamada de corrente de curto circuito.

7. 2° passo – Cálculo de RN: A resistência RN é calculada da mesma forma que Rth.
3° passo: Montamos o circuito equivalente Norton e calculamos a corrente no resistor RL.
5.5 - LEIS DE KIRCHHOFF
Lei das malhas - A soma das tensões em uma malha e igual a zero.
Lei do nós - A soma das correntes que entram em um nó, é igual à soma das correntes que
saem de um nó.
Resolução de circuitos pelas leis de Kirchhoff

8. 1° passo: Marcar os vértices e os nós das malhas.
2° passo: Convencionar os sentidos das correntes.
3° passo: Marcar a polaridade dos resistores (O positivo e onde entra a corrente e negativo e
onde sai a corrente).
40
passo: Encontrar as equações das malhas de acordo com a lei das malhas.
Equação 2 (Malha ABEFA):
0,5I1 – 0,5I2 + 0,5I1 + 20 – 0,5I2 + 0,5I1 + I1 - 20 + 0,5I1 = 0
– I2 + 3I1= 0
Equação 3 (Malha BCDEB):
4I2 + 6 + 0,5I2 – 0,5I1 – 20 + 0,5I2 – 0,5I1 = 0
5I2 - I1 = 14
5° passo: Separamos as equações. Multiplicamos todos os elementos de uma das equações
de forma que possamos eliminar uma das incógnitas depois que somarmos as duas equações.
– I2 + 3I1= 0
5I2 - I1 = 14 (3)
6° passo: efetuamos a soma das equações.

9. – I2 + 3I1= 0
+
15I2 - 3I1 = 42
14I2 = 42
I2 = 3A
7° passo: Substituímos I2 nas outras. equações.
– I2 + 3I1= 0
-3 + 3I1= 0
3I1= 3
I1 = 1A
80
Encontre a corrente resultante no centro do circuito.
I3 = I2 – I1
I3 = 3 – 1
I3 = 2A
EXERCÍCIOS
1 – Calcule as quantidades desconhecidas indicadas nas figuras abaixo.
2 - Calcule a corrente e as quedas de tensão através de R1 e R2.
3 – Calcule I2, I3 e IA.

10. 4 – Calcule a corrente em cada resistor.
5 – Calcule todas as correntes e as quedas de tensão no circuito abaixo.
6 – Qual o valor da tensão VN?

11. 7 - (VUNESP) O amperímetro A indicado no circuito abaixo é ideal, isto é, tem resistência praticamente
nula. Os fios de ligação têm resistência desprezível. Qual a intensidade de corrente elétrica indicada no
amperímetro A é de:
8 – No circuito abaixo, qual o valor de tensão entre os pontos Q e P?
9 – Qual o valor de resistência deve ser colocado nos pontos A e B para que no resistor de 10Ω passe uma
corrente de 0,6A?

12. 10 – Determine a intensidade da corrente em cada ramo.
11 – Determine a tensão entre os pontos A e B.
12 – (eags bet 2-2010) Analise a figura a seguir e calcule o valor de I3.
a) 2A
b) 3A
c) 4A
d) 5A
13 – (eags sel 2014) Calcule I no circuito abaixo e assinale a alternativa correta.

13. a) 2A
b) 3A
c) -2A
d) -3A
14 – Calcule o valor de IL, VTH e RTH no circuito baixo.
15 – Calcule VTh e RTh através de RL, da rede formada por uma ponte de Wheatstone.
16 - Qual o valor de Rth no circuito abaixo?

14. 17 - Determine a corrente de curto-circuito (In) e a resistência Rn vista a partir dos terminais "a"
e "b".
18 – Calcule o equivalente Norton dos circuitos abaixo.
19 – (eags bet 1-2010) Dado o circuito abaixo, calcule a resistência de Norton (RN ). (Valores
das resistências em OHMS).

15. a) 14 Ω
b) 0,34 Ω
c) 3,40 Ω
d) 3,43 Ω
20 – (eags bet 1-2010) Dado o circuito abaixo, calcule a IN (corrente de Norton).
Dado RL = 10Ω.
a) 0,4 A
b) 1A
c) 2A
d) 4A
21 – (eags bet 2014) Determine o valor da resistência equivalente de Thevenin (Rth) entre os
pontos A e B do circuito abaixo. Em seguida, assinale alternativa que apresenta o valor correto.
a) 4,5 ohm
b) 5,0 ohm
c) 6,0 ohm
d) 6,5 ohm
RESPOSTAS
1) 8A e 10V 2) I =1A, V1 = 10V e V2 = 20V 3) I2 = 6A, I3 = 2A e VA = 152V
4) I1 = 2A, I2 = -1A (sentido foi adotado incorretamente) ou I2 = 1A e I3 = 3A (fluindo e “a para b”)
5) I1 = 5A, I2 = -1A(oposta ao sentido mostrado), I3 = 4A, V1 = 60V, V2 = 24V e V3 = 3V 6) VN =

16. 3,75V 7) 2A 8) 11V 9) 15 ohms 10) 2A, 6A e 4A 11) 2,4V 12) c 13) c 14) RTh = 10Ω, VTh
= 60V e IL = 1,5A 15) VTh = 28Ω e VTh = 30V 16) RTh = 28 e VTh = 6,5V 17) IN = 1mA e
VN = 2kΩ 18) IN = 4A, RN = 1,2 Ω, IN = 1,5A, RN = 1,6 Ω, 1,5A, RN = 0,89V 19) d 20) c 21) b
5.6 PONTE DE WHEATSTONE
Circuito utilizado para medir valores de resistências utilizando uma fonte de tensão e três
resistores de valores conhecidos.
A ponte esta equilibrada, quando a corrente que passa pelo galvanômetro for nula. Isso
ocorre quando o potenciômetro R3 é ajustado para que não exista diferença de potencial entre os
pontos b e c.

17. Ex: Encontre o valor de R1 sabendo que a corrente em R5 é nula.
5.7 - TRANSFORMAÇÃO Y - Δ

18. Conversão delta para estrela: Conversão estrela para delta:
 Quando temos um circuito Y com três resistores iguais, o valor de cada
resistor do Δ é igual a três vezes o valor de um resistor do Y.
 Quando temos um circuito Δ com três resistores iguais, o valor de cada
resistor do Y é igual ao valor de um resistor do Δ dividido por 3.

19. Ex: Converta o circuito abaixo de delta para estrela.
Ex: converta o circuito abaixo de estrela para delta.
Exercícios
1 – Qual o valor da resistência equivalente dos circuitos abaixo.

20. 2 – Reduza o circuito ponte abaixo para uma única resistência equivalente entre os terminais a e
b.
3 - Qual o valor de corrente I no circuito abaixo?

21. 4 – Determine o valor da resistência R4 para que a ponte da figura abaixo esteja equilibrada.
Depois calcule a corrente e a tensão em todos os resistores para uma fonte de 10V.
5 – Qual o valor de Rx para não indicar corrente no galvanômetro quando a chave K for fechada?

22. 6 – No circuito abaixo, Qual o valor de VAB com a chave K aberta e fechada.
7 – Determine a corrente em cada ramo no circuito abaixo.

23. 8 – Calcule a resistência equivalente Rt e a tensão de saída Vo no circuito abaixo.
9 – Calcule os valores de corrente através de todos os resistores.
10 – (eags bet 2-2010) Na figura abaixo, qual deve ser o valor de RX para que a ponte de
Wheastone esteja em equilíbrio?
a) 7,5 KΩ
b) 1,2 KΩ
c) 1,2 Ω
d) 0,07 Ω
11 – (eags bet 2-2010) Transforme a rede Δ (delta) abc na sua rede Υ equivalente.

24. Dados:
R1=3Ω
R2=5 Ω
R3=2 Ω
a) Ra=0,6Ω; Rb=1,5Ω; Rc=1,0Ω.
b) Ra=1,2Ω; Rb=3,0Ω; Rc=2,0Ω.
c) Ra=3,10Ω; Rb=7,75Ω; Rc=5,17Ω.
d) Ra=6,20Ω; Rb=15,50Ω; Rc=10,33Ω.
12 – (eags bet 2013) Assinale a alternativa que apresenta uma configuração de circuito empre-
gada para medir resistência elétrica.
a) Voltímetro
b) Ponte de Wheatstone
c) Circuito ressonante série
d) Circuito ressonante paralelo
13 – (eags bet 2013) Determine a resistência total do circuito abaixo:
a) 13,5 Ω
b) 27,0 Ω
c) 40,5 Ω
d) 81,0 Ω

25. RESPOSTAS
1) 12,16 ohms, 3,59 ohms 2) 20 ohms 3) 1,64A 4) R4 = 4 ohms, IR1 = IR2 = 0,56A, IR3 = IR4
= 1,67A, VR1 = VR4 = 6,72V, VR2 = VR3 = 3,36V 5) Rx = 4,5 ohms 6) Chave fechada = 17V,
Chave aberta = 20V
7) 1,2A, 0,5A, 0,7A, 0,8A, 0,25A e 0,21A 8) 3 ohms e 5V 9) IR1 = 2A, IR2 = 4A, IR3 = 1A, IR4 =
3A e IR5 = 3A 10) b 11) a 12) b 13) b