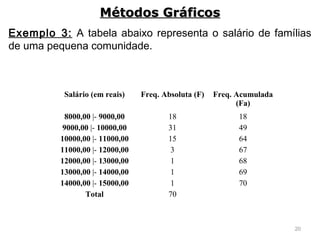
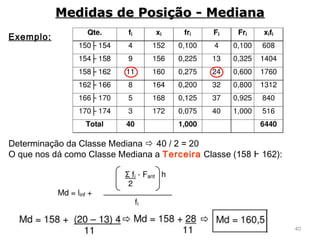
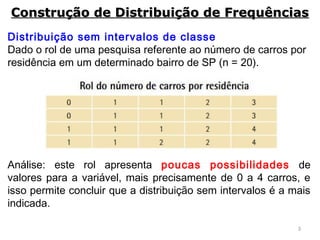
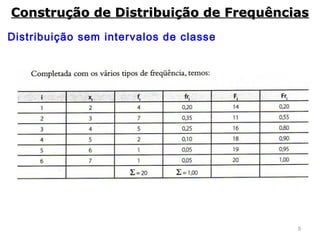
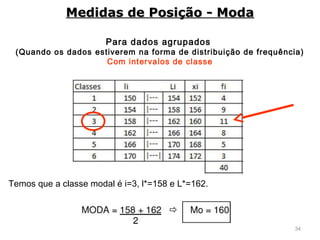
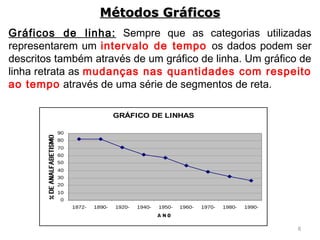
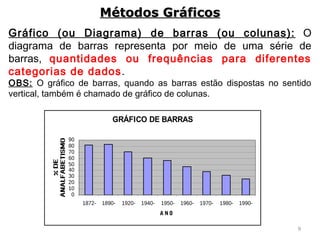
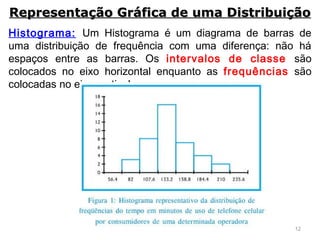
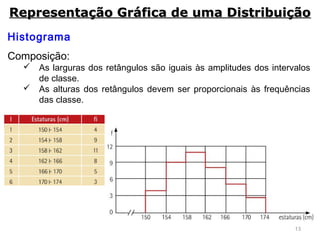
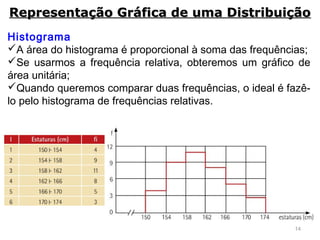
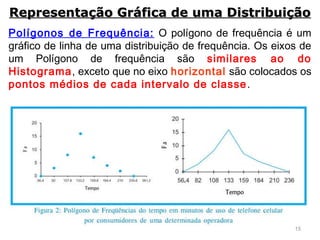
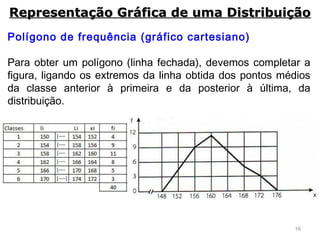
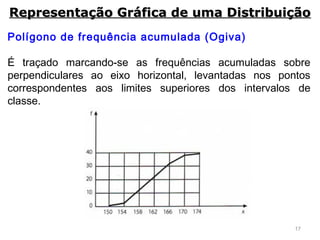
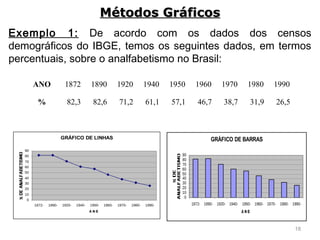
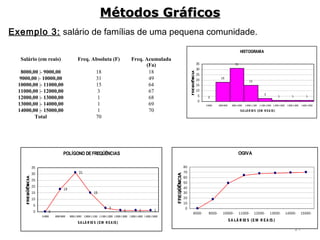
1) O documento discute métodos estatísticos para análise de dados, incluindo distribuição de frequência, medidas de posição e representação gráfica. 2) São apresentados diferentes tipos de distribuição de frequência como distribuição sem intervalos de classe e métodos para construí-las. 3) São descritos vários métodos gráficos como histograma, polígono de frequências e gráfico de setores que podem ser usados para representar distribuições de frequência e dados estatísticos.

1. 1Profa.M.a Ecila Alves de Oliveira MiglioriProfa.M.a Ecila Alves de Oliveira Migliori
Distribuição de FrequênciaDistribuição de Frequência
Terceira Aula

2. 2
Quando se trata de variável discreta de variação
relativamente pequena, cada valor pode ser tomado como um
intervalo de classe (intervalo degenerado) e, nesse caso, a
distribuição é chamada distribuição sem intervalos de
classe.
Construção de Distribuição de FrequênciasConstrução de Distribuição de Frequências

3. 3
Distribuição sem intervalos de classe
Dado o rol de uma pesquisa referente ao número de carros por
residência em um determinado bairro de SP (n = 20).
Análise: este rol apresenta poucas possibilidades de
valores para a variável, mais precisamente de 0 a 4 carros, e
isso permite concluir que a distribuição sem intervalos é a mais
indicada.
Construção de Distribuição de FrequênciasConstrução de Distribuição de Frequências

4. 4
Distribuição sem intervalos de classe
A partir do rol, basta colocar em cada classe um dos valores da
variável e contar o número de ocorrências para cada classe.
Construção de Distribuição de FrequênciasConstrução de Distribuição de Frequências

5. 5
Distribuição sem intervalos de classe
Construção de Distribuição de FrequênciasConstrução de Distribuição de Frequências

6. Métodos GráficosMétodos Gráficos
6

7. 7
Objetivo:Facilitar a compreensão do fenômeno estatístico por
meio do efeito visual imediato que lhe é próprio.
Tipos de Gráficos mais usados:
•Gráficos de linha
•Diagramas de área:
•Gráficos de coluna;
•Gráficos de barras;
•Gráficos de setores (ou gráfico de Pizza).
•Representação gráfica para as distribuições de frequências:
•Histograma
•Polígono de frequências;
•Polígono de frequências acumulada (Ogiva).
Métodos GráficosMétodos Gráficos

8. 8
Gráficos de linha: Sempre que as categorias utilizadas
representarem um intervalo de tempo os dados podem ser
descritos também através de um gráfico de linha. Um gráfico de
linha retrata as mudanças nas quantidades com respeito
ao tempo através de uma série de segmentos de reta.
Métodos GráficosMétodos Gráficos
GRÁFICO DE LINHAS
0
10
20
30
40
50
60
70
80
90
1872- 1890- 1920- 1940- 1950- 1960- 1970- 1980- 1990-
A N O

9. 9
Gráfico (ou Diagrama) de barras (ou colunas): O
diagrama de barras representa por meio de uma série de
barras, quantidades ou frequências para diferentes
categorias de dados.
OBS: O gráfico de barras, quando as barras estão dispostas no sentido
vertical, também é chamado de gráfico de colunas.
Métodos GráficosMétodos Gráficos
GRÁFICO DE BARRAS
0
10
20
30
40
50
60
70
80
90
1872- 1890- 1920- 1940- 1950- 1960- 1970- 1980- 1990-
A N O

10. 10
Gráfico (ou Diagrama) de setores: O diagrama de
setores, também conhecido como gráfico de Pizza, é uma
gráfico particularmente apropriado para representar as
divisões de um montante total.
Métodos GráficosMétodos Gráficos

11. 11
Uma distribuição de frequência pode ser representada
graficamente pelo histograma, pelo polígono de
frequência e pelo polígono de frequência acumulada.
Representação Gráfica de uma DistribuiçãoRepresentação Gráfica de uma Distribuição

12. 12
Histograma: Um Histograma é um diagrama de barras de
uma distribuição de frequência com uma diferença: não há
espaços entre as barras. Os intervalos de classe são
colocados no eixo horizontal enquanto as frequências são
colocadas no eixo vertical.
Representação Gráfica de uma DistribuiçãoRepresentação Gráfica de uma Distribuição

13. 13
Histograma
Composição:
 As larguras dos retângulos são iguais às amplitudes dos intervalos
de classe.
 As alturas dos retângulos devem ser proporcionais às frequências
das classe.
Representação Gráfica de uma DistribuiçãoRepresentação Gráfica de uma Distribuição

14. 14
Histograma
A área do histograma é proporcional à soma das frequências;
Se usarmos a frequência relativa, obteremos um gráfico de
área unitária;
Quando queremos comparar duas frequências, o ideal é fazê-
lo pelo histograma de frequências relativas.
Representação Gráfica de uma DistribuiçãoRepresentação Gráfica de uma Distribuição

15. 15
Polígonos de Frequência: O polígono de frequência é um
gráfico de linha de uma distribuição de frequência. Os eixos de
um Polígono de frequência são similares ao do
Histograma, exceto que no eixo horizontal são colocados os
pontos médios de cada intervalo de classe.
Representação Gráfica de uma DistribuiçãoRepresentação Gráfica de uma Distribuição

16. 16
Polígono de frequência (gráfico cartesiano)
Para obter um polígono (linha fechada), devemos completar a
figura, ligando os extremos da linha obtida dos pontos médios
da classe anterior à primeira e da posterior à última, da
distribuição.
Representação Gráfica de uma DistribuiçãoRepresentação Gráfica de uma Distribuição

17. 17
Polígono de frequência acumulada (Ogiva)
É traçado marcando-se as frequências acumuladas sobre
perpendiculares ao eixo horizontal, levantadas nos pontos
correspondentes aos limites superiores dos intervalos de
classe.
Representação Gráfica de uma DistribuiçãoRepresentação Gráfica de uma Distribuição

18. 18
Exemplo 1: De acordo com os dados dos censos
demográficos do IBGE, temos os seguintes dados, em termos
percentuais, sobre o analfabetismo no Brasil:
Métodos GráficosMétodos Gráficos
ANO 1872 1890 1920 1940 1950 1960 1970 1980 1990
% 82,3 82,6 71,2 61,1 57,1 46,7 38,7 31,9 26,5
GRÁFICO DE LINHAS
0
10
20
30
40
50
60
70
80
90
1872- 1890- 1920- 1940- 1950- 1960- 1970- 1980- 1990-
A N O
GRÁFICO DE BARRAS
0
10
20
30
40
50
60
70
80
90
1872- 1890- 1920- 1940- 1950- 1960- 1970- 1980- 1990-
A NO

19. 19
Exemplo 2: De 75.200 mortes por acidentes nos EUA, em um
ano recente, 43.500 foram causadas por veículos motorizados,
12.200 por quedas, 6.400 por envenenamento, 4.600 por
afogamento, 4.200 por incêndios, 2.900 por ingestão de
alimentos ou de um objeto, e 1.400 por armas de fogo (com
base em dados do Conselho de Segurança Nacional).
Descrever estes dados através de um gráfico de setores.
Métodos GráficosMétodos Gráficos

20. 20
Exemplo 3: A tabela abaixo representa o salário de famílias
de uma pequena comunidade.
Métodos GráficosMétodos Gráficos
Salário (em reais) Freq. Absoluta (F) Freq. Acumulada
(Fa)
8000,00 |- 9000,00 18 18
9000,00 |- 10000,00 31 49
10000,00 |- 11000,00 15 64
11000,00 |- 12000,00 3 67
12000,00 |- 13000,00 1 68
13000,00 |- 14000,00 1 69
14000,00 |- 15000,00 1 70
Total 70

21. 21
Exemplo 3: salário de famílias de uma pequena comunidade.
Métodos GráficosMétodos Gráficos
Salário (em reais) Freq. Absoluta (F) Freq. Acumulada
(Fa)
8000,00 |- 9000,00 18 18
9000,00 |- 10000,00 31 49
10000,00 |- 11000,00 15 64
11000,00 |- 12000,00 3 67
12000,00 |- 13000,00 1 68
13000,00 |- 14000,00 1 69
14000,00 |- 15000,00 1 70
Total 70
HISTOGRAMA
0
18
31
15
3
1 1 1
0
5
10
15
20
25
30
35
0-8000 8000-9000 9000-10000 10000-11000 11000-12000 12000-13000 13000-14000 14000-15000
SA LÁ R IO S (EM R EA IS)
POLÍGONO DEFREQÜÊNCIAS
0
18
31
15
3
1 1 10
5
10
15
20
25
30
35
0-8000 8000-9000 9000-10000 10000-11000 11000-12000 12000-13000 13000-14000 14000-15000
SA LÁ R IO S (EM R EA IS)
OGIVA
0
10
20
30
40
50
60
70
80
8000- 9000- 10000- 11000- 12000- 13000- 14000- 15000-
SA LÁ R IO S (EM R EA IS)

22. Medidas de PosiçãoMedidas de Posição
22

23. 23
Definição: As medidas de posição mais importantes são as
medidas de tendência central, que recebem tal
denominação pelo fato de os dados observados tenderem, em
geral, a se agrupar em torno dos valores centrais.
Dentre as medidas de tendência central, destacamos:
•a média aritmética ( );
•a mediana (Md);
•a moda (Mo).
Três abordagens:
•Dados não agrupados (não alocados em tabelas de frequência);
•Dados agrupados: sem intervalo de classe;
•Dados agrupados: com intervalo de classe.
Medidas de PosiçãoMedidas de Posição
x

24. 24
Média Aritmética : é utilizada para obter a medida de posição que possui
a maior estabilidade.
Para dados não agrupados
(Quando os dados não estiverem na forma de distribuição de
frequência)
Média aritmética simples ( ): é o quociente da divisão da soma dos
valores (dados, observações) da variável pelo número deles:
sendo:
= a média aritmética;
= os valores da variável;
n = o número de valores.
Medidas de PosiçãoMedidas de Posição
x
ix
n
x
x
n
1i
i∑=
=
x

25. 25
Para dados não agrupados
(Quando os dados não estiverem na forma de distribuição de
frequência)
Exemplo: Sabendo-se que a produção leiteira diária da vaca A, durante
uma semana, foi de: 10, 14, 13, 15, 16, 18 e 12 litros, pergunta-se: Encontre
a média para a produção diária de leite desta vaca.
Média:
Logo, = 14 litros de leite em média por dia que representa uma
produção de 98 litros de leite em média por semana.
OBS.: a média pode ser um número diferente de todos os valores da
amostra que ela representa.
Medidas de Posição - MédiaMedidas de Posição - Média
14
7
98
7
12.181615131410
n
x
x
n
1i
i
==
++++++
==
∑=
x

26. 26
Para dados agrupados
(Quando os dados estiverem na forma de distribuição de frequência
com ou sem intervalo de classe)
Nestes casos, como as frequências são números indicadores da
intensidade de cada valor da variável, elas funcionam como fatores de
ponderação, o que nos leva a calcular a Média Aritmética Ponderada,
dada pela fórmula:
Medidas de Posição - MédiaMedidas de Posição - Média
∑
∑
=
=
= n
1i
i
n
1i
ii
f
fx
x

27. 27
Exemplos:
1-) Consideremos a distribuição relativa a 34 famílias de quatro filhos,
tomando para variável o número de filhos do sexo masculino:
Neste caso necessitaremos de uma coluna a mais (xi.fi)
Qual é a média do nº de meninos por família?
Medidas de Posição - MédiaMedidas de Posição - Média
Nº de
meninos
xifi
0 2
1 6
2 10
3 12
4 4
34
if
=∑ if

28. 28
Exemplos:
Média:
Devemos usar a fórmula
já que estamos trabalhando com dados agrupados, assim temos:
= 78 / 34 ≈ 2,29 ≈ 2,3
Medidas de Posição - MédiaMedidas de Posição - Média
Nº de
meninos
xifi
0 2 0
1 6 6
2 10 20
3 12 36
4 4 16
34 78
if
=∑ if
∑
∑
=
=
= n
1i
i
n
1i
ii
f
fx
x
∑
∑
=
=
= n
1i
i
n
1i
ii
f
fx
x

29. 29
Exemplos:
Média ≈ 2,3
Interpretação: Sendo x uma variável discreta, como interpretar o
resultado obtido, 2 filhos e 3 décimos (ou 0,3) de menino?
O valor médio 2,3 meninos sugere, que o maior número de famílias
com 4 filhos tem 2 meninos e 2 meninas, sendo, porém, a tendência geral
de uma leve superioridade numérica em relação ao número de meninos.
Medidas de Posição - MédiaMedidas de Posição - Média
Nº de
meninos
xifi
0 2 0
1 6 6
2 10 20
3 12 36
4 4 16
34 78
if
=∑ if

30. 30
Moda (Mo): É o valor que ocorre com maior frequência em uma série
de valores.
Para dados não agrupados
(Quando os dados não estiverem na forma de distribuição de
frequência)
Basta procurar pelo valor que mais se repete.
Exemplo:
O salário modal dos empregados de uma indústria é o salário mais
comum, isto é, o salário recebido pelo maior número de empregados dessa
indústria.
Medidas de PosiçãoMedidas de Posição

31. 31
Para dados não agrupados
(Quando os dados não estiverem na forma de distribuição de
frequência)
A série de dados:
7, 8, 9, 10, 10, 10, 11, 12, 13 e 15
tem moda igual a 10.
Séries que não apresentam moda são chamadas amodal:
3, 5, 8, 10, 12, 13
Nos casos onde houver dois ou mais valores de concentração para a moda,
a série é chamada bimodal:
2, 3, 4, 4, 4, 5, 6, 7, 7, 7, 8, 9
Medidas de Posição - ModaMedidas de Posição - Moda

32. 32
Para dados agrupados
(Quando os dados estiverem na forma de distribuição de frequência)
Sem intervalos de classe
Uma vez agrupados os dados, é possível determinar imediatamente a
moda: basta fixar o valor da variável de maior frequência.
Mo = 3
Medidas de Posição - ModaMedidas de Posição - Moda
Nº de
meninos
0 2
1 6
2 10
3 12
4 4
34
if
=∑ if

33. 33
Para dados agrupados
(Quando os dados estiverem na forma de distribuição de frequência)
Com intervalos de classe
A classe que apresenta a maior frequência é denominada classe
modal. Pela definição, podemos afirmar que a moda, neste caso, é o valor
dominante que está compreendido entre os limites da classe modal.
O método mais simples para o cálculo da moda consiste em tomar o ponto
médio da classe modal.
Onde l* é o limite inferior da classe modal;
L* é o limite superior da classe modal.
Medidas de Posição - ModaMedidas de Posição - Moda

34. 34
Para dados agrupados
(Quando os dados estiverem na forma de distribuição de frequência)
Com intervalos de classe
Temos que a classe modal é i=3, l*=158 e L*=162.
Medidas de Posição - ModaMedidas de Posição - Moda

35. 35
Mediana (Md): A mediana é outra medida de posição definida como o
número que se encontra no centro de uma série de números, estando
estes dispostos segundo uma ordem.
Em outras palavras, a mediana de um conjunto de valores, ordenados, é o
valor situado de tal forma no conjunto que o separa em dois subconjuntos
de mesmo número de elementos.
Observação:
•Se o nº de elementos for ímpar, então a mediana será exatamente o valor
“do meio”.
•Se o nº de elementos for par, então a mediana será exatamente a média
“dos dois valores do meio”.
Medidas de PosiçãoMedidas de Posição

36. 36
Para dados não agrupados
(Quando os dados não estiverem na forma de distribuição de
frequência)
A série de dados contendo 9 elementos (qtde impar):
5, 13, 10, 2, 18, 15, 6, 16, 9
Ordenados:
2, 5, 6, 9, 10, 13, 15, 16, 18
Valor central: 5º. Elemento = 10
Md = 10
Medidas de Posição - MedianaMedidas de Posição - Mediana

37. 37
Para dados não agrupados
(Quando os dados não estiverem na forma de distribuição de
frequência)
A série de dados contendo 8 elementos (qtde par):
5, 13, 10, 2, 15, 6, 16, 9
Ordenados:
2, 5, 6, 9, 10, 13, 15, 16
Média aritmética simples entre os pontos médios 10 e 13:
Md = (10 + 13)/2 = 11,5
Medidas de Posição - MedianaMedidas de Posição - Mediana

38. 38
Para dados agrupados
(Quando os dados estiverem na forma de distribuição de frequência)
Sem intervalos de classe
Neste caso, é o bastante identificar a frequência acumulada
imediatamente superior à metade da soma das frequências.
A mediana será aquele valor da variável que corresponde a tal frequência
acumulada.
Sendo: 34/2 = 17, logo a Md = 2 meninos
Medidas de Posição - MedianaMedidas de Posição - Mediana
Nº de
meninos
fi
0 2 2
1 6 8
2 10 18
3 12 30
4 4 34
34
if

39. 39
Para dados agrupados
(Quando os dados estiverem na forma de distribuição de frequência)
Com intervalos de classe
Passos para a determinação da Mediana:
1.Determinação da Classe Mediana (é aquela em que a
Mediana está presente).
2.Aplicamos a seguinte fórmula:
Medidas de Posição - MedianaMedidas de Posição - Mediana

40. 40
Exemplo:
Determinação da Classe Mediana  40 / 2 = 20
O que nos dá como Classe Mediana a Terceira Classe (158 162):Ⱶ
Medidas de Posição - MedianaMedidas de Posição - Mediana

41. 41
Exemplo: Sabendo-se que a produção leiteira diária da vaca A, durante
uma semana, foi de: 10, 14, 13, 15, 16, 18 e 12 litros, pergunta-se: Encontre
a moda e a mediana para a produção diária de leite desta vaca.
Moda: Como não existe um valor que aparece com maior frequência que os
outros, não há valor de moda para este exemplo.
Mediana: Ordenando os dados temos:
10 12 13 14 15 16 18
Desta forma, o valor mediano é o valor central dos dados, ou seja,
14 litros de leite por dia.
Medidas de PosiçãoMedidas de Posição

42. 42
Quando uma distribuição é simétrica, as três medidas coincidem:
A assimetria, porém, torna-as diferentes e essa diferença é tanto maior
quanto maior é a assimetria. Assim, em uma distribuição em forma de sino,
temos:
Formas de DistribuiçãoFormas de Distribuição

43. 43
Em um conjunto de dados, a mediana, a moda e a média não
necessariamente devem apresentar o mesmo valor.
Uma informação importante é de que a mediana não é influenciada
pelos valores extremos.
Formas de DistribuiçãoFormas de Distribuição

44. 44
Obrigada.Obrigada.
Resolver a lista de exercícios e entregar na próxima
aula devidamente identificada !!!!
(Nome Completo, RA, Turma)