Este documento apresenta exercícios sobre polígonos regulares e pavimentação do plano com esses polígonos. Na primeira parte, há questões sobre nomes, ângulos e raios de polígonos regulares. A segunda parte trata de pavimentações usando triângulos equiláteros, quadrados e hexágonos, provando que são as únicas figuras possíveis.

1. Resolução das atividades
propostas pelo grupo
ALEPH – extraídas de
http://www.uff.br/cdme/ppr
/ppr-html/ppr-pr-br.html
1

2. PARTE I – POLÍGONOS REGULARES
1) Qual é o nome do polígono regular de 11 lados?
2

3. E o de 27 lados?
3

4. 2) Um quiliógono é um polígono com 1000 lados. Calcule a
medida dos ângulos internos e ângulos centrais de um
quiliógono regular.
n=1000
A medida dos ângulos internos é dada por:
,logo:
A medida dos ângulos centrais é dada por:
, logo:
4

5. Ative as opções “Exibir ângulos internos” e “Exibir ângulos
centrais” do aplicativo. Por que cada ângulo central tem
medida e cada ângulo interno tem medida
5

6. Em um polígono regular de n lados temos n ângulos
centrais. A soma destes ângulos define uma volta completa
na circunferência 360º. Logo, para definirmos a medida de
um ângulo basta dividir 360° por n.
A soma dos ângulos internos de um polígono regular pode
ser definida dividindo-se a figura com segmentos de reta
que ligam cada vértice da figura a cada um dos outros.
Desta forma, o polígono será dividido em n-2
triângulos, cada um com os ângulos internos somando
180°. Assim a somas dos ângulos internos do polígono
será:
Como sabemos que em um polígono regular todos os
ângulos são congruentes, para encontrarmos a medida de
cada ângulo interno basta dividirmos a soma dos ângulos
internos pelo número de lados, então:
6

7. 4) Se R é a medida do raio do círculo circunscrito ao polígono
regular, qual é a medida do raio r do círculo inscrito em
função de R, θ e α?
7

8. Sendo:
R = medida do raio do círculo circunscrito
r = medida do raio do círculo inscrito
= medida do ângulo interno
= medida do ângulo central
Podemos estabeler a relação,
8

9. PARTE II – PAVIMENTAÇÃO DO PLANO COM
POLÍGONOS REGULARES DE UM SÓ TIPO
1) Usando o software, verifique que é possível construir uma
pavimentação lado-lado do plano usando triângulos equiláteros.
Qual é a soma dos ângulos dos triângulos equiláteros com
vértice em um nó da pavimentação?
9

10. A soma dos ângulos dos triângulos eqüiláteros com vértice em um
nó da pavimentação é 360°. Pois, cada ângulo do triângulo
eqüilátero mede 60°, como temos 6 ângulos num mesmo nó,
temos 6 *60°=360°.
10

11. 2) Usando o software, verifique que é possível construir uma
pavimentação lado-lado do plano usando quadrados. Qual é a
soma dos ângulos dos quadrados com vértice em um nó da
pavimentação?
11

12. A soma dos ângulos dos quadrados com vértice em um nó da
pavimentação é 360°. Pois, cada ângulo do quadrado mede 90°,
como temos 4 ângulos num mesmo nó, temos: 4*90°=360°.
12

13. 3) É possível construir uma pavimentação lado-lado do plano
usando pentágonos regulares? Justifique sua resposta!
Não. Pois como podemos ver na figura acima os lados do
pentágono não se encaixam.
13

14. 4) Usando o software, verifique que é possível construir uma
pavimentação lado-lado do plano usando hexágonos
regulares. Qual é a soma dos ângulos dos hexágonos
regulares com vértice em um nó da pavimentação?
14

15. Sabemos que cada ângulo interno de um hexágono regular mede
120°, como o nó da pavimentação é formada por 3
ângulos, temos 3*120º = 360 °.
15

16. 5) O objetivo deste exercício é provar que as únicas
pavimentações lado-lado do plano com polígonos regulares
de um só tipo são aquelas obtidas com triângulos eqüiláteros,
quadrados e hexágonos regulares. Para isto, seja
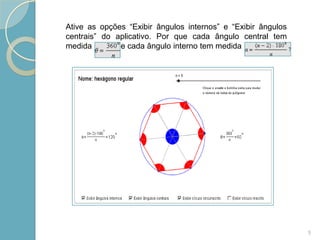
α = (n − 2) 180°/n
a medida dos ângulos internos de um polígono regular com n
lados (veja o Exercício [03] da Parte 1) e seja k o número de
polígonos da pavimentação com um vértice comum. Note que
k α = 360°.
Verifique que k = 2n/(n − 2). Por que k deve ser maior do que
ou igual a 3? Conclua que 2n/(n − 2) ≥ 3 e que, portanto, n ≤
6. Assim, os únicos valores possíveis de n são 3, 4, 5 e 6.
Mas pentágonos regulares não pavimentam o plano
(Exercício [03]), portanto, as únicas pavimentações lado-lado
do plano com polígonos regulares se um só tipo são aquelas
com n = 3, n = 4 e n = 6.
16

17. K tem que ser ≥ 3, pois:
Se K=2, k = 2n/(n − 2) .
, K dá valor negativo, o que descaracteriza a
atividade, uma vez que K representa o número de
polígonos da pavimentação com um vértice em comum.
Nos casos onde , k não representa um número
inteiro.
17