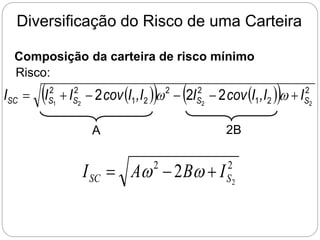
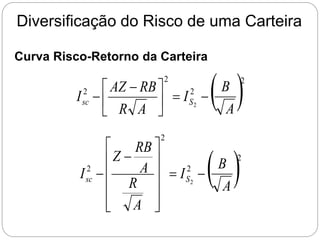
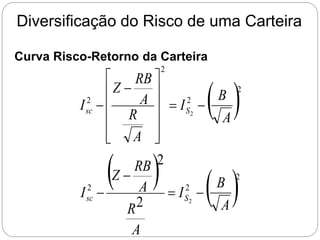
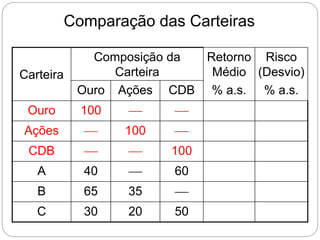
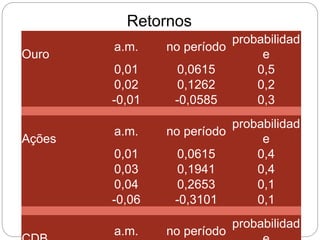
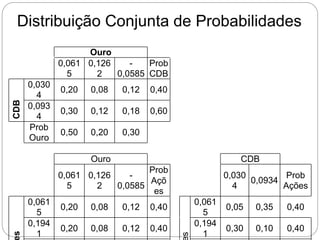
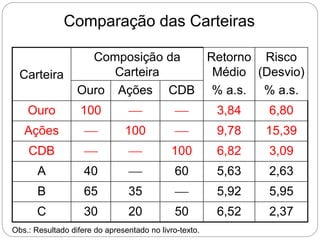
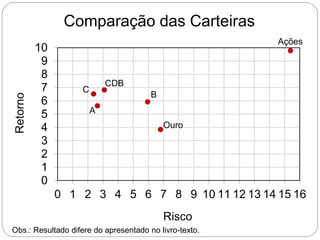
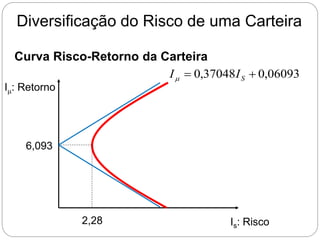
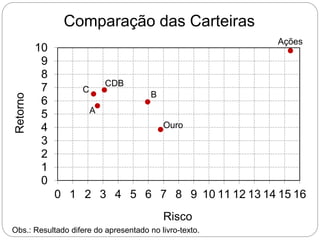
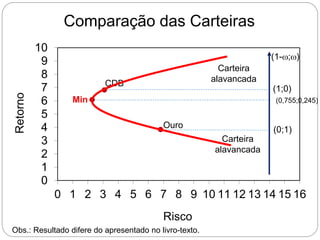
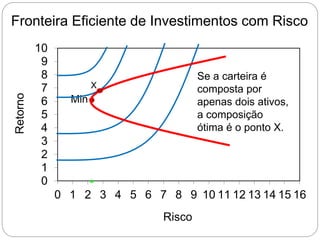
O documento descreve como calcular o retorno e o risco de uma carteira de investimentos composta por dois ativos. Mostra que a composição de risco mínimo ocorre quando os ativos são ponderados de acordo com a razão entre seus desvios padrões. Apresenta também a curva de riscos e retornos da carteira, que relaciona o retorno médio com o desvio padrão e geralmente tem formato de hipérbole.

1. Decisões em Condições de Risco
Os Modelos de Markowitz e Sharpe,
o CAPM
Parte 1
ADM4007 Finanças Corporativas
Baseado em SECURATO, J. R. Decisões financeiras em condições de
risco. São Paulo: Atlas, 1996.

2. Diversificação do Risco de uma Carteira
Considere uma carteira de investimentos
composta dos ativos A1 e A2, respectivamente
nas proporções w e (1 - w)
As taxas de retorno desses ativos são,
respectivamente, I1 e I2, com distribuições de
probabilidade conhecidas:
Problema: determinar a taxa de retorno da
carteira (Ic):
   
2
2
1
1
,
:
,
: 2
1 S
S I
I
D
I
e
I
I
D
I 

  2
1 1 I
I
IC w
w 



3. Diversificação do Risco de uma Carteira
Cálculo do retorno médio da carteira
   
 
2
1 1 I
I
E
I
E
I C
C w
w
 



     
2
1 1 I
E
I
E
I C w
w
 


ou
  2
1 1 

 w
w I
I
I C 



4. Diversificação do Risco de uma Carteira
Cálculo do desvio do retorno da carteira
   
 
2
1
2
1 I
I
S
I
S
I C
SC w
w 




5. Diversificação do Risco de uma Carteira
Cálculo do desvio do retorno da carteira
Se I1 e I2 são independentes (em geral não são!),
então cov(I1,I2)=0
     
2
1
2
2
2
2
,
cov
1
2
1 2
1
I
I
I
I
I S
S
SC w
w
w
w 




Se I1 e I2 são dependentes, deve-se calcular a
cov(I1,I2), que dependerá do cálculo das
probabilidades conjuntas P(I1,I2).

6. Diversificação do Risco de uma Carteira
Composição da carteira de risco mínimo
Risco:
     
2
1
2
2
2
2
,
cov
1
2
1 2
1
I
I
I
I
I S
S
SC w
w
w
w 




Condição de risco mínimo:
0



w
SC
I

7. Diversificação do Risco de uma Carteira
Composição da carteira de risco mínimo
Risco:
     
2
1
2
2
2
2
,
cov
1
2
1 2
1
I
I
I
I
I S
S
SC w
w
w
w 




     
2
1
2
2
S
2
2
S
2
SC I
,
I
cov
2ω
2ω
I
ω
2ω
1
I
ω
I 2
1






 
   
  2
2
1
2
2
2
1
2
2
2
2
2
1
2
2
2 S
S
S
S
SC I
I
,
I
cov
I
I
,
I
cov
I
I
I 




 w
w
   
2
1
2
2
1
2
S
2
2
S
2
S
2
S
2
SC I
,
I
cov
2ω
I
,
I
cov
2ω
I
ω
I
2ω
I
I
ω
I 2
2
2
1







8. Risco:
A
 
   
  2
2
1
2
2
2
1
2
2
2
2
2
1
2
2
2 S
S
S
S
SC I
I
,
I
cov
I
I
,
I
cov
I
I
I 




 w
w
2B
Diversificação do Risco de uma Carteira
Composição da carteira de risco mínimo
2
2
2
2 S
SC I
B
A
I 

 w
w

9. Diversificação do Risco de uma Carteira
Composição da carteira de risco mínimo
Risco: 2
2
2
2 S
SC I
B
A
I 

 w
w
Condição de risco mínimo:
0



w
SC
I

10. Diversificação do Risco de uma Carteira
Composição da carteira de risco mínimo
Risco: 2
2
2
2 S
SC I
B
A
I 

 w
w
Condição de risco mínimo:
0
2
2
2
2
2
2
2







S
SC
I
B
A
B
A
I
w
w
w
w
0
2
2 
 B
Aw  B
A 2
2 
w 
A
B

w

11. Diversificação do Risco de uma Carteira
Composição da carteira de risco mínimo
Risco: 2
2
2
2 S
SC I
B
A
I 

 w
w
Condição de risco mínimo:
A
B

w
Então 2
2
2
2
min
2 S
SC I
A
B
B
A
B
A
I 




ou
A
B
I
I S
SC
2
2
2
min



12. Diversificação do Risco de uma Carteira
Curva Risco-Retorno da Carteira
Como:   2
1 1 

 w
w I
I
I C 


Então:   2
2
1 


 w I
I
I
I C 


2
1
2




w
I
I
I
I C




Lembrando que 2
2
2
2 S
SC I
B
A
I 

 w
w
2
2
1
2
2
2
1
2
2
2 S
C
C
SC I
I
I
I
I
B
I
I
I
I
A
I 































13. Diversificação do Risco de uma Carteira
Curva Risco-Retorno da Carteira
2
2
1
2
2
2
1
2
2
2 S
C
C
SC I
I
I
I
I
B
I
I
I
I
A
I 






























2

 I
I
Z C 

Então:
Seja: 2
1 
 I
I
R 

0
2 2
2
2
2
2



 S
sc I
Z
R
B
Z
R
A
I

14. Diversificação do Risco de uma Carteira
Curva Risco-Retorno da Carteira
• Esta equação pode representar uma elipse,
uma hipérbole ou uma parábola.
• Em geral, a curva representativa do retorno
médio de uma carteira em função do risco
será uma hipérbole.
0
2 2
2
2
2
2



 S
sc I
Z
R
B
Z
R
A
I
Ver pag.139-143

15. Diversificação do Risco de uma Carteira
Curva Risco-Retorno da Carteira
0
2 2
2
2
2
2



 S
sc I
Z
R
B
Z
R
A
I
  0
2 2
2
2
2











 S
sc I
A
B
R
Z
A
R
Z
A
I
      0
2 2
2
2
2
2
2













 S
sc I
A
B
A
B
A
B
R
Z
A
R
Z
A
I

16. Diversificação do Risco de uma Carteira
Curva Risco-Retorno da Carteira
      0
2 2
2
2
2
2
2













 S
sc I
A
B
A
B
A
B
R
Z
A
R
Z
A
I
  0
2
2
2
2
2
















 S
sc I
A
B
A
B
R
Z
A
I
 
A
B
I
A
R
RB
AZ
I S
sc
2
2
2
2
2







 


17. Diversificação do Risco de uma Carteira
Curva Risco-Retorno da Carteira
 
A
B
I
A
R
RB
AZ
I S
sc
2
2
2
2
2







 

 
A
B
I
A
R
A
RB
Z
I S
sc
2
2
2
2
2

















18. Diversificação do Risco de uma Carteira
Curva Risco-Retorno da Carteira
 
A
B
I
A
R
A
RB
Z
I S
sc
2
2
2
2
2
















   
A
B
I
A
R
A
RB
Z
I S
sc
2
2
2
2
2
2





19. Diversificação do Risco de uma Carteira
Curva Risco-Retorno da Carteira
   
A
B
I
A
R
A
RB
Z
I S
sc
2
2
2
2
2
2




  1
0
2
2
2
2
2
2
2
2
2
2







































A
B
I
A
R
A
RB
I
I
A
B
I
I
S
C
S
sc


2

 I
I
Z C 


20. Diversificação do Risco de uma Carteira
Curva Risco-Retorno da Carteira
  1
0
2
2
2
2
2
2
2
2
2
2







































A
B
I
A
R
A
RB
I
I
A
B
I
I
S
C
S
sc


Equação reduzida da hipérbole de centro:
  







A
RB
I
I
I centro
C
sc 2
;
0
; 


21. Diversificação do Risco de uma Carteira
Curva Risco-Retorno da Carteira
  1
0
2
2
2
2
2
2
2
2
2
2







































A
B
I
A
R
A
RB
I
I
A
B
I
I
S
C
S
sc


Equação reduzida da hipérbole com assíntotas:










A
RB
I
I
A
R
I SC
C 2



22. Diversificação do Risco de uma Carteira
Curva Risco-Retorno da Carteira









A
RB
I
I
A
R
I SC
C 2


Ic: Retorno
A
RB
I 
2

ISC mínimo Isc: Risco

23. Resumindo
Média







n
j
j
j
n
n
c I
I
I
I
I
1
2
2
1
1 



 w
w
w
w 
Desvio (Risco)
 

 



n
k
j
k
j
k
j
n
j
Sj
j
SC I
I
I
I ,
cov
2
1
2
2
2
w
w
w

24. Exercício
• Considere três investidores (A, B e C) que
estudam a possibilidade de aplicar em ouro,
ações ou CDB pelo prazo de 180 dias.
• Calcule:
a) Média e desvios (riscos) dos ativos
b) Risco de cada carteira

25. Comparação das Carteiras
Carteira
Composição da
Carteira
Retorno
Médio
Risco
(Desvio)
Ouro Ações CDB % a.s. % a.s.
Ouro 100  
Ações  100 
CDB   100
A 40  60
B 65 35 
C 30 20 50

26. Retornos
Ouro
a.m. no período
probabilidad
e
0,01 0,0615 0,5
0,02 0,1262 0,2
-0,01 -0,0585 0,3
Ações
a.m. no período
probabilidad
e
0,01 0,0615 0,4
0,03 0,1941 0,4
0,04 0,2653 0,1
-0,06 -0,3101 0,1
a.m. no período
probabilidad

27. Distribuição Conjunta de Probabilidades
Ouro
0,061
5
0,126
2
-
0,0585
Prob
CDB
CDB
0,030
4
0,20 0,08 0,12 0,40
0,093
4
0,30 0,12 0,18 0,60
Prob
Ouro
0,50 0,20 0,30
Ouro CDB
0,061
5
0,126
2
-
0,0585
Prob
Açõ
es
0,030
4
0,0934
Prob
Ações
s
0,061
5
0,20 0,08 0,12 0,40
s
0,061
5
0,05 0,35 0,40
0,194
1
0,20 0,08 0,12 0,40
0,194
1
0,30 0,10 0,40

28. Comparação das Carteiras
Carteira
Composição da
Carteira
Retorno
Médio
Risco
(Desvio)
Ouro Ações CDB % a.s. % a.s.
Ouro 100   3,84 6,80
Ações  100  9,78 15,39
CDB   100 6,82 3,09
A 40  60 5,63 2,63
B 65 35  5,92 5,95
C 30 20 50 6,52 2,37
Obs.: Resultado difere do apresentado no livro-texto.

29. Comparação das Carteiras
0
1
2
3
4
5
6
7
8
9
10
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Retorno
Risco
Ações
Ouro
CDB
A
B
C
Obs.: Resultado difere do apresentado no livro-texto.

30. Exercício
Lembrando que:
Composição da carteira de risco mínimo
Risco:
Condição de risco mínimo:
0
2
2
2
2
2
2
2







S
SC
I
B
A
B
A
I
w
w
w
w
0
2
2 
 B
Aw  B
A 2
2 
w 
A
B

w
A
 
   
  2
2
1
2
2
2
1
2
2
2
2
2
1
,
cov
2
2
,
cov
2 S
S
S
S
SC I
I
I
I
I
I
I
I
I 




 w
w
2B

31. Exercício
Calcule:
• a composição da carteira com ouro e CDB
que dá o ponto de risco mínimo;
• O retorno médio dessa carteira de risco
mínimo.

32. Diversificação do Risco de uma Carteira
Curva Risco-Retorno da Carteira
06093
,
0
37048
,
0 
 S
I
I
I: Retorno
2,28 Is: Risco
6,093

33. Comparação das Carteiras
0
1
2
3
4
5
6
7
8
9
10
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Retorno
Risco
Ações
Ouro
CDB
A
B
C
Obs.: Resultado difere do apresentado no livro-texto.

34. Comparação das Carteiras
0
1
2
3
4
5
6
7
8
9
10
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Retorno
Risco
Ações
Ouro
CDB
A
B
C
Obs.: Resultado difere do apresentado no livro-texto.
Min

35. Comparação das Carteiras
0
1
2
3
4
5
6
7
8
9
10
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Retorno
Risco
Ouro
CDB
Obs.: Resultado difere do apresentado no livro-texto.
Min
(1-w;w)
(1;0)
(0;1)
(0,755;0,245)
Carteira
alavancada
Carteira
alavancada

36. Fronteira Eficiente de Investimentos com Risco
0
1
2
3
4
5
6
7
8
9
10
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Retorno
Risco
Min
X
Se a carteira é
composta por
apenas dois ativos,
a composição
ótima é o ponto X.

37. Fronteira Eficiente de Investimentos com Risco
Retorno
Risco
Considerando o caso
de uma carteira
formada por n ativos,
é possível obter
hipérboles
representando a
relação risco-retorno
entre um ativo Aj e
uma composição
relativa dos n-1 ativos
remanescentes.

38. Fronteira Eficiente de Investimentos com Risco
Retorno
Risco
Fronteira eficiente de investimentos de um portfólio
(carteira) é o conjunto de todas carteiras que:
a) Dado um nível de risco, não existe carteira com maior retorno; e,
b) Dado um nível de retorno, não existe carteira com menor risco.
A curva denominada
fronteira eficiente de
investimentos com
riscos é a envoltória
da família de
hipérboles da
carteira.