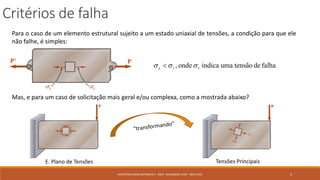
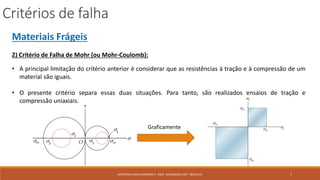
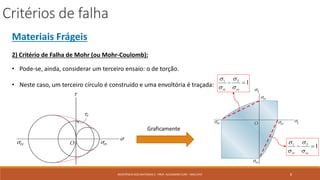
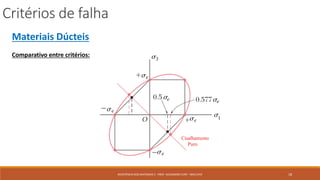
O documento discute critérios para prever falha em materiais sob tensões. Ele apresenta quatro critérios principais: 1) Critério da máxima tensão normal para materiais frágeis, 2) Critério de Mohr para materiais frágeis, 3) Critério de Tresca para materiais dúcteis baseado na máxima tensão de cisalhamento, e 4) Critério de von Mises para materiais dúcteis baseado na máxima energia de distorção. O documento também discute como esses critérios podem ser aplic