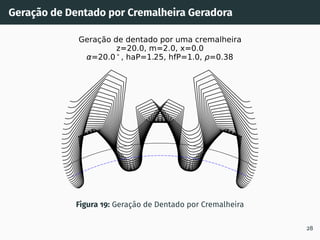
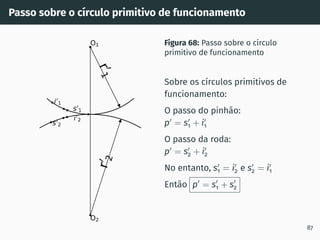
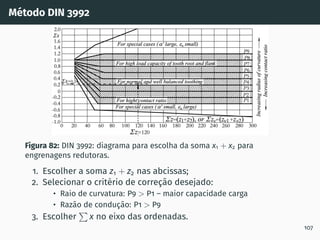
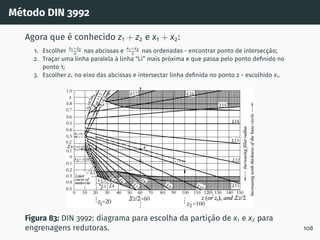
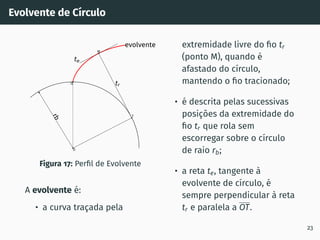
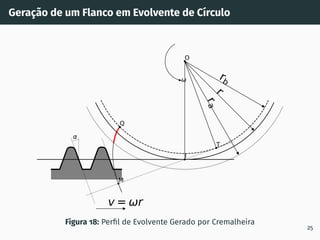
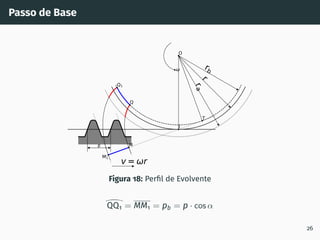
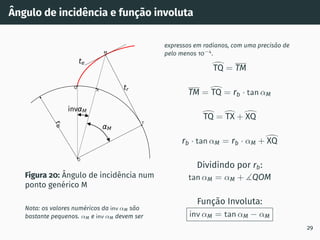
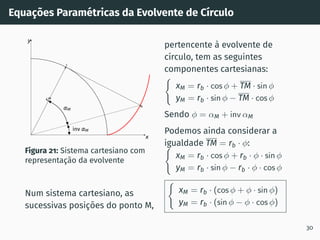
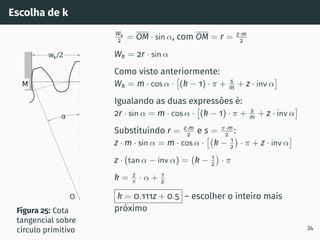
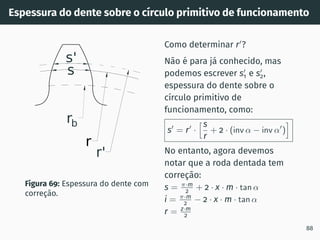
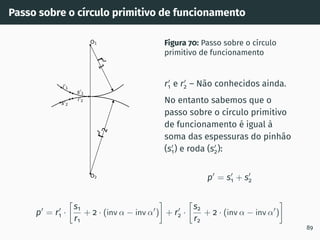
1. O documento apresenta os conceitos fundamentais de engrenagens, incluindo a classificação, perfis de dentado e conceitos como círculo primitivo, passo e módulo. 2. São descritos os processos de geração de dentado por cremalheira, incluindo a evolvente de círculo e o ângulo de incidência. 3. São apresentadas normas e referências técnicas relevantes para o projeto e análise de engrenagens.

1. Engrenagens
Órgãos de Máquinas
Carlos Fernandes
2022/2023
Licenciatura em Engenharia Mecânica

2. Nota introdutória
A generalidade dos diagramas apresentados, foram largamente
influenciados pelo trabalho do Professor Paulo Tavares de Castro.
Os script Python utilizados para geração das figuras e animações do
presente documento, serão disponibilizados aos estudantes que
demonstrem interesse em utilizar tais ferramentas.
Software recomendado:
• GEARpie: software Python de cálculo de engrenagens,
disponı́vel em https://github.com/cfernandesFEUP/GEARpie
• KISSSoft: software comercial para cálculo de órgãos de
máquinas (ver instruções de instalação nos diapositivos das
aulas laboratoriais)
1

3. Bibliografia Engrenagens
Principal:
• Henriot, Georges; Traité théorique et pratique des engrenages;
Dunod
• MAAG Gear Company, Ltd.; MAAG gear book
Complementar:
• Branco, C. M., Ferreira, J. M., Costa, J. D., Ribeiro, A. S.; Projecto de
Órgãos de Máquinas, Fundação Calouste Gulbenkian
Sugestão de leitura:
• Vullo, V.; Gears (3 volumes), Springer International Publishing.
2

4. Normas Engrenagens
Disponı́veis nos conteúdos:
• NF E 23-001: Vocabulaire des Engrenages: Definitions
Géométriques
• NF E 23-002: Vocabulaire des Engrenages: Definitions
Géométriques Engrenages à vis
• NF E 23-011: Engrenages: Crémaillére de Référence et Modules
des Rous Cylindriques à Developpante de Mécnique Générale et
de Grosse Méchanique
• NF E 23-012: Engrenages Cylindriques: Indications à Fournir au
Fabricant d’Engrenages
• NF E 23-013: Engrenages: Déport de Dentures des Roues
Cylindriques pour Engrenages Réducteurs
3

5. Normas Engrenagens
• DIN 780: Series of modules for gears
• DIN 867: Basic rack of Cylindrical Gears with Involute Teeth for
General and Heavy Engineering
• DIN 868: General Definitions and Specification Factors for
Gears, Gear Pairs and Gear Trains
• DIN 3960: Concepts and parameters associated with cylindrical
gears and cylindrical gear pairs with involute teeth
• DIN 3972: Reference Profiles of Gear-cutting Tools for Involute
Tooth Systems according to DIN 867
• DIN 3975: Terms and Definitions for Cylindrical Worm Gears with
Shaft Angle 90°
4

6. Normas Engrenagens
• DIN 3978: Helix Angles for Cylindrical Gear Teeth
• DIN 3979: Tooth Damage on Gear Trains: Designation,
Characteristics, Causes
• DIN 3998: Denominations on gears and gear pairs
• NP EN ISO 2203: Desenhos técnicos - Representação
convencional de engrenagens
Não disponı́veis nos conteúdos, mas relevantes:
• ISO 6336: Calculation of load capacity of spur and helical gears
5

7. Hiperligação para aula
Aula 1
Aula 2
Aula 3
Aula 4
Aula 5
Aula 6
Aula 7
Aula 8
Aula 9
Aula 10
Aula 11
Referências
6

8. Aula 1

9. Sumário
1. Engrenagens: Introdução e Classificação 8
2. Perfis de Dentado 12
3. Rodas de atrito 16
4. Conceitos básicos: cı́rculo primitivo, passo e módulo 17
5. Cremalheira geradora 19
6. Razão de multiplicação e transmissão 21
7

10. Introdução
Engrenagem:
Conjunto de duas rodas dentadas acopladas entre si.
• Serve para a transmissão do
movimento de rotação entre
veios.
• Um elemento isolado de uma
engrenagem é chamado de
roda dentada.
• Ao elemento de maior número
de dentes chama-se roda e ao
elemento de menor número de
dentes chama-se pinhão.
• A representação convencional
de engrenagens em desenho
técnico é feita de acordo com a
NP EN ISO 2203.
roda
pinhão
Figura 1: Engrenagem
8

11. Classificação das Engrenagens
(a) Paralelos (b) Esquerda (c) Esquerda
(d) Concorrentes (e) Esquerda
Figura 2: Classificação quanto à Posição dos Eixos [1].
9

12. Classificação das Engrenagens
(a) Recto (b) Helicoidal
Figura 3: Classificação quanto ao Tipo de Dentado [1].
10

13. Classificação das Engrenagens
(a) Interior (b) Exterior
Figura 4: Classificação quanto à Posição do Centro Instantâneo de Rotação
[1].
11

14. Perfis de Dentado
Perfil em Cicloide
Aplicações:
• Relógios
• Moinhos de fabrico de papel
• Moinhos de açúcar
Figura 5: Engrenagem com perfil em
cicloide
12

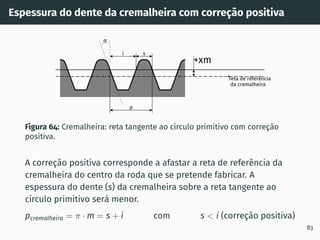
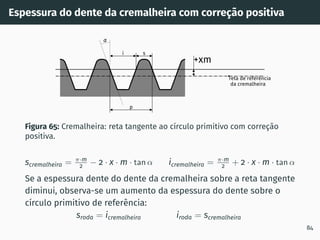
15. Perfis de Dentado
Perfil em arco circular
• Caixas de velocidades de
muito baixa rotação
Figura 6: Engrenagem com perfil em
arco circular (Wildhaber-Novikov) [2]
Perfil S
• Apresentam algumas
vantagens em engrenagens
poliméricas
Figura 7: Engrenagem com perfil S [3] 13

16. Perfis de Dentado
O Perfil em Evolvente de Cı́rculo é o mais comum em engrenagens,
pois apresenta as seguintes vantagens:
• Fabrico relativamente simples;
• Não é sensı́vel à variação de entre-eixo mantendo a relação de
transmissão constante;
• O ângulo de pressão é constante ao longo do engrenamento
garantindo um funcionamento suave.
Figura 8: Engrenagem de dentado reto com perfil em evolvente de cı́rculo
14

17. Aplicações das Engrenagens em Perfil de Evolvente
(a) (b) (c)
(d) (e)
Figura 9: Exemplos de utilização de engrenagens.
(a) Caixa de velocidades de um Porsche 971 Panamera; (b) Motor MAN DF 3876 LF; (c) Impressora Xerox ColorQube 8570; (d) Relógio da
Igreja da Santa Cruz, Dülmen, Renânia do Norte-Vestfália, Alemanha; (e) Caixa de Engrenagens com Parafuso sem-fim/roda de coroa
15

18. Rodas de Atrito
1
2
I
O1
O2
r2
r1
Figura 10: Rodas de Atrito
Entre-eixo:
O1O2 = a
(
a = r1 + r2
ω1 · r1 = ω2 · r2
• r1 e r2 são designados por
raios primitivos
• O ponto I tem a designação
de ponto primitivo
16

19. Conceitos básicos: cı́rculo primitivo, passo e módulo
Figura 11: Dentado Normal
r raio primitivo
ra raio de cabeça (ou addendum)
rd raio de pé (ou deddendum)
rb raio de base
m módulo (normalizado)
α ângulo de pressão
p passo
O perı́metro do cı́rculo primitivo
é 2 · π · r, então:
2 · π · r = z · p
O raio primitivo de referência (r)
é função do módulo e do
número de dentes da roda
dentada (z):
r =
z · p
2π
=
z · m
2
Outras relações relevantes:
rd = r − hf = r − 1.25 · m
ra = r + ha = r + m
rb = r · cos α 17

20. Cremalheira geradora - Processo MAAG
rb
r
r
a
reta de referência
da cremalheira
p
v= r
O
T
I
Figura 12: Processo MAAG para geração de dentado.
r = z·m
2 ra = r + m rb = r · cos α p = π · m
18

21. Cremalheira geradora
Figura 13: Cremalheira de módulo m=1.
Perfil de referência do Tipo A, de
acordo com a ISO 53/ DIN 867:
ha = 1.25m altura de cabeça
hf = m altura de pé
rF = 0.38m raio de curvatura
De notar que são utilizados
outros perfis de referência.
Os valores do módulo m (mm)
são normalizados segundo a DIN
780.
Série I (preferencial):
0.05 0.06 0.08 0.1 0.12 0.16 0.2
0.25 0.3 0.4 0.5 0.6 0.7 0.8
0.9 1 1.25 1.5 2 2.5 3
4 5 6 8 10 12 16
20 25 32 40 50 60
19

22. Razão de multiplicação
z2
z1
Figura 14: Engrenagem
Razão de multiplicação u
representa a razão entre o
número de dentes da roda z2 e o
número de dentes do pinhão z1:
u =
z2
z1
A razão de multiplicação é
sempre |u| ≥ 1
20

23. Razão de transmissão
Razão de transmissão i, representa a razão das velocidades
angulares das rodas dentadas mandante (subscrito a) e mandada
(subscrito b):
i =
ωa
ωb
=
na
nb
= −
zb
za
A engrenagem é redutora para |i| > 1.
z2
ωb
z1
ωa
Figura 15: Redutora
A engrenagem é multiplicadora para |i| < 1.
z2
ωa
z1
ωb
Figura 16: Multiplicadora
21

24. Aula 2

25. Sumário
1. Cı́rculo de base e evolvente desse cı́rculo 23
2. Geração de um flanco em evolvente de cı́rculo 25
3. Conceito de ângulo de incidência e função involuta 29
4. Espessura do dente 31
5. Cota tangencial em K dentes 33
22

26. Evolvente de Cı́rculo
r
b
tr
O
Q
M
T
te
evolvente
Figura 17: Perfil de Evolvente
A evolvente é:
• a curva traçada pela
extremidade livre do fio tr
(ponto M), quando é
afastado do cı́rculo,
mantendo o fio tracionado;
• é descrita pelas sucessivas
posições da extremidade do
fio tr que rola sem
escorregar sobre o cı́rculo
de raio rb;
• a reta te, tangente à
evolvente de cı́rculo, é
sempre perpendicular à reta
tr e paralela a OT.
23

27. Geração da Evolvente de Cı́rculo
24
0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4
Ângulo / rad
101
100
0
100
101 Declive de te
Declive tr
mtr
mte

28. Geração de um Flanco em Evolvente de Cı́rculo
rb
r
r
a
v= r
O
T
I
Q
M
Figura 18: Perfil de Evolvente Gerado por Cremalheira
25

29. Geração de um Flanco em Evolvente de Cı́rculo
25
O
T
I

30. Passo de Base
rb
r
r
a
p
v= r
O
T
I
Q
Q1
M
M1
Figura 18: Perfil de Evolvente
>
QQ1 = MM1 = pb = p · cos α
26

31. Geração de Dentado por Cremalheira
27
Primitivo (x=0)
Primitvo
Círculo de Base
Roda dentada:
z=20.0
m=2.0
x=0.0
Cremalheira:
=20
ha=1.25
hf=1.0
=0.38

32. Geração de Dentado por Cremalheira Geradora
Geração de dentado por uma cremalheira
z=20.0, m=2.0, x=0.0
=20.0 , haP=1.25, hfP=1.0, =0.38
Figura 19: Geração de Dentado por Cremalheira
28

33. Ângulo de incidência e função involuta
r
b
tr
O
Q
M
T
te
X
inv M
M
Figura 20: Ângulo de incidência num
ponto genérico M
Nota: os valores numéricos da inv αM são
bastante pequenos. αM e inv αM devem ser
expressos em radianos, com uma precisão de
pelo menos 10−4
.
>
TQ = TM
TM =
>
TQ = rb · tan αM
>
TQ =
>
TX +
>
XQ
rb · tan αM = rb · αM +
>
XQ
Dividindo por rb:
tan αM = αM + ∡QOM
Função Involuta:
inv αM = tan αM − αM
29

34. Equações Paramétricas da Evolvente de Cı́rculo
r
b
x
y
M
T
inv M
M
Figura 21: Sistema cartesiano com
representação da evolvente
Num sistema cartesiano, as
sucessivas posições do ponto M,
pertencente à evolvente de
cı́rculo, tem as seguintes
componentes cartesianas:
(
xM = rb · cos ϕ + TM · sin ϕ
yM = rb · sin ϕ − TM · cos ϕ
Sendo ϕ = αM + inv αM
Podemos ainda considerar a
igualdade TM = rb · ϕ:
(
xM = rb · cos ϕ + rb · ϕ · sin ϕ
yM = rb · sin ϕ − rb · ϕ · cos ϕ
(
xM = rb · (cos ϕ + ϕ · sin ϕ)
yM = rb · (sin ϕ − ϕ · cos ϕ)
30

35. Espessura do Dente
ra
r
rb
invαM
invα
Q'
Y'
M'
M
Y
Q
Figura 22: Espessura do dente num
ponto genérico M
Relembrar:
r = z·m
2
rb = r · cos α
ra = r + m
Para dentado normal (sem
correção), a espessura do dente
sobre o cı́rculo primitivo (r) é:
s =
>
YY’ = p
2 = π·m
2
Num outro ponto M, a espessura
é:
sM = rM · ∡MOM′
= rM · s
r − 2 · ∡YOM
= rM ·
s
r − 2 · (∡QOM − ∡QOY)
= rM ·
s
r − 2 · (inv αM − inv α)
sM = rM ·
hs
r
+ 2 · (inv α − inv αM)
i
31

36. Espessura do dente sobre o cı́rculo de base
r
rb
invα
Q'
Y'
Y
Q
Figura 23: Espessura da base do
dente
A espessura do dente para um
ponto genérico M com ângulo de
incidência αM é:
sM = rM ·
hs
r
+ 2 · (inv α − inv αM)
i
Sobre o cı́rculo de base, o
ângulo de incidência αM é nulo.
Assim, temos um caso particular
da espessura do dente sobre o
cı́rculo de base ser:
sb = rb ·
s
r
+ 2 inv α
Relembrar que:
• α é o ângulo de pressão,
normalmente 20◦
.
• inv α = tan α − α
32

37. Cota tangencial sobre k dentes
ra
Wk
M'
M
Q'
Q
rb
T
Figura 24: Cota tangencial sobre k=3
dentes
A cota tangencial sobre 3 dentes:
W3 = MM′ =
QQ’
W3 = 2 pb
|{z}
passo
de
base
+ sb
|{z}
espessura
da
base do dente
Para qualquer k:
Wk =
QQ’ = (k − 1) · pb + sb
Passo de base:
2π · rb = z · pb
rb = r · cos α
pb = 2π·r
z · cos α = p · cos α
A espessura do dente sobre o circulo de base:
sb = rb · s
r + 2 inv α
Wk = m · cos α ·
h
(k − 1) · π +
s
m
+ z · inv α
i
33

38. Escolha de k
M
T
wk/2
α
O
Figura 25: Cota
tangencial sobre
cı́rculo primitivo
Wk
2 = OM · sin α, com OM = r = z·m
2
Wk = 2r · sin α
Como visto anteriormente:
Wk = m · cos α ·
(k − 1) · π + s
m + z · inv α
Igualando as duas expressões é:
2r · sin α = m · cos α ·
(k − 1) · π + s
m + z · inv α
Substituindo r = z·m
2 e s = π·m
2 :
z · m · sin α = m · cos α ·
k − 1
2
· π + z · inv α
z · (tan α − inv α) = k − 1
2
· π
k = z
π · α + 1
2
k = 0.111z + 0.5 – escolher o inteiro mais
próximo
34

39. Aula 3

40. Sumário
1. Engrenamento 36
2. Caminho de Engrenamento 38
3. Razão de Condução 40
4. Valor Crı́tico da Razão de Condução 42
5. Entre-eixo de corte e de funcionamento 45
35

41. Engrenamento
O1
Q1
X
T1
t1
(a)
O2
Q2
Y
T2
t2
(b)
Figura 26: Perfis em evolvente.
O2
Q2
Y T2
t2
O1
Q1
X
T1
t1
Figura 27: Contacto das evolventes
sobre a reta de engrenamento
• Mover a Figura 26a de
maneira a fazer coincidir t1
com t2 da Figura 26b;
• Fazer o Ponto X da Figura
26a coincidir com o Ponto Y
da Figura 26b. 36

42. Engrenamento
1
2
r
b
1
r
b
2
T1
T2
O1
O2
I
M
Q1
Q2
Figura 28: Contacto das evolventes
sobre a reta de engrenamento T1T2
As evolvente aos cı́rculos de
base do pinhão (com centro em
O1) e da roda (com centro em
O2) são:
• tangentes sobre a reta de
engrenamento no ponto M;
• as evolventes crescem
desde Q1 e Q2,
respectivamente.
Entre-eixo normal ou de corte:
O1O2 = a = r1 + r2 = m ·
z1 + z2
2
Raio de base: rb = r · cos α 37

43. Inı́cio do Caminho de Engrenamento
1
2
T1
T2
O1
O2
I
Figura 29: Inı́cio do Caminho de
Engrenamento
O inı́cio do engrenamento
acontece quando:
• O raio de cabeça (ra1) da
roda dentada 1 contacta
com o flanco da roda
dentada mandante 2;
• o contacto entre os flancos
acontece sempre sobre a
linha T1T2;
• Este ponto designa-se por A.
38

44. Inı́cio do Caminho de Engrenamento
1
2
T1
T2
O1
O2
I
A
Figura 29: Inı́cio do Caminho de
Engrenamento
O inı́cio do engrenamento
acontece quando:
• O raio de cabeça (ra1) da
roda dentada 1 contacta
com o flanco da roda
dentada mandante 2;
• o contacto entre os flancos
acontece sempre sobre a
linha T1T2;
• Este ponto designa-se por A.
38

45. Fim do Caminho de Engrenamento
1
2
T1
T2
O1
O2
I
B
Figura 30: Fim do Caminho de
Engrenamento
O fim do engrenamento
acontece quando:
• O raio de cabeça (ra2) da
roda dentada 2 deixa de
contactar com o flanco da
roda dentada mandada 1;
• o contacto entre os flancos
acontece sempre sobre a
linha T1T2;
• Este ponto designa-se por B.
39

46. Fim do Caminho de Engrenamento
1
2
T1
T2
O1
O2
I
Figura 30: Fim do Caminho de
Engrenamento
O fim do engrenamento
acontece quando:
• O raio de cabeça (ra2) da
roda dentada 2 deixa de
contactar com o flanco da
roda dentada mandada 1;
• o contacto entre os flancos
acontece sempre sobre a
linha T1T2;
• Este ponto designa-se por B.
39

47. Razão de Condução
1
2
T1
T2
O1
O2
I
r
a
1
r
a
2
A
B
Figura 31: Descrição do caminho de
engrenamento
T1T2 é designada por recta de
engrenamento (inglês: “line of
action”).
AB é designado por segmento de
engrenamento ou caminho de
engrenamento (inglês: “path of
contact”).
O1I = r1 = z1·m
2
O2I = r2 = z2·m
2
ra1 = r1 + m
ra2 = r2 + m 40

48. Razão de Condução
pb
pb
1
2
T1
T2
O1
O2
I
A
B
Figura 32: Razão de Condução
ϵα =
AB
pb
AB = AI + IB
AI = T1A − T1I IB = T2B − T2I
ϵα =
p
r2
a1 − r2
b1 +
p
r2
a2 − r2
b2 − a sin α
pb
41

49. Valor Crı́tico da Razão de Condução
1
2
T1
T2
O1
O2
I
A
Figura 33: Razão de Condução
ϵα =
AB
pb
O valor da razão de condução ϵα
deve ser sempre 1.
Quando AB pb, ou seja ϵα 1:
• Um par de dentes entra em
contacto no ponto A;
• percorre todo o caminho de
engrenamento até B sem
que o par seguinte engrene.
Nesta situação haverá um
perı́odo de descontinuidade na
transmissão do movimento, que
quando reiniciado causará
choque entre os flancos dos
dentes. 42

50. Valor Crı́tico da Razão de Condução
pb
pb
1
2
T1
T2
O1
O2
I
A
B
Figura 33: Razão de Condução
ϵα =
AB
pb
O valor da razão de condução ϵα
deve ser sempre 1.
Quando AB pb, ou seja ϵα 1:
• Um par de dentes entra em
contacto no ponto A;
• percorre todo o caminho de
engrenamento até B sem
que o par seguinte engrene.
Nesta situação haverá um
perı́odo de descontinuidade na
transmissão do movimento, que
quando reiniciado causará
choque entre os flancos dos
dentes. 42

51. Formas de Variar a Razão de Condução
pb
pb
1
2
T1
T2
O1
O2
I
A
B
Figura 34: Razão de Condução
O valor da razão de condução ϵα
aumenta quando:
• a altura de cabeça dos
dentes (ha) aumenta;
• o raio primitivo de uma das
rodas aumenta.
O valor da razão de condução ϵα
diminui quando:
• o ângulo de pressão (α)
aumenta.
O aumento da razão de condução é
geralmente benéfico pois reduz a
carga média que atua sobre os
dentes. 43

52. Entre-eixo de corte e de funcionamento
T1
T2
O1
O2
I
ra1
ra2
A
B
Figura 35: Entre-eixo de corte
0
0
0
T1
T2
O1
O2
I
ra1
ra2
A
B
Figura 36: Entre-eixo de
funcionamento
a = r1 + r2 = m · z1+z2
2 a′
a
44

53. Entre-eixo de corte e de funcionamento
0
0
0
T1
T2
O1
O2
I
ra1
ra2
A
B
Figura 37: Entre-eixo de
funcionamento
a′
a
No caso da imposição do entre-eixo
a′
a, o ângulo de pressão de
funcionamento α′
é maior que o
ângulo de pressão de corte α.
a′
· cos α′
= a · cos α
Igualdade de velocidades no
primitivo:
ω1 · r′
1 = ω2 · r′
2
(
a′
= r′
1 + r′
2
ω2
ω1
= z1
z2
=
r′
1
r′
2
45

54. Aula 4

55. Sumário
1. Raio ativo de pé 47
2. Velocidades no ponto primitivo 48
3. O escorregamento no engrenamento 49
4. Escorregamento especı́fico 58
46

56. Raio ativo de pé
r
A
1
2
T1
T2
O1
O2
I
A
Figura 38: Raio ativo de pé rA.
rA
2
= rb2
2
+ T2A
2
T2A = T2T1 − T1A =
(r1 + r2) · sin α −
p
ra1
2 − rb1
2
Situação aplicável às situações:
1. Raio ativo de pé rA de
funcionamento: engrenamento
do pinhão z1 com a roda z2;
2. Raio ativo de pé rA de corte:
corte da roda z2 pelo
buril-pinhão z1 – abaixo de rA o
perfil não é em evolvente de
cı́rculo.
· O valor mı́nimo de rA é obtido pela geração por cremalheira.
· rA de corte terá de ser sempre menor que rA de funcionamento. 47

57. Velocidades no Ponto Primitivo
vI1 =vI2
vb1=vb2
v
r
1
=
v
r
2
1
2
T1
T2
O1
O2
I
Figura 39: Velocidades no Ponto
Primitivo
As velocidades sobre o ponto
primitivo (I) são iguais para o
pinhão e roda da engrenagem.
A componente na direcção do
caminho de engrenamento
(tangencial ao cı́rculo de base)
vb1 = vb2 em qualquer ponto de
contacto compreendido entre
T1T2:
• condição necessária para
garantir continuidade da
transmissão de movimento
da roda mandante para a
roda mandada;
48

58. O escorregamento no engrenamento
T1
T2
I
p1
p2
A
B
Figura 40: Escorregamento no engrenamento
49

59. O escorregamento no engrenamento
T1
T2
I
a1
a2 p1
p2
A
B
Figura 40: Escorregamento no engrenamento
De A até I:
• o arco
a1I sobre o perfil p1 é maior que o arco
a2I sobre o perfil
p2;
49

60. O escorregamento no engrenamento
T1
T2
I i1
i2 p1
p2
A
B
Figura 40: Escorregamento no engrenamento
De I até B:
• o arco
i1B sobre o perfil p1 é menor que o arco
i2B sobre o perfil
p2;
Quando o ponto de contacto se dá de A até B, há escorregamento.
49

61. Caminho de A até ao Primitivo
50
T1
T2
I
A
B

62. Caminho do Primitivo até B
51
T1
T2
I
A
B

63. Velocidade linear num ponto M
vM1
vM2
1
2
2
1
T1
T2
O1
O2
M
Figura 41: Velocidade linear num
ponto M
O ponto de contacto M tem as
seguintes velocidades lineares:
Perfil p1:
vM1 = ω1 · O1M = ω1 · rM1
Perfil p2:
vM2 = ω2 · O2M = ω2 · rM2
52

64. Velocidades tangenciais ao cı́rculo de base num ponto M
vM1
vM2
vb1=vb2
1
2
2
1
T1
T2
O1
O2
M
Figura 42: Velocidades na direção do
caminho de engrenamento
vb1 = vM1 ·cos α1 = (ω1 · rM1)·cos α1
vb2 = vM2·cos α2 = (ω2 · rM2)·cos α2
As quantidades:
rM1 · cos α1 = rb1
rM2 · cos α2 = rb2
já são conhecidas
Condição de continuidade de
contacto dos flancos:
vb1 = vb2
ω1 · rM1 · cos α1 = ω2 · rM2 · cos α2
ω1
ω2
= rM2·cos α2
rM1·cos α1
= rb2
rb1
53

65. Velocidades tangenciais à normal do contacto num ponto M
vM1
vM2
v
r
2
v
r
1
1
2
2
1
T1
T2
O1
O2
M
Figura 43: Velocidades tangenciais à
normal do contacto
Velocidades na direção
tangencial ao contacto:
vr1 = vM1 · sin α1 = (ω1 · rM1) · sin α1
vr2 = vM2 · sin α2 = (ω2 · rM2) · sin α2
Também conhecidas por
velocidades de rolamento dos
flancos dos dentes.
A diferença de velocidade de
rolamento do perfil 1
relativamente ao perfil 2, origina
escorregamento.
A existência de atrito e
escorregamento promove perda
de potência (↓ eficiência).
54

66. Cı́rculos Osculadores
v
r
2
v
r
1
1
2
1
2
T1
T2
O1
O2
M
Figura 44: Cı́rculos osculadores
As velocidades de rolamento no
ponto M do pinhão e roda são,
respectivamente:
vr1 = ω1 · rM1 sin α1
vr2 = ω2 · rM2 sin α2
Os perfis podem ser
aproximados por dois cı́rculos
osculadores na vizinhança do
ponto M:
• centro de curvatura em T1 e
raio T1M
• centro de curvatura em T2 e
raio T2M
vr1 = ω1 · T1M vr2 = ω2 · T2M 55

67. Velocidades de escorregamento num ponto M
M vM1
vM2
vb1=vb2
v
r
2
v
r
1
1
2
2
1
T1
T2
O1
O2
Figura 45: Velocidades num ponto M
A velocidade de escorregamento
relativa num ponto M, é dada
por:
vg = vr1 − vr2
É comum representar-se a
velocidade de escorregamento
em módulo:
vg = |vr1 − vr2|
Quantidade útil para efeitos de
cálculo da perda de potência
num ponto M:
PM
vzp = FM
N · vM
g · µM
FM
N - força normal
µM
- coeficiente de atrito
56

68. O escorregamento no engrenamento
57
vM1
vM2
vb1=vb2
v
r
2
v
r
1
1
2
A
B
T1
T2
O1
O2 0 1 2 3 4 5 6 7
AM / mm
0.0
0.5
1.0
1.5
2.0
2.5
3.0
|v
g
|
/
ms
1
Play/Pause

69. O escorregamento especı́fico
T1
T2
a
b
c
d
A
B
Figura 46: Escorregamento especı́fico
A velocidade de escorregamento não é suficiente para caracterizar
as condições de desgaste dos dentes da engrenagem.
gs1 =
ab−
cd
ab
gs2 =
ab−
cd
cd
58

70. O escorregamento especı́fico
v
r
2
v
r
1
1
2
1
2
T1
T2
O1
O2
M
Figura 47: Cı́rculos osculadores e
velocidades tangenciais ao contacto
Sobre o perfil p1:
gs1 =
vr1 − vr2
vr1
gs1 =
ω1 · T1M − ω2 · T2M
ω1 · T1M
Sobre o perfil p2:
gs2 =
vr1 − vr2
vr2
gs2 =
ω1 · T1M − ω2T2M
ω2 · T2M 59

71. O escorregamento especı́fico
A
B
1
2
gs2A
gs1B
T1
T2
O1
O2
I
Figura 48: Escorregamento
especı́fico
gs1 = ω1·T1M−ω2·T2M
ω1·T1M
Quando o contacto se aproxima
de T2, o escorregamento
especı́fico do pinhão,
gs1 → 1 porque T2M → 0
gs2 = ω1·T1M−ω2·T2M
ω2·T2M
Quando o contacto se aproxima
de T1, o escorregamento
especı́fico da roda,
gs2 → 1 porque T1M → 0
60

72. Aula 5

73. Sumário
1. Revisão sobre escorregamento especı́fico 62
2. A correção de dentado para equilibrar escorregamentos
especı́ficos 63
3. Talhagem de engrenagens com correção de dentado 68
4. Importância de igualar os escorregamentos especı́ficos 75
61

74. O escorregamento especı́fico
A
B
1
2
gs2A
gs1B
T1
T2
O1
O2
I
Figura 49: Escorregamento
especı́fico
De notar que a engrenagem com
dentado normal apresenta um
desequilı́brio entre os
escorregamentos especı́ficos, tal
que: gs1B gs2A
Quanto maior for a razão ω1
ω2
= z2
z1
maior será o desequilı́brio.
A solução passa por deslocar AB
na direção do elemento com
menor escorregamento
especı́fico (T2). Tal consegue-se
através da correção de dentado
que promova:
(
r′
a1 ra1
r′
a2 ra2 62

75. Como equilibrar escorregamentos especı́ficos
A0
B0
r
a
1
r
0
a
1
r
a
2
r
0
a
2
1
2
gs2A0
gs1B0
T1
T2
O1
O2
I
Figura 50: Igualar escorregamentos
especı́ficos
Os pontos A e B são definidos
pelos raios de cabeça. Então, a
correção de dentado deverá
afetar os seus valores.
A introdução da “correção de
dentado” x (coeficiente de
desvio ou correção)
r′
a1 = ra1 + x · m
r′
a2 = ra2 − x · m
Antes da Correção:
gs1B gs2A
Depois da Correção:
gs1B′ = gs2A′
63

76. Determinar correção que equilibra gs
O escorregamento especı́fico num ponto de contacto M é dado para
o pinhão gs1 e roda gs2:
gs1 = ω1·T1M−ω2·T2M
ω1·T1M
= 1 − ω2
ω1
· T2M
T1M
gs2 = ω1·T1M−ω2·T2M
ω2·T2M
= ω1
ω2
· T1M
T2M
− 1
T1
T2
I
A
B
Figura 51: Caminho de Engrenamento
No caso particular do Ponto B:
gs1B
= 1 − ω2
ω1
· T2B
T1B
= 1 − z1
z2
· T2B
T1B
No caso particular do Ponto A:
gs2A
= ω1
ω2
· T1A
T2A
− 1 = z2
z1
· T1A
T2A
− 1
Torna-se necessário determinar:
T1B, T1A, T2A, T2B
64

77. Determinação dos Pontos A e B para cálculo de gs
1
2
T1
T2
O1
O2
I
r
a
1
r
a
2
A
B
Figura 52: Caminho de
Engrenamento
T1T2 = T2T1 = O1O2 · sin α = a · sin α
T1A =
√
ra1
2 − rb1
2
T2B =
√
ra2
2 − rb2
2
T2A = T2T1 − T1A = a · sin α −
√
ra1
2 − rb1
2
T1B = T1T2 − T2B = a · sin α −
√
ra2
2 − rb2
2
gs1B = 1 −
z1
z2
·
T2B
T1B
= 1 −
z1
z2
·
√
ra2
2 − rb2
2
a · sin α −
√
ra2
2 − rb2
2
gs2A =
z2
z1
·
T1A
T2A
− 1 =
z2
z1
·
√
ra1
2 − rb1
2
a · sin α −
√
ra1
2 − rb1
2
− 1 65

78. Determinar correção que equilibra gs
A condição existente é gs1B ̸= gs2A
1 −
z1
z2
·
√
ra2
2 − rb2
2
a · sin α −
√
ra2
2 − rb2
2
̸=
z2
z1
·
√
ra1
2 − rb1
2
a · sin α −
√
ra1
2 − rb1
2
− 1
A condição desejável é gs1B′ = gs2A′
1 −
z1
z2
·
q
r′
a2
2
− rb2
2
a · sin α −
q
r′
a2
2
− rb2
2
=
z2
z1
·
q
r′
a1
2
− rb1
2
a · sin α −
q
r′
a1
2
− rb1
2
− 1
1 −
z1
z2
·
q
(ra2 − x · m)2
− rb2
2
a · sin α −
q
(ra2 − x · m)2
− rb2
2
=
z2
z1
·
q
(ra1 + x · m)2
− rb1
2
a · sin α −
q
(ra1 + x · m)2
− rb1
2
− 1
Resolver em ordem a x - única incógnita
O procedimento x2 = −x1 = x demonstrado é devido a Henriot e
usado para Engrenagens com z1 + z2 60
66

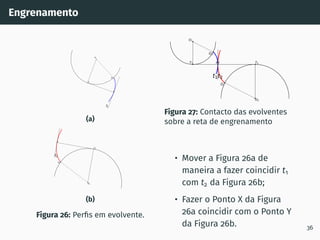
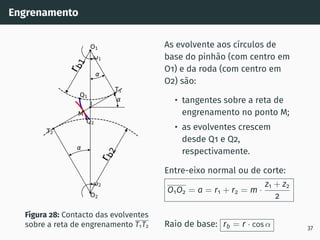
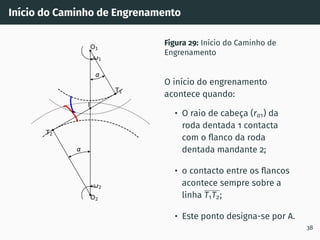
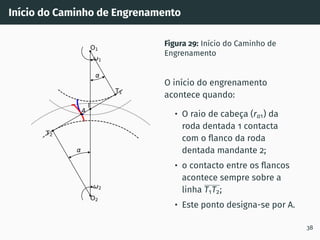
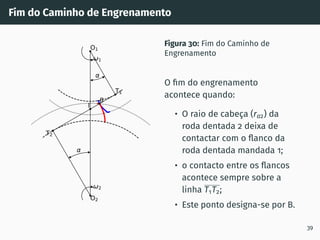
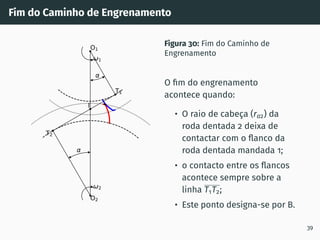
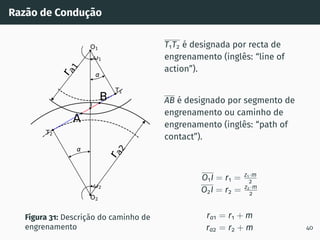
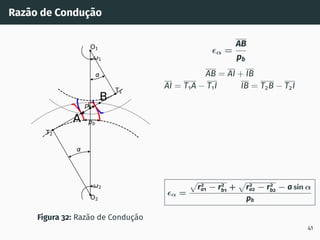
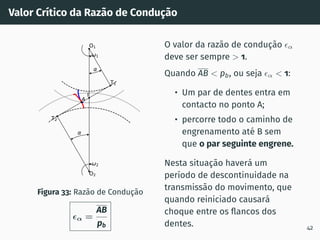
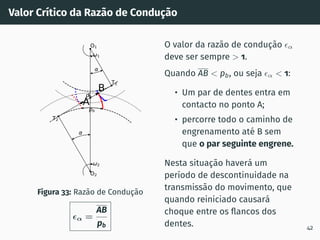
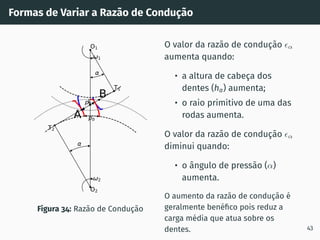
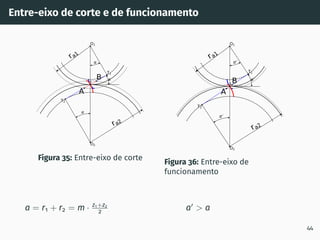
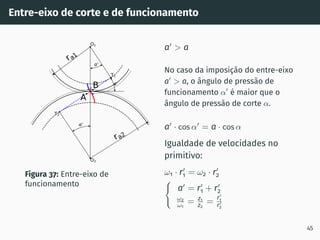
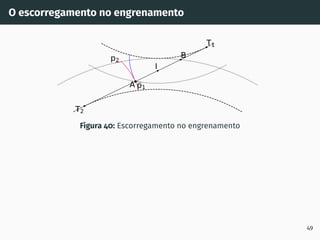
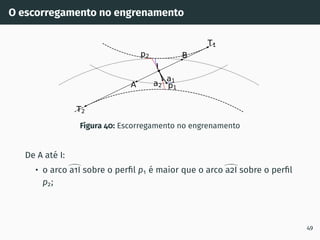
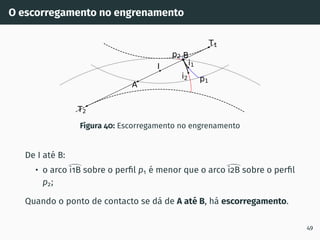
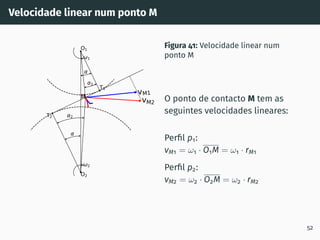
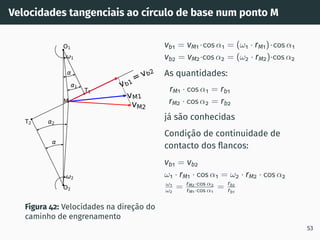
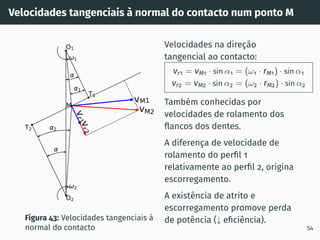
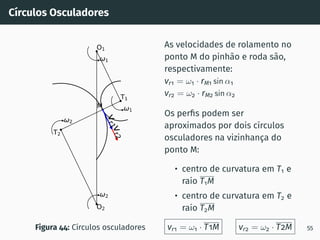
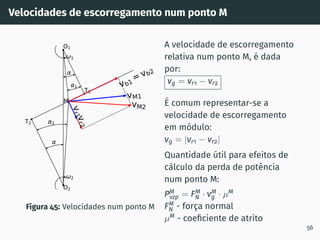
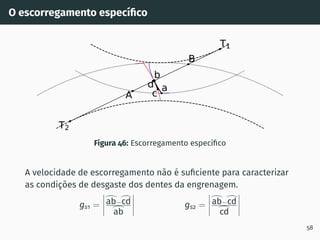
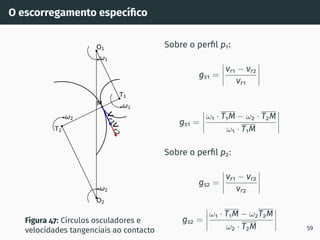
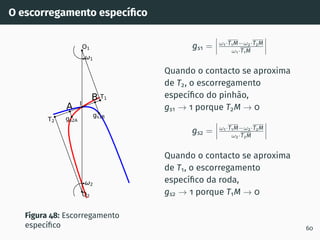
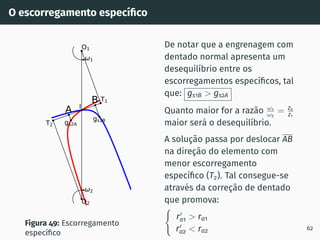
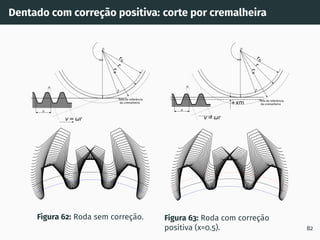
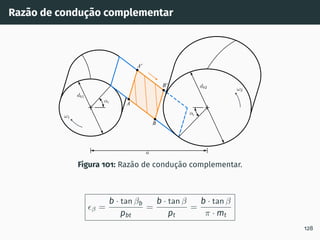
79. Correção de dentado - método gráfico z1 + z2 ≥ 60
Figura 53: Solução gráfica do algoritmo
gs1B′ = gs2A′ [4, 5].
1. Escolher z1 nas
abcissas;
2. Interceptar z1 com a
razão de transmissão
u = z2
z1
(à direita de
ABA’);
3. Escolher x1 nas
ordenadas;
4. x2 = −x1
x1 + x2 = 0
67

80. Correção de dentado positiva
rb
r
r
a
reta de referência
da cremalheira
p
+xm
v= r
O
T
I
Figura 54: Cremalheira com correção positiva. 68

81. Correção de dentado positiva
Geração de dentado por uma cremalheira
z=20.0, m=2.0, x=0.5
=20.0 , haP=1.25, hfP=1.0, =0.38
Figura 55: Forma de um dente com correção positiva.
69

82. Correção de dentado negativa
rb
r
r
a
reta de referência
da cremalheira
p
xm
v= r
O
T
I
Figura 56: Cremalheira com correção negativa.
70

83. Correção de dentado negativa
Geração de dentado por uma cremalheira
z=20.0, m=2.0, x=-0.5
=20.0 , haP=1.25, hfP=1.0, =0.38
Figura 57: Forma de um dente com correção negativa.
71

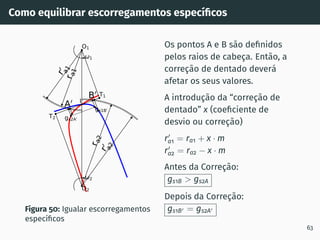
84. Correção de dentado - método gráfico z1 + z2 60
Figura 58: Solução gráfica do algoritmo
gs1B′ = gs2A′ [4, 5].
1. Escolher z1 nas
abcissas;
2. Interceptar z1 com
z1 + z2 = 60;
3. Escolher x1 nas
ordenadas
4. Interceptar z1 com a
razão de transmissão
u = z2
z1
(à esquerda de
ABA’);
5. Escolher x2 nas
ordenadas;
x1 + x2 ̸= 0 – existe
variação de entre-eixo 72

85. Correção de dentado - z1 + z2 60
Como já visto, para z1 + z2 60, a soma das correções
adimensionais é x1 + x2 ̸= 0 e tal implica que existe variação de
entre-eixo.
Utilizando o procedimento para z1 + z2 60, a igualdade dos
escorregamentos especı́ficos também acontecia. No entanto:
• z1 + z2 60 normalmente implicam ter rodas z2 com número de
dentes baixo. Uma correção negativa na roda z2 com um
número de dentes baixo não é recomendado por reduzir a sua
qualidade e enfraquecer o dente;
• o valor máximo do escorregamento especı́fico seria ainda
assim elevado e pouco recomendável.
Henriot propõe então uma solução mais optimizada para
z1 + z2 60 que implica variação do entre-eixo mas minimiza estes
problemas.
73

86. Correção de dentado - z1 + z2 60
Cálculo analı́tico para z1 + z2 60:
1. Criar uma engrenagem hipotética z1 + z2
∗
= 60, sendo z1 o
pinhão da nossa engrenagem de interesse;
2. Impor gs1max = gs2max para a engrenagem hipotética e determinar
x1 = x e x2
∗
= −x, tal como para z1 + z2 60
3. Conhecido x1, impor gs1max
= gs2max
para a engrenagem de
interesse, mas x1 + x2 ̸= 0 e o entre-eixo a′
varia.
4. Resolver o sistema de equações:

















1 − z1
z2
·
√
(ra2+x2·m)2
−rb2
2
a′·sin α′−
√
(ra2+x2·m)2
−rb2
2
= z2
z1
·
√
(ra1+x1·m)2
−rb1
2
a′·sin α′−
√
(ra1+x1m)2
−rb1
2
− 1
a′
· cos α′
= a · cos α
inv α′
= inv α + 2 tan α · x1+x2
z1+z2
74

87. Importância de igualar escorregamento especı́fico
Figura 59: Avaria por gripagem.
Fases da avaria por gripagem:
• Quebra repentina do filme lubrificante;
• Contacto metal-metal;
• Avaria. 75

88. Importância de igualar escorregamento especı́fico
A pressão superficial (Hertz)
entre duas superfı́cies cilı́ndricas
de raio ρ1 e ρ2 é proporcional a:
σH =
r
Fn · E∗
π · b · R
Força normal: Fn
Largura da roda dentada: b
Módulo de Young equivalente:
1
E∗
=
1 − ν2
1
E1
+
1 − ν2
2
E2
Raio de contacto equivalente:
1
R
=
1
ρ1
+
1
ρ2
Em A, inı́cio do engrenamento:
1
RA
= 1
T1A
+ 1
T2A
= T1T2
T1A·T2A
Em B, fim do engrenamento:
1
RB
= 1
T1B
+ 1
T2B
= T1T2
T1B·T2B
O fator de Almen (fator de
gripagem) é o produto da
pressão de contacto pela
velocidade de escorregamento:
σH · vg = σH · (vr1 − vr2)
76

89. Importância de igualar escorregamento especı́fico
Igualdade de escorregamentos especı́ficos:
ω1 · T1B − ω2 · T2B
ω1 · T1B
=
ω2 · T2A − ω1 · T1A
ω2 · T2A
De notar que não deve ser considerada a velocidade de
escorregamento em módulo.
ω2 · T2A · ω1 · T1B − ω2 · T2B
= ω1 · T1B · ω2 · T2A − ω1 · T1A
Após agrupar os termos comuns da velocidade angular da roda (à
esquerda) e do pinhão (à direita):
ω2
2
· T2A · T2B = ω1
2
· T1A · T1B
77

90. Importância de igualar escorregamento especı́fico
Igualdade dos fatores de Almen
do pinhão e roda:
σHB
· vg1B
= σHA
· vg2A
Lembrar que σH =
q
Fn·E∗
π·b·R
A pressão de contacto é
inversamente proporcional à raiz
quadrada do raio de curvatura
equivalente, por isso:
1
RB
1
2
· vg1B
=
1
RA
1
2
· vg2A
T1T2
T1B · T2B
1
2
· ω1 · T1B − ω2 · T2B
=
T1T2
T1A · T2A
1
2
· ω2 · T2A − ω1 · T1A
Após simplificação: ω2
2
· T2A · T2B = ω1
2
· T1A · T1B
Assim se conclui que igualar os escorregamentos especı́ficos
corresponde a igualar os fatores de Almen (risco de gripagem). 78

91. Aula 6

92. Sumário
1. Dentado corrigido 80
2. Cálculo da espessura de dentes corrigidos 85
3. Entre-eixo de rodas corrigidas (x1 + x2 ̸= 0) 86
4. Passo sobre o cı́rculo primitivo de funcionamento 87
5. Cálculo do entre-eixo de funcionamento 90
79

93. Perfil em evolvente com correção
rb
r
a
r
0
a
O
Figura 60: Evolvente de cı́rculo
(correção positiva, x 0).
A roda com correção de dentado
(x ̸= 0) é maquinada com a
mesma ferramenta que a roda
sem correção (x = 0).
O raio de base rb será o mesmo
para ambas as rodas pois
depende apenas do ângulo de
pressão da ferramenta (α).
Podemos concluir que a
evolvente de cı́rculo do raio rb
dá o perfil do dente com (x ̸= 0)
e com (x = 0).
Raio de cabeça sem correção:
ra = r + m
Raio de cabeça com correção:
r′
a = r + m + xm
80

94. Flancos com correção
x0
x=0
x0
círculo primitivo
círculo de base
Figura 61: Comparação de dentado sem correção vs. correção positiva e
negativa.
Na prática a correção de dentado implica mover os perfis sobre o
cı́rculo de base: afastando-os quando a correção é positiva e
aproximando-os quando é negativa. Em inglês, a correção chama-se
de “profile shift”. 81

95. Dentado com correção positiva: corte por cremalheira
rb
r
r
a
reta de referência
da cremalheira
p
v= r
O
T
I
Figura 62: Roda sem correção.
rb
r
r
a
reta de referência
da cremalheira
p
+xm
v= r
O
T
I
Figura 63: Roda com correção
positiva (x=0.5). 82

96. Espessura do dente da cremalheira com correção positiva
reta de referência
da cremalheira
p
i s
+xm
Figura 64: Cremalheira: reta tangente ao cı́rculo primitivo com correção
positiva.
A correção positiva corresponde a afastar a reta de referência da
cremalheira do centro da roda que se pretende fabricar. A
espessura do dente (s) da cremalheira sobre a reta tangente ao
cı́rculo primitivo será menor.
pcremalheira = π · m = s + i com s i (correção positiva)
83

97. Espessura do dente da cremalheira com correção positiva
reta de referência
da cremalheira
p
i s
+xm
Figura 65: Cremalheira: reta tangente ao cı́rculo primitivo com correção
positiva.
scremalheira = π·m
2 − 2 · x · m · tan α icremalheira = π·m
2 + 2 · x · m · tan α
Se a espessura dente do dente da cremalheira sobre a reta tangente
diminui, observa-se um aumento da espessura do dente sobre o
cı́rculo primitivo de referência:
sroda = icremalheira iroda = scremalheira
84

98. Espessura do dente com correção positiva
ra
r
rb
s i
Figura 66: Roda dentada corrigida.
Na roda dentada verifica-se um
aumento da espessura do dente
sobre o cı́rculo primitivo de
corte, mas o passo e o ângulo de
pressão mantêm-se inalterados
(a ferramenta é a mesma).
Assim:
p = π · m = s + i com s i
(correção positiva)
s = π·m
2 + 2 · x · m · tan α
i = π·m
2 − 2 · x · m · tan α
r = z·m
2
ra = r + m + x · m
85

99. Entre-eixo de rodas corrigidas (x1 + x2 ̸= 0)
0
0
0
T1
T2
O1
O2
I
ra1
ra2
r
0
1
r
0
2
Figura 67: Entre-eixo para uma
correção x1 + x2 ̸= 0
Para as situações em que
x1 + x2 ̸= 0 há variação de
entre-eixo.
O1O2 = r′
1 + r′
2
Os raios primitivos de
funcionamento são neste caso
diferentes dos cı́rculos
primitivos de corte, que se
mantêm:
r = z·m
2
O raio de base não se altera,
pois depende apenas do ângulo
de pressão de corte (α):
rb = r · cos α = r′
· cos α′
a′
· cos α′
= a · cos α
86

100. Passo sobre o cı́rculo primitivo de funcionamento
p0
p0
O1
O2
r
0
1
r
0
2
Figura 68: Passo sobre o cı́rculo
primitivo de funcionamento
Sobre os cı́rculos primitivos de
funcionamento:
O passo do pinhão:
p′
= s′
1 + i′
1
O passo da roda:
p′
= s′
2 + i′
2
No entanto, s′
1 = i′
2 e s′
2 = i′
1
Então p′
= s′
1 + s′
2
87

101. Passo sobre o cı́rculo primitivo de funcionamento
i0
2
s0
2
s0
1
i0
1
O1
O2
r
0
1
r
0
2
Figura 68: Passo sobre o cı́rculo
primitivo de funcionamento
Sobre os cı́rculos primitivos de
funcionamento:
O passo do pinhão:
p′
= s′
1 + i′
1
O passo da roda:
p′
= s′
2 + i′
2
No entanto, s′
1 = i′
2 e s′
2 = i′
1
Então p′
= s′
1 + s′
2
87

102. Espessura do dente sobre o cı́rculo primitivo de funcionamento
r
rb
r'
s
s'
Figura 69: Espessura do dente com
correção.
Como determinar r′
?
Não é para já conhecido, mas
podemos escrever s′
1 e s′
2,
espessura do dente sobre o
cı́rculo primitivo de
funcionamento, como:
s′
= r′
·
hs
r
+ 2 · (inv α − inv α′
)
i
No entanto, agora devemos
notar que a roda dentada tem
correção:
s = π·m
2 + 2 · x · m · tan α
i = π·m
2 − 2 · x · m · tan α
r = z·m
2
88

103. Passo sobre o cı́rculo primitivo de funcionamento
i0
2
s0
2
s0
1
i0
1
O1
O2
r
0
1
r
0
2
Figura 70: Passo sobre o cı́rculo
primitivo de funcionamento
r′
1 e r′
2 – Não conhecidos ainda.
No entanto sabemos que o
passo sobre o cı́rculo primitivo
de funcionamento é igual à
soma das espessuras do pinhão
(s′
1) e roda (s′
2):
p′
= s′
1 + s′
2
p′
= r′
1 ·
s1
r1
+ 2 · (inv α − inv α′
)
+ r′
2 ·
s2
r2
+ 2 · (inv α − inv α′
)
89

104. Cálculo do entre-eixo de funcionamento
Dados já conhecidos:
z1, z2, x1, x2, α
No caso de a soma x1 + x2 ̸= 0,
há variação de entre-eixo e
temos 9 incógnitas:
a′
, α′
, r′
1, r′
2, p′
,
s′
1, s′
2, i′
1, i′
2
Sistema de 9 equações:































a′
= r′
1 + r′
2
a′
· cos α′
= a · cos α
2π · r′
1 = z1 · p′
2π · r′
2 = z2 · p′
p′
= s′
1 + i′
1
p′
= s′
2 + i′
2
r′
1 · cos α′
= r1 · cos α = rb1
r′
2 · cos α′
= r2 · cos α = rb2
p′
= s′
1 + s′
2
90

105. Entre-eixo de engrenagens com correção
Correção com variação de entre-eixo
x1 + x2 ̸= 0
(
a′
· cos α′
= a · cos α
inv α′
= inv α + 2 · tan α · x1+x2
z1+z2
Correção sem variação de entre-eixo
x1 + x2 = 0
a′
= a
91

106. Entre-eixo de engrenagens com correção
Para obter inv α′
= inv α + 2 · tan α · x1+x2
z1+z2
, fazer:
(
p′
= s′
1 + s′
2 ⇔ p′
= r′
1 ·
h
s1
r1
+ 2 · (inv α − inv α′
)
i
+ r′
2 ·
h
s2
r2
+ 2 · (inv α − inv α′
)
i
p · cos α = p′
· cos α′
⇔ p′
= p · cos α
cos α′
Igualando as duas equações do sistema:
p · cos α
cos α′ = r′
1 ·
h
s1
r1
+ 2 · (inv α − inv α′
)
i
+ r′
2 ·
h
s2
r2
+ 2 · (inv α − inv α′
)
i
Substituindo r′
1 por r1 · cos α
cos α′ e r′
2 por r2 · cos α
cos α′ :
p· cos α
cos α′ = r1· cos α
cos α′ ·
h
s1
r1
+ 2 · (inv α − inv α′
)
i
+r2· cos α
cos α′ ·
h
s2
r2
+ 2 · (inv α − inv α′
)
i
Recordando que o passo p = π · m e cos α
cos α′ é comum a todos os termos da
equação:
π · m = r1 ·
h
s1
r1
+ 2 · (inv α − inv α′
)
i
+ r2 ·
h
s2
r2
+ 2 · (inv α − inv α′
)
i
Substituindo r1 por z1·m
2
e r2 por z2·m
2
:
π · m = z1·m
2
·
h
π·m/2+2·x1·m·tan α
z1·m
2
+ 2 · (inv α − inv α′
)
i
+ z2·m
2
·
h
π·m/2+2·x2·m·tan α
z2·m
2
+ 2 · (inv α − inv α′
)
i
92

107. Entre-eixo de engrenagens com correção
Simplificando o módulo m por ser comum a todos os termos da
equação:
π = π
2 +2·x1·tan α+z1·(inv α − inv α′
)+π
2 +2·x2·tan α+z2·(inv α − inv α′
)
Agrupando os termos comuns:
π − π
2 − π
2 = 2 · (x1 + x2) · tan α + (z1 + z2) · (inv α − inv α′
)
(z1 + z2) · (inv α′
− inv α) = 2 · (x1 + x2) · tan α
Passando o somatório do número de dentes para o lado direito da
igualdade:
(inv α′
− inv α) = 2 · tan α · x1+x2
z1+z2
Escrevendo a equação em função da inv α′
, c.q.d:
inv α′
= inv α + 2 · tan α ·
x1 + x2
z1 + z2
93

108. Aula 7

109. Sumário
1. Interferência de corte 95
2. Número mı́nimo de dentes para uma roda dentada não
corrigida 98
3. Correção necessária para evitar interferência 100
4. Interferência de engrenamento 102
94

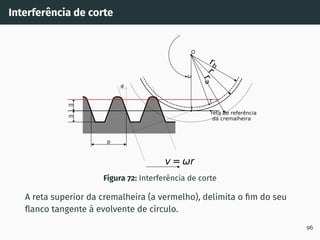
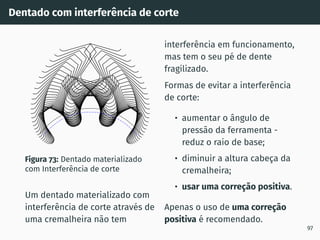
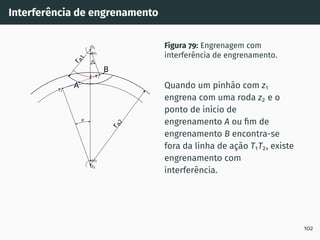
110. Interferência de corte
Figura 71: Interferência de corte [5].
O corte da roda dentada acontece mesmo abaixo do raio de base.
A interferência de corte (em inglês “undercut”) surge quando o
número de dentes da roda dentada é inferior a z′
(ver adiante).
95

111. Interferência de corte
rb
r
r
a
reta de referência
da cremalheira
p
m
m
v= r
O
T
I
Figura 72: Interferência de corte
A reta superior da cremalheira (a vermelho), delimita o fim do seu
flanco tangente à evolvente de cı́rculo.
96

112. Dentado com interferência de corte
Figura 73: Dentado materializado
com Interferência de corte
Um dentado materializado com
interferência de corte através de
uma cremalheira não tem
interferência em funcionamento,
mas tem o seu pé de dente
fragilizado.
Formas de evitar a interferência
de corte:
• aumentar o ângulo de
pressão da ferramenta -
reduz o raio de base;
• diminuir a altura cabeça da
cremalheira;
• usar uma correção positiva.
Apenas o uso de uma correção
positiva é recomendado.
97

113. Número mı́nimo de dentes para uma roda dentada não corrigida
rb
r
r
a
reta de referência
da cremalheira
p
m
m
v= r
O
T
I
Figura 74: Condição limite de interferência de corte
OT · cos α + m = OI
rb · cos α + m = r
r · cos α · cos α + m = r
r · cos2
α + m = r
z′
m
2 · cos2
α + m = z′
·m
2
z′
2 · (cos2
α − 1) = −1
z′
=
2
sin2
α
para α = 20◦
, z′
≈ 17 98

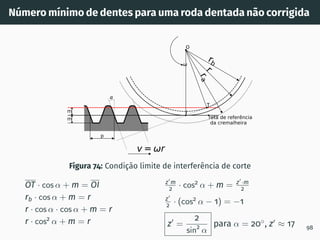
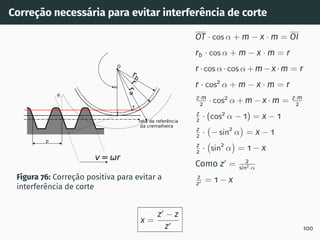
114. Número mı́nimo de dentes para uma roda dentada não corrigida
Figura 75: Método gráfico para
determinar o número mı́nimo de
dentes para uma roda dentada não
corrigida em função do ângulo de
pressão da cremalheira de corte [5].
Se for admissı́vel alguma
interferência e um nı́vel de ruı́do
mais elevado, principalmente a
baixas velocidades, pode-se
usar o número mı́nimo de
dentes correspondente à curva
prática. No entanto é expectável
uma vida útil mais curta.
99

115. Correção necessária para evitar interferência de corte
rb
r
r
a
reta de referência
da cremalheira
p
v= r
O
T
I
Figura 76: Correção positiva para evitar a
interferência de corte
OT · cos α + m − x · m = OI
rb · cos α + m − x · m = r
r ·cos α·cos α+m−x·m = r
r · cos2
α + m − x · m = r
z·m
2 · cos2
α + m − x · m = z·m
2
z
2 · (cos2
α − 1) = x − 1
z
2 · − sin2
α
= x − 1
z
2 · sin2
α
= 1 − x
Como z′
= 2
sin2 α
z
z′ = 1 − x
x =
z′
− z
z′
100

116. Correção positiva para evitar Interferência
Figura 77: Dentado com interferência
de corte
Figura 78: Dentado com correção
x = z′
−z
z′
Com a correção de dentado é possı́vel obter números de dentes
inferiores a z′
, permitindo para a mesma razão de transmissão
u = z2
z1
, obter engrenagens mais compactas. 101

117. Interferência de engrenamento
1
2
T1
T2
O1
O2
I
r
a
1
r
a
2
A
B
Figura 79: Engrenagem com
interferência de engrenamento.
Quando um pinhão com z1
engrena com uma roda z2 e o
ponto de inı́cio de
engrenamento A ou fim de
engrenamento B encontra-se
fora da linha de ação T1T2, existe
engrenamento com
interferência.
102

118. Número mı́nimo de dentes que engrenam sem interferência
1
2
T1 =B
T2
O1
O2
I
r
a
1
r
a
2
A
Figura 80: Engrenagem na condição
limite de interferência de
engrenamento.
T1T2
2
+ O2T2
2
= ra2
2
((r1 + r2) · sin α)
2
+ rb2
2
= ra2
2
z1 = −z2 +
r
z2
2 +
4 · (z2 + 1)
sin2
α 103

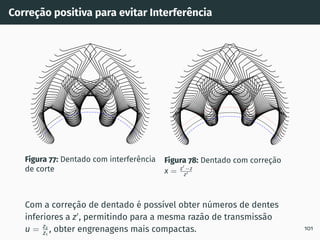
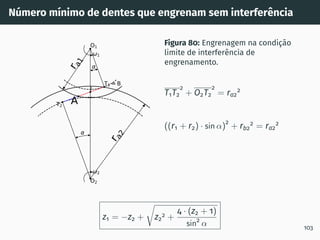
119. Número mı́nimo de dentes z1 em função de z2
Figura 81: Número mı́nimo de dentes do pinhão z1 em função do número de
dentes da roda z2 (ha = m e entre-eixo de corte) [5]. 104

120. Aula 8

121. Sumário
1. Entre-eixo imposto e suas implicações 106
2. Métodos de cálculo das correções de dentado 107
3. Backlash e folga no pé do dente 112
4. Principais modificações de micro-geometria 114
105

122. Entre-eixo imposto e suas implicações
(
a · cos α = a
′
· cos α
′
inv α
′
= inv α + 2 · tan α · x1+x2
z1+z2
Os seguintes métodos/normas apresentam soluções para o
problema da escolha dos valores de x1 e x2, quando
P
x = x1 + x2:
• Igualar fatores de Almen:
• Henriot:
• z1 + z2 60, x1 + x2 = 0, a′ = a
• z1 + z2 60, x1 + x2 ̸= 0, a′ ̸= a
• Equilibrar diferentes critérios e obter engrenagens optimizadas
para uma dada aplicação:
• DIN 3992
• ISO/TR 4467 / NF E 23-013
• BSI – BS PD 6457
106

123. Método DIN 3992
Figura 82: DIN 3992: diagrama para escolha da soma x1 + x2 para
engrenagens redutoras.
1. Escolher a soma z1 + z2 nas abcissas;
2. Selecionar o critério de correção desejado:
• Raio de curvatura: P9 P1 – maior capacidade carga
• Razão de condução: P1 P9
3. Escolher
P
x no eixo das ordenadas.
107

124. Método DIN 3992
Agora que é conhecido z1 + z2 e x1 + x2:
1. Escolher z1+z2
2 nas abcissas e x1+x2
2 nas ordenadas - encontrar ponto de intersecção;
2. Traçar uma linha paralela à linha “Li” mais próxima e que passa pelo ponto definido no
ponto 1;
3. Escolher z1 no eixo das abcissas e intersectar linha definida no ponto 2 - escolhido x1.
Figura 83: DIN 3992: diagrama para escolha da partição de x1 e x2 para
engrenagens redutoras. 108

125. Método ISO/TR 4467 / NF E 23-013
Conhecido z1 e z2, podemos calcular a razão de multiplicação:
u = z2
z1
Utilizar a seguinte expressão para determinar os coeficientes x1 e x2:
(
x1 = λ · u−1
u+1 +
P
x
u+1
x2 =
P
x − x1
Se u 5, usar u = 5.
A razão de transmissão é calculada como i = ωmandante
ωmandada
= zmandada
zmandante
Para engrenagens redutoras, i.e. i 1, usar
0.5 ≤ λ ≤ 0.75
Para engrenagens multiplicadoras, i.e. i 1, usar
0.0 ≤ λ ≤ 0.5 – Henriot preconiza o uso de λ = 0 para obter engrenagens
mais eficientes. 109

126. Método BSI – BS PD 6457
Conhecido z1 e z2, podemos calcular a razão de multiplicação:
u = z2
z1
Utilizar a seguinte expressão para determinar os coeficientes x1 e x2:
(
x1 = C · u−1
u +
P
x
u+1
x2 =
P
x − x1
Igualar flexão no pé do dente:
C = 1
2
Igualar escorregamentos especı́ficos:
C = 1
√
zv1
, com zv1 = z1
cos3 β , para engrenagens de dentado reto é
zv1 = z1
110

127. Exemplo de Aplicação
Exemplo:
z1 = 20, z2 = 41, α = 20◦
, m = 2 mm
Engrenagem redutora com u = z2
z1
= |i| = 2.05
z1 + z2 = 61
Consideremos para todos os métodos que não há variação de
entre-eixo: x1 + x2 = 0
Parâmetro Normal Igualar gs Ábaco Henriot DIN 3992 ISO TR 4467 BSI BS PD 6457
Metodologia - gs1B = gs2A Gráfico Gráfico λ = 0.75 C = 0.5
x1 0 0.251 0.240 0.100 0.258 0.256
x2 0 -0.251 -0.240 -0.100 -0.258 -0.256
gs1B 4.270 1.989 2.053 3.092 1.949 1.961
gs2A 1.487 1.989 1.965 1.678 2.004 1.999
De notar que, exceto o procedimento DIN 3992, todos os restantes
métodos apresentam resultados similares quando se considera
como critério equilibrar os escorregamentos especı́ficos.
111

128. Backlash
As correções de dentado, tal como visto anteriormente, assumiam a
inexistência de backlash.
Na prática, as engrenagens
deverão ter backlash de forma a
acomodar os seguintes efeitos:
• presença de erros de
fabrico;
• expansão térmica;
• deformação do dentado sob
carga;
• lubrificação.
Figura 84: Backlash.
jt = 2 · ∆a′
· tan α′
→ backlash radial
a′
− ∆a′
= m · z1+z2
2 · cos α
cos α′
Existe a necessidade de reajustar as correções de dentado x1 e x2 para
incluir o backlash.
112

129. Folga no pé do dente
Folga entre a cabeça e o pé do
dente (em inglês “tip clearance”)
é representado por c1 e c2 para o
pinhão e roda, respetivamente.
Figura 85: Folga no pé do dente (ISO
21771).
A introdução de correções de dentado alteram a folga entre o pé de
dente e o raio de cabeça da roda conjugada.
De modo a garantir um valor adequado de folga, é aplicado o fator
adimensional (k) de redução dos raios de cabeça:
k =
z1 + z2
2
·
inv α′
t − inv αt
tan α
−
1
cos β
·
cos αt
cos α′
t
− 1
O novo raio de cabeça será: ra = r + m · (ha + x − k) 113

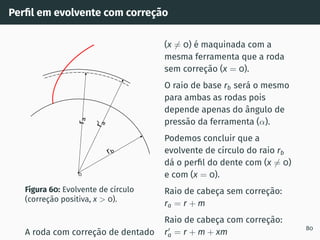
130. Principais modificações de micro-geometria
Figura 86: Tip and root relief Figura 87: End relief
O alı́vio da cabeça (tip relief) e o alı́vio do pé do dente (root relief)
são modificações intencionais do perfil do dente. Uma pequena
quantidade de material é removido com a finalidade de suavizar o
inı́cio do engrenamento [5]. O end relief evita o contacto nos bordos
das rodas dentadas.
As modificações micro-geométricas do tipo relief podem ser:
lineares, arcos, progressivas... (Ver ISO 21771)
114

131. Principais modificações de micro-geometria
Figura 88: Profile crowning Figura 89: Lead crowning
Na prática, as engrenagens possuem desvios e erros de
fabrico/montagem.
Para reduzir tanto quanto possı́vel os efeitos destes desvios e erros,
tipicamente usam-se modificações do perfil nas direção do perfil
(profile crowning) e longitudinal (lead crowning) [5].
Existem outras modificações que permitem modificação do ângulo
de pressão e hélice (helicoidais).
115

132. Aula 9

133. Sumário
1. A engrenagem helicoidal 117
2. Número virtual de dentes 126
3. Razão de condução de engrenagens helicoidais 127
116

134. Engrenagem helicoidal
Figura 90: Engrenagem helicoidal e
classificação da inclinação da hélice.
Ângulo de hélice
O ângulo de hélice é
denominado por β, e
pode ter inclinação à
direita ou à esquerda.
Os valores comuns do
ângulo de hélice estão
compreendidos entre 15 e
45◦
.
O uso de valores
elevados de β introduz
cargas axiais
significativas.
117

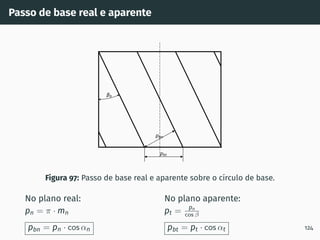
135. Elementos geométricos no plano real
Figura 91: Ângulo de pressão sobre o
plano real ou normal -
perpendicular ao dentado [5].
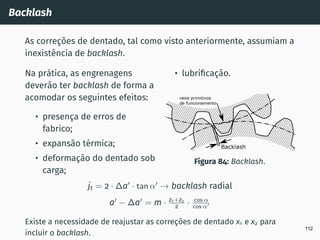
Elementos reais:
medem-se num plano
perpendicular ao dentado e
representam-se pelo ı́ndice n
αn ângulo de pressão real
mn módulo real
pn passo real
pbn passo de base real
pn = π · mn
pbn = pn · cos αn
118

136. Elementos geométricos no plano aparente
Figura 92: Ângulo de pressão sobre o
plano aparente ou transversal -
perpendicular ao eixo da roda
dentada [5].
Elementos aparentes:
medem-se num plano
perpendicular aos eixos da
engrenagem e representam-se
pelo ı́ndice t
αt ângulo de pressão aparente
mt módulo aparente
pt passo aparente
pbt passo de base aparente
119

137. Plano aparente – raios de base, primitivo, cabeça e pé
t
t
T1
T2
O1
O2
I
r
1
r
2
r
b
1
r
b
2
Figura 93: Plano aparente ou
transversal - perpendicular ao eixo
da roda dentada.
Raio de base:
rb = r · cos αt
Raio primitivo:
2 · π · r = z · pt
r = z·pt
2π = z·mt
2
Utilizando um perfil de
referência tipo A (ISO 53)
Raio de cabeça:
ra = r + mn
Raio de pé:
rd = r − 1.25 · mn
120

138. Hélice primitiva e hélice de base
hélice de base
hélice primitiva
Figura 94: Hélice primitiva e hélice
de base.
O ângulo de hélice β é avaliado
sobre o cı́rculo primitivo.
O ângulo de hélice de base βb é
avaliado sobre o cı́rculo de base.
O passo de hélice pz é igual para
o cı́rculo de base e para o cı́rculo
primitivo.
121

139. Relação entre ângulo de hélice primitiva e de base
2 r
2 rb
pz
b
Figura 95: Relação entre ângulos de
hélice.
Planificando o cilindro primitivo
e o cilindro de base, podemos
conhecer a relação do passo de
hélice pz, comum às duas
hélices, com o perı́metro dos
dois cilindros:
pz · tan βb = 2 · π · rb
pz · tan β = 2 · π · r
pz = 2·π·r·cos αt
tan βb
= 2·π·r
tan β
cos αt
tan βb
= 1
tan β
tan β · cos αt = tan βb
122

140. Passo real e aparente
pt
pn
px
Figura 96: Passo real, aparente e axial sobre o cı́rculo primitivo.
No plano real:
pn = π · mn
Mas:
pt ̸= pn
pt · cos β = pn
pt =
pn
cos β
mt · cos β = mn
mt =
mn
cos β 123

141. Passo de base real e aparente
pbt
pbn
b
Figura 97: Passo de base real e aparente sobre o cı́rculo de base.
No plano real:
pn = π · mn
pbn = pn · cos αn
No plano aparente:
pt = pn
cos β
pbt = pt · cos αt 124

142. Relação entre ângulo de pressão aparente e real
Figura 98: Corte A-A: plano aparente;
corte B-B: plano real [6].
No plano real:
lk = pn/2
tan αn
No plano aparente:
tan αt = pt/2
lk
A altura lk é comum aos dois
planos, então:
tan αt = pt/2
pn/2
tan αn
A razão entre o passo aparente
pt e o passo real pn é:
pt = pn
cos β
Então:
tan αt =
pn
cos β
pn
tan αn
tan αt =
tan αn
cos β
125

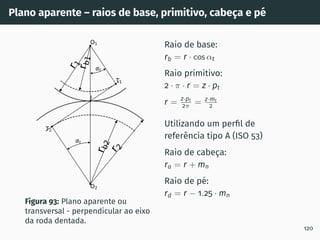
143. Número virtual de dentes
Figura 99: Número virtual de dentes [6].
dn = 2·r
cos2 β = zv · mn, sendo mn = mt · cos β e 2·r
mt
= z
zv =
z
cos3 β
Para determinação das correções de dentado nos ábacos previamente
apresentados, deverá ser usado o número virtual de dentes. 126

144. Razão de condução de engrenagens helicoidais
pbt
b tan b
b
Figura 100: Razão de condução
complementar.
A razão de condução de uma
engrenagem helicoidal é
determinada pela soma de duas
componentes:
ϵ = ϵαt
+ ϵβ
ϵαt = AB
pbt
ϵβ tem a denominação de razão
de condução complementar
ϵβ =
b · tan βb
pbt
=
b · tan β
pt
=
b · tan β
π · mt
127

145. Razão de condução complementar
t
t
B
A
A'
B'
Figura 101: Razão de condução complementar.
ϵβ =
b · tan βb
pbt
=
b · tan β
pt
=
b · tan β
π · mt
128

146. Razão de condução complementar
Figura 102: Razão de condução
complementar.
ϵβ = ϕ
pbt/rb
=
r·ϕ·
rb
r
pbt
ϵβ = b·tan β·cos αt
pt·cos αt
= b·tan β
π·mt
ϵβ =
b · tan β
πmt
129

147. Aula 10

148. Sumário
1. Introdução à capacidade de carga de engrenagens 131
2. Flexão no pé do dente 137
3. Pressão de contacto 139
4. A normalização no cálculo da capacidade de carga 142
130

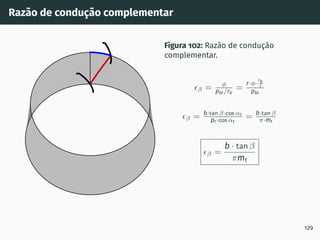
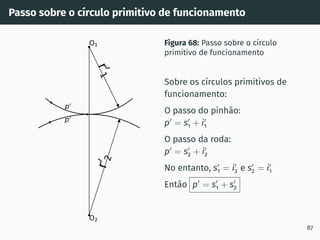
149. Introdução à capacidade de carga de engrenagens
Figura 103: Forças que atuam sobre
uma engrenagem helicoidal de
hélice direita [7].
Análise de forças
Força tangencial (normalmente
conhecida):
Ft = Mt
r = P
v
Força normal:
Fn = Ft
cos αt
Força radial:
Fr = Ft · tan αt
Força axial (apenas helicoidais):
Fa = Ft · tan β
Força total:
F = Ft
cos αn·cos β
131

150. Introdução à capacidade de carga de engrenagens
Na prática de engenharia, é necessário conhecer qual a potência ou
binário que uma engrenagem transmite sem danificar o dentado [8].
Figura 104: Padrão de tensões numa
engrenagem de dentado reto obtido
por foto-elasticidade [8].
Através da Figura 104 podemos
verificar que as tensões
máximas observam-se na zona
de contacto e na zona do pé de
dente onde o momento fletor é
máximo.
Há então duas componentes que
limitam a capacidade de carga
de uma engrenagem:
1. flexão e fadiga no pé do
dente
2. pressão de contacto
132

151. Introdução à capacidade de carga de engrenagens
ra
r rb
F
rd
s
Figura 105: Modelo simplificado para
a flexão no pé de dente.
Sendo b a largura da roda
dentada, o dente é aproximado
por uma viga de secção s × b e
altura h:
h = ra − rd = 2.25 · m
A força tangencial é calculada a
partir do momento torsor Mt:
F = Ft = Mt
r
O momento fletor no pé de
dente de raio rd é:
Mf = Ft · h
ymax = s
2
I = b·s3
12
A tensão máxima, que ocorre no
pé do dente (tração à direita,
compressão à esquerda), é:
σ =
Mf ·ymax
I 133

152. Introdução à capacidade de carga de engrenagens
Para uma roda dentada sem correção de dentado, x = 0, sabemos
que s = π·m
2
σ =
Ft · h · s
2
b·s3
12
=
6 · Ft · h
b · s2
=
6 · Ft · 2.25 · m
b · π·m
2
2 =
54 · Ft
π2 · b · m
=
5.471 · Ft
b · m
≤ σadm
Se expressarmos a largura b em função do módulo b = k · m,
poderemos escrever uma equação para escolha do módulo m:
5.471 · Ft
k · m2
≤ σadm ⇔ m ≥
s
5.471 · Ft
k · σadm
Como é evidente, este modelo não é utilizado na prática corrente.
134

153. A Fórmula de Lewis
Figura 106: Modelo de Lewis para a flexão no pé de dente [8].
Considerações:
• inscrever uma parábola de igual resistência à flexão no dente;
• carregamento atua na cabeça do dente;
• toda a carga é suportada por apenas um par de dentes;
• não foi considerado o efeito de concentração de tensões.
135

154. A Fórmula de Lewis
Figura 107: Modelo de Lewis para a
flexão no pé de dente [8].
σ =
Ft·h· t
2
b·t3
12
= 6·Ft·h
b·t2
Por triângulos similares:
t/2
x = h
t/2 ⇔ t2
h = 4 · x
Definindo y = 4·x
6·π·m e Y = 1
π·y
Para α = 20◦
, y = 0.154 − 0.912/z [9].
σ = 6·Ft
b·4·x = Ft
π·b·m·y = Ft
b·m · Y
Escrevendo a força tangencial
como função do momento torsor
Ft = Mt
r e a largura como função
do módulo b = k · m:
σ =
Mt
z·m
2
π·k·m·m·y ≤ σadm
m ≥ 3
s
2 · Mt
π · k · z · y · σadm
136

155. Flexão no pé do dente
Figura 108: Definição ISO da secção
resistente sFn [6].
σb = (Ft·hFa)·(sFn/2)
b·sFn
3
12
=
(FN·cos α′
a·hFa)·(sFn/2)
b·sFn
3
12
=
6·FN·cos α′
a·hFa
b·sFn
2
σ =
Ft
b · m
·
6 ·
hFa
m
· cos α′
a
sFn
m
2
· cos α
=
Ft
b · m
· YF
137

156. Força normal no caminho de engrenamento
A I B
0.0
0.2
0.4
0.6
0.8
1.0
1.2
F
n
Figura 109: Partição de carga normal
ao dente ao longo do caminho de
engrenamento para uma
engrenagem de dentado reto.
De notar que a carga aplicada no
dente varia ao longo do caminho
de engrenamento. Até agora foi
considerado que apenas um par
de dentes se encontra em
contacto, para determinação da
tensão máxima. No entanto,
quando o contacto se dá sobre a
cabeça do dente, ponto A ou B,
existe 2 pares de dentes em
contacto. Então:
σb =
Ft
b · m
· YF · Yϵ
com Yϵ = 1
ϵα
138

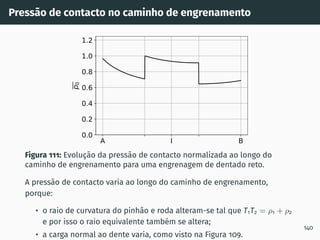
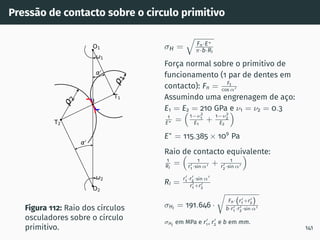
157. Pressão de contacto
σH =
r
Fn · E∗
π · b · R
Figura 110: Pressão de contacto de
Hertz [5].
Força normal:
Fn
Largura da roda dentada:
b
Módulo de Young equivalente:
1
E∗ =
1−ν2
1
E1
+
1−ν2
2
E2
Raio de contacto equivalente:
1
R =
1
ρ1
+ 1
ρ2
Para efeito do dimensionamento às avarias superficiais, a abordagem ISO
6336:2 considera a pressão de contacto no ponto primitivo.
139

158. Pressão de contacto no caminho de engrenamento
A I B
0.0
0.2
0.4
0.6
0.8
1.0
1.2
p
0
Figura 111: Evolução da pressão de contacto normalizada ao longo do
caminho de engrenamento para uma engrenagem de dentado reto.
A pressão de contacto varia ao longo do caminho de engrenamento,
porque:
• o raio de curvatura do pinhão e roda alteram-se tal que T1T2 = ρ1 + ρ2
e por isso o raio equivalente também se altera;
• a carga normal ao dente varia, como visto na Figura 109.
140

159. Pressão de contacto sobre o circulo primitivo
1
2
0
0
1
2
T1
T2
O1
O2
I
Figura 112: Raio dos cı́rculos
osculadores sobre o cı́rculo
primitivo.
σH =
q
Fn·E∗
π·b·RI
Força normal sobre o primitivo de
funcionamento (1 par de dentes em
contacto): Fn = Ft
cos α′
Assumindo uma engrenagem de aço:
E1 = E2 = 210 GPa e ν1 = ν2 = 0.3
1
E∗ =
1−ν2
1
E1
+
1−ν2
2
E2
E∗
= 115.385 × 109
Pa
Raio de contacto equivalente:
1
RI
=
1
r′
1 ·sin α′ + 1
r′
2·sin α′
RI =
r′
1 ·r′
2·sin α′
r′
1 +r′
2
σHI = 191.646 ·
r
Fn·(r′
1 +r′
2)
b·r′
1 ·r′
2·sin α′
σHI
em MPa e r′
1 , r′
2 e b em mm.
141

160. A normalização no cálculo da capacidade de carga
As seguintes entidades têm apresentado sucessivas normas sobre a
capacidade de carga de engrenagens: AFNOR (França), AGMA (EUA),
BSI (Reino Unido), DIN (Alemanha), ISO (Internacional)...
As principais normas de cálculo da capacidade de carga de
engrenagens:
• Alemanha
• DIN 3990:1987 – “CALCULATION OF LOAD CAPACITY OF CYLINDRICAL
GEARS”
• EUA
• AGMA 2101-D04 – “Fundamental Rating Factors and Calculation
Methods for Involute Spur and Helical Gear Teeth”
• Internacional
• ISO 6336:1996; ISO 6336:2006; ISO 6336:2019 – “Calculation of load
capacity of spur and helical gears”
142

161. Aula 11

162. Sumário
1. A norma ISO 6336 144
2. ISO 6336-1: Considerações Gerais 145
3. ISO 6336-2: Pressão de contacto 147
4. ISO 6336-3: Fadiga e flexão no pé do dente 149
5. Eficiência em caixas de engrenagens 152
143

163. A norma ISO 6336
Tabela 1: ISO 6336:2019 [10]
Calculation of load capacity of spur and helical gears International Standard Technical Specification Technical Report
Part 1: Basic principles, introduction and general in-
fluence factors
X
Part 2: Calculation of surface durability (pitting) X
Part 3: Calculation of tooth bending strength X
Part 4: Calculation of tooth flank fracture load capa-
city
X
Part 5: Strength and quality of materials X
Part 6: Calculation of service life under variable load X
Part 20: Calculation of scuffing load capacity (also
applicable to bevel and hypoid gears) — Flash tem-
perature method (replaces: ISO/TR 13989-1)
X
Part 21: Calculation of scuffing load capacity (also ap-
plicable to bevel and hypoid gears) — Integral tem-
perature method (replaces: ISO/TR 13989-2)
X
Part 22: Calculation of micropitting load capacity (re-
places: ISO/TR 15144-1)
X
Part 30: Calculation examples for the application of
ISO 6336 parts 1,2,3,5
X
Part 31: Calculation examples of micropitting load
capacity (replaces: ISO/TR 15144-2)
X
144

164. ISO 6336-1: Considerações Gerais
A norma ISO 6336 aplica-se às seguintes situações [11, 12, 10]:
• ângulo de pressão entre 15 e 25 ◦
;
• ângulo de hélice até 30 ◦
;
• engrenagens de dentado reto ou helicoidal com razão de
condução 1 ϵα 2.5;
A norma ISO 6336 não se aplica às seguintes situações [11, 12, 10]:
• engrenagens de dentado reto ou helicoidal com razão de
condução ϵα 1;
• caso exista interferência entre a cabeça e o pé do dente;
• dentado pontiagudo;
• engrenagens sem “backlash”.
Estas normas são também desaconselhadas para aplicação em
engrenagens não metálicas. Para engrenagens poliméricas, existem
guias de cálculo especı́ficos: VDI 2545 (1981) e VDI 2736 (2016).
145

165. ISO 6336-1: Considerações Gerais
Métodos de cálculo de acordo com a ISO 6336:1996:
A - fatores derivados de modelação numérica (MEF) e experimentação
(pouco usado);
B - fatores derivados com boa precisão para a maioria das aplicações com
base num modelo geométrico rigoroso;
C - fatores aproximados por relações simplificadas, devendo sempre
verificar-se as condições de aplicabilidade.
As edições ISO 6336:2006 e ISO 6336:2019 usam apenas os métodos A e B.
Para se ter acesso ao método C, útil para o cálculo da flexão e fadiga no pé
do dente recorrendo a informação na forma de gráficos, devemos consultar
a mais antiga edição da norma ISO 6336-3:1996.
146

166. ISO 6336-2 [13]: Pressão de contacto
Pressão de contacto nominal
(“nominal contact stress at pitch
point”):
σH0 = ZH · ZE · Zϵ · Zβ ·
q
Ft
d1·b · u+1
u
ZH zone factor Zϵ contact ratio factor
ZE elasticity factor Zβ helix angle factor
Pressão de contacto
(“contact stress”):
σH = ZB · σH0 ·
p
KA · KV · KHβ · KHα
σH ≤ σHP
ZB pinion single pair tooth contact factor
KA application factor
KV dynamic factor
KHβ face load factor for contact stress
KHα transverse load factor for contact stress
Figura 113: Zone factor ZH = Y para
α = 20◦
, escolher nas abcissas
ângulo de hélice β [13]. 147

167. ISO 6336-2: Pressão de contacto
σHP =
σHlim
· ZNT
SHmin
· ZL · ZV · ZR · ZW · ZX =
σHG
SHmin
σHP permissible contact stress
σHlim
allowable stress number from reference test gears (ISO 6336:5)
σHG contact stress limit
ZNT life factor
ZL lubricant factor
ZV velocity factor
ZR roughness factor
ZW work hardening factor
ZX size factor
SHmin
= 1 minimum safety factor
SH safety factor
SH =
σHG
σH
≥ SHmin 148

168. ISO 6336-3:1996 [14] – Fadiga e flexão no pé do dente
Tensão nominal no pé do dente
(“Nominal tooth root stress”):
σF0 = Ft
b·mn
· YFa · YSa · Yϵ · Yβ
Método C que assume a carga
aplicada na cabeça do dente.
YFa form factor
YSa stress correction factor
Yϵ contact ratio factor
Yβ helix angle factor
Tensão no pé do dente
(“Tooth root stress”):
σF = σF0 · KA · KV · KFβ · KFα ≤ σFP
KA application factor
KV dynamic factor
KFα transverse load factor for tooth root stress
KFβ face load factor for tooth root stress
Figura 114: Fator de forma YFa para
hfP = 1.25 · m, haP = m, ρfP = 0.25 · m
[14].
149

169. ISO 6336-3: Fadiga e flexão no pé do dente
σFP =
σFlim
· YST · YNT
SFmin
· YδrelT · YRrelT · YX =
σFG
SFmin
σFP permissible bending stress
σFlim
nominal stress number from reference test gears (ISO 6336:5)
σFG tooth-root stress limit
YST stress correction factor
YNT life factor for tooth-root stress
YδrelT relative notch sensitivity factor
YRrelT relative surface factor
YX size factor
SFmin
= 1.4 minimum safety factor
SF safety factor
SF =
σFG
σF
≥ SFmin
150

170. ISO 6336: Resumo do procedimento de cálculo
1. Determinar a tensão nominal σH0 e σF0 – cálculo estático
idealizado;
2. Determinar os factores de influência pela seguinte ordem:
• fator da aplicação KA;
• fator dinâmico KV considerando Ft · KA;
• fator de distribuição de carga longitudinal KHβ ou KFβ
considerando Ft · KA · KV;
• fator de distribuição de carga transversal KHα ou KFα
considerando Ft · KA · KV · KHβ ou Ft · KA · KV · KFβ;
3. Cálculo da tensão corrigida σH e σF: multiplicar a tensão
nominal pelos fatores de influência;
4. Comparar a tensão corrigida σH e σF com a tensão limite σHG e
σFG e calcular os fatores de segurança.
151

171. Eficiência em caixas de engrenagens
PV = PVZ0 + PVZP + PVL + PVD
independentes da carga
dependentes da carga
perda de potência engrenangens rolamentos vedantes
Höhn et al. [15]
PVZ0 PVZP PVL PVD
Velocidade de rotação Potência nominal Potência nominal Velocidade de rotação
Geometria do cárter Geometria da engrenagem Geometria do rolamento Diâmetro do vedante
Viscosidade do lubrificante Lubrificante Lubrificante Viscosidade do lubrificante
152

172. Eficiência em caixas de engrenagens
Perda de potência devido à carga numa engrenagem PVZP
(Ohlendorf [16]):
PVZP = Pin · HVL · µmZ
Pin – potência nominal; HVL – fator geométrico de perdas; µmZ – coeficiente de atrito médio
HVL =
π·(u+1)
z1·u·cos βb
1 − ϵα + ϵ1
2
+ ϵ2
2
u = z2
z1
ϵα = AB
pbt
ϵ1 = AI
pbt
ϵ2 = IB
pbt
µmZ = 0.048 ·
Fbt
b·
P
vri
·Ri
0.2
· η−0.05
· Ra
0.25
· XL
Fbt =
Mt
rb
força tangencial ao cı́rculo de base [N]
b largura da engrenagem [mm]
P
vri
= vr1 + vr2 soma da velocidade no ponto primitivo [m/s]
Ri =
1
r′
1·sin α′ + 1
r′
2·sin α′
−1
raio equivalente no ponto primitivo [mm]
η viscosidade dinâmica do lubrificante [mPa s]
Ra rugosidade média das superfı́cie (valor tı́pico 0.5) [µm]
XL parâmetro dependente do lubrificante [17]:
Mineral sem aditivos: XL = 1 Mineral com aditivos: XL = 0.85 Sintético com aditivos: XL = 0.65
153

173. Referências

174. Referências i
[1] DIN 3998-1: Denominations on Gears and Gear Pairs: General
Definitions.
1976.
[2] Okorn, Ivan, Marko Nagode e Jernej Klemenc: Operating
performance of external non-involute spur and helical gears: A
review.
Strojniski Vestnik/Journal of Mechanical Engineering,
67(5):256–271, 2021, ISSN 00392480.
[3] Goldfarb, Veniamin, Evgenii Trubachev e Natalya Barmina:
Advanced Gear Engineering, volume 51 de Mechanisms and
Machine Science.
Springer International Publishing, 2018,
ISBN 978-3-319-60398-8.
154

175. Referências ii
[4] Henriot, G.: Traité théorique et pratique des engrenages.
Dunod, 1961, ISBN 2.04.005836.2.
[5] Vullo, Vincenzo: Gears, volume 10 de Springer Series in Solid
and Structural Mechanics.
Springer International Publishing, Cham, 2020,
ISBN 978-3-030-38631-3.
[6] Haberhauer, Horst: Maschinenelemente.
Springer Berlin Heidelberg, Berlin, Heidelberg, 2018.
[7] Budynas, Richard G. e J. Keith Nisbett: Shigley’s Mechanical
Engineering Design.
10a
edição, 2014, ISBN 978-0-07-339820-4.
155

176. Referências iii
[8] Juvinall, Robert C. e Kurt M. Marshek: Fundamentals of Machine
Component Design.
Wiley, 2017.
[9] Castro, Paulo M. S. Tavares de e Sérgio M. O. Tavares:
Capacidade de carga das rodas dentadas.
Órgãos de Máquinas, DEMec, Faculdade de Engenharia da
Universidade do Porto, 2013.
[10] ISO 6336-1:2019: Calculation of load capacity of spur and helical
gears - Part 1: Basic principles, introduction and general
influence factors.
2019.
156

177. Referências iv
[11] ISO 6336:1996: Calculation of load capacity of spur and helical
gears - Part 1: Basic principles, introduction and general
influence factors.
1996.
[12] ISO 6336:2006: Calculation of load capacity of spur and helical
gears - Part 1: Basic principles, introduction and general
influence factors.
2006.
[13] ISO 6336-2:2006: Calculation of load capacity of spur and
helical gears. Part 2: Calculation of surface durability (pitting).
2006.
[14] ISO 6336-3:1996: Calculation of load capacity of spur and helical
gears. Part 3: Calculation of tooth bending strength.
1996.
157

178. Referências v
[15] Höhn, B. R., Klaus Michaelis e T. Völlmer: Thermal Rating of
Gear Drives Balance Between Power Loss and Heat Dissipation.
AGMA Technical Paper, 96:12, 1996.
[16] Ohlendorf, H: Verlustleistung und Erwärmung von Stirnrädern.
Tese de Doutoramento, Dissertation TU München, 1958.
[17] Fernandes, Carlos M.C.G., Pedro M.T. Marques, Ramiro C. Martins
e Jorge H.O. Seabra: Gearbox power loss. Part II: Friction losses
in gears.
Tribology International, 88:309–316, 2015.
158