Razoes trig
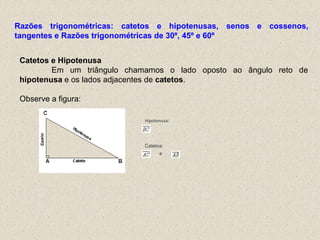
- 1. Hipotenusa: Catetos: e Catetos e Hipotenusa Em um triângulo chamamos o lado oposto ao ângulo reto de hipotenusa e os lados adjacentes de catetos. Observe a figura: Razões trigonométricas: catetos e hipotenusas, senos e cossenos, tangentes e Razões trigonométricas de 30º, 45º e 60º
- 2. Hipotenusa: “a” Catetos: “b” e “c” Seno, Cosseno e Tangente Considere um triângulo retângulo BAC: Ângulos: Tomando por base os elementos desse triângulo, podemos definir as razões trigonométricas seno, cosseno e tangente.
- 3. Seno de um ângulo agudo é a razão entre a medida do cateto oposto a esse ângulo e a medida da hipotenusa. Assim:
- 4. Cosseno de um ângulo agudo é a razão entre a medida do cateto adjacente a esse ângulo e a medida da hipotenusa. Assim:
- 5. Tangente de um ângulo agudo é a razão entre a medida do cateto oposto e a medida do cateto adjacente a esse ângulo. Assim:
- 6. Exemplo: Observações: 1. A tangente de um ângulo agudo pode ser definida como a razão entre seno deste ângulo e o seu cosseno. 2. A tangente de um ângulo agudo é um número real positivo. 3. O seno e o cosseno de um ângulo agudo são sempre números reais positivos menores que 1, pois qualquer cateto é sempre menor que a hipotenusa.
- 7. As razões trigonométricas de 30º, 45º e 60º Considerando as figuras: Verificaremos o seno, cosseno e tangente dos ângulos 30º, 45º e 60º. Quadrado de lado l e diagonal Triângulo equilátero de lado l e altura
- 8. Seno, cosseno e tangente de 30º Aplicando as definições de seno, cosseno e tangente para os ângulos de 30º, temos:
- 9. Seno, cosseno e tangente de 45º Aplicando as definições de seno, cosseno e tangente para um ângulo de 45º, temos:
- 10. Seno, cosseno e tangente de 60º Aplicando as definições de seno, cosseno e tangente para um ângulo de 60º, temos:
- 11. As razões trigonométricas de 30º, 45º e 60º Resumindo: x sen x cos x tg x 30º 45º 60º
- 12. Exercícios resolvidos: 01. (UEPA – PRISE) O mastro (CD) de um navio é preso verticalmente por cabos de aço fixo na proa (A) e na popa (B), conforme mostra a figura a seguir. Se o cabo BC mede 10 3 m então, a altura do mastro é:
- 13. Resolução: Destacamos o triângulo BCD retângulo em D: ___ A razão trigonométrica a ser aplicada é o seno, pois o mastro (CD) é o cateto __ oposto ao ângulo de 30º e o cabo (BC) é a hipotenusa. Sen30º = , = e como sen30º = 1/2 , temos: • Portanto a altura do mastro é (alternativa b).
- 14. 02. (UEPA – PRISE) Um botânico interessado em descobrir qual o comprimento da copa de uma árvore fez as observações indicadas na figura abaixo a partir de um ponto no solo. O comprimento (H), em metros, dessa copa é:
- 15. Resolução: Observe o esquema: Destacamos os dois triângulos retângulos a seguir:
- 16. Triângulo 1: Observe que x representa a medida do tronco da árvore e para calcular este valor aplicamos a tangente de 45º, pois x é o cateto oposto e 10 m é a medida do cateto adjacente.
- 17. Triângulo 2: Observe que y representa a altura da árvore e para calcular este valor aplicamos a tangente de 60O, pois y é o cateto oposto e a medida 10 m é o cateto adjacente. Substituindo x e y na relação H + x = y , temos: Portanto o comprimento da copa da árvore é
