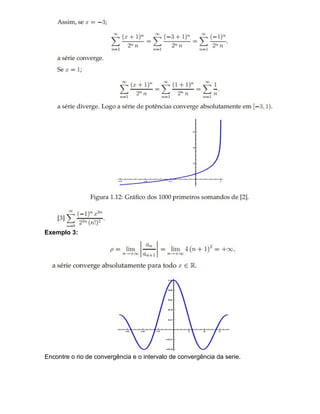
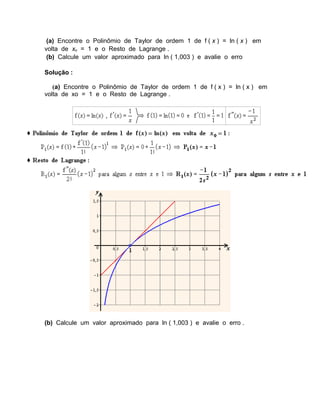
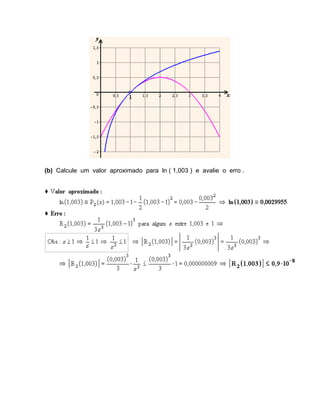
O documento discute séries de potências e séries de Taylor. Séries de potências dependem de um parâmetro e convergem dependendo da distância desse parâmetro de um ponto no plano complexo. Séries de Taylor aproximam funções através de polinômios gerados pelas derivadas da função em um ponto. O documento fornece exemplos e fórmulas para calcular raios de convergência, polinômios de Taylor e restos.

1. Séries de Potência
Definição: Uma série de potências é uma série que depende de um parâmetro ,
da seguinte forma:
o número , a sequência e o parâmetro podem ser em geral números
complexos. 1
A convergência da série de potências depende da distância entre e no plano
complexo:
Convergência: da série de potências ao conjunto dos valores reais que,
substituídos na série, originam uma série numérica convergente. Uma série de
potências é uma função, que está definida no seu domínio de convergência.
O valor 0 pertence sempre ao domínio de convergência da série.
Raio de convergência: Se a distância for suficientemente aproximada a zero, a
série converge ( o valor da série quando ); quanto maior for a distância
mais lenta será a convergência, até que a partir de uma certa distância a série
diverge. O valor máximo da distância para o qual a série converge, é o
chamado raio de convergência ( ) e calcula-se a partir de:

2. Exemplo 1:
Exemplo 2:

3. Exemplo 3:
Encontre o rio de convergência e o intervalo de convergência da serie.

4. Séries de Taylor
Exemplo 4:
Exemplo 5:
Em matemática, a série de Taylor ou série de potências é uma série de funções da
seguinte forma:

5. A constante é o centro da série que pode ser encarada como uma função real
ou complexa. Se a= 0, a série também é chamada de Série de Maclaurin (de Colin
Maclaurin).
Série de Taylor associada a uma função
A série de Taylor associada a uma função f infinitamente diferenciável (real
ou complexa) definida em um intervalo aberto (a − r, a + r) é a série de potências
dada por
Onde, n! é o fatorial de n e f (n)(a) denota a n-ésima derivada de f no ponto a.
Com essa ferramenta, podem ser moldadas funções trigonométricas, exponenciais
e logarítmicas em polinômios.
Lista de série de Taylor de algumas funções comuns
1- Função exponencial e logaritmo natural:
2- Série geométrica:
3- Teorema binomial:
4- Funções trigonométricas:
onde Bs são números de Bernoulli.

6. 5- Funções hiperbólicas:
6- Função W de Lambert:
Definição – Polinômio de Taylor de Ordem n
Seja f uma função com derivadas de ordem k para k = 1, 2, ..., N em algum
intervalo contendo a como um ponto interior. Então, para algum inteiro n de 0 a N,
o polinômio de Taylor de ordem n gerado por f em x = a é o polinômio
P x = f a + f a x - a + f a x -a + + f a - + + -
( ) .
n
x a f a
( ) ... ( )
!
( ) ... ( )
!
( ) ( ) ´( )( ) ´´( )
2!
( ) ( )
2 k
n
k
n x a
n
k
Resto de um Polinômio de Taylor
Precisamos de uma medida da precisão na aproximação do valor de uma função
f(x) por seu polinômio de Taylor Pn(x). Podemos usar a idéia de um resto Rn(x)
definido por

7. f (x) P (x) R (x) n n = +
O valor absoluto R (x) f (x) P (x) n n = - é chamado de erro associado à
aproximação.
Teorema de Taylor
Se f for derivável até a ordem n + 1 em um intervalo aberto I contendo a, então
para cada x em I existe um número c entre x e a tal que
f ( x ) f ( a ) f ´( a )( x a ) f ´´( a ) x a f a ( )
n
( ) ( ),
( ) ... ( )
!
2!
( )
2 x a R x
n
n
n
= + - + - + + - +
onde
( 1)
R x f c
( ) = ( ) n
1
( ) .
( 1)
+
+
-
+
n
n x a
n
Teorema da Estimativa do Resto
Se existirem constantes positivas M e r tais que f (n+1) (t) £Mr n+1 para todo t
entre a e x, inclusive, então o resto Rn(x) no Teorema de Taylor satisfará a
desigualdade
.
-
( 1)!
( )
1 1
+
£
+ +
n
r x a
R x M
n n
n
Se essas condições forem válidas para todo n e todas as outras condições do
Teorema de Taylor forem satisfeitas por f, então a série convergirá para f(x).
Combinando Séries de Taylor
Na interseção dos seus intervalos de convergência, as séries de Taylor podem ser
somadas, subtraídas e multiplicadas por constantes e potências de x, e os
resultados são novamente séries de Taylor. A série de Taylor para f(x) + g(x) é a
soma da série de Taylor para f(x) e a série de Taylor para g(x) porque a enésima
derivada de f + g é f(n) + g(n) e assim por diante.
Exemplos 1:

8. (a) Encontre o Polinômio de Taylor de ordem 1 de f ( x ) = ln ( x ) em
volta de xo = 1 e o Resto de Lagrange .
(b) Calcule um valor aproximado para ln ( 1,003 ) e avalie o erro
Solução :
(a) Encontre o Polinômio de Taylor de ordem 1 de f ( x ) = ln ( x ) em
volta de xo = 1 e o Resto de Lagrange .
(b) Calcule um valor aproximado para ln ( 1,003 ) e avalie o erro .

9. Exemplo 2:
(a) Encontre o Polinômio de Taylor de ordem 2 de f ( x ) = ln ( x ) em
volta de xo = 1 e o Resto de Lagrange .
(b) Calcule um valor aproximado para ln ( 1,003 ) e avalie o erro .
Solução :
(a) Encontre o Polinômio de Taylor de ordem 2 de f ( x ) = ln ( x ) em
volta de xo = 1 e o Resto de Lagrange .

10. (b) Calcule um valor aproximado para ln ( 1,003 ) e avalie o erro .