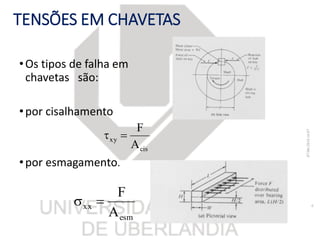
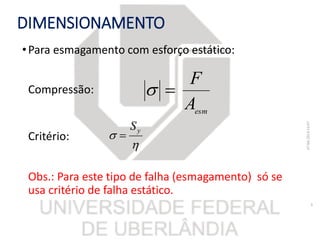
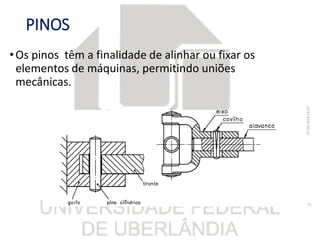
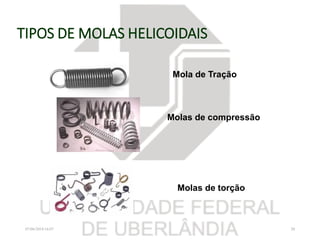
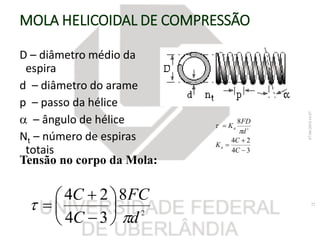
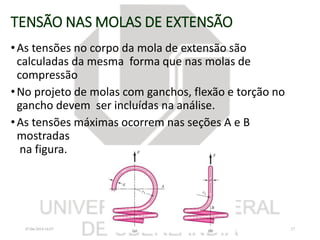
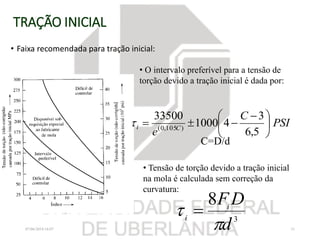
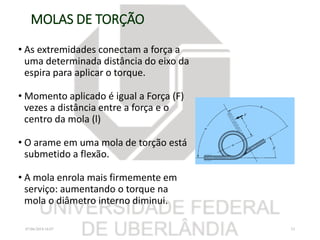
O documento resume os principais tópicos sobre chavetas, pinos, eixos e molas mecânicas. Detalha os tipos de chavetas e como dimensioná-las para resistir a cisalhamento e esmagamento. Também descreve os tipos de eixos, como projetá-los considerando deflexão, resistência e velocidade crítica, e dimensionar pinos. Por fim, explica os tipos de molas helicoidais e como calcular sua constante e tensões.