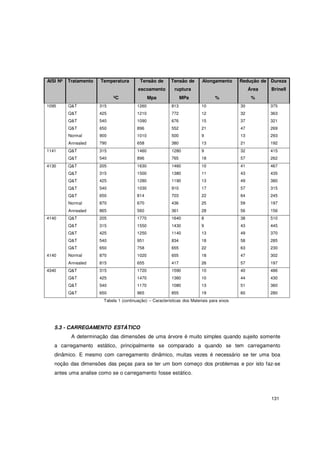
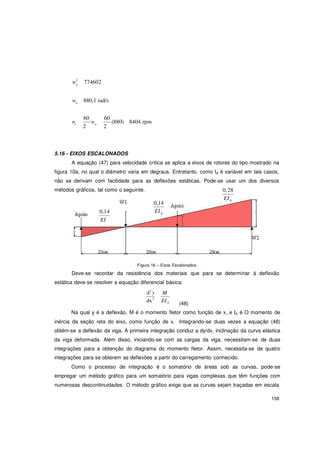
O documento discute eixos e árvores de transmissão. Apresenta fórmulas para calcular tensões em eixos sujeitos a flexão, torção e esforço axial estático. Fornece exemplos de materiais usados e características mecânicas. Resolve exercícios aplicando as fórmulas para dimensionar eixos sob carregamento estático de flexão e torção.

1. 129
CAPITULO 05 - EIXOS E ARVORES DE TRANSMISSÃO
5.1 - INTRODUÇÃO
Eixo é um elemento mecânico rotativo ou estacionário (condição estática) de secção
usualmente circular onde são montados outros elementos mecânicos de transmissão tais como:
engrenagens, polias, ventiladores, rodas centradas, entre outros. Os eixos são suportados
(apoiados) em mancais, de deslizamento ou rolamento, tendo secção quase sempre mássica e
variável, com rasgos de chavetas para fixação de componentes. A figura 1 mostra uma
iluminação de um eixo.
Figura 1 – Eixo
Os eixos são elementos solicitados a esforços de flexão, tração/compressão ou torção,
que atuam individualmente de forma combinada. Para a segurança do sistema em que o eixo
está inserido, este deve ser dimensionado para cargas estáticas (parado ou com rotação muito
baixa) ou dinâmica (altas rotações). Este dimensionamento leva em conta a resistência do
material de que foi confeccionado, comparam-se as tensões que atuam no mesmo com os
limites de resistência do material, estáticos (Sy ou Su) ou dinâmicos (Se – fadiga).
Em certos sistemas mecânicos, o nível de deflexão do eixo pode constituir em um
parâmetro crítico, devendo o eixo ser dimensionado usando a teoria de deflexão. Em outras
palavras, a geometria do eixo deve ser definida para os limites aceitáveis de deflexão, antes da
análise das tensões/resistências.
5.2 - MATERIAIS PARA EIXOS E ÁRVORES
Há uma grande variedade de materiais possíveis para a fabricação de eixos e árvores.
De acordo com o serviço devem ter alta resistência e baixa sensibilidade aos efeitos da
concentração de tenção.
Para se obter, em um cálculo, diâmetros menores e grandes resistências, pode-se usar
aços-liga, em geral tratados termicamente. Estes aços, porém têm a desvantagem de serem

2. 130
caros e de maior sensibilidade às concentrações de tensões. Além disso, o diâmetro é muitas
vezes subordinado à certas deformações admissíveis, tornando o aço-liga contra indicado, já
que o problema não é mais de resistência.
Os aços-carbono, de baixo e médio teor, são, muito usados na fabricação de eixos e
árvores. Aços muito empregados são os seguintes: SAE 1015, 1020, 1025, 1030, 1040, 1045,
2340, 2345, 3115, 3120, 3135, 3140, 4023, 4063, 4140, 4340, 4615, 4620 e 5140.
Como vemos uma grande variedade de material existe para a confecção de eixos e
árvores. A seleção dependerá sempre das condições de serviço, custo, usinabilidade e
características especiais por ventura exigidas. É um campo muito aberto em que o projetista
deve procurar sempre maiores conhecimentos, pois praticamente qualquer material ferroso,
não-ferroso ou não metálico, pode ser usado, por uma razão qualquer, na execução de um eixo
ou uma árvore.
AISI Nº Tratamento Temperatura
ºC
Tensão de
escoamento
Mpa
Tensão de
ruptura
MPa
Alongamento
%
Redução de
Área
%
Dureza
Brinell
1030 Q&T
Q&T
Q&T
Q&T
Q&T
Normal
Annealed
Q&T
Q&T
205
315
425
540
650
925
870
205
425
848
800
731
669
586
521
430
779
758
648 17
621 19
579 23
517 28
441 32
345 32
317 35
593 19
552 21
47 495
53 401
60 302
65 255
70 207
61 149
64 137
48 262
54 241
1040
1050
Q&T
Normal
Annealed
Q&T
Q&T
Q&T
Normal
Annealed
650
900
790
205
425
650
900
790
634
590
519
1120
1090
717
748
636
434 29
374 28
353 30
807 9
793 13
538 28
427 20
365 24
65 192
55 170
57 149
27 514
36 444
65 235
39 217
40 187
1060 Q&T
Q&T
Q&T
Normal
Annealed
425
540
650
900
790
1080
965
800
776
626
765 14
669 17
524 23
421 18
372 22
41 311
45 277
54 229
37 229
38 179
Tabela 1 – Características dos Materiais para eixos

3. 131
AISI Nº Tratamento Temperatura
ºC
Tensão de
escoamento
Mpa
Tensão de
ruptura
MPa
Alongamento
%
Redução de
Área
%
Dureza
Brinell
1095 Q&T
Q&T
Q&T
Q&T
Normal
Annealed
1141 Q&T
Q&T
4130 Q&T
Q&T
Q&T
Q&T
Q&T
Normal
Annealed
315
425
540
650
900
790
315
540
205
315
425
540
650
870
865
1260
1210
1090
896
1010
658
1460
896
1630
1500
1280
1030
814
670
560
813 10
772 12
676 15
552 21
500 9
380 13
1280 9
765 18
1460 10
1380 11
1190 13
910 17
703 22
436 25
361 28
30 375
32 363
37 321
47 269
13 293
21 192
32 415
57 262
41 467
43 435
49 380
57 315
64 245
59 197
56 156
4140
4140
Q&T
Q&T
Q&T
Q&T
Q&T
Normal
Annealed
205
315
425
540
650
870
815
1770
1550
1250
951
758
1020
655
1640 8
1430 9
1140 13
834 18
655 22
655 18
417 26
38 510
43 445
49 370
58 285
63 230
47 302
57 197
4340 Q&T
Q&T
Q&T
Q&T
315
425
540
650
1720
1470
1170
965
1590 10
1360 10
1080 13
855 19
40 486
44 430
51 360
60 280
Tabela 1 (continuação) – Características dos Materiais para eixos
5.3 - CARREGAMENTO ESTÁTICO
A determinação das dimensões de uma árvore é muito simples quando sujeito somente
a carregamento estático, principalmente se comparado a quando se tem carregamento
dinâmico. E mesmo com carregamento dinâmico, muitas vezes é necessário se ter uma boa
noção das dimensões das peças para se ter um bom começo dos problemas e por isto faz-se
antes uma analise como se o carregamento fosse estático.

4. 132

2
 2
2
xy
' 3
5.3.1 - CARREGAMENTO ESTÁTICO SUJEITO À FLEXÃO, TORÇÃO E ESFORÇO AXIAL
As tensões em um ponto na superfície de uma árvore de diâmetro (d) sujeita flexão,
torção e carregamento axial são:
32 M 4 F 16 T
x (1) (2)
d 3
d 2 xy
d 3
Onde a componente axial (F) de σx pode ser positiva ou negativa. Nós observamos que
há três carregamentos. Momento (M), força (F), e torque (T) aparecem na seção contendo o
ponto especifico na superfície.
Usando o circulo de Mohr podemos mostrar que as 2 principais tensões não nulas, são:
1
 x  2
a b x  
 2 
xy 

(3)
Estas tensões podem ser combinadas de forma a obter a máxima tensão de
cisalhamento (τmax) e a tensão de Von Mises (σ’); dando em:
1
   2
a b
 x

2
 (4)max
2   2  
1
2 2 2
a a b b
1
2 2 2
x xy (5)
Substituindo as equações (1) e (2) em (4) e (5) teremos:
 2 
1
2 2 2 (6)max 
 d 3  8 M F D 8 T
'
4
8 M
d 3
F d
2
1
48 T 2 2 (7)
Estas equações nos permitem determinar τmax ou σ’ quando o diâmetro(d) é dado ou
determinar o diâmetro quando tivermos posse das tensões.
Se a analise ou projeto da árvore for baseada na teoria da máxima tensão de
cisalhamento, então τmax é:
all
SSy Sy
n 2 n
(8)
As equações (6) e (8) são úteis para a determinação do fator de segurança(n), se o
diâmetro for conhecido, ou para determinar o diâmetro se o coeficiente de segurança for
conhecido.

5. 133
'
y
y
Uma analise similar pode ser feita levando em conta a teoria da energia de distorção
para falhas, onde a tensão de Von Mises é:
S y
'all
n
(9)
5.3.2 - CARREGAMENTO ESTÁTICO SUJEITO À FLEXÃO E TORÇÃO
Em varias aplicações, a componente axial (F) das equações (6) e (7) é próxima de zero
ou tão pequena em relação às outras que pode ser desconsiderada. Daí teremos:
max
16
d 3
16 
(M 2
1
T 2
)2
2 2
1

(10)
3  4 M
d 
3 T 2


(11)
É mais fácil resolver estas equações para se encontrar o diâmetro. Substituindo as
equações (8) e (9) nos temos:
 32 n
d 
 Sy
M 2
T 2
1
1  3
2


(12)
Usando a teoria de máxima tensão de cisalhamento, se o diâmetro for conhecido,
calcula-se n da seguinte forma:
1 32
n d 3
S
1
M 2
T 2
2 (13)
Se usarmos como base a teoria de energia de distorção, teremos:
16 n
d 
 Sy
4 M 2
3
1
1 3
T 2 2


(14)
Onde:
1 16
4 M 2
n d 3
S
1
3 T 2 2 (15)
n = fator de segurança. n = 1,5 a 2,0
Sy = limite de escoamento do material.
M = momento Máximo no eixo.
T = torque máximo.

6. 134
5.4 – EXERCÍCIOS RESOLVIDOS - CARREGAMENTO ESTÁTICO SUJEITO À FLEXÃO E
TORÇÃO
1. Qual o diâmetro de um eixo mostrado na figura 2, feito de um aço AISI 1035 laminado
F 700N
3,73kW
Figura 2 – Engrenagem no eixo.
Motor
n
I) Torque:
1750rpm
T
30 103
.H
.n , onde H=> Potência em KW, tem-se:
T
30 103.3,73
.1750
T 20,35N.m
II) Momento:
M
F
.
L 700
.
0,3
2 2 2 2
M 52,5N.m
III) Material:
Pela Tabela =>
IV) Segurança:
Usar n=2.
V) Diâmetro:
Sy 462MPa

7. 135





2
3

 
y
  
1
d
 32n
M 2
T
1
2
 .Sy
d
 32.2


52,52
1
1 3
20,352 2

.462 106 
d 13,54mm
2. Do exercício anterior visto, tem-se:
M 52,5N.m 
T 20,35N.m

S 462MPa
d 13,47mm
n 2 

M 52,5N.m
T 20,35N.m
Sy 462MPa
Su 551,5MPa
Ka 0,78
Kb 0,85
Kc 0,923(Su
Kd 1,0
Ke 1,0
Kf 1,0
Se
1520MPa)
Ka.Kb.Kc.K d.Ke.Kf.Se '
Se (0,78)(0,85)(0,923)(1)(1)(1)(0,504.551,5
Se 170,1MPa
106
)


2
1
1  3
2  2
d
32.2

52,5   20,35 


 
 170,1



106


 551,5
 
106



d 18,50mm
5.5 - DIMENSIONANDO EIXOS PELA NORMA ASME
OBSERVAÇÃO: a norma ASME para Eixo de Transmissão:
- Não considera fadiga
- Não considera concentração de tensão

8. 136
m t
2
Segundo a norma ASME – as máximas tensões são cisalhantes:
d 0,30.S yt d 0,18.Sut (16)
d = máxima tensão cisalhante admissível
S yt
Su
tensão escoamento admissível
tensão de ruptura admissível
As normas prevêem que se as concentrações de tensões estiverem presentes devido a
entalhe em chavetas, a tensão máxima admissível deve ser diminuída de 25%. A máxima
tensão cisalhante em um eixo submetido à flexão-torção é dada por:
2
 
 a

2
(17)max
x
 2
M
.y
I
xy

M
.
d
.d
4
2
32.M
.d 3
T
.y
64
M
.
d 16.T
x
I
logo,
.d
4
2
64
.d 3
1
.
32.M

16.T
 max x
  
4  .d3
 
16
M 2
T 2

.d 3

min
.d 3
x tensão de flexão (psi)
xy
tensão de torção (psi)
M momento de flexão (lbf.in)
T = momento de torção (lbf.in)
d = diâmetro dp eixo (in)
Segundo o critério da ASME, momento M e T devem ser multiplicados por fatores de
correção devido a choques e fadiga.
16.T
. M 2
T 2
d
.d 3
→
16.T
.d
.d 3
C .M 2
C T 2
→ Fórmula da ASME (19)

9. 137
para diâmetro de eixos baseado na teoria da máxima tensão cisalhante. Fatores Cm e Ct dados
na tabela.
5.6 - EIXOS E ÁRVORES SUJEITOS À FADIGA
Qualquer árvore girante que sofre momento de flexão e torção fixas estão sujeitos a uma
inversão, reversão completa da tensão causada pelo giro da árvore, mais a tensão de
cisalhamento permanecerá a mesma.
onde:
32 M a
xa
d 3
(20) xym
16 Tm
d 3
(21)
σxa = Tensão de Amplitude Alternada
τxym = Tensão de Cisalhamento Constante
Estas duas tensões podem ser manipuladas usando dois círculos de Mohr
Se estivermos usando a teoria de máxima tenção de cisalhamento, teremos:
a 2 a (22) m 2 m (23)
Se estivermos usando a teoria da energia de distorção, teremos:
a xa (24) m 3 xym (25)
5.6.1 - CRITÉRIO DE FADIGA – GOODMAN
Para qualquer eixo carregado com um momento de flexão e torção fixos, estará
submetido a uma flexão reversa provocando tensões alternadas e torção estacionária,
provocando tensões médias. Assim tem-se:
32Ma
ax
d3 mxy
16Tm
d3 (26)
Usando estas expressões e a equação da linha de Goodman:
a
Se
m
1
Su
(27)
Pode-se obter, após desenvolvimento analítico que:

10. 138

T


2


32n  M 
2
T  
1
1
2  3

d   a
  m
   (28)
  Se 

 Su  

5.6.2 – CRITÉRIO DE FADIGA - SODERBERG
Utilizando o teorema da máxima tensão cisalhante:
16.T
xy
.d 3
32.M
x
.d 3
Para qualquer plano fazendo um ângulo α com o plano horizontal tem:
16.T
.cos 2.m
.d 3
→ valor médio
16.M
.sen2.a
.d 3
→ (amplitude da componente alternativa)
Por meio da geometria analítica, tem-se que:
.d 3
n (29)
16.
2
 
 
 
2
 M 
 
 Ssy   Sse 
 2
 
1
1
3
2  2
16.n T
d . 
 M 


(30)
  
  
  Ssy 

 Sse   

Para o critério da máxima tensão cisalhante (usada)
 2
 
1
1
3
2  2
32.n T
. 
 M 


d   
   (31)
sendo que: Ssx 0,5.Sx
  Sy 

 Se   

n Fator de segurança.
S y Tensão de escoamento.
Se Limite de resistência à fadiga.

11. 139
Para casos mais gerais usar equação:

12. 140
2

2

 e  S S S 

n  T 
2 2
 M   M   M
1
1
3
 2
32.
d 
. a
  m   a
  am  

(32)
onde:
 S 
 
 
 y 
 
 e 
 
 y   
Ta
Tm
M a
M am
Torque (amplitude)
Torque médio
Momento (amplitude)
Momento médio
5.7 – EXERCÍCIOS RESOLVIDOS - CRITÉRIO DE FADIGA POR SODERBERG
1. Um eixo usinado é fabricado de um aço com Su = 550 MPa. Calcular n.
Dado: T = 6,0 KN
R
175.F
1
500
R
325.F
1
500
a tensão alternada
max min
=a
2
n
Se
a
max
M
a
I
c
M R1.L
100Mpa
175.F
.200
500
420KN.m
.d 4
I
I onde:
64 c
.d3
d
e c
32 2
M
a KF .
I
c
Se
Se´
Ka .Kb .Kc .Kd .Ke .Se ´
0,504.Su

13. 140
b
a
Ka a.Su a = 4,51 e b = -0,265
K 4,51.550 0,265
0,847
 d
Kb 
0,1133

 0,841
 7,62
Kc Kd 1
K
1
e
K f
K
r
0,0857f
d
→ K t 1,72 → D
1,428
d
K f 1 q. Kt 1) 1,58 q 0,80
logo, Ke
logo,
1
1,58
0,633
Se 124,4MPa
n
Se
a
124,4
99,08
1,25
2. A transmissão representada na figura é movida por um motor elétrico, assíncrono, de
indução, trifásico, com potência P= 3,7 kW e rotação n= 1140 rpm. Dimensionar o
diâmetro da árvore 2, sabendo-se que a árvore é maciça e o material utilizado possui Su
= 700 Mpa, Sy = 630 Mpa e o fator de projeto é 1,8, com as engrenagens enchavetadas
no eixo (adotar Kf= 2,8). As engrenagens são cilíndricas (ECDR) e possuem as
seguintes características geométricas:
Z1= 23; Z2=49; Z3=28 e Z4= 47 m= 2,5 mm e ângulo de pressão 20º.

14. 141
F
T
0
0
0 2
0 3
Figura 3 - Exercício resolvido 1.
Calculemos o torque na árvore 1
3000 P Z2
MT 2
. .
n Z1
A potência do motor - P = 3700 W
Portanto
3000
.
3700
.
49
MT 2
1140 23
MT 2
66.030N.mm
Esforços na transmissão:
Força tangencial (FT)
Força tangencial (no primeiro par)
Diâmetro primitivo
2.M 2
T
d 2
d m.Z2
2,5.49 d02
122,5mm
F
2x66030
T
122,5
FT 1.078N
Diâmetro primitivo:
d m.Z3
2,5.28 d 70mm3
F
2x66030
T
70
FT 1.887N
Força radial no primeiro par
FR FT .tg20º
FR 1078.tg 20º FR 392N

15. 142
Força radial no segundo par
FR FT .tg20º
FR 1887.tg20º FR 687N
Momento fletor
Plano vertical
M A 0
600.RBV
687.500 392.100
RBV
638N
Figura 4 – Forças cisalhantes, diagrama de
momento fletor no plano vertical
Fy
RAV
RAV
0
RBV
441N
392 687
M max RAV .500 392.400
M max 63.700N.mm

16. 143
S
S S
'
e e
Plano Horizontal
M A 0
600.RB H
RB H
1078.100
1393N
1887.500
Fy
RA H
RA H
0
RBH
584N
1087 1887
2 2
M max M H MV
M max 637002
1393002
Figura 5 – Forças cisalhantes, diagrama de
momento fletor no plano horizontal
M max 153.174N.mm
Cálculo do diâmetro considerando cargas estáticas
TMTC
32.n
d  .(M 2
1
1
3
T 2
)2

 .Sy 
32.1,8
d  .(1531742
1
1
3
660302
)2
 d 16,95mm

TED
.630 
16.n
d  .(4.M 2
1
1
3
3.T 2
)2
 d 16,99mm
 .Sy 
Cálculo do diâmetro considerando carregamento dinâmico
e 0,504.Su
'
0,504.700
'
352,8Mpa

17. 144
e
2
b
a
1
2
Ka a.Su a = 4,51 e b = -0,265
K 4,51.700 0,265
0,784
 d
Kb 
0,1133


 7,62
0,1133
 
K 
16,93
b
 7,62 
0,91
Kc Kd 1
K
1
e
K f
K f 2,8 Ke 0,357
Se Ka .Kb.Kc.Kd .Ke.S '
Se 0,784x0,91x1x1x0,357x352,8
Cálculo do diâmetro pelo critério de Goodman
1

 2 2
3
d
32.n
.
 Ma

Tm   
      
  Se 

 Su  


32.1,8 155215,3 
2
1
1
3
 66030   2

d  .
 


84,86 

 700
  
  

d 32,15mm
5.8 – CHAVETAS / PINOS
Chavetas e pinos são dispositivos mecânicos usados para fixar no eixo, engrenagens,
polias e outros elementos de tal forma que o torque possa ser transmitido através dele. Os
pinos são usados com duplo propósito, o de transmitir o torque e evitar deslocamento axial do
componente montado no eixo. A figura abaixo ilustra estes dispositivos.

18. 145
Figura 6 – Chavetas e Pinos.
5.9 - UNIÃO DE EIXOS COM CUBOS
O cubo é a parte centra do elemento (polia, engrenagem, etc.) onde é realizado um
rasgo para a fixação da chaveta.
Figura 7 – União de eixos com chavetas cúbicas.
A chaveta é uma peça que vai ocupar o rasgo no eixo e no cubo, simultaneamente,
fazendo a união dos mesmos.
Os principais tipos de chavetas, as mais usadas são definidas por normas (padrões).
Estas chavetas são do tipo:
Chaveta meia-lua (woodruff)
Chaveta plana.
Chaveta inclinada.
A figura 8 mostra estas chavetas e a geometria, bem como a forma de usinagem do
rasgo. Observar que os rasgos das chavetas meia-lua são usinados com fresa circular as
chavetas planas e inclinadas com fresa circular e de topo.

19. 146
Para exemplificar os padrões de chavetas tem-se:
Uniões por adaptação de forma.
Uniões por adaptação de forma com pretensão.
Uniões por atrito.
Chaveta meia-lua.
Chavetas planas e inclinadas.
Figura 8 – Tipos de Chavetas
5.10 - DIMENSIONAMENTO DE CHAVETAS
Como já foi visto anteriormente, as chavetas são tabeladas quanto a sua secção.O
dimensionamento da chaveta consiste em determinar o seu comprimento mínimo (L), como é o
caso das chavetas planas e inclinadas (as mais usadas).

20. 147
Figura 9 – Dimensionamento das chavetas.
As tensões que atuam nas chavetas são determinadas da seguinte forma:
Figura 10 – Tensões atuantes nas chavetas.
Quando a chaveta acopla (une) um eixo e uma polia, a transmissão de potencia do eixo
para a polia, força a chaveta de forma inclinada. Esta força (F) tende a cisalhar (rasgar) a seção
AA’ da chaveta. Logo:
F F
A t.L Modelo Matemático (33)
Comparando com o limite de resistência cisalhante ao escoamento (Ssy) e para um fator
de segurança n, tem-se:
Ssy
n
F
t.L
Ssy
n
(34)
5.11 – EXERCÍCIOS RESOLVIDOS – CHAVETAS
1. Um eixo de aço AISI 1018 (ABNT) trefilado a frio tem Ssy = 185MPa. Uma chaveta
quadrada deve ser usada para acoplar um eixo de d = 40mm e uma engrenagem, que
transmitirão 22,38KW a uma rotação de 1100rpm. Usar fator de segurança n = 3,0.

21. 148
T
F
d => Força na chaveta
2
R
d 40
⇒ R
2 2
20mm
Como: T
30 103
.H
.n
, onde H=> Potência em KW, tem-se
T
30 103
.22,38
⇒ T
.1100
Figura 11 – aplicação de chaveta.
194,2N.m
Logo:
F
194,2
⇒ F 9713N
20 10 3
Para a chaveta, temos:
F
t.L
Ssy
n
L
F
.
t.
n
Ssy
L
9713
.
0,008 185
3
106
L 19,7mm
Observar que, o comprimento mínimo é L = 19,7mm como a geometria do cubo é
maior do que o diâmetro do eixo, e como as chavetas têm o comprimento do cubo,
pode-se dizer que o comprimento da chaveta a ser usada é:
L 40mm

22. 149
5.12 - VIBRAÇÃO DE EIXOS
A figura 12 mostra um rotor consistindo de um grande disco de massa M montado em
um eixo, na metade da distância entre os mancais. A massa do eixo será considerada
desprezível comparada com M. Mesmo com um balanceamento de alto grau de precisão, há
contudo uma pequena excentricidade e do centro de massa g do disco, em relação ao eixo de
rotação. Por causa da excentricidade, a força centrífuga ocasionada pela rotação do eixo faz
com que este sofra uma deflexão r. Visto pela extremidade do eixo como na figura 12, o centro
O do disco parece estar girando em torno do eixo de rotação sobre uma circunferência de raio r.
A força de inércia causada por este movimento forçado é Fo = M(r + e) w2
. Devido à deflexão do
eixo, considerado como uma mola, a resistência à força de inércia é kr, sendo k a constante de
mola do eixo na flexão. O sentido da aceleração do centro de gravidade g é conhecido neste
caso, de modo que se pode mostrar o vetor MA como uma força de inércia Fo (como na figura
12). Pode-se então escrever a equação do equilíbrio estático:
∑ F 0
M ( r e ) w 2
kr 0 (35)
Figura 12 - Rotor com disco

23. 150
n
n
Para se determinar o raio r, pode-se apresentar a equação (35) da seguinte forma:
ew 2
r
k w 2
M (36)
Quando a velocidade ω do eixo for igual a k / M , o denominador da equação (36) se
anulará e r atingirá valores intoleravelmente grandes. A rotação do eixo assim defletido parece
com uma viga em vibração quando visto do lado onde somente pode-se observar a projeção do
movimento. Portanto, pode-se considerar k / M do eixo rotativo como a freqüência circular
natural ωn da viga quando levada a vibrar naturalmente no seu primeiro modo de vibração.
Pode-se escrever a equação (36), na forma adimensional:
r (w/ w )2
e 1 (w/ w )2
(37)
A representação gráfica da equação (37) e indica a condição crítica de rotação, quando
ω for igual a ω n = k / M , devido às amplitudes muito grandes da vibração do eixo. Na
condição crítica, chama-se ω de ωc e a velocidade de rotação do eixo em rotações por minuto
será
60 60
nc
2
wc
2
wn
(38)
onde ω n = k / M normalmente é expresso em rad/s. Assim,
n
60
w
60 k
9,55
k
9,55
kg
29,9
k k
30c
2
n
2 M M P P P (39)
na qual nc è a velocidade crítica em rotação por minuto, k está em Newtons por metro e M. em
quilogramas. Pode-se calcular a constante k da mola através da deflexão estática δest do eixo
devido ao peso do rotor. Assim, k = Mg/δest e quando substituído na equação (39), a velocidade
crítica será expressa pela seguinte equação:
nc 30
1
est
(40)
Segundo os livros-texto de resistência dos materiais, pode-se calcular a deflexão
estática de uma carga P atuando no centro de uma viga uniforme bi-apoiada, como δest = Pl3
/48
EIA. Assim, a velocidade crítica de um eixo com uma massa M situado no meio da viga, pode
ser calculada em termos das dimensões do eixo (l é o comprimento do eixo, entre apoios, IA é o

24. 151
momento de inércia da área da seção reta do eixo, igual a πd4
/64, d é o diâmetro do eixo) e do
módulo de elasticidade E do material do eixo.
Ed4
nc 46
Pl3
(41)
Assim, de acordo com a equação (41), pode-se alterar o material e as dimensões do
eixo, assim como o peso da massa Af, de modo que a velocidade crítica nc seja superior ou
inferior à velocidade de projeto n na qual deseja-se operar. Caso n/nc for menor do que 0,707
ou maior do que 1,414, r será menor do que o dobro da excentricidade e. Por exemplo, se a
excentricidade e for 0,025 mm, r será 0,050 mm quando n/nc = 2 .
É interessante observar que em velocidades muito acima da crítica (ω/ωn>>1,0), o valor
de r/e = -1 e r = - e, indicando que o centro de massa de M estará no eixo de rotação. Neste
caso a massa não estará oscilando, porém o eixo oscilará em torno do centro de massa de M.
Até agora, considerou-se desprezível a massa do eixo. No caso da massa do eixo ser
grande bastante para não ser desprezada, e o eixo ter diâmetro uniforme, deve-se somar à
massa M 50 por cento da massa m do eixo, para se determinar à freqüência circular natural.
w
k
n
(M 0,5m) (42)
Conforme mostra a figura 12, supõe-se que os mancais do eixo sejam rígidos. Em certos
casos, pode-se considerar os mancais como elasticamente apoiados, e neste caso o δest da
equação (40) deve incluir a deflexão estática dos apoios assim como a deflexão do eixo.
Entretanto, aplica-se a equação (40) somente quando a flexibilidade dos apoios for a mesma
para todas as posições angulares do rotor.
5.13 - FREQÜÊNCIA NATURAL E VELOCIDADE CRÍTICA
Pode-se ter uma variedade muito grande de configurações de rotores desde que sejam
usadas diversas massas e diversos apoios, assim como eixos de diâmetros variáveis. Embora
as curvas do fator de amplificação sejam difíceis de serem obtidas matematicamente, as
velocidades críticas dos eixos são determinadas com relativa facilidade através de cálculos de
freqüência natural. No próximo item, serão apresentados diversos casos de determinação da
velocidade crítica a partir da freqüência natural.

25. 152
5.14 - FREQÜÊNCIA NATURAL DE EIXOS COM DIVERSAS MASSAS
Em um eixo rotativo com diversas massas conforme mostra a figura 13a, pode-se
determinar a freqüência circular natural ωn do eixo que, sem girar, vibra livremente, sem
amortecimento, após uma deflexão inicial no primeiro modo de vibração.
Pode-se aplicar o método de Rayleigh neste caso. Considerando que o sistema
vibratório é conservativo, a soma da energia potencial e da cinética é constante em qualquer
fase da vibração. Duas destas fases analisam-se facilmente. Na fase em que todas as massas
estão simultaneamente nos máximos deslocamentos Y, a energia armazenada elasticamente
no eixo é igual è energia potencial ∑ FY/2. Nesta fase a energia cinética é zero porque todos os
pontos do sistema estão momentaneamente com velocidade zero. Assim, a energia potencial é
EP
F1Y1 F2Y2
...
FnYn
2 2 2 (43)
As forcas F são as necessárias para a deflexão do eixo, como se fosse uma mola, ate
ficar com a conformação mostrada nesta fase. O produto forca-deslocamento determina energia
potencial. Entretanto, como a forca e diretamente proporcional ao deslocamento, a forca media
que atua durante o deslocamento Y e F/2.
Durante a vibração, o eixo passa pela fase de repouso (não deformada) na qual a
energia potencial e zero, mas a energia cinética e máxima porque as velocidades das massas
são máximas. Considerando que as massas tem movimento harmônico simples, as velocidades
são V = Yωn e as energias cinéticas são MV2
/2 = M(Yωn)2
/2. Assim, a energia cinética do
sistema é
2 2
EC
wn
M Y 2
M Y 2
M Y 2

wn
PY 2
P Y 2
P Y 2
 1 1 2 2 ... n n   1 1 2 2 ... n n 2 2g
(a) Flexão dinâmica
(44)

26. 153
w 2
d1
d2
d3
n
W1 W2 W3
(b) Flexão estática
Figura 13 – Flexão
Igualando-se os membros da direita das equações (43) e (44), pode-se deter-minar a
freqüência circular natural ωn. Entretanto, as forças F e os deslocamentos Y não são
conhecidos, mas podem ser determinados considerando-se a forma do eixo defletido
estaticamente sob a ação dos pesos conforme indica a figura 13b. Considerando que os
deslocamentos Y da vibração são proporcionais as deflexões δ da deformação estática, então
Y1 Y2
...
Yn
1 2 n (45)
Como as formas para defletirem uma mola são proporcionais as deflexões então
F1 Y1
,
F2 Y2
,
Fn Yn
P1 1 P2 2 Pn n (46)
Igualando as expressões da energia potencial e da cinética dadas pelas equações (43) e
(44) e usando as equações (45) e (46) para a eliminação de F e Y, a equação resultante que da
a freqüência circular natural é
w2
g
P1 1 P2 2 ... Pn n
n
P 2
P 2
... P 2
 1 1 2 2 n n 
2
g
∑P
∑P
(47)
e a velocidade critica pode-se determinar de nc = 60 ωn /2π.
A equação de Rayleigh equação (47) e uma expressão simples e altamente útil para
determinar a freqüência natural fundamental de muitos tipos de rotores. A determinação da
deflexão estática constitui a maior parte do esforço necessário na execução dos cálculos
conforme está ilustrado nos exemplos seguintes. As fórmulas de deflexão de vigas, para
inúmeros casos, estão disponíveis em livros texto de resistência dos materiais e em manuais.
Pode-se aplicar o método da área do diagrama de momento fletor e outros em casos gerais.
Dispõe também de métodos gráficos, conforme ilustrado no item seguinte, para a determinação
das deflexões estáticas de rotores com eixos de diâmetros variáveis.

27. 154
Para inclusão da massa do eixo nos cálculos, deve-se dividi-lo em diversos
comprimentos, cada um tratado como se fosse uma massa adicional.
A equação (47) não e estritamente uma avaliação exata da freqüência natural porque a
curva das deflexões estáticas não e proporcional exatamente a curva deflexões dinâmicas,
como foi considerado. Entretanto, o resultado obtido equação e somente um ou dois por cento
superior a freqüência natural funda verdadeira. Considerando que outros fatores tais como
efeitos giroscópicos durante a oscilação, ajustagens forçadas de discos no eixo, e chavetas
alteram raramente a velocidade critica, a equação (47) produz uma resposta aceitável. A
deflexão dos apoios pode ter uma influencia maior sobre as velocidades críticas e devem ser
acrescidas as deflexões do eixo, na equação (47).
A freqüência natural dada pela equação (47) é a fundamental, ou a mais baixa
freqüência do sistema de massas. É desejável, portanto, se possível projetarem-se as
dimensões de um, eixo de tal modo que a velocidade crítica mais baixa seja superior à
velocidade de projeto. Entretanto, nem sempre isso é possível. Em turbinas de alta rotação, a
velocidade de operação pode estar entre duas velocidades críticas de modo que o eixo não
necessita tornar-se excessivamente pesado. Neste caso, é necessária a passagem pela
velocidade crítica mais baixa, o que pode ser perigoso. Entretanto, se o rotor estiver
cuidadosamente balanceado e a primeira velocidade crítica for baixa, as forças perturbadoras
serão pequenas nas regiões perto da crítica. Também, a amplitude de vibração à velocidade
crítica aumenta a níveis perigosos somente se for permitido um tempo para a amplitude crescer;
portanto, acelerando-se na passagem pela velocidade crítica, pode-se manter as amplitudes em
intensidades aceitáveis. O amortecimento natural do material do eixo, embora pequeno,
também tende a reduzir as amplitudes. Muitas máquinas bem sucedidas foram projetadas para
funcionar entre velocidades críticas.
Quando o eixo se estende para fora dos mancais como na figura 12a, deve-se inverter
os sentidos dos pesos como indica a figura 12b na determinação das deflexões estáticas para
emprego na equação (47). Deve-se notar que se simula dessa maneira a curva da deflexão
dinâmica de meia-onda, para obtenção da freqüência natural mais baixa.

28. 155
(a)
Figura 14 – Freqüência natural da estrutura
(b)
5.15 – EXERCÍCIOS RESOLVIDOS – VIBRAÇÕES EM EIXOS
1. Um rotor de compressor de 25 kg e um rotor de turbina, de 15 kg, são montadas em um
eixo de aço conforme mostra a figura 13a. O eixo deve operar à velocidade prevista de
10.000 rpm. Empregando a equação de Rayleigh (47) determine o diâmetro do eixo
mais leve que possa ser usado para que tenha uma velocidade critica fundamental de
12.000 rpm, com uma margem de segurança de 2.000 rpm.

29. 156
1 2
(a)
(b)
(c)
Figura 15 – Aplicação de vibrações em um eixo
(d)
Conforme a figura 15b mostra, inverte-se a carga P2 a fim de se obter uma curva de
deflexão com o formato do uma meia-onda simples. As figuras 15c e 15d mostram a
forma da viga deformada sob a ação de cada carga atuando independentemente,
conduzindo assim a dois casos cujas fórmulas deflexão estática mostradas a seguir
encontra-se em livros-texto de resistência dos materiais. Pelo método da superposição,
pode-se determinar as deflexões δ1 e δ2:
Pl3
P l2
a1 2
1 1 1
48EIA 16EIA
1 25 0,503
15 0,502
0,25 0,12369
 EIA  48 16  EIA
Pl2
a P a2
(l a) 0,322
2 2 2
16EIA 3EI A EIA
Usando-se a equação (47),

30. 157
A n
A
A

w2
g
P1 1 P2 2

gEI
 25 0,12369 15 0,332 
n 
P 2
P 2  A 25 0,123692
15 0,3322 
 1 1 2 2   
Para g= 9,81m/s² e E= 2,1 x 1010
kg/m²
w2
81,678 1010
In A
I 0,012243 10 10
w 2
Para nc= 12.000 rpm
w
2 nc
1260 rad/sn
60
Portanto, o momento de inércia necessário do eixo é:
I 0,012243 10 10
12602
Como IA= πd4
/64,
d4 64
I 395973, 4762 10-10
d 0,0793 m 79,9 mm
Deve-se usar um diâmetro de 80mm.
2. Os apoios do rotor do exemplo 1, figura 15a, foram considerados como rígidos.
Determine a velocidade crítica do rotor do exemplo 1 se cada um dos apoios sofrer uma
deflexão de 0,14/EIA sob um carregamento estático. Use IA = 1,84 x 10-6
m4
e E = 2,1 x
1010
kg/m2
.
Devido à flexibilidade dos apoios, as cargas Pl e P2 terão uma deflexão adicional.
Conforme indica a figura 16, sob o carregamento, o apoio da esquerda desloca-se para
baixo e o da esquerda para cima. Como se pode ver, não há influência nobre a deflexão
da carga P1, porém o deslocamento de Pl aumenta de 0,28/EIA. Portanto as deflexões
estáticas totais são
0,12369
1
0,332 0,28 0,612
2
EIA
EIA EIA EIA .
Substituindo estes valores na equação (47),

31. 158
n
w2
774602
wn 880,1 rad/s
n
60
w
60
(880) 8404 rpmc
2
n
2
5.16 - EIXOS ESCALONADOS
A equação (47) para velocidade crítica se aplica a eixos de rotores do tipo mostrado na
figura 10a, no qual o diâmetro varia em degraus. Entretanto, como IA é variável em tais casos,
não se derivam com facilidade para as deflexões estáticas. Pode-se usar um dos diversos
métodos gráficos, tal como o seguinte.
0,14
EI
0,14
EIA
0,28
EIA
Figura 16 – Eixos Escalonados
Deve-se recordar da resistência dos materiais que para se determinar à deflexão
estática deve-se resolver a equação diferencial básica:
d2
y M
dx2
EIA (48)
Na qual y é a deflexão, M é o momento fletor como função de x, e IA é O momento de
inércia da seção reta do eixo, como função de x. Integrando-se duas vezes a equação (48)
obtém-se a deflexão da viga. A primeira integração conduz a dy/dx, inclinação da curva elástica
da viga deformada. Além disso, iniciando-se com as cargas da viga, necessitam-se de duas
integrações para a obtenção do diagrama do momento fletor. Assim, necessita-se de quatro
integrações para se obterem as deflexões a partir do carregamento conhecido.
Como o processo de integração é o somatório de áreas sob as curvas, pode-se
empregar um método gráfico para um somatório para vigas complexas que têm funções com
numerosas descontinuidades. O método gráfico exige que as curvas sejam traçadas em escala

32. 159
a fim de que as áreas sob as curvas possam ser avaliadas através da medição de quadrados
ou usando-se um planímetro.
A figura 17a mostra um rotor de aço com uma engrenagem de 89,0 N e um eixo de três
diâmetros diferentes. Divide-se a viga em cinco partes, mostrando-se os pesos de cada parte
no respectivo centro de gravidade. Uma delas inclui o peso da engrenagem. A figura 17a é um
diagrama de carregamento a partir do qual pode-se determinar o diagrama de esforço cortante
mostrado na figura 17b através de métodos convencionais (a primeira integração). Obtém-se o
diagrama de momento fletor da figura 17c através das áreas do diagrama de esforço cortante (a
segunda integração). Por exemplo, a ordenada M1 é obtida a partir da área Al, a ordenada M2,
n
∑A
é a soma das áreas A1+A2 e a ordenada Mn é 1 . Deve-se levar em conta o sinal de cada
área. Devem-se multiplicar as áreas em milímetros quadrados pelo fator de conversão
apropriado obtido das escalas do diagrama de esforço cortante, afim de que as ordenadas do
diagrama de momento fletor sejam em N/mm.

33. 160
Figura 17 – Deflexões em um eixo de carregamento conhecido
Depois de realizadas as integrações, deve-se transformar o diagrama de momento fletor
no diagrama M/EIA conforme exigido pela equação (48). Divide-se cada ordenada do diagrama
de momento fletor pelo valor adequado de EIA (E = 207x x 103
N/mm2
para o aço e IA = πd4
/64)
para obtenção das ordenadas M/EIA da figura 17d. Obtém-se as ordenadas da figura 17 e
representando a inclinação dy/dx da elástica (terceira integração), através das áreas do
diagrama M/EIA. As ordenadas traçadas a partir do eixo x' são todas positivas. Entretanto, sabe-
se do formato esperado da elástica que as inclinações são negativas perto da extremidade da
esquerda da viga, positivas na extremidade da direita e nas proximidades do meio da viga há
uma inclinação nula. Assim, traça-se o eixo x escolhido arbitrariamente de tal modo que as

34. 161
w g
áreas negativas sejam aproximadamente iguais às positivas, na figura 17e. Faz-se a quarta
integração usando-se as áreas da figura 17e para obtenção das ordenadas da deflexão estática
y na figura 17f. Observa-se que as ordenadas da deflexão estática são negativas porque as
áreas da curva dy/dx são negativas na extremidade da esquerda onde se inicia a integração.
Embora estas ordenadas sejam levantadas a partir do eixo x traça-se o eixo x conforme
indicado porque se sabe que são nulas as deflexões da viga nos apoios. Como o eixo x, traçado
arbitrariamente no diagrama da inclinação da elástica figura 15e, havia dividido igualmente as
áreas negativas e positivas, então o eixo x' e o x da figura 15f deveriam coincidir.
Dos dados das curvas a e f, calculam-se os seguintes valores:
∑Py 2,94 N mm
∑Py
∑Py2
0,0385 mm
2
n
∑Py2
0,794 106
wn 865 rad/s
n
60(865)
c
2
8260 rpm
5.17 - VELOCIDADES CRÍTICAS DE ORDEM SUPERIOR
Para rotores que tem eixos de diâmetros variáveis como no item precedente, a
determinação da segunda velocidade critica e as velocidades de ordem superior quanto à
flexão, e relativamente mais complexa do que o cálculo da velocidade crítica fundamental da
equação (47). Os livros-texto de Timoshenko, Den Hartog e Thomson apresentam métodos
para rotores com tais eixos e para um número de rotores com eixos uniformes com e sem
massas concentradas. No casos de vigas uniformes simplesmente apoiadas e vigas uniformes
em balanço para as quais a formula seguinte calcula as diversas freqüências naturais:
wn Cn
EIA g
Pl3
(49)
E o coeficiente que indica a n-ésima freqüência natural, P e o peso total da viga em kg, e
/ e o comprimento da viga em metros. O eixo de transmissão do automóvel e eixo de bobina
são exemplos de vigas uniformes simplesmente apoiadas, e as palhetas de compressores e de
turbinas são exemplos aproximados de vigas uniformes em balanço.

35. 162
3
Consideremos o caso da palheta do rotor mostrada na figura 18. Mostra-se a palheta
como uma viga em balanço a qual sofre um ciclo de perturbação de flexão cada vez que passa
por uma palheta do estator e provoca uma mudança na força aerodinâmica. Se N e o número
de palhetas do estator, então a freqüência da perturbação em ciclos por minuto será o produto
de N pela rotação do rotor em rpm. Quando essa freqüência coincidir com a freqüência natural
fn da palheta devida à flexão, existira uma situação crítica. Para a palheta de aço mostrada na
figura 16, os cálculos seguintes ilustram a determinação das diversas velocidades criticas do
rotor para o caso de um estator de 30 palhetas.
E 207x103
N / mm2
g 9810mm / s2
I 76,2mm
I
bh 25,4x3,183
68,1mm4
A
12 12
p 76,5x10 6
N / mm3
P volume p (25, 4 76, 2 3,18)(76, 5 10 6
) 0, 471 N
w n1 c
EI Ag
1
Pl3
3,52
(207 103
) 68,1 9810
0, 471 76, 23
2870 rad/s
60w n1 60
2870 27, 400 ciclos/minfn1
2 2
Figura 18 – Encaixe palheta e rotor

36. 163
c
n
c
n
∑
n
n
f
A velocidade crítica do rotor ocorre gerando n1 Nnc1 .
n
fn1 27400
913 rpmc1
N 30
A segunda e a terceira velocidades críticas são
c2
c2 c1
1
c3
c3 c1
1
22,4
3,52
61,7
3,52
913 5810 rpm
913 16000 rpm
Em geral as palhetas de rotores devem ser delgadas e leves para maquinas de alta
rotação e freqüentemente ultrapassam a primeira e a segunda velocidades criticas. A seleção
do material e importante. Alguns materiais possuem propriedades de amortecimento melhores
do que outros, e isto pode significar a diferença entre o êxito e o fracasso em ultrapassar as
velocidades criticas. As palhetas geralmente são curvas e sua espessura diminui gradualmente,
sendo maior na base do que na extremidade: isto torna a palheta mais rígida e aumenta um
pouco a velocidade critica. Observação: não deve ser utilizado em vigas não uniformes.
5.18 - EIXOS ESCALONADOS
Quando o eixo tem os diâmetros escalonados como o do rotor de dois discos mostrados
na figura 22, a constante da mola torcional é variável. Pode-se determinar uma constante
equivalente kt em função das constantes individuais kl, k2, k3...Kn. Para molas em série, o
torque instantâneo T em cada seção do eixo é o mesmo. Entretanto, os ângulos de torção
diferentes. O ângulo total de torção Φt é a soma de todos os ângulos individuais de torção.
1 1 2 3
T T T T
... n
...
T
kt k1 k2 k3 kn
1 1 1 1
...
1
kt k1 k2 k3
1 1
kt k
kn
(50)
Para o rotor com dois discos e com eixos de diâmetro variável, pode-se substituir kt,
determinado pela equação (50).

37. 164
Figura 19 - Eixo e mancais
5.19 – EXERCÍCIOS PROPOSTOS - DIMENSIONAMENTO DE EIXOS
1. O eixo da figura suporta uma engrenagem cilíndrica de dentes retos para uma rotação de
315 rpm. O diâmetro primitivo da engrenagem é de 364 mm, t=310mm, t1=120 mm,
t2=190 mm. Dimensione este eixo, calculando o valor de d. A engrenagem é enchavetada
no eixo. A carga total atuando no eixo é de 15 KN.
Figura 21 - Exercício proposto 1.
2. Um eixo é fabricado com aço AISI 1137, laminado a frio, e é usado em um cortador de
grama. A potência é suprida ao eixo por uma correia plana à polia A. Em B, uma corrente
de rolos exerce uma força vertical e em C uma correia trapezoidal também exerce uma
força vertical. Nas condições de operação a correia transmite 35 HP a 425 rpm das quais
25 HP é transmitida ao cortador e 10 HP para o ventilador. As duas seções do eixo são

38. 165
unidas por um acoplamento flexível em D e as polias são todas enchavetadas no eixo.
Decida qual serão os diâmetros dos eixos, utilizando a teoria de falhas de Von Mises e o
critério de Goodman.
Figura 22 - Exercício proposto 2.

39. 166
3. Um eixo S de aço AISI 1137, laminado a frio, transmite potencia que recebe de um eixo
W, que gira a 2000 rpm através de uma engrenagem E de 125 mm de diâmetro à
engrenagem A de 375 mm de diâmetro. A potência é transmitida de uma engrenagem C
para a engrenagem G, que varia de 10 HP a 100 HP, retornando a 10 HP, durante uma
rotação de do eixo S. O projeto leva em conta as tensões variáveis e a teoria da máxima
tensão cisalhante TMT|C e o critério de Goodman. Para um fator de projeto n=1,8,
calcule o diâmetro do eixo, utilizando somente as cargas tangenciais motoras.
Figura 23 - Exercício proposto 3.

40. 167
4. Idêntico ao anterior, exceto que as componentes radiais das engrenagens devem também
ser consideradas, todas as engrenagens com ângulo de pressão 20o
.
5. Idêntico ao exercício 4, exceto que a engrenagem G se posiciona em cima da
engrenagem C.
6. Um pequeno eixo é fabricado com aço SAE1035, laminado a quente, recebe potência de
30 HP a 300 rpm, através de uma engrenagem de 300 mm de diâmetro, sendo esta
potência transmitida a outro eixo através de um acoplamento flexível. A engrenagem é
enchavetada no meio do eixo entre dois mancais, com ângulo de pressão 20o
, fator de
segurança n=1,5.
(a) Desprezando a componente radial R da carga total W, determine o diâmetro do eixo.
(b) Considerando ambas componentes radiais e tangencial, determine o diâmetro do
eixo.
Figura 24 - Exercício proposto 6.