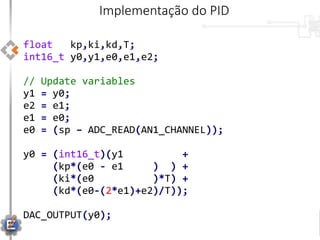
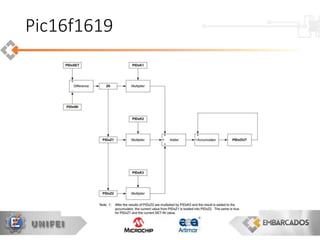
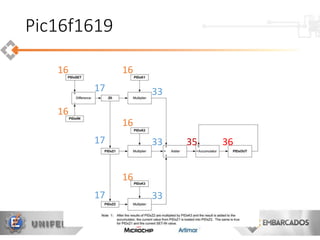
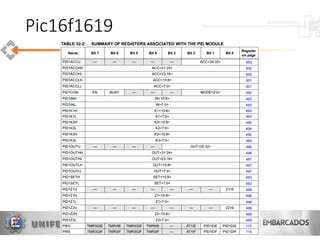
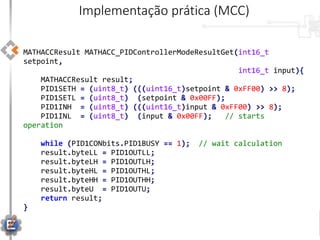
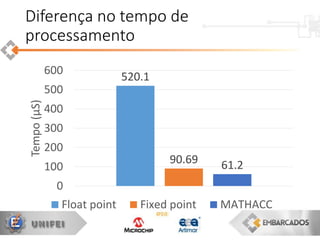
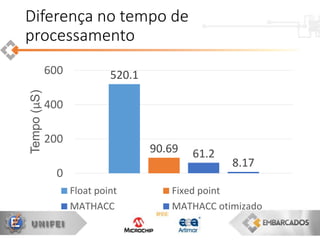
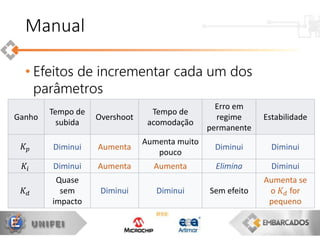
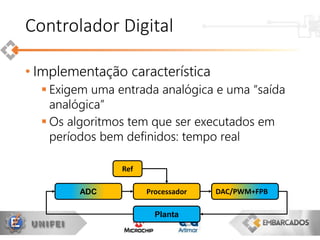
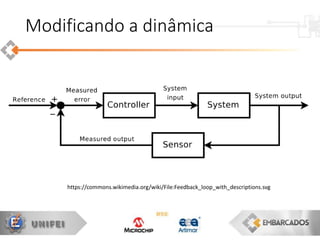
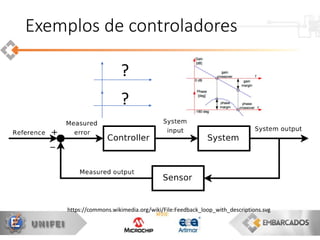
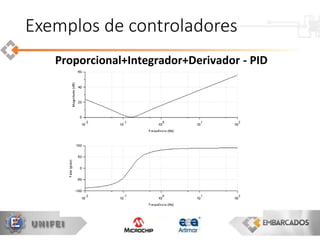
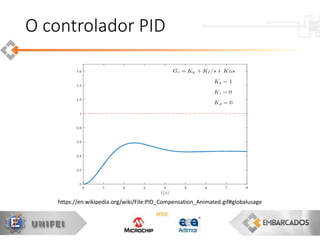
O documento apresenta uma visão geral sobre a implementação e teoria do controle PID, destacando as diferenças entre sistemas analógicos e digitais, além de discutir questões práticas e limitações do controlador PID. Ele aborda conceitos fundamentais como discretização, otimização de equações e processamento em tempo real, utilizando a plataforma PIC16F1619 para aplicação prática. Exemplos de implementações de código para PID em pontos flutuantes e fixos também são fornecidos.

2. Matemática e
Modelos dinâmicos
Mundo real
Computação e
Eletrônica
Visão geral
Implementação
prática
Teoria de
controle
Limitações e
requisitos
Controle

3. • O que é o PID?
• Como eu implemento o PID?
• Como eu implemento o PID para que ele
funcione na prática?
• Como eu implemento o PID para que ele
funcione na prática e a planta obedeça
meus requisitos?
Perguntas deste workshop

4. • Teoria de Controle
 PID
• Controle discreto
 Domínio contínuo x Domínio discreto
• Controle digital
 Implementações práticas
• Sintonizando o PID
 Identificação de sistemas
Índice

5. Introdução

6. • Problemas com controladores analógicos:
 Componentes eletrônicos tem suas
características modificadas com o tempo
• Principalmente capacitores
 É complicado modificar e ajustar os
parâmetros para uma determinada operação
Porquê Digital?

7. • Implementação característica
 Exigem uma entrada analógica e uma “saída
analógica”
 Os algoritmos tem que ser executados em
períodos bem definidos: tempo real
Controlador Digital
ProcessadorADC DAC/PWM+FPB
Planta
Ref

8. O que é
controle?

9. • Primeiras abordagens ao controle
 On/Off
 Histerese
 Proporcional
Introdução ao controle

10. • On/Off
sp = ADC_READ(AN1_CHANNEL);
ad = ADC_READ(AN2_CHANNEL);
if (ad >= sp ){
IO_RA5_SETLOW();
}else if (ad < sp ){
IO_RA5_SETHIGH();
}
Introdução ao controle
https://www.ibiblio.org/kuphaldt/socratic/doc/topical.html

11. • Histerese
hist = 100;
sp = ADC_READ(AN1_CHANNEL);
ad = ADC_READ(AN2_CHANNEL);
if (ad > (sp+hist)){
IO_RA5_SETLOW();
}else if (ad < (sp-hist)){
IO_RA5_SETHIGH();
}
Introdução ao controle
http://www.talkingelectronics.com/projects/50%20-
%20555%20Circuits/50%20-%20555%20Circuits.html

12. • Proporcional
sp = ADC_READ(AN1_CHANNEL);
ad = ADC_READ(AN2_CHANNEL);
err = sp-ad;
if (err > 255)
err = 255;
if (err < 0)
err = 0;
DAC1_SetOutput(err);
Introdução ao controle
http://www.spiraxsarco.com/Resources/Pages/Steam-
Engineering-Tutorials/basic-control-theory/basic-control-
theory.aspx

13. Teoria de
controle

14. • Mudança no objetivo
 Não importa mais apenas o valor da variável,
mas também como o sistema vai chegar no
valor desejado
 Controlar tanto o valor quanto o
comportamento de uma variável
Teoria de controle

15. • Comportamento de um sistema
 Como o estado atual é modificado quando as
entradas são alteradas;
 Como o sistema se altera com o passar do
tempo;
 Como o sistema se comporta na presença de
algum ruído ou distúrbio.
Dinâmica

16. • A saída depende das
entradas e do estado
atual do sistema
 Isto acontece pois a
maioria dos sistemas
possuem algum modo
de armazenar energia
Dinâmica
https://www.kitchensoap.com/2009/05/06/m
echanical-analogies-to-web-stuff-part-2/

17. • O mais comum é apresentar a dinâmica
do sistema através das funções de
transferência
Dinâmica
𝑉𝑅1 =
𝑉𝑓𝑜𝑛𝑡𝑒
𝑅1 + 𝑅2
∗ 𝑅2

18. • A maioria das dinâmicas possuem
comportamentos que só podem ser
expressados por equações diferenciais
(ED)
 A manipulação de ED’s é mais simples no
domínio da frequência;
 É comum o uso da transformada de Laplace.
Dinâmica
𝐹(𝑠) = 0
∞
𝑓 𝑡 𝑒−𝑠𝑡
𝑑𝑡

19. Dinâmica
http://www.cbcity.de/this-animation-will-tell-you-everything-about-the-connection-between-
time-and-frequency-domain-of-a-signal

20. • Funções de transferência:
 As raízes da equação do
numerador são
denominadas zeros;
 As raízes da equação do
denominador são
denominadas polos;
 A estabilidade do sistema
está inerentemente
relacionada à quantidade e
tipos de polos e zeros.
Dinâmica

21. Dinâmica
𝐹 𝑠 =
1
(𝑠 + 𝑎)(𝑠 + 𝑏)
𝑎, 𝑏 > 0
𝑎, 𝑏 = 0
𝑎, 𝑏 < 0
𝑎, 𝑏 reais
𝑓 𝑡 = 𝑐1 𝑒−𝑎𝑡
+ 𝑐2 𝑒−𝑏𝑡

22. Dinâmica
𝐹 𝑠 =
1
(𝑠 + 𝑎)(𝑠 + 𝑏)
𝑓 𝑡 = 𝐶1 𝑒−𝑝 𝑟 𝑡
∗ cos 𝑝𝑖 ∗ 𝑡 + 𝐶2 𝑒−𝑝 𝑟 𝑡
∗ sin 𝑝𝑖 ∗ 𝑡
𝑎, 𝑏 ⇒ 𝑝 𝑟 ± 𝑝𝑖 𝑖𝑎, 𝑏 imaginários

23. Dinâmica
http://www.peterstone.name/Maplepgs/ord2DEs.html

24. Modificando a
dinâmica

25. Modificando a dinâmica
https://commons.wikimedia.org/wiki/File:Feedback_loop_with_descriptions.svg

26. • Modifica-se o comportamento alterando
os ganhos dos sinais em diferentes
frequências
 Altas frequências -> mudanças rápidas
 Baixas frequências -> mudanças lentas
Modificando a dinâmica

27. Exemplos de controladores
https://commons.wikimedia.org/wiki/File:Feedback_loop_with_descriptions.svg
?
?

28. Os efeitos do PID

29. • Diagrama de bode
 Composto de 2 gráficos
• Superior: Apresenta o ganho a ser aplicado em
cada faixa de frequência
• Inferior: Apresenta a variação no ângulo do sinal
para aquela frequência.
Exemplos de controladores

30. Exemplos de controladores
Proporcional+Integrador+Derivador - PID

31. O controlador PID
https://en.wikipedia.org/wiki/File:PID_Compensation_Animated.gif#globalusage

32. • Problemas do PID
 Em geral não conseguem implementar “controle
ótimo”
 Problemas para operar com não linearidades
 Ruídos na parte derivativa
• Geralmente implementa-se um passa baixa para
corrigir
 Integral windup
• A parte integral acumula muito “erro” e demora a
retornar a valores aceitáveis
 Mudanças bruscas no Set-Point
Controlador PID

33. Discretização

34. • Sistema amostrado
Discretização
https://www.kullabs.com/classes/subjects/unit
s/lessons/notes/note-detail/7424

35. • Amostragem
 Nyquist: dobro da maior frequência
Discretização
https://www.adinstruments.com/tips/data-quality

36. • Problema:
 O mundo funciona em s (contínuo)
 O micro funciona em z (discreto)
• Relação entre z e s
 𝑋∗(𝑠) = 𝑋(𝑧)| 𝑧=𝑒 𝑠𝑇
Discretização

37. • Aproximações de 𝑧 = 𝑒 𝑠𝑇
 Forward
 Backward
 Bilinear
Discretização

38. • Aproximações de s para z
 Forward
• 𝑠 =
𝑧−1
𝑇
 Backward
• 𝑠 =
𝑧−1
𝑧𝑇
 Bilinear
• 𝑠 =
2
𝑇
𝑧−1
𝑧+1
Discretização

39. O PID discreto

40. • Equação do PID
 𝐾𝑝 +
𝐾 𝑖
𝑠
+ 𝐾 𝑑 ∗ 𝑠
PID em S

41. • Backward
 𝐾 𝑝 +
𝐾 𝑖
𝑠
+ 𝐾 𝑑 ∗ 𝑠

𝑦 𝑧
𝑒 𝑧
= 𝐾𝑝 + 𝐾𝑖
𝑧𝑇
𝑧−1
+ 𝐾 𝑑 ∗
𝑧−1
𝑧𝑇

𝑦 𝑧
𝑒 𝑧
=
𝐾 𝑝 𝑧2−𝑧 +𝑇𝐾𝑖 𝑧2 +
𝐾 𝑑
𝑇
(𝑧2−2𝑧+1)
𝑧2−𝑧
 𝑦 𝑧 𝑧2 − 𝑧 = 𝑒 𝑧
𝐾 𝑝 𝑧2
− 𝑧 + 𝑇𝐾𝑖 𝑧2
+
𝐾 𝑑
𝑇
(𝑧2
− 2𝑧 + 1)
Discretização

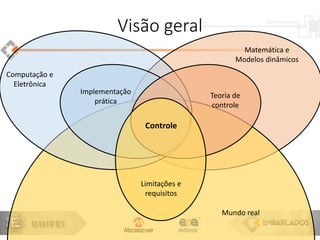
42. • Transformada Z inversa
 𝑥[𝑛] = 𝒵−1{𝑋(𝑧)} =
1
2𝜋𝑗 𝐶
𝑋(𝑧)𝑧 𝑛−1 𝑑𝑧
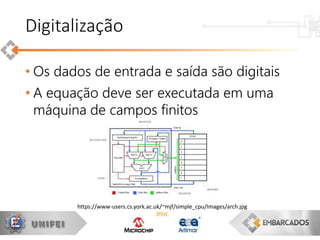
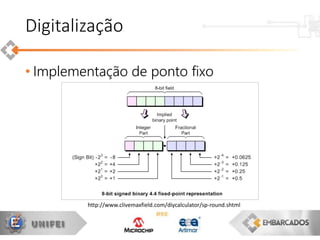
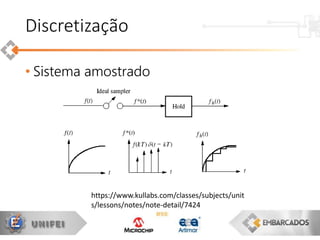
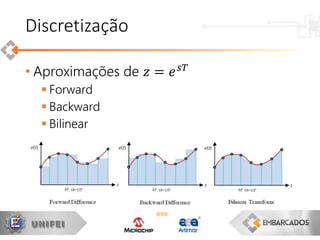
Discretização
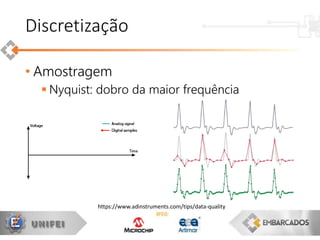
•Frequência
discreta
•Tempo
discreto
•Frequência
contínua
•Tempo
contínuo
T S
ZN

43. • PID no domínio N
 Permite a implementação do PID utilizando
uma equação à diferenças
 O valor atual da saída é baseado no valor
atual do erro e nos valores anteriores
 Possui o tempo de amostragem como
coeficiente da equação
Discretização

44. • Backward
 𝑦 𝑧 𝑧2
− 𝑧 = 𝑒 𝑧
𝐾 𝑝 𝑧2 − 𝑧 + 𝑇𝐾𝑖 𝑧2 +
𝐾 𝑑
𝑇
(𝑧2
− 2𝑧 + 1)
 Multiplicando por 𝑧−2
:
 𝑦 𝑧 1 − 𝑧−1 = 𝑒 𝑧
𝐾 𝑝 1 − 𝑧−1
+ 𝑇𝐾𝑖
+
𝐾 𝑑
𝑇
1 − 2𝑧−1 + 𝑧−2
 𝑦 𝑛 = 𝑦 𝑛 − 1 + 𝐾 𝑝 𝑒 𝑛 − 𝑒 𝑛 − 1 +
𝑇𝐾𝑖 𝑒 𝑛 +
𝐾 𝑑
𝑇
(𝑒 𝑛 − 2𝑒 𝑛 − 1 + 𝑒 𝑛 − 2 )
Discretização

45. • Backward
 𝑦 𝑧 1 − 𝑧−1
= 𝑒 𝑧
𝐾𝑝 1 − 𝑧−1 + 𝑇𝐾𝑖
+
𝐾 𝑑
𝑇
1 − 2𝑧−1 + 𝑧−2
 𝑦 𝑛 = 𝑦 𝑛 − 1 +
𝐾𝑝 𝑒 𝑛 − 𝑒 𝑛 − 1 +
𝑇𝐾𝑖 𝑒 𝑛 +
𝐾 𝑑
𝑇
(𝑒 𝑛 − 2𝑒 𝑛 − 1 + 𝑒 𝑛 − 2 )
Discretização

46. float kp,ki,kd,T;
int16_t y0,y1,e0,e1,e2;
// Update variables
y1 = y0;
e2 = e1;
e1 = e0;
e0 = (sp – ADC_READ(AN1_CHANNEL));
y0 = (int16_t)(y1 +
(kp*(e0 - e1 ) ) +
(ki*(e0 )*T) +
(kd*(e0-(2*e1)+e2)/T));
DAC_OUTPUT(y0);
Implementação do PID

47. • Problemas com as equações
 Integral windup (saída fica com valor muito
grande por causa do somatório)
• Solução
 Saturar a saída
Discretização

48. Digitalização
Quantização

49. • Os dados de entrada e saída são digitais
• A equação deve ser executada em uma
máquina de campos finitos
Digitalização
https://www-users.cs.york.ac.uk/~mjf/simple_cpu/Images/arch.jpg

50. • Tipo de dados:
 Números inteiros
 Ponto flutuante
 Ponto fixo
Digitalização
https://commons.wikimedia.org/wiki/File:IEEE_754_Single_Floating_Point_Format.svg

51. 520.1
90.69
0
100
200
300
400
500
600
Tempo(μS)
Float point Fixed point
Diferença no tempo de
processamento

52. • Implementação de ponto fixo
Digitalização
http://www.clivemaxfield.com/diycalculator/sp-round.shtml

53. • Todos os números estão multiplicados por
um valor base
 O valor escolhido é geralmente da base 2
• Isto permite usar bit shift para multiplicar/dividir
• Algumas operações devem ser corrigidas
Digitalização

54. • Exemplo:
 Soma e subtração permanecem iguais
• Ex: R$4,00+R$1,23 = 400+123
= 523 (R$5,23)
 Multiplicação tem que ser corrigida
• Ex: R$4,00 * 1,23kg = 400*123 = 49.200/100
= 492 (R$4,92)
• Dividi-se o resultado pelo valor base
 Divisão também tem que ser corrigida
• Ex: 4,00km / 1,23l = 400 / 123 = 3*100
= 300 (3,00km/l)
• Multiplica-se o resultado pelo valor base
Digitalização

55. Otimização da
equação
Reduzindo a quantidade de cálculos

56. • Uma otimização interessante é reescrever
as equações colocando em evidência os
erros anteriores.
 Isto reduz o cálculo para apenas 3
multiplicações
Otimização da equação

57. • Equação do PID:
 Ponto fixo
 Em função dos erros
 Coeficientes redefinidos
• k1 = (kp + ki*T + kd/T) *
SHIFT;
• k2 = -((kp + 2*kd/T) *
SHIFT);
• k3 = (kd/T) * SHIFT;
 kp, ki, kd e T definidos
como float.
int16_t k1,k2,k3;
int16_t y0,y1, e0,e1,e2;
// Update variables
y1 = y0;
e2 = e1;
e1 = e0;
e0 = (sp - READ_AD());
y0 = (((int32_t) k1 * e0) +
((int32_t) k2 * e1) +
((int32_t) k3 * e2));
y0 = y0>>8 + y1;
Otimização da equação

58. Tempo real
Porque o T de 𝑧 = 𝑒 𝑠𝑇 é constante.

59. • Necessidade de manter tempo real
 Toda teoria de controle digital baseada na
transformada Z exige T fixo
• de 𝑧 = 𝑒 𝑠𝑇
 T é um ciclo de processamento completo
• Amostragem do sinal, processamento e
atualização da saída
Tempo Real

60. • Como implementar?
 Timer start/wait
 Interrupção do timer
 RTOS
Tempo Real

61. PIC16f1619
Pois as vezes nem fixed point é suficiente.

62. • Características importantes:
 ADC 10 bits
 2 PWM 10 bits
 DAC 8 bits
 5 timers (Real time)
 MATH ACC PID
Pic16f1619

63. Pic16f1619

64. Pic16f1619

65. • Equação do PID:
 Backward/ponto fixo/função do erro
 k1 = (kp + ki*T + kd/T) * SHIFT;
 k2 = -((kp + 2*kd/T) * SHIFT);
 k3 = (kd/T) * SHIFT;
Otimização da equação

66. Pic16f1619
16
16
16
16
16
17
17
17
35
33
33
33
36

67. Pic16f1619

68. Implementação
prática

69. • Microchip Code Configurator®
 Utilizado para gerar os drivers dos periféricos
• Timer 0 e 2
• ADC
• PWM
• GPIO’s
MCC

70. • Projeto exemplo:
https://github.com/rmaalmeida/PID_pic16f1619.X
 Alterações nas libs geradas
• TMR0_Reload() não reseta a flag do timer
• Mathacc.c não possui funções para carregar K1,
K2 e K3
 Realtime garantido por timer overflow
• Tciclo > Tprocessamento
PID_pic16f1619

71. int16_t pid_sw_float(int16_t ad) {
f_y1 = f_y0; f_e2 = f_e1;
f_e1 = f_e0; f_e0 = ((float) sp) - ad;
f_y0 = (f_k1 * f_e0) +
(f_k2 * f_e1) +
(f_k3 * f_e2);
f_y0 += f_y1;
if (f_y0 > MAX_SAT) {
f_y0 = MAX_SAT;
} else if (f_y0 < MIN_SAT) {
f_y0 = MIN_SAT;
}
return (int16_t) f_y0;
}
Implementação prática (float)

72. int16_t pid_sw_fixed(int ad) {
i_y1 = i_y0; i_e2 = i_e1;
i_e1 = i_e0; i_e0 = (sp - ad);
i_y0 = (((int32_t) i_k1 * i_e0) +
((int32_t) i_k2 * i_e1) +
((int32_t) i_k3 * i_e2));
i_y0 = i_y0 >> 8;
i_y0 += i_y1;
if (i_y0 > MAX_SAT) {
i_y0 = MAX_SAT;
} else if (i_y0 < MIN_SAT) {
i_y0 = MIN_SAT;
}
return i_y0;
}
Implementação prática (fixo)

73. MATHACCResult MATHACC_PIDControllerModeResultGet(int16_t
setpoint,
int16_t input){
MATHACCResult result;
PID1SETH = (uint8_t) (((uint16_t)setpoint & 0xFF00) >> 8);
PID1SETL = (uint8_t) (setpoint & 0x00FF);
PID1INH = (uint8_t) (((uint16_t)input & 0xFF00) >> 8);
PID1INL = (uint8_t) (input & 0x00FF); // starts
operation
while (PID1CONbits.PID1BUSY == 1); // wait calculation
result.byteLL = PID1OUTLL;
result.byteLH = PID1OUTLH;
result.byteHL = PID1OUTHL;
result.byteHH = PID1OUTHH;
result.byteU = PID1OUTU;
return result;
}
Implementação prática (MCC)

74. temp = MATHACC_PIDControllerModeResultGet(sp, ad);
res = (((int32_t) (temp.byteU&0x7)) << 24)+
(((int32_t) temp.byteHH) << 16) +
(((int16_t) temp.byteHL) << 8) +
temp.byteLH;
if (temp.byteU & 0x04) { res |= 0xf8000000; }
if (res > 1023) {
res = 1023;
PID1OUTLL = 0; PID1OUTLH = 0xff;
PID1OUTHL = 0x3; PID1OUTHH = 0;
PID1OUTU = 0;
} else if (res < 0) {
res = 0;
MATHACC_ClearResult();
}
Usando o MATHACC

75. 520.1
90.69 61.2
0
100
200
300
400
500
600
Tempo(μS)
Float point Fixed point MATHACC
Diferença no tempo de
processamento

76. • Código gerado pelo MCC
 Não possui saturação
 Retorna todas as variáveis (5bytes)
 Sempre reescreve o setpoint
 Não corrige o offset do ponto fixo
 Não verifica overflow
Pic16f1619

77. Otimizando o
MATHACC
Entrada e saída com 10 bits
Coeficientes em formato Q7.8
Saturando em 0 e 1023 (10bits)

78. int16_t MATHACC_PIDResult(int16_t input) {
int16_t temp;
PID1INH = (uint8_t) (((uint16_t) input & 0xFF00) >> 8);
PID1INL = (uint8_t) (input & 0x00FF); // starts module
operation
while (PID1CONbits.PID1BUSY == 1); // wait for complete
temp = (((int16_t) PID1OUTHL) << 8) + PID1OUTLH;
if (PID1OUTU & 0x04) { //verifica se negativo
temp = 0;
MATHACC_ClearResult();
//verifica overflow
}else
if(((PID1OUTU&0x07)!=0)||(PID1OUTHH!=0)||(PID1OUTHL&0xFC)){
temp = 1023;
PID1OUTLL = 0;
PID1OUTLH = 0xff;
PID1OUTHL = 0x3;
PID1OUTHH = 0;
PID1OUTU = 0;
}
return temp;
}
Otimizando o MATHACC

79. 520.1
90.69 61.2
8.17
0
200
400
600
Tempo(μS)
Float point Fixed point
MATHACC MATHACC otimizado
Diferença no tempo de
processamento

80. Comportamento
dinâmico

81. Kp=1, Ki=0, Kd=0, Ta = 1ms

82. Kp=1, Ki=10, Kd=0, Ta = 1ms

83. Kp=1, Ki=100, Kd=0, Ta = 1ms

84. Kp=1, Ki=100, Kd=0.01, Ta = 1ms

85. Kp=1, Ki=100, Kd=0, Ta = 10ms

86. Kp=5, Ki=100, Kd=0,01, Ta = 10ms

87. Sintonia do PID

88. Sintonia do PID
• Objetivos
 Controlar uma grandeza
 Modificar o comportamento do sistema
• Métodos
 Empíricos
 Compensação

89. Sintonia do PID
• Empíricos
 Manual
 Sensibilidade limite
 Curva de reação

90. • Efeitos de incrementar cada um dos
parâmetros
Manual
Ganho
Tempo de
subida
Overshoot
Tempo de
acomodação
Erro em
regime
permanente
Estabilidade
𝐾 𝑝 Diminui Aumenta
Aumenta muito
pouco
Diminui Diminui
𝐾𝑖 Diminui Aumenta Aumenta Elimina Diminui
𝐾 𝑑
Quase
sem
impacto
Diminui Diminui Sem efeito
Aumenta se
o 𝐾 𝑑 for
pequeno

91. • Baseado na resposta em malha fechada
• O sistema é levado a oscilação apenas
com ganho proporcional
 O sistema deve ser capaz de oscilar
Sensibilidade limite

92. • Aumenta-se o ganho proporcional até o
sistema começar a oscilar.
 Este será o valor de Kc (ganho crítico)
• Mede-se o Tc (período da oscilação)
Ziegler-Nichols MF
Tipo 𝐾 𝑝 𝑇𝑖 𝑇𝑑
P 0,5𝐾𝑐 ∞ 0
PI 0,4𝐾𝑐 0,8𝑇𝑐 0
PID 0,6𝐾𝑐 0,5𝑇𝑐 0,125𝑇𝑐

93. Ziegler-Nichols MF
https://electronics.stackexchange.com/questions/118174/pid-controller-and-ziegler-nichols-method-how-to-get-oscillation-period

94. • É baseado na resposta em malha aberta
do sistema
 Utiliza-se um degrau para análise do sistema
• A resposta deve possuir o formato de uma
curva em S
Curva de reação

95. Ziegler-Nichols MA
• Sintonia do PID
Tipo 𝐾 𝑝 𝑇𝑖 𝑇𝑑
P
𝑇
𝐿
∞ 0
PI 0,9
𝑇
𝐿
𝐿
0,3
0
PID 1,2
𝑇
𝐿
2𝐿 0,5𝐿
Ref
L T

96. • Sintonia manual
• Métodos empíricos
• Alocação de polos
 Necessita de conhecimento da equação da
planta
 Através de definições de tempo de
acomodação e máximo overshoot permite
encontrar Kp, Ki, Kd.
Sintonia de PID

97. Obrigado
Rodrigo M A Almeida
rodrigomax@unifei.edu.br
@rmaalmeida