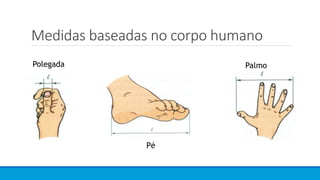
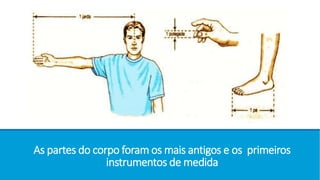
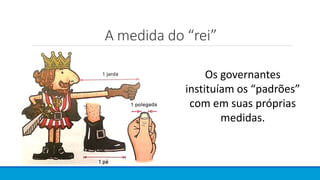
O documento descreve a evolução histórica das grandezas e medidas, desde as primeiras referências ao corpo humano até a padronização do Sistema Internacional de Unidades. Inicialmente, medidas variavam entre culturas e locais, mas houve um esforço para estabelecer padrões universais, culminando na definição do metro e do quilograma em termos invariables da natureza.

1. Preparo Material e orientação técnica – SME
2º Encontro Matemática –Abril/2015
15 – 22 - 23
Grandezas e Medidas

2. Epígrafe:
"O homem é a medida de todas
as coisas..."
Protágoras de Abdera

3. Leitura: Uma menina do seu
tamanho, cap I do livro de
Ana Maria Machado
Considerada pela crítica como uma das mais
versáteis e completas das escritoras brasileiras
contemporâneas, a carioca Ana Maria Machado
ocupa a cadeira numero 1 da Academia Brasileira de
Letras, que presidiu de 2011 a 2013.
Jornalista
Ana Maria Machado é uma jornalista, professora,
pintora e escritora brasileira.
Nascimento: 24 de dezembro de 1941 (73 anos), Rio
de Janeiro, Rio de Janeiro
Nacionalidade: Brasileira
Educação: Universidade Federal do Rio de Janeiro
Filme: Noites Cariocas
Prêmio: Prêmio Hans Christian Andersen: Escritor

4. Objetivos deste encontro
Refletir sobre a importância do ensino de Grandezas e Medidas.
Construir a ideia de grandeza e de medida.
Reconstruir o conhecimento de grandezas e medidas ao longo da história.
Contextualizar o uso social de unidades padronizadas e não padronizadas.
Refletir sobre os princípios que devem permear todo o estudo de medidas.
Analisar situações didáticas com foco nas expectativas de aprendizagem referentes ao
bloco de conteúdos Grandezas e Medidas.

5. Organizando nosso conhecimento.
Vídeo: Debate Grandezas e Medidas – Salto para o futuro – 15min
https://www.fnde.gov.br/sigefweb/index.php/declaracao-rendimento

6. Qual a importância de se trabalhar “Grandezas e Medidas” como um dos
blocos de conteúdo na área de matemática no Ensino Fundamental?

7. São essenciais para o desenvolvimento do raciocínio matemático e do
desenvolvimento científico, posterior ao ciclo de alfabetização
Na vida em sociedade as grandezas e medidas estão presentes em quase
todas as atividades realizadas
O tema proporciona situações muito interessantes para articulação entre
outros blocos como números ,operações . geometria e com outras áreas do
conhecimento
O trabalho com este bloco oferece oportunidades nas quais as crianças
possam identificar propriedades dos objetos e estabeleçam comparações

8. Como você aprendeu sobre este bloco de conteúdos?
Havia relação com a sua vida, eram significativas?

9. Onde era colocado ênfase neste conteúdo?
Em trabalhar mecanicamente transformações de múltiplos submúltiplos sem
nenhuma contextualização (influência Matemática moderna)

10. Aplicação de fórmulas “incompreensíveis” para cálculo de área e perímetro

11. Era um conteúdo muitas vezes delegado a segundo plano e final do livro
didático.

12. O que você entende sobre
grandezas?
Vamos olhar para as expectativas do Bloco Grandezas e
Medidas e observar quais as grandezas então presentes?
massa comprimento
área capacidade
tempo
perímetro
Valor
monetário
temperatura

13. Expectativa de aprendizagem (grandezas e medidas)-1ºano
- Identificar dias da semana e do mês, explorando o calendário. (Unid 1,3,4- Vol.1) ( Unid 5 Vol. 2)
- Relacionar dia, mês e ano presentes na escrita de uma data. (Unid 3 – Vol. 1) ( Unid 5 – Vol. 2)
- Identificar comprimentos, utilizando passos, palmos e também a fita métrica e a régua.(Unid 4- Vol. 1) (Unid 5-8 vol. 2)
- Identificar capacidades, utilizando recipientes diversos e também o litro. (Unid 6 – Vol. 2)
- Identificar massas, utilizando balanças e conhecendo o quilograma. (Unid.7 Vol. 2)
- Identificar objetos que podem ser comprados por unidades de massa ou capacidade. (Unid.7 Volume 2)
- Realizar estimativas relativas a medições. (Unid 5,7,8 – vol. 2)
- Reconhecer algumas cédulas e moedas do sistema monetário brasileiro usadas no dia a dia. (Unid 3 – vol 1)
- Identificar que um dia tem 24 horas. (Unid 4 – vol. 1)

14. Por exemplo: quais atributo usaríamos para comparar duas varetas?

15. Entendendo Grandezas:
Grandezas são consideradas e percebidas
como atributos ou propriedades de objetos.
Escolhido um atributo, podemos comparar
objetos segundo esse atributo
É tudo aquilo que pode ser medido, ou seja
quantificado

16. O que é medir?
De modo simples medir significa comparar grandezas de
mesma natureza, sendo o resultado de cada medição
expresso por um número e por uma unidade de medida.

17. O que são medidas de mesma natureza?
Para medir o tempo usamos intervalos de tempo ( dias, horas, minutos etc)
Para medir comprimento usamos unidade de comprimento ( metro, centímetro, etc)
Nesse sentido, a unidade escolhida é sempre de mesma natureza do elemento a ser
medido.

18. Então, o que significa medir?
Na prática escolhemos uma unidade e contamos quantas vezes a menor cabe na
medida maior.
Medir também é contagem mediada por uma unidade arbitrária ou padrão

19. Quando é que a criança começa a medir?
Antes mesmo de a criança ir para a escola, ela
passa por experiências diversas, as quais, na
maioria das vezes, relacionam-se com as
medidas. São eventos culturais como idas ao
mercado, trajetos percorridos, tempo para
tomar banho, escovar os dentes, comer,
brincar, usar o computador, ver TV, servir
refeição, fazer bolos, doces, encher vasilha,
crescer etc. Eventos “corriqueiros”, que desde
muito cedo desenvolvem na criança sua
percepção de espaço, tempo, massa,
capacidade, velocidade etc. Isto nos aponta a
necessidade de o professor conhecer cada vez
mais e melhor o contexto sociocultural do
público com o qual trabalha.

20. Como trabalhar em
sala de aula com
nossos alunos de 1º
ano atividades que
os levem a construir
conceitos de
medidas de tempo,
comprimento, massa
e capacidade de
forma significativa?
Segundo estudos relativos a aprendizagem do
conceito de grandeza, é importante não associar
a medida da grandeza diretamente à grandeza,
como tradicionalmente era realizado. Antes,
deve-se construir a noção de grandeza partindo
das experiências e vivências dos alunos,
considerando capacidades, como a observação,
a manipulação, a estimativa, a percepção para
então se estabelecerem as relações, durante
todo ano letivo.

21. “Com frequência, as primeiras aproximações
dos meninos e das meninas a estes temas
envolvem experiências as quais aparecem
balanças, réguas e jarras graduadas. No
entanto, temos que advertir que o uso de
instrumentos de medição, anterior a realização
de medições com unidades não
convencionais, pode impedir que a infância
percorra um caminho parecido ao que
percorreu a humanidade até chegar a medir.
Em realidade somente assim se chega ao
conceito de medida. A mera aplicação de um
instrumento de medida somente expressa um
resultado numérico e isto não é medir, é ler
uma medição”
Duwalde Cuberes – 2007 – Encuentros Cercanos com la matematica

22. As crianças são curiosas e observadoras e já
fazem comparações de acordo com suas
necessidade percorrendo caminho que a
humanidade fez para construir este
conhecimento, mas este caminho deve ser
mediado pela escola proporcionando
experiências concretas para que o aluno
construa o conhecimento das grandezas e
medidas e este adquira significado para elas.

23. O homem como medida
Os povos antigos
elaboraram sistemas de
medidas que faziam
referência às medidas do
corpo humano.
Homem Vitruviano de Leonardo da Vinci

24. Medidas baseadas no corpo humano
Polegada Palmo
Pé

25. As partes do corpo foram os mais antigos e os primeiros
instrumentos de medida

26. Cúbito ou côvado
O côvado foi uma unidade de
medida usada por vários povos
antigos, entre eles os babilônios,
egípcios e hebreus.
Considerada como a medida da
distância entre o dedo médio e o
cotovelo.

27. As medidas variam de
pessoa para pessoa
Confusão na medição
Necessidade de estabelecer
padrões para as medidas

28. A medida do “rei”
Os governantes
instituíam os “padrões”
com em suas próprias
medidas.

29. Medidas da Arca de Noé - Bíblia
“De trezentos côvados o
comprimento da arca, e
de cinquenta côvados a
sua largura, e de trinta
côvados a sua altura.”
Gênesis 6:15
https://www.bibliaonline.com.br/acf/gn/
6
"Tissot Building the Ark" por James Tissot -

30. Cúbito Padrão - Egito
Os egípcios criaram um cúbito padrão.

31. Muitos padrões diferentes...
CADA POVO TINHA SEUS
PRÓPRIOS PADRÕES
Cúbito sumério = 49,5 cm
Cúbito egípcio = 52,4 cm
Cúbito assírio = 54,9 cm
PADRÕES DIFERENTES ERAM
UTILIZADOS NUMA MESMA NAÇÃO.
EXE: INGLATERRA
Pé romano = 29,6 cm
Pé comum = 31,7 cm
Pé do Norte = 33,6 cm.

32. Tempo
Registravam as repetições dos fenômenos
periódicos.
Qualquer evento familiar servia para
marcar o tempo: o período entre um e
outro nascer do Sol, a sucessão das luas
cheias, ou a das primaveras, a posição das
estrelas no céu noturno.

33. Instrumentos para medir o tempo
Relógio de sol
Relógio de areia
Relógio d'agua
Relógio de pêndulo
http://efisica.if.usp.br/mecanica/ensinomedio/tempo/evolucao_relogios/

34. Conferindo a
medida padrão
Placas com os padrões
foram colocadas em locais
públicos para que a
população pudesse
conferir as medidas de
comprimento e de tempo.

35. Massa
O grão de trigo tirado
do meio da espiga,
provavelmente um dos
primeiros elementos
padronizados de peso.
Os egípcios inventaram a
balança para padronizar a
cobrança de impostos e a
quantidade de produção
agrícola.

36. Escambo
“A moeda, como hoje a conhecemos, é o resultado de
uma longa evolução. No início não havia moeda,
praticava-se o escambo, simples troca de mercadoria
por mercadoria, sem equivalência de valor.
Assim, quem pescasse mais peixe do que o necessário
para si e seu grupo trocava este excesso com o de
outra pessoa que, por exemplo, tivesse plantado e
colhido mais milho do que fosse precisar. “
http://www.bcb.gov.br/htms/origevol.asp?idpai=HISTDIN

37. Moeda mercadoria
“Algumas mercadorias, pela sua utilidade, passaram a ser mais procuradas do que outras.
Aceitas por todos, assumiram a função de moeda, circulando como elemento trocado por outros
produtos e servindo para avaliar-lhes o valor.”
http://www.bcb.gov.br/htms/origevol.asp?idpai=HISTDIN
Gado
Sal
Metal

38. Moedas
“Os utensílios de metal passaram a ser mercadorias muito
apreciadas.
A valorização, cada vez maior, desses instrumentos levou à
sua utilização como moeda e ao aparecimento de réplicas
de objetos metálicos, em pequenas dimensões, que
circulavam como dinheiro.
Surgem, então, no século VII a.C., as primeiras moedas
com características das atuais: são pequenas peças de
metal com peso e valor definidos e com a impressão do
cunho oficial, isto é, a marca de quem as emitiu e garante
o seu valor.”
http://www.bcb.gov.br/htms/origevol.asp?idpai=HISTDIN

39. A busca por um padrão universal
O uso de diferentes padrões de medidas entre as
nações e mesmo dentro de um único país
vigorou durante toda a Idade Moderna.
A decisão de criar um modelo de unidades que
fosse universal ganhou força com a Revolução
Francesa, em 1789. O rompimento com as
tradições feudais e absolutistas abriu caminho
para novas ideias.

40. Como seria essa “medida”?
“O plano era elaborar um sistema de unidades baseado num padrão
da natureza, imutável e indiscutível. Como a natureza não pertence a
ninguém, tal padrão poderia ser aceito por todas as nações, inclusive
a rival Inglaterra, “e se tornaria um sistema universal.”
(Superinteressante, ed. 186, mar. de 2003)

41. Metro (grego métron e significa “o que mede”
O metro “nasceu” sendo a décima
milionésima parte de um quarto do
meridiano terrestre (distância entre o
polo norte e o Equador).

42. Conferência Geral de Pesos e Medidas (1983)
Metro
• equivale a 299 792 458 avos da distância percorrida pela luz no vácuo durante um
segundo
Quilograma
• construído a partir de platina iridiada, com massa de 1 litro de água destilada a 4o
C.
Segundo
• 86400 avos do dia solar médio.
24 x 60 x 60 = 86400
• Hoje o segundo é definido tecnicamente como a duração de 9'192'631'770
períodos da radiação correspondente à transição entre dois níveis hiperfinos do
estado fundamental do átomo de césio 133

43. Paradoxo: Indicadores das avaliações externas nos chamam a atenção para o fato de embora
considerarmos fácil o bloco de conteúdo “Grandezas e Medidas” e tão presente em nosso cotidiano,
os alunos não tem demonstrado que desenvolveram habilidades para estimar a medida de
grandezas utilizando unidades de medidas convencionais ou não, no Brasil como em outros países,
como a França por exemplo.
Quem está segurando um objeto que mede, aproximadamente, 1 metro de comprimento?
(A)Luís
(B) Mauro
(C)Paulo
(D)Renato
Percentual de respostas às alternativas
A B C D
34% 8% 1% 55%

44. Em duplas analisem as situações problemas considerando as expectativas de
aprendizagens ;
1- Quais expectativas e grandezas estão contempladas em cada situação problema?
2- Quais habilidades os alunos precisam desenvolver para realizarem estas situações
problemas?
Análise de situações-problemas envolvendo Grandezas e Medidas.

45. OBSERVE O CALENDÁRIO DO MÊS DE MAIO DE 2015.A
FAMÍLIA DE LUCAS VAI AO BOSQUE NO DIA 3 DE MAIO. MARQUE
NO CALENDÁRIO O DIA DO MÊS DE LUCAS IRÁ AO BOSQUE
.
Questão 1:

46. QUESTÃO 2
CIRCULE O PRODUTO QUE NÃO PODE SER COMPRADO POR QUILO:

47. QUESTÃO 3
A PROFESSORA PEDIU PARA SEUS ALUNOS MEDIREM A TAMPA DE SUAS CARTEIRAS
COM AS MÃOS. O QUE SERÁ QUE VAI ACONTECER?
(OBS.: o registro das medidas será feitos pela professora em local visível aos alunos para
discussão).

48. Em duplas ou trios, discutam os princípios indicados por
seu formador e organize uma breve apresentação para a
turma relacionando com tudo que discutimos até o
momento.
Momento de Estudo:
Texto: “Doze princípios para o processo de aprendizagem e ensino
de grandezas e medidas” Muniz, Cristiano Alberto, Batista,
Carmyra Oliveira, Silva, Erondina Barbosa da.
Módulo III (Decimais, Medidas e Sistema Monetário Brasileiro) de educação e Linguagem Matemática. Brasília:
Universidade de Brasília, 2008

49. 1º Princípio — O ponto de partida do estudo de medidas é a percepção.
2º Princípio — O estudo das medidas deve perpassar todo o espaço curricular, deve estar
presente do primeiro ao último dia de aula.
3º Princípio — Todas as medidas devem iniciar com as unidades arbitrárias.
4º Princípio — A transferência da unidade arbitrária para a unidade padrão deve ser uma
decorrência de uma relação social do grupo em questão.
5º Princípio — A transferência da unidade padrão para a unidade legal deve estar
vinculada à história da civilização (de acordo com o nível de ensino).
6º Princípio — É de fundamental importância que a escola estabeleça a relação entre as
unidades legais com as unidades culturais, caso não queira alijar sua função social.
7º Princípio — No estudo de medidas é importante que conheçamos a real função da
manipulação de material concreto.
DOZE PRINCÍPIOS PARA O PROCESSO DE APRENDIZAGEM E ENSINO DE GRANDEZAS E MEDIDAS

50. 8º Princípio — É preciso trabalhar a real dimensão do sistema de medidas adotado pela nossa
cultura.
9º Princípio - Ao trabalhar com medidas, o professor deve ficar especialmente atento a esta
fragmentação curricular. Sua atitude deve ser no sentido de tentar vincular as medidas,
especialmente quando se trata de medidas de capacidade, de volume, de comprimento, de
superfície e de massa.
10º Princípio — Nós temos que aceitar e explorar a inter-relação entre medidas e geometria.
11º Princípio — A escola deve ser o espaço de trabalhar o sistema legal de medidas, pois é,
por excelência, espaço de socialização e de compreensão das relações estabelecidas na
sociedade.
12º Princípio — Este último princípio deve direcionar não só o estudo de decimais, como de
qualquer outro conteúdo e de qualquer área do conhecimento. A escola deve estar atenta à
capacidade do estudante de criar situações-problema e propor soluções para os impasses e
conflitos gerados por estas situações vinculadas à sua vida cotidiana.
MUNIZ, C.A.; BATISTA, C.O.; SILVA, E.B. Matemática e Cultura: Decimais, Medidas e Sistema Monetário. Brasília:
Universidade de Brasília, 2008.

51. Referências Bibliográficas
PIRES, Célia M.C. Educação Matemática: conversas com professores dos anos
iniciais, São Paulo: ZÉ-Zapt Editora, 2012
.MUNIZ, C.A.; BATISTA, C.O.; SILVA, E.B. Matemática e Cultura: decimais, medidas e
sistema monetário. Brasília: Universidade de Brasília, 2008.
Grandezas e Medidas no Ciclo de Alfabetização, Salto para o Futuro, Ano XXIV,
Boletim 8, Setembro 2014
.Matemática: Ensino Fundamental, Coord. João Bosco P. F. Carvalho, Secretaria de
Educação Básica, Ministério da Educação, Brasília, 2010
PDE: Plano de Desenvolvimento da Educação: Prova Brasil: ensino fundamental:
matrizes de referência, tópicos e descritores. Ministério da Educação, Brasília, SEB,
INEP, 2008.
PRÓXIMO ENCONTRO: G1: 06 / G2: 13 / G3: 14/05 (LÍNGUA PORTUGUESA)